基于Laguerre-Voronoi法的三维开孔泡沫金属模型
2022-09-30吴允兵陈晔聂政威
吴允兵, 陈晔, 聂政威
(南京工业大学机械与动力工程学院, 南京 211816)
泡沫金属是指含有泡沫气孔的特种金属材料,它是一种具有超低密度、高比表面积、高比强度,一般孔隙率在40%~97%的具有多孔特性的泡沫状金属新型材料[1-2]。开孔泡沫金属由于其相互连通的网状结构有着非常大的比表面积,导热性能好,流动阻力相对较低,结构的扰动作用也大大提高了换热效果[3-5]。开孔泡沫金属是强化对流换热的优良载体[6-7],在能源、化工及电子等领域具有广阔的应用前景,故其研究对工程应用具有重要价值。
该研究领域的许多学者提出了建立开孔泡沫金属模型的不同方法,从总体来看主要归纳为三种建模方法。第一种建模方法是利用泡沫的数字化影像或断层影像去重新构建真实的泡沫结构,其中使用较多的方式有X射线断层扫描和磁共振成像,它们以一种非破坏性和非侵入性的方式获得泡沫内部结构[8-9]。第二种方法是采用开尔文泡沫空间模型,开尔文晶胞结构也称之为十四面体,由十四个面(八个六边形面和六个四边形面)和二十四个顶点组成[10-11]。这种方法构建的是理想的周期性泡沫结构,且开尔文模型表现出一些特殊的力学性能,其还未从真实材料中得到证实。当前已经有一些研究人员声称开尔文模型不能真实呈现泡沫内部结构,因为其缺乏随机性而不能真正表现泡沫的某些力学性能[10]。
为了得到随机无规律的泡沫结构,许多研究者采用不同的方法来达到真实泡沫的随机性,第三种泡沫金属结构建模的方法随之出现。目前大多数研究者通过Voronoi空间划分法、Laguerre-Voronoi空间划分法和Poisson-Voronoi空间划分法生成泡沫随机结构模型[12-13]。在这种建模方法中,需要在空间中随机设定某些点,通过定义该点最邻近的空间生成泡沫单孔,这种泡沫结构的随机性受到设定点空间分布的强烈影响。然而,通过Voronoi空间划分法产生的泡沫结构每个顶点的支柱数量高于真实泡沫结构的支柱数量,通过Poisson-Voronoi空间划分法产生的泡沫结构参数也与实际泡沫不同[14-15]。Wejrzanowski等[15]提出了使用Laguerre-Voronoi空间划分法建立开孔泡沫金属模型,将所建模型的孔隙率和表面积与实验数据进行对比并修正,结果表明该模型比另外两种模型更加贴合实际泡沫内部结构。
为了很好地呈现开孔泡沫金属内部结构,现基于Laguerre-Voronoi法对封闭空间内随机堆积的球体进行空间划分来建立开孔泡沫金属三维模型,分析变异系数对泡沫孔隙分布的影响,并与商用开孔泡沫金属进行对比验证。
1 模型的建立与方法
1.1 Laguerre-Voronoi空间划分法
Laguerre-Voronoi空间划分法是一种基于加权的Voronoi空间划分方法[13]。对于集合S中的任意一点pi,加权数ri组成一个集合r={r1,r2,…,rn},则集合S中任意点pi和其他任意点q之间的距离表达式为
dL(pi,q)={[dV(pi,q)]2-ri2}1/2
(1)
式(1)中:dL表示Laguerre几何中两点间的距离;dV表示两点间的欧氏距离。
则点pi所对应的单个划分空间表达式为
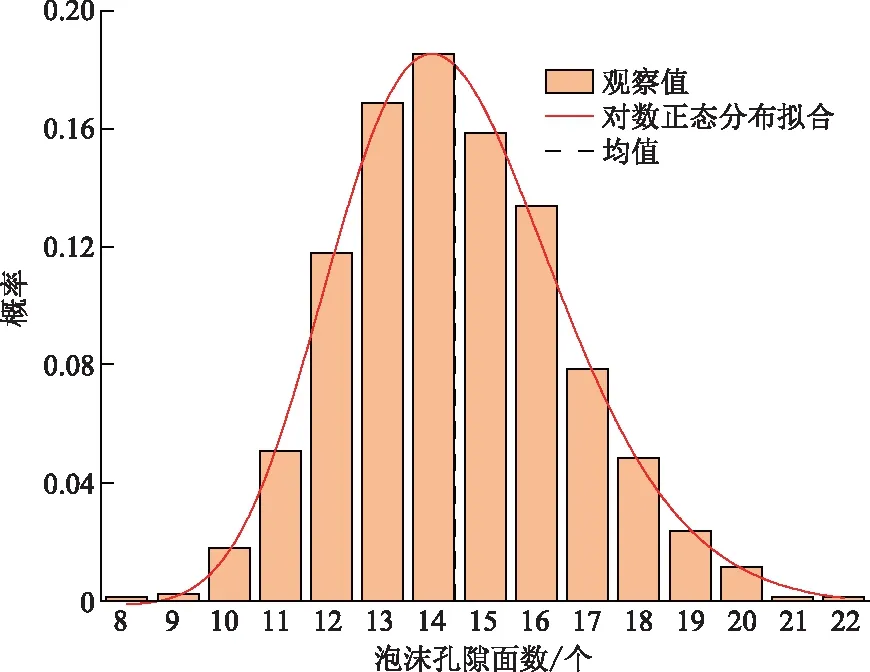
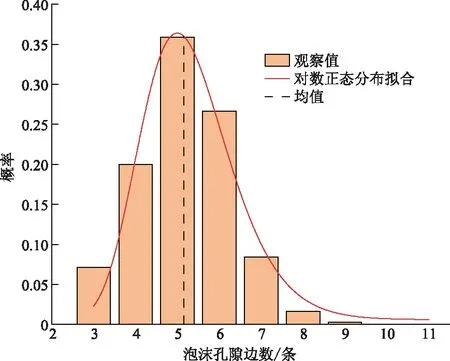
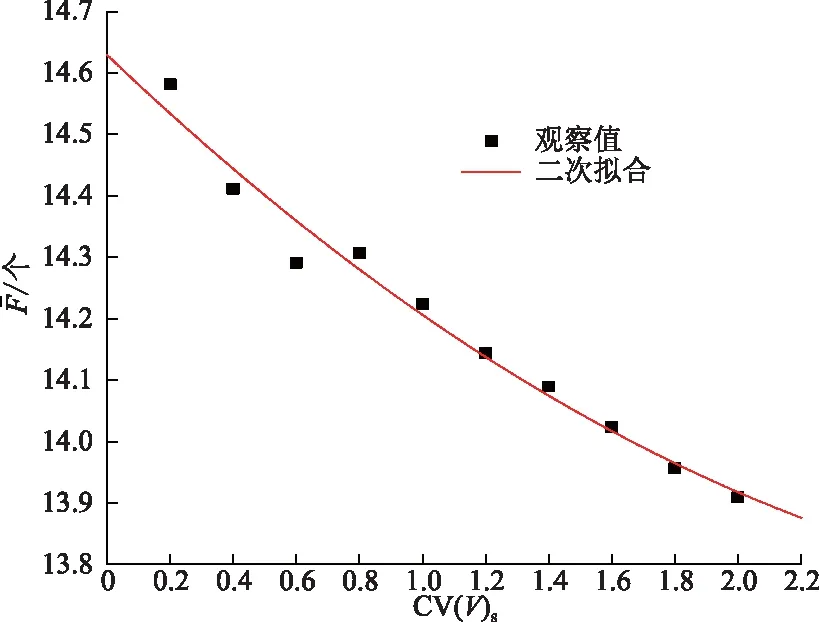
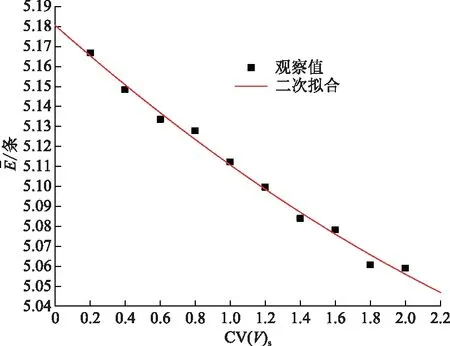
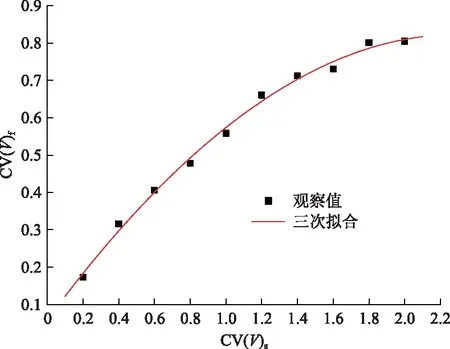
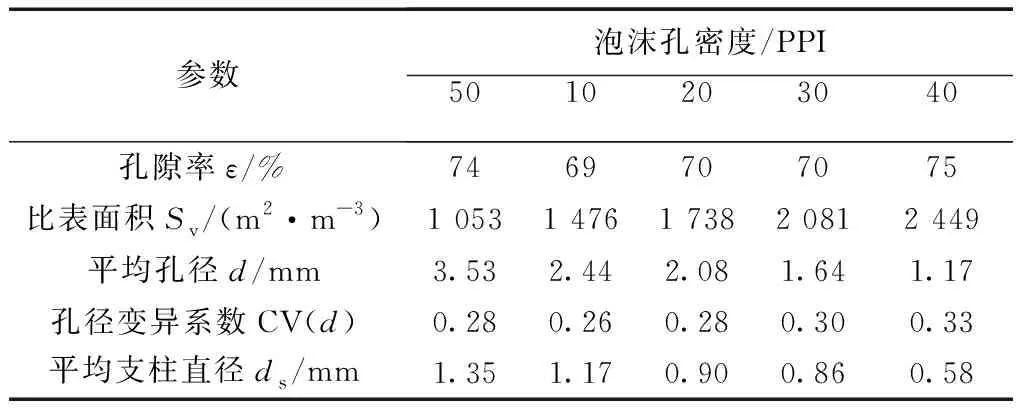
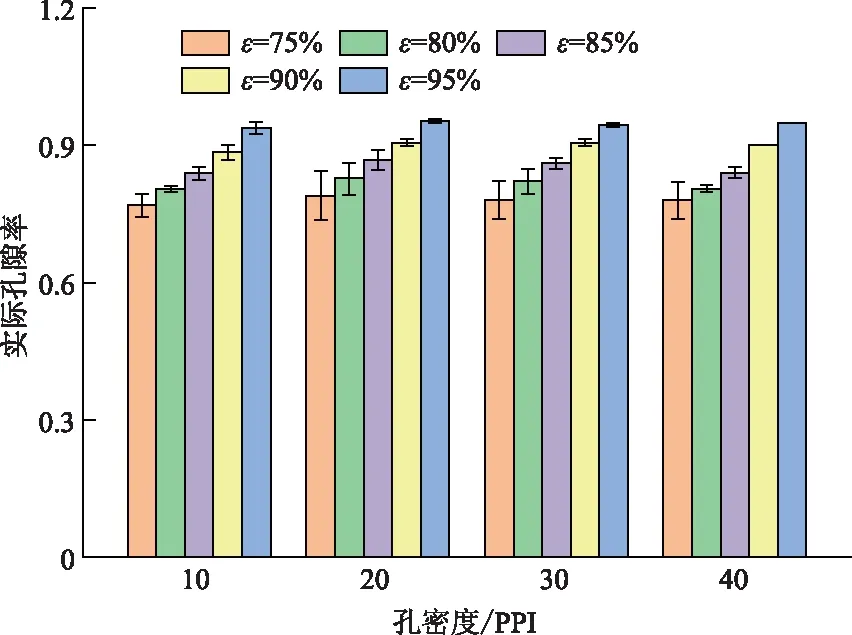
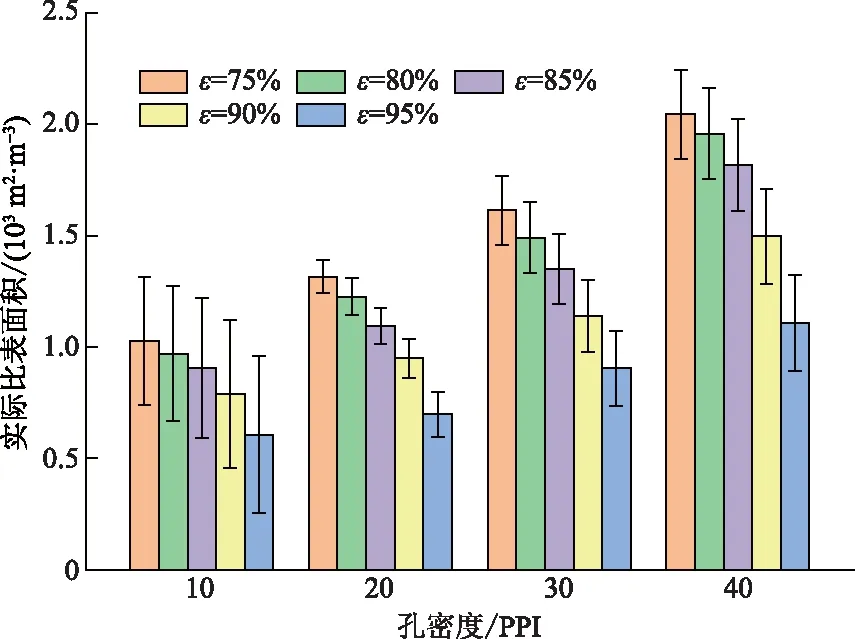
vL(pi)={p|p∈R3,dL(p,pi) (2) 则所有划分空间的表达式为 VL(S,r)={vL(p1),vL(p2),…,vL(pn)} (3) 因此,在空间划分后所呈现的图形被称为Laguerre-Voronoi图,如图1所示。 图1 二维Laguerre-Voronoi图Fig.1 2D Laguerre-Voronoi diagram 提供所有堆积球体中心坐标所组成的集合S以及相应球体半径的集合r,采用Laguerre-Voronoi空间划分法划分固定空间内随机堆积的球体得到Laguerre-Voronoi图,其空间划分方法如图2所示。 在Laguerre-Voronoi图中,每个球体都被相对应的划分空间单独包围着,相邻的划分空间则包围着相邻的球体,两个相切球面的相切平面就是相应多面体的共享面。因此,划分的空间体积分布受到初始球体体积分布的强烈影响。为了提高计算效率,采用APDL语言编写的程序脚本运行,其中随机堆积球体的三维Laguerre-Voronoi图如图3所示。 图2 Laguerre-Voronoi法空间划分规则Fig.2 Space division rules of Laguerre-Voronoi method 由于实际泡沫制造工艺中存在随机性和不完整性,泡沫的孔隙体积变异系数一般在1.09~2.03,实际泡沫孔隙体积分布呈现对数正态分布[16]。因此,需要控制固定空间内随机堆积的球体分布具有一定的对数正态分布。 图3 基于随机堆积球体的三维Laguerre-Voronoi图Fig.3 3D Laguerre-Voronoi diagram based on randomly stacked spheres 本文所进行的开孔泡沫结构建模主要包括以下五个步骤。 (1)利用MATLAB软件编写程序生成具有规定尺寸分布的球体,在程序中设置预先设定的球体体积变异系数CV(V)和平均体积E(V)。 (2)利用LAMMPS软件运行固定立方体空间内随机堆积该组球体的程序脚本。 (3)在APDL中通过运行程序脚本,利用Laguerre-Voronoi空间划分法划分该组随机堆积球体模型,获得相应的三维Laguerre-Voronoi图。 (4)删除步骤(3)中三维Laguerre-Voronoi图的堆积球体、每个球体对应的划分空间内部体积和各空间之间的界面,仅保留各球体划分空间的棱边和顶点。 (5)将步骤(4)生成的模型文件导入ANSYS中,将保留的边缘进行圆柱化以生成金属骨架材料;为减少边界效应并提高计算效率,在SolidWorks软件中进行模型切割,获得开孔泡沫金属三维模型。 基于以上五个步骤给出开孔泡沫建模步骤示意图如图4所示。 对数正态分布是许多工程材料结构的特征代表。因此,研究采用对数正态分布来分析泡沫结构的系列数据。对数正态分布的概率密度函数表达式为 (4) 式(4)中:μ和σ分别为变量对数的平均值和标准差,期望值E(x)和方差Var(x)由μ和σ两个参数构成,表达式为 E(x)=e[μ+(σ2/2)] (5) Var(x)=(eσ2-1)e2μ+σ2 (6) 变异系数CV(x)由标准差SD(x)和期望值E(x)构成表表达式为 图4 开孔泡沫金属三维建模流程示意图Fig.4 Schematic diagram of 3D modeling process for open cell metal foams (7) 式(7)中:SD(x)=Var(x)1/2。 图5~图7分别呈现的是基于孔密度为20 PPI(pores per linearinch)、球体体积变异系数CV(V)=0.4的对数正态分布下随机堆积球体所形成的泡沫孔隙体积、面数和边数分布直方图以及采用相应参数拟合对数正态分布。 图5 泡沫孔隙体积直方图和相应参数拟合的对数正态分布Fig.5 Histogram of foam pore volumes and lognormal distribution of corresponding parameter fitting 图6 每个泡沫孔隙(多面体)面数直方图和 相应参数拟合的对数正态分布Fig.6 Histogram of face number per foam pore(polyhedron) and lognormal distribution of corresponding parameter fitting 图7 泡沫孔隙每个面的边数直方图和 相应参数拟合的对数正态分布Fig.7 Histogram of edge number of per surface of foam pore and lognormal distribution of corresponding parameter fitting 14.629 8,σ= 0.032 5 (8) 5.180 6,σ= 0.003 2 (9) 标准残差对于CV(V)f和CV(V)s之间的关系采用三次拟合,得到表达式为 CV(V)f=-0.003 4[CV(V)s]3-0.129 5× [CV(V)s]2+0.648 0CV(V)s+ 0.058 8,σ= 0.014 8 (10) 式中:σ为标准残差。从图8~图10可以看出,当随机堆积球体的球体体积变异系数以0.2为间隔从0.2递增到2.0时,泡沫结构中每个孔隙的平均面数从14.58递减到13.91,泡沫结构中每个面的平均边数从5.17递减到5.06,但泡沫结构中孔隙体积变异系数从0.17递增到0.80。图10也验证了可以通过改变随机堆积球体的球体尺寸参数来控制泡沫结构中孔隙尺寸的变化。 本文模型的验证是基于Wejrzanowski等[15]所做的工作,其中提出泡沫结构的支柱形状是一个重要的几何特征。大多数已有研究都将Laguerre-Voronoi图中划分空间的边缘简化成直径不变的圆柱体,在一些前者的研究中模型支柱的顶点重叠被忽略不计,未进行相关的误差评估。为了更好地分析泡沫结构,用泡沫孔隙直径d代替泡沫孔隙体积V,两者的关系表达式为 (11) 图8 泡沫结构中每个孔隙的平均面数与相应 随机堆积球体的球体体积变异系数的关系Fig.8 The relationship between average number of faces per pore in foam structure and sphere volume variation coefficient of corresponding randomly stacked sphere 图9 泡沫结构中每个面的平均边数与相应 随机堆积球体的球体体积变异系数的关系Fig.9 The relationship between average number of edges per face in foam structure and sphere volume variation coefficient of corresponding randomly stacked sphere 图10 泡沫结构中孔隙体积变异系数与相应 随机堆积球体的球体体积变异系数的关系Fig.10 The relationship between variation coefficient of pore volume in foam structure and sphere volume variation coefficient of corresponding randomly stacked sphere Wejrzanowski等[15]提出了一种顶点重叠的校正方法,引用其校正的泡沫孔隙率和比表面积表达式为 (12) Sv=[7.38e-1.35CV(d)E(d)-2πds]- (13) 式中:CV(d)为孔径的变异系数;E(d)为平均孔径,mm;ds为泡沫骨架支柱直径,mm。 采用不同孔密度的商业氧化铝泡沫对这里提出的模型进行验证,文献[15]中对典型样本进行三维X射线断层扫描来评估泡沫结构特性,然后采用图像分析法对结构参数进行测量,结果如表1所示。 参考表1中平均孔径E(d)和孔径变异系数CV(d)来控制球体体积对数正态分布进而改变泡沫的孔密度,采用式(12)对泡沫孔隙率进行改变,得到不同孔密度(10、20、30、40 PPI)和不同孔隙率(75%、80%、85%、90%、95%)的三维开孔泡沫金属结构。在不同孔密度以及不同孔隙率条件下,对理论孔隙率与实际孔隙率进行误差分析(图11),总体来看,相对误差均小于±5%。同时作理论比表面积和实际比表面积误差分析(图12)图,对于孔密度为10 PPI且不同孔隙率下的开孔泡沫金属模型,相对误差较大(28%~35%),这是由于在SolidWorks软件中模型的切割具有随机性所造成的,但是其余泡沫金属模型相对误差均小于20%。 图13(a)是本文所建立的孔密度为20 PPI泡沫三维模型,泡沫骨架结构是直径不变的圆柱体,截面形状为圆形;图13(b)是基于本文所建立的模型进行3D打印的开孔泡沫,使用的材料是铸造铝合金AlSi10Mg;图13(c)是从市面上购买的由电沉积法制造的孔密度为20 PPI的泡沫铜,从图13中可以看出泡沫骨架截面形状为凹三角形。因此,本文建立的三维开孔泡沫金属模型存在一定的误差,但是可以很好地呈现实际泡沫的内部结构。 表1 三维X射线断层扫描的泡沫结构Table 1 Foam structure of 3D X ray tomography 图11 实际孔隙率误差分析Fig.11 Error analysis of actual porosities 图12 实际比表面积误差分析Fig.12 Error analysis of actual specific surface areas 图13 泡沫结构误差分析Fig.13 Error analysis of foam structure (2)通过与理论结构参数对比分析,整体来看泡沫孔隙率的相对误差小于±5%,比表面积的相对误差普遍小于20%;对商用开孔泡沫金属进行电镜扫描分析,显示本文所建立的模型存在一定的误差,但是该开孔泡沫金属建模方法可以很好地呈现实际泡沫内部结构,可以为泡沫结构的研究提供一定的参考。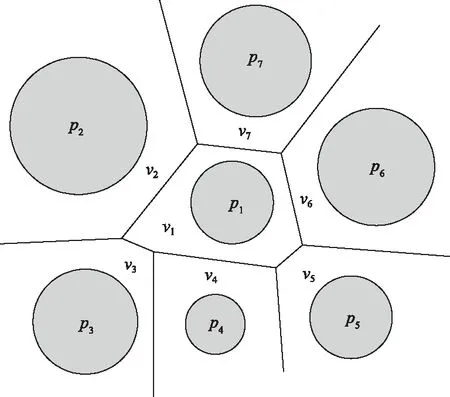
1.2 基于随机堆积球体的Laguerre-Voronoi空间划分法
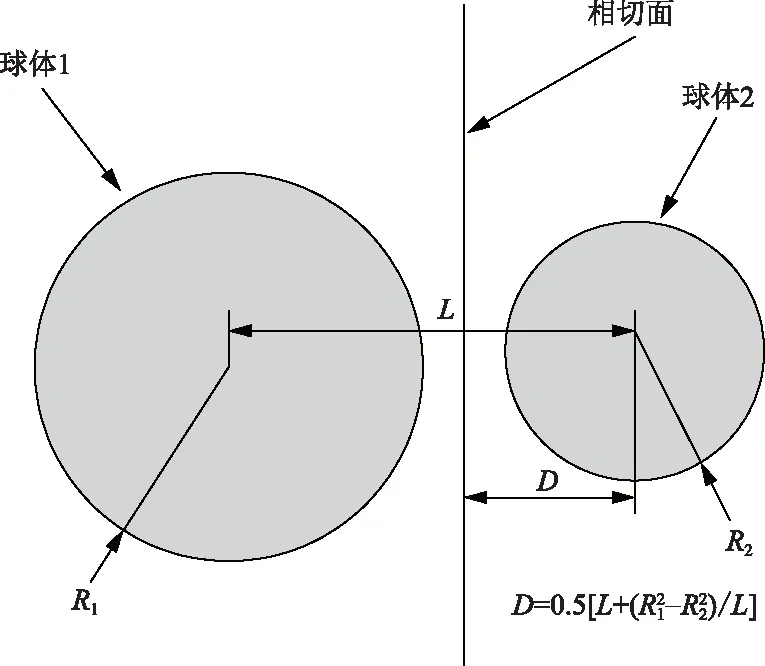
1.3 建模过程
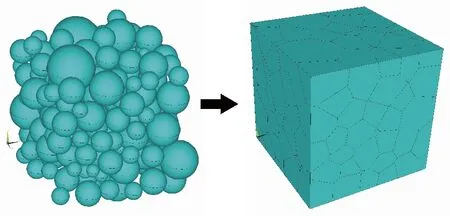
2 结果与讨论
2.1 泡沫孔隙的体积、面和边数分布
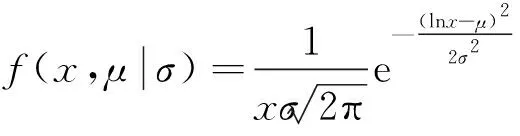

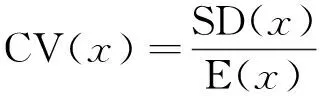
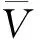

2.2 泡沫孔隙不均匀性影响
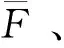
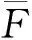
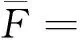
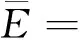
2.3 分析验证



3 结论