函数型空间自回归模型的贝叶斯估计
2022-09-29徐登可田瑞琴
徐登可,田瑞琴
(1.杭州电子科技大学经济学院,浙江杭州 310018;2.杭州师范大学数学学院,浙江杭州 311121)
§1 引言
在当今大数据时代,随着信息化技术的飞速发展,收集数据和储存数据的技术得到了快速的提高;并且随着使用工具越来越先进,人们收集到的数据也越来越复杂.在计量经济学,气象学,医学等方面,常常会获得带有明显函数特性的数据,即观测数据是在空间或时间上的一个或多个维度上获得的,这一类型的数据称之为函数型数据.函数型数据分析已经成为统计学家研究的热点领域之一.目前有很多专家对函数型数据模型进行了参数估计,变量选择,模型检验等比较系统的研究.例如,基于函数型主成分分析,Hall和Horowitz(2007)[1]提出了具有标量响应变量和函数型解释变量的函数型线性回归模型的最小二乘方法,并且证明了获得的估计量具有非参数的最优收敛速度.Shin(2009)[2]提出了部分函数型线性回归模型,并研究了模型中未知回归系数的理论性质.Feng等(2021)[3]研究了函数型单指标变系数模型的参数估计,并且在一定的正则条件下建立了获得估计量的良好理论性质.Zhou和Peng(2020)[4]研究了缺失数据下部分函数型线性回归模型的参数估计.Hu 等(2020)[5]研究了偏正态数据下函数型线性回归模型的异方差检验和参数估计问题.Shi等(2021)[6]研究了函数型分位数回归模型的模型检验问题.另外,有关函数型数据分析的其它研究内容还可以参见文献[7-9].在以上这些文献研究中,函数型数据分析的响应变量是一个独立变量,不是一个具有空间相关的响应变量.然而在实际应用中会发现,在函数型数据建模分析时不仅会存在函数型解释变量,有时还会同时出现具有空间相依关系的响应变量的情形.
目前研究具有空间相依关系的最主要模型是空间自回归模型.空间自回归模型广泛应用于经济学,环境科学以及地理信息等领域,且得到了大量的统计学家和计量经济学家进行深入的研究.例如,Liu等(2018)[10]基于惩罚拟极大似然估计方法研究了空间自回归模型的变量选择问题.Jin和Lee(2019)[11]考虑了空间自回归模型的广义经验似然估计和检验问题.王周伟等(2019)[12]基于Spatial AIC准则研究空间自回归模型的变量选择.Xie等(2020)[13]研究了发散维时空间自回归模型的变量选择,并证明了变量选择方法具有相合性和Oracle性质.Cheng和Chen(2021)[14]提出了部分线性单指标空间自回归模型并且针对模型研究了截面极大似然估计问题.Hu 等(2020)[15]基于函数型主成分分析研究了函数型空间自回归模型的估计,并建立了参数部分和函数系数部分估计的理论性质.
另外近年来由于计算机的快速发展,贝叶斯统计发展非常迅速,取得了非常丰硕的研究成果.例如,Li等(2014)[16]研究了基于似然比检验统计量的贝叶斯版本假设检验.Tang等(2018)[17]基于P样条对线性混合效应变换模型进行贝叶斯估计和贝叶斯局部影响分析.Tian和Song(2020)[18]基于贝叶斯桥惩罚分位数回归研究了模型的贝叶斯变量选择问题.田瑞琴等(2021)[19]研究了纵向数据下半参数均值方差模型的贝叶斯分析.Zhang等(2021)[20]基于分位数回归研究了半参数混合效应双重回归模型的贝叶斯估计问题.但是有关部分函数型空间自回归模型的贝叶斯统计推断成果却几乎没有.因此本文主要基于函数型主成分分析,应用联合Gibbs抽样和Metropolis-Hastings算法相结合的混合算法来研究函数型空间自回归模型的贝叶斯估计.
本文结构安排如下:§2介绍函数型空间自回归模型,函数型主成分分析以及给出基于模型得到的似然函数;§3详细给出实现贝叶斯估计的先验分布,条件分布以及算法;§4节通过大量的模拟研究说明模型与方法的可行性;§5是应用提出的模型和贝叶斯方法对加拿大气温数据进行实证分析;§6是结论.
§2 模型与似然函数
2.1 函数型空间自回归模型
考虑部分线性函数型空间自回归模型

其中Yi表示第i个个体的实值响应变量,Zi表示p维标量型解释变量向量;Xi(t)∈L2(T)为函数型解释变量,L2(T)表示所有定义在T上的平方可积函数构成的希尔伯特空间,不失一般性假设T=[0,1];wij为非随机空间权重矩阵W的第(i,j)个元素,并且满足当i=j时,wij=0;ρ为未知的空间邻近效应参数,θ=(θ1,θ2,···,θp)T是未知p维回归参数,β(t)是定义在[0,1]上的平方可积函数;另外在这里假设εi是独立同分布服从于均值为零,方差为σ2的正态分布,即εi~N(0,σ2).
模型(1)也可以写成矩阵的形式,令Y=(Y1,Y2,···,Yn)T,Z=(Z1,Z2,···,Zn)T,X(t)=(X1(t),X2(t),···,Xn(t))T,ε=(ε1,ε2,···,εn)T.那么模型(1)可以重新被写成

2.2 似然函数
首先,定义函数型变量X(t)的协方差函数和经验协方差函数分别为
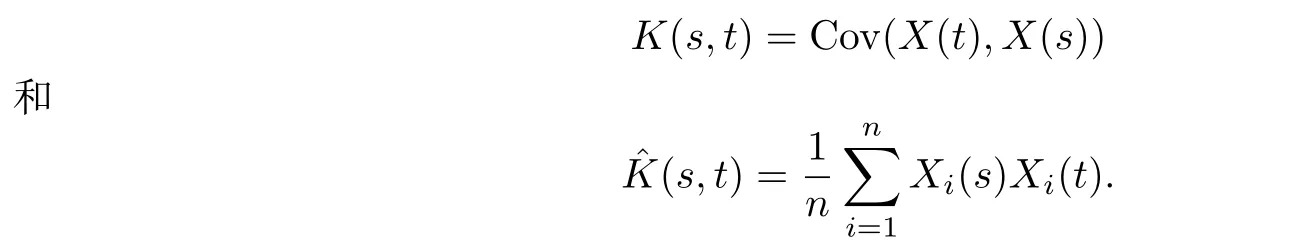
在这假设协方差函数对应的特征根从大到小排列为λ1>λ2>··· >0,对应的经验协方差函数特征根为,{φj}和分别为对应的正交特征向量.显然这里{φj}和为空间L2([0,1])上的标准正交基,那么利用Mercer定理可得K(s,t)和(s,t)分别有谱分解

其中ξi是不相关的随机变量,且满足,和γi=〈β,φi〉,这里〈·,·〉表示在L2(T)内上的内积.因此把(3)代入模型(2)可得

其中m ≤n表示截断参数.若用近似φj,模型(5)可以被重新写成

其中e=AY -Zθ-Uγ,A=In-ρW,和In是n×n维单位阵.
§3 贝叶斯估计
3.1 先验分布
为了应用贝叶斯方法估计模型(1)中的未知参数,需要具体化未知参数的先验分布.类似于Ju等(2018)[21],为了简便在这假设θ和γ相互独立且具有正态先验分布,分别为θ~N(θ0,Σθ)和γ~N(γ0,Σγ),其中假设超参数θ0,γ0和Σθ,Σγ是已知的.另外假设ρ~U(-1,1),σ2~IG(c0,d0),其中c0和d0是已知的超参数,“U(·,·)”表示均匀分布,“IG”表示逆Gamma分布.这样未知参数的联合先验定义为

其中“p(·)”表示参数的先验概率密度函数.
3.2 贝叶斯后验推断
令Ψ=(θ,γ,ρ,σ2),在这里主要利用MCMC方法获得未知参数Ψ的贝叶斯估计.基于似然函数(7)和联合先验分布(8)可以获得参数Ψ的联合后验分布,具体为

基于上式进行直接抽样和后验推断是比较困难的.为了解决这个问题,首先需要推导获得每一个未知参数的条件分布,然后利用Gibbs抽样和Metropolis-Hastings 抽样算法相结合的混合MCMC抽样算法来从各自的条件分布中抽样,具体如下.
·θ的条件分布

·γ的条件分布

·σ2的条件分布

·ρ的条件分布

那么这样就可以通过表1中的具体MCMC算法产生后验样本序列(θ(l),γ(l),ρ(l),σ2(l)),l=1,···,J.从(10)-(12)表达式中很容易发现,这些条件分布是熟悉的正态分布和逆Gamma分布,那么从这些分布抽取随机数是比较容易的.但是条件分布p(ρ|Y,Z,X,θ,γ,σ2)是不熟悉且相当复杂的分布,如何从这个分布中抽取随机数是比较困难.这样,选择Metropolis-Hastings算法来从这个分布中抽取随机数.并选择正态分布作为建议分布[21],其中通过选择来使得接受概率在0.25与0.45之间.算法具体应用如下: 在(l+1)次迭代时且目前值为ρ(l),从建议分布产生一个新的备选值ρ*,它被接受的概率为

表1 未知参数Ψ=(θ,γ,ρ,σ2)的后验样本抽样算法

这样基于以上MCMC算法就可以收集到收敛的后验样本并记收集到的MCMC样本为Ψ(k)=(θ(k),γ(k),ρ(k),σ2(k)),k=1,···,M,M <J.这样参数的后验均值估计分别可以估计为


§4 模拟研究
本节通过数值模拟研究来说明前面提出的贝叶斯估计方法的有效性.数据从模型(2)产生,其中θ=(1,-0.5,0.5),Z产生于多元正态分布N(0,ΣZ),(ΣZ)i,j=0.5|i-j|,i,j,=1,2,3.为了比较不同的信噪比影响,选取模型方差σ2=0.25和1.另外令空间参数ρ=0.5,0,-0.5表示不同程度与方向的空间依赖性.类似于Lee(2004)[22],设置权重函数W=IR ⊗Hq,Hq=,其中lq表示全是1的q维向量,“⊗”表示Kronecker积,n=R×q.针对函数型部分,类似于Shin(2009)[2],函数型系数其中ξj独立同分布于均值为0,方差为λj=((j-0.5)π)-2的正态分布,在这个模拟中,考虑未知参数θ,γ,ρ,σ2的无信息先验:θ0=03,Σθ=10×I3,γ0=0m,Σγ=10×Im,c0=d0=0.01,其中0m表示全是0的m维向量.进一步选择R=50,70和q=3,6.这里通过使用函数型主成分分析方法获得最优的截断参数m,即
在上面的各种设置环境下,应用联合Gibbs抽样和Metropolis-Hastings算法的混合MCMC算法来计算未知参数的贝叶斯估计.对于每一种情形重复计算100次.对于每次重复产生的每一次数据集,MCMC算法的收敛性可以通过EPSR值来检验[23],并且在每次运行中观测得到在3000次迭代以后EPSR值都小于1.2且接近于1.因此在每次重复计算中丢掉前3000次迭代以后再收集M=2000个样本来产生贝叶斯估计.所有的结果展示在表2-4中.另外,为了测量函数型系数估计的好坏,选择用如下定义的RASE来衡量精确度

表2 当ρ=0.5时不同情况下未知参数的贝叶斯估计结果

表3 当ρ=0时不同情况下未知参数的贝叶斯估计结果


表4 当ρ=-0.5时不同情况下未知参数的贝叶斯估计结果
其中ts,s=1,···,N表示函数型系数计算的格子点,N=200.模拟结果展示在表5中.为了更加直接的看出函数型系数估计的好坏,画出并展示了一部分曲线估计图在图1-图6中.

图1 当ρ=0.5时, σ2=1,R=50,q=3和σ2=1,R=70,q=3的函数型系数β(t)的贝叶斯估计结果

图2 当ρ=0.5时, σ2=1,R=50,q=6和σ2=1,R=70,q=6的函数型系数β(t)的贝叶斯估计结果

图3 当ρ=0.5时, σ2=0.25,R=50,q=3和σ2=0.25,R=70,q=3的函数型系数β(t)的贝叶斯估计结果

图4 当ρ=0.5时, σ2=0.25,R=50,q=6和σ2=0.25,R=70,q=6的函数型系数β(t)的贝叶斯估计结果

图5 当ρ=0时, σ2=1,R=50,q=3和σ2=1,R=70,q=3的函数型系数β(t)的贝叶斯估计结果

图6 当ρ=-0.5时, σ2=1,R=50,q=3和σ2=1,R=70,q=3的函数型系数β(t)的贝叶斯估计结果
在表2-表4中,“Bias”表示基于100次重复计算未知参数的贝叶斯估计和真值之间的偏差,“SD”表示未知参数贝叶斯估计的标准差.从表2-表5中可以得到以下结论(i)在估计的偏差Bias和SD值方面,不管何种情形下贝叶斯估计都相当精确.并且随着样本量的增大,模型中参数部分和函数型系数部分的贝叶斯估计结果变得越来越好.(ii)基于不同的空间参数ρ,贝叶斯估计结果都是一样的好.(iii)当模型方差逐渐变小时,贝叶斯估计效果也变得越来越好.(iv)随着样本量的增大,RASE值变得越来越小,这也表明函数型系数估计得越来越好.从图1-图6中也展示了不管何种情形下,估计出来的函数型系数的曲线与相应的真实函数的曲线逼近得都比较好,这与表5展示出来的结果是一样的.总之,从以上所有结果中可以看出应用提出的贝叶斯估计方法能很好地恢复函数型空间自回归模型中的真实信息.

表5 不同情况下函数型系数β(t)的贝叶斯估计结果(RASE值)
另外,为了测试提出的贝叶斯估计方法在协变量高维情况下的效果,令θ=0.5×1K,K=15,“1K”表示全是1的K维向量.其它参数的设置和前面一样.为了节省空间,在这里仅列出σ2=0.25,R=70,q=3情况下的模拟结果并展示在表6中,表中“Biasθ” 表示所有θ分量估计的偏差绝对值的和,“SDθ” 表示所有θ分量估计的标准差的和;“Biasσ2”,“Biasρ”,“SDσ2”,“SDρ”表示相应参数的绝对偏差和标准差;“RASEβ”表示函数型系数β估计的RASE值.从表6中不难发现,在不同的空间参数下,所有参数的估计效果差别不大且是比较满意的.这说明所提出的贝叶斯估计方法在高维情况下运行是可行有效的.

表6 当R=70,q=3,σ2=0.25时高维协变量情况下所有参数的贝叶斯估计结果
§5 实际数据分析
本节利用前面提出的函数型空间自回归模型与贝叶斯方法来分析加拿大气温数据,有关数据描述可以参见R语言包fda中CanadianWeather的介绍.该数据由加拿大35 个气象站1960年到1994年期间每天的平均降雨量,平均气温以及气象站所处的经纬度等信息数据组成.为了分析年降雨量和气温之间的关系,假设35个气象站的年平均降雨总量的对数为Y,35 个气象站的每天平均气温曲线为X(t).在这里首先用如下定义的莫兰指数计算空间相关性,

其中n=35,wij是空间权重值,即空间权重矩阵W的元素;S0是所有空间权重的聚合,即S0=在这个实证分析中,首先利用35个气象站的经纬度数据计算它们各自的欧氏距离,然后用欧氏距离的倒数以及进行标准化生成空间权重矩阵W.在此基础上计算出莫兰指数为0.2655和显著性检验p值为0.000,因此可以认为35个气象站的年降雨量存在空间相关性,有理由认为存在空间效应.故为了分析每天平均气温对年平均降雨量的影响,采用以下的函数型空间自回归模型进行分析,

通过应用文中提出的贝叶斯估计方法和无信息先验获得空间参数的估计为=1.184以及函数型系数β(t)的曲线估计和95%的置信带估计如图7所示.其中为了测试算法的收敛性,画出了所有未知参数的EPSR值的图,且列在图8中,从图8中也能看出3000次迭代以后所有参数的EPSR值都小于1.2,这表示3000次迭代以后算法都收敛了.

图7 实例分析中函数型系数β(t)的贝叶斯估计(实线);以及95%的置信带估计曲线(虚线)

图8 实际数据分析中所有参数的EPSR值
最后再次对残差数据计算获得莫兰指数为-0.054和显著性检验p值为0.449,因此可以认为使用该空间模型有效提取了信息和模型拟合效果还是比较不错的.
§6 结论
针对响应变量具有空间效应的部分函数型空间自回归模型,应用基于Gibbs抽样和Metropolis-Hastings算法相结合的混合MCMC算法,以及运用Karhunen-Lo`eve表示定理来逼近函数型系数的思想研究了模型的贝叶斯估计方法.模拟研究显示(1) 随着样本量的增大,函数型系数和参数部分的贝叶斯估计效果都是越来越好;(2) 在不同的空间参数模拟环境设置下获得的模型贝叶斯估计效果都是一样好;(3) 随着模型方差逐渐变小,模型中参数部分和函数型系数部分估计的效果也都会变得越来越好.另外对加拿大气温数据进行了实证分析,首先计算度量空间相关性的莫兰指数,显示数据具有空间相关性.因此应用提出的函数型空间自回归模型对数据进行了建模和贝叶斯分析,通过混合MCMC算法获得空间参数和函数型系数的估计,最后也进行了残差分析,结果显示该模型拟合数据比较有效.因此通过这些模拟仿真结果和实证分析结果都显示了所提出的模型与贝叶斯方法的有效性和可行性.
