具有分布时滞的毒品滥用防治模型的稳定性分析

刘 风

(中央司法警官学院 信息管理系,河北保定 071000;中央司法警官学院 戒毒康复研究中心,河北保定 071000)

§1 引言

按照《2020年中国毒情形势报告》公布的数据,尽管我国登记在册的吸毒人数已连续三年持续下降,但是截至该年底全国仍有吸毒人员180.1万名,占人口总数的0.13%,我国毒品滥用问题依旧不容乐观.

在公共卫生领域，数学模型一直是研究传染病流行规律的有效工具之一.文献[1-3]通过将海洛因的吸食扩散与传染病的流行进行类比,打开了应用传染病模型研究海洛因吸食问题的大门.针对海洛因成瘾现象,White 和Comiskey[4]利用常微分方程构建了一个仓室传染病模型,计算了模型的基本再生数和平衡点,并对基本再生数进行了敏感性分析,奠定了毒品滥用流行病模型的研究基础.Mulone 和Straughan[5]对文献[4]进行了补充,放松了系统流入率为常数的假设,并证明了正平衡点的全局稳定性.基于文献[4-5],文献[6]将吸毒人员划分为轻度和重度两个人群,建立了甲基苯丙胺流行病模型,分析了模型的动力学性态并进行了模拟仿真.

现实中吸毒者接受治疗后往往又会出现复吸现象,从治疗到复吸,状态的转移通常存在一个时间上的滞后.为了使模型能够更好地刻画现实情况,Liu和Zhang[7]将复吸时滞因素引入White和Comiskey的模型,建立了具有分布时滞的海洛因流行病模型,证明了无毒平衡点的全局稳定性和地方病平衡点的局部稳定性.Huang和Liu[8]进而证明了文献[7]中地方病平衡点的全局稳定性.文献[9-11]则考虑首次吸毒的时滞因素建立了相应的海洛因流行病模型,并研究了模型平衡点的稳定性.

接种疫苗是一种有效控制传染病流行的预防措施.Parsamanesh和Erfanian[12]构建了带有疫苗接种措施的传染病模型,证明了模型平衡点的全局稳定性.Arino等[13]分析了疫苗接种措施对传染病模型稳定性的影响,研究结果表明当疫苗并非完全有效时,模型出现了后向分支现象.

针对毒品易感人群,加强毒品危害的宣传教育,可以起到类似于接种疫苗的预防作用.与上述海洛因流行病模型只考虑治疗措施不同,本文在预防和治疗双重措施基础上引入复吸时滞影响因素,建立了一个具有分布时滞的毒品滥用防治模型,通过分析模型的动力学性态,讨论了影响模型基本再生数的敏感性因素,研究结果为决策部门制定相关公共政策提供了理论依据.

§2 模型构建

毒品滥用人群的演化过程如图1所示.S(t),I(t),T(t)和R(t)分别代表t时刻易感人群,未隔离吸毒人群,隔离治疗人群和免疫人群的人数.Λ是系统补充率.假设免疫人群不再吸毒,隔离治疗人群不具有传染性,β是未隔离吸毒人群与易感人群的有效接触率,采用双线性发生率.θ为针对易感人群进行毒品危害宣传教育的有效率,假定0＜θ ＜1,即宣传教育并非完全有效.μ代表自然死亡率,δ1和δ2分别为未隔离吸毒人群和隔离治疗人群的吸毒致死率,ε是未隔离吸毒人群的社区治疗康复率,p为隔离治疗率,φ是隔离治疗康复率,σ(t,s)表示经过时滞s到达t时刻的复吸人数,根据图1中各状态转移关系得到时滞微分系统

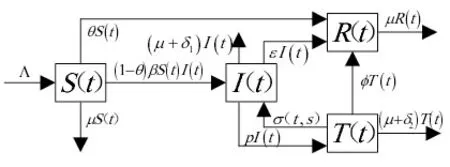
图1 毒品滥用人群的演化过程

考虑到复吸时滞因人而异,设τ是时滞上限,时滞分布参数s ∈[0,τ],f为非负的连续函数,则是时滞s的分布函数.从t-s时刻开始接受治疗,经过时滞s到达时刻t未康复的幸存者为pI(t-s)e-(μ+δ2+φ)s,故t时刻的复吸人数.系统所有参数非负,初始条件为

其中,为将区间[-τ,0]映射到的所有连续函数组成的巴拿赫空间.基于系统解的连续性,T(0)应满足

由系统(1)中的第三个方程和式(3)有

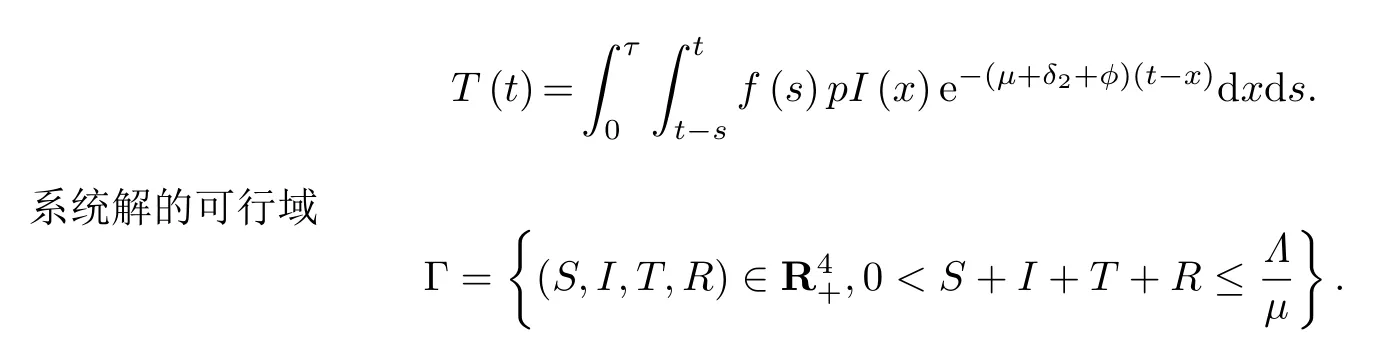
Γ是正不变集,对于∀t ＞0,满足初始条件(2)的解及其ω极限集仍在可行域Γ内,系统(1)是适定的.

由于系统(1)的前三个方程独立于R(t),而T(t)又完全取决于I(t),所以下面主要研究二维系统

§3 平衡点和稳定性

3.1 无毒平衡点及其稳定性

定理3.1系统(4)总是有无毒平衡点E0=S0,I0）,当R0＞1时,E0是不稳定的,当R0＜1时,E0全局渐近稳定.

证系统(4)在E0处的特征方程为[λ+(μ+θ)]g(λ)=0,其中

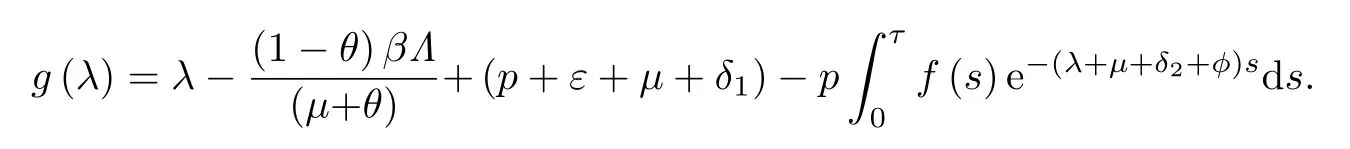
可见λ=-(μ+θ)＜0是一个特征值,其他特征值是方程g(λ)=0的根.

当R0＞1时,由和g(+∞)=+∞,可知方程g(λ)=0至少存在一个正根,所以E0是不稳定的.

当R0＜1时,设g(λ)=0的根λ=a+bi,a,b ∈R.若a ≥0,将λ=a+bi代入方程g(λ)=0,可以推出

与R0＜1矛盾,所以a ＜0,E0是局部渐近稳定的.

为了完整地证明定理3.1,考虑Lyapunov泛函

因为函数v(z)=z-1-lnz,z ∈R+在z=1处取到最小值v(1)=0,所以V(t)≥0,当且仅当在E0处等式成立.下面证明是非正定的.首先计算V1对t的导数

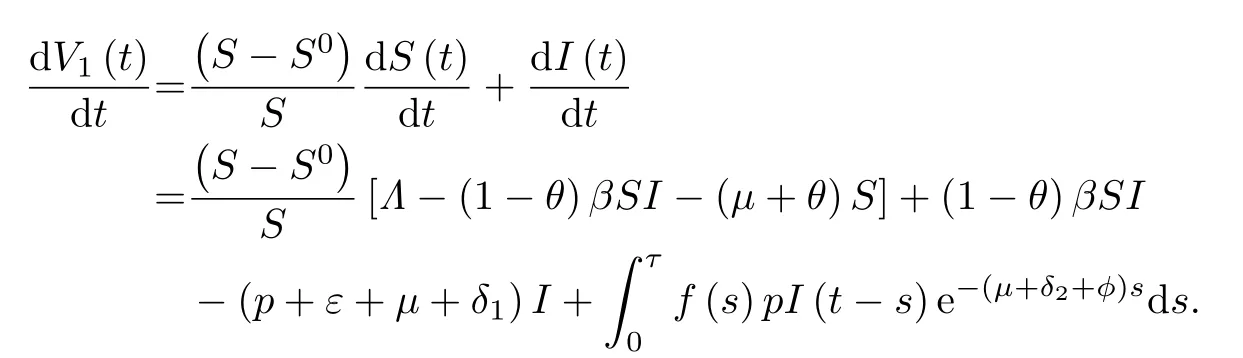
因为Λ=(μ+θ)S0,所以

其次计算V2对t的导数

合并式(5)和式(6)得到

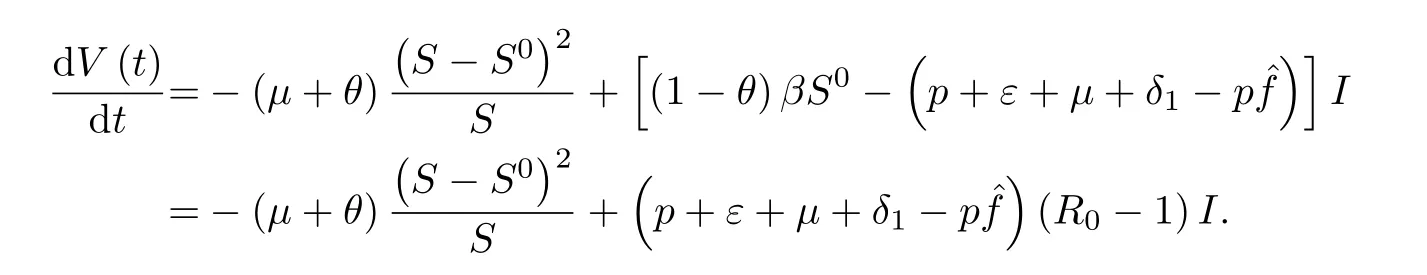
因为R0＜1,所以正定泛函V(t)关于时间t的导数非正定.设M1是的最大不变子集,若要使,则需满足S(t)=S0,I(t)=I0,因此M1=E0,由E0的局部渐近稳定性和LaSalle不变集原理可知E0全局渐近稳定.

3.2 地方病平衡点及其稳定性

R0＞1时,除不稳定的无毒平衡点E0外,系统(4)还有一个地方病平衡点

定理3.2当R0＞1时,系统(4)的地方病平衡点E*是局部渐近稳定的.

证在E*处,系统(4)的特征方程为

由于λ的各项系数和常数项均大于零,故方程(7)的两个根均具有负实部,E*是局部渐近稳定的.可见E*不稳定只能出现在τ＞0,且方程(7)的根从虚轴的左侧穿过虚轴进入到复平面的右半平面时.不失一般性,设λ=wi,w ＞0是方程(7)的一个根,则有分离实部和虚部得到

定理3.3对于系统(4),当R0＞1时,地方病平衡点E*是全局渐近稳定的.

证考虑Lyapunov泛函

显然W(t)≥0,当且仅当在E*处等式成立.下面证明是非正定的.首先计算W1对t的导数

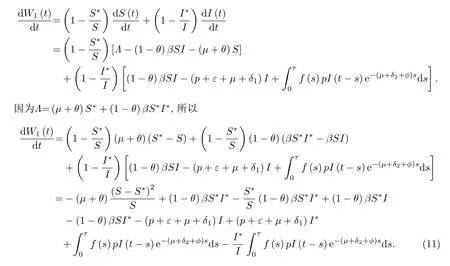
其次计算W2对t的导数

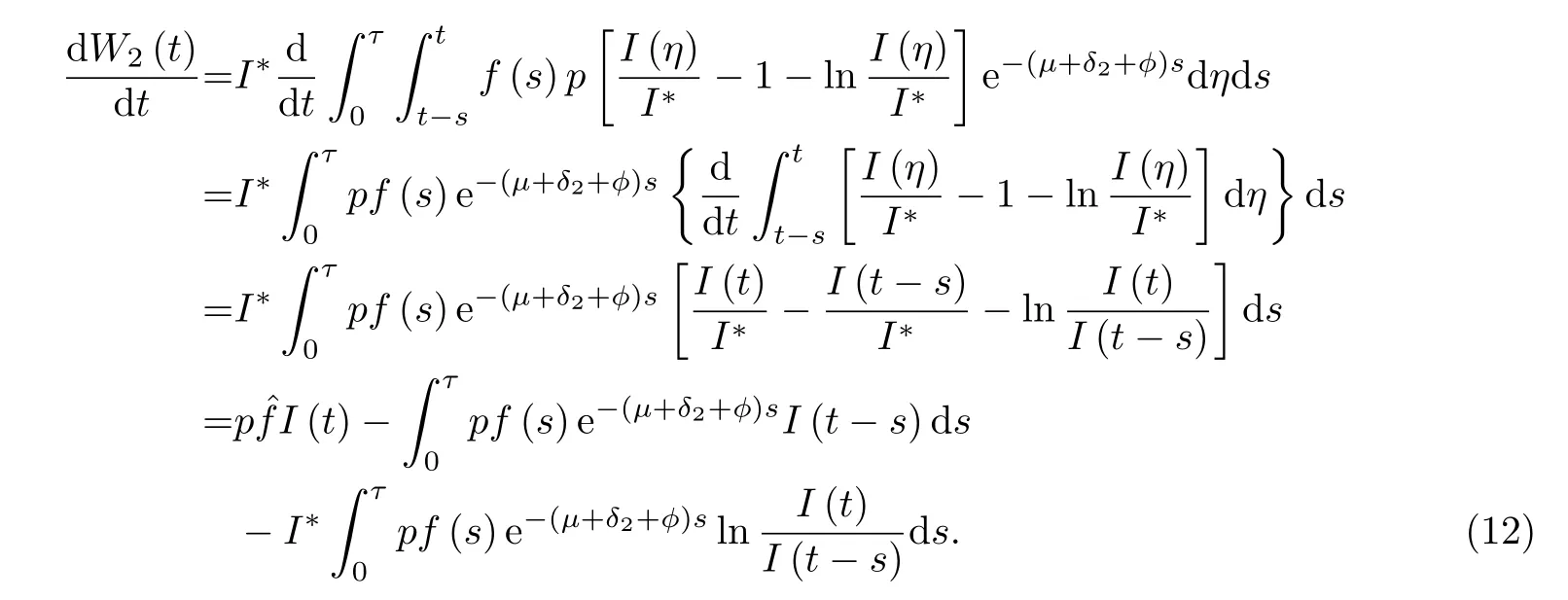
合并式(11)和式(12)得到

§4 数值模拟

以某市相关数据为基础设定参数值

利用MatLab软件模拟不同初始条件下未隔离吸毒人群的演化过程,验证平衡点的存在性和稳定性.简单起见,设.R0=1时,τ ≈1.3035.

首先考虑τ=15,即R0≈0.4173＜1时,如图2(a)所示,无论初始状态如何,未隔离吸毒人群的人数最终都将趋近于0，模拟结果验证了无毒平衡点E0的存在性和全局渐近稳定性.其次当τ=1,β=1.3×10-7,即R0≈1.4207＞1时,如图2(b)所示,对于不同的初始值,未隔离吸毒人群的人数最终都趋近于唯一的正平衡点,模拟结果表明系统唯一的地方病平衡点E*具有全局渐近稳定性.

图2 平衡点模拟结果

由于基本再生数R0是决定毒品滥用是否持续流行的一个关键阈值,因此有必要就R0对其参数进行敏感性分析.下面分别计算R0关于参数β,θ和p的敏感系数.

可以看出R0与β的变化方向是一致的,而与θ和p的变化方向相反,若要使R0＜1,可以通过降低β或者提高θ和p得以实现.显然相对于p,R0对β的变化更为敏感,图3(a)中R0关于β和p的等值线也支持了这个结论.

R0对θ的相对变化率取决于各参数的具体取值,固定Λ=1×104,β=1×10-7,ε=0.005,φ=0.3,μ=δ1=δ2=0.004,设置θ ∈[0.02,0.08],p ∈[0.02,0.08],画出R0关于θ和p的等值线图.如图3(b)所示，此时,R0对θ的变化比对p的变化更为敏感.

图3 R0的等值线图

综合上述分析,相对于p,β和θ是对R0更为敏感的影响因素,这意味着若通过降低R0减小吸毒人员规模,进而消除毒品滥用现象,事前预防比事后治疗是更为有效的措施.

§5 结论

通过引入复吸时滞影响因素,本文建立了一个具有分布时滞的毒品滥用防治模型,在计算模型基本再生数R0的基础上,分析和验证了模型的平衡点及其全局渐近稳定性,并就R0对其参数进行了敏感性分析.当R0＜1时,模型具有全局渐近稳定的无毒平衡点,毒品滥用现象将最终消亡.当R0＞1时,模型具有唯一全局渐近稳定的正平衡点,毒品滥用现象将持续流行.相对于参数p,R0对参数β和θ的变化更为敏感,抑制毒品滥用的流行,事前预防比事后治疗更为有效.这意味着若要根除毒品滥用现象,必须严厉打击制毒贩毒犯罪活动,深入实施毒品预防教育,尤其是青少年毒品预防教育工程,创新完善堵源截流机制.唯有这样,才能不断推动禁毒,戒毒工作高质量发展，为全面落实健康中国战略做出贡献.

今后需要进一步结合现实数据深入研究各参数与仿真结果的定量关系及影响规律,进而将模型用于预测毒品滥用的流行趋势,为决策部门制定更有效的公共政策提供理论依据.