基于有理变换的改进辅助方程法在变系数非线性发展方程中的应用
2022-09-29尹天乐
尹天乐 庞 晶
(1.内蒙古工业大学,理学院,内蒙古呼和浩特 010051;2.内蒙古自治区生命数据统计分析理论与神经网络建模重点实验室,内蒙古呼和浩特 010051)
§1 引言
近年来,随着对孤子理论的研究,学者们逐步建立和构造起来一些以计算机符号为主的求解代数方法,而直接代数法具有应用范围较为广泛,容易实现以及效率较为高的优势.并且,直接代数法又包含了展开法[1-2],双曲函数展开法[3-6],exp(-φ(ξ))展开法[6-7],Jacobi椭圆函数展开法[8-10],辅助方程法[11-14]等,这些方法都具有相似的求解过程,其求解步骤主要分为四步.(在参考文献中均有体现)
1.对给定非线性发展方程进行行波变换,得到常微分方程;
2.引入辅助方程,并根据齐次平衡原则设解;
3.将辅助方程代入到常微分方程中,并且令相关整式的各次幂系数为0,得到一个代数方程组;
4.求解代数方程组,并利用辅助方程的解得到给定非线性发展方程的精确行波解.
为方便表达,将类似于上述求解过程的方法统称为辅助方程法.
各种辅助方程法的主要不同之处是所选择的辅助方程,在展开法中,所选取的辅助方程是二阶线性常微分方程(15);在双曲正切函数展开法中,所选取的辅助方程是(20);在Jacobi椭圆函数展开法中,辅助方程类似于(2),等等.简言之,大多数辅助方程可以分为三类: 二阶常微分方程和广义Riccati方程

其中αi和βi为任意常数.在特定的情况下,通过特定的变换,二阶辅助方程可以与广义Riccati方程或一般椭圆函数方程相互转换,例如,对式(1)做变换可以得到式(15),反之同理.
由于各种辅助方程法所引入的辅助方程不尽相同,那么所设的解也不尽相同,例如在exp(-φ(ξ))展开法中,设解为

其中,ηi(i=1,2,3,···,n)为待定未知量;在双曲正切函数法[6]中,设解为

等等.所以在求解非线性发展方程时,可否仅依据方程的自身得到解? 在广田双线性方法[14-17]中,可以通过有理变换(11)得到一个对数函数形式的解,但是在求解变系数非线性发展方程时会比较困难.
本文总结前人的方法与经验,在处理变系数非线性发展方程时,将传统辅助方程法改进,在做行波变换之前引入有理变换,并通过特定的方式得到给定方程的初步的解,再依据辅助方程等得到变系数非线性发展方程的精确行波解.§2较为详细地说明了本文的方法过程;§3-§5分别用展开法,展开法和椭圆函数展开法的辅助方程求解了一类KdV方程.结果表明,本文所给的方法是适用于多种辅助方程,并且通过有理变换等手段可以求得变系数非线性发展方程的一个相对统一的解.与传统辅助方程法相比较,其优势在于无需依据各种辅助方程法的特性去设解,并且在求解过程中可以省去如设解(3),(4)中出现的ηi等多个待定未知量,这使计算过程更加方便简洁.更重要的是,本文的方法可以将多种辅助方程法的求解过程统一化,进一步完善辅助方程法的研究理论.
§2 方法简介
本节简单说明所给的方法.现引入变系数非线性偏微分方程

其中u=u(x,t)是未知函数.
步骤一 首先作有理变换(11)代入到(5)中,得到由F(x,t)和G(x,t)及它们的各阶微分组成的等式

其中F=F(x,t),G=G(x,t)是未知函数.(一般地,为了简便计算,在作有理变换之前,根据不同方程的不同特点,需要引入u=wx或者u=wxx将方程转化为等价形式)*
步骤二 从(6)中选取两个特定的项Φ和Ψ,令Φ+Ψ=0,可以得到F(x,t)和G(x,t)的关系,然后根据有理变换可以得到方程(5)的解

在这里,Φ和Ψ需要满足如下条件.
1.Φ是由式(5)中最高阶线性项进行有理变换所得到的项,Ψ是由式(5)中最高幂次的非线性项进行有理变换所得到的项.
2.Φ和Ψ均是由F(x,t)和G(x,t)及它们的一阶微分组成的项.
步骤三 做行波变换G(x,t)=G(ξ),其中ξ=kx+ω(t),并且引入辅助方程,例如(15),(25),(32)等.
步骤四 将F(x,t)和G(x,t)的关系,行波变换以及辅助方程带入到(6)后,令关于G(ξ)的整式各次幂的系数为0,则得到以k和ω(t)为未知量的一个线性代数方程组.
步骤五 借助计算机软件Mathematica求解步骤四中得到的代数方程组,以确定相关的待定未知量.然后将F(x,t)和G(x,t)的关系,行波变换以及辅助方程带入到解(7)中,再依据辅助方程的解和代数方程组的解,便可得到方程(5)的精确行波解.
*: 在作有理变换之前引入u=wx或者u=wxx有利于方便计算,§3 KdV方程为例,其原因主要有以下两点理由.
一.由于方程(8)中最高阶的线性项为u3x的阶数是O(u3x)=n+3,最高幂次的非线性项为uux的阶数是O(uux)=2n+1,平衡得到n=2;然而,在方程(10)中平衡得到n=1,所以方程(10)的截断形式级数解要优于方程(8)的.
本文的其它方程同理,读者可自行验证.
§3 改进辅助方程法―展开法在变系数KdV方程中的应用
展开法是王明亮等人于2008年提出的一种构造非线性发展方程精确行波解的方法,其选取的辅助方程为二阶线性微分方程(15).本节应用展开法的辅助方程求解变系数KdV方程

代入到方程(8)后对x进行积分并且取积分常数为0,将其化成等价形式

代入到式(10),整理得到

再根据之前进行的有理变换得到方程(8)的解

然后做行波变换G(x,t)=G(ξ),其中ξ=kx+ω(t),G(ξ)为辅助方程

其中a3为任意非0常数.
最后将行波变换以及辅助方程(15)带入到解(14)中,得到

再根据辅助方程的解(16)和代数方程组的解(18),可以得到如下所示的变系数KdV方程(8)的精确行波解.
当Δ >0时有


注对于本节情况,若辅助方程(15)的λ1=0,变换可以得到

实际上,(20)是双曲正切函数展开法的辅助方程,只需要令即可.也就说,双曲正切函数展开法可以由本文所给方法进行改进,并且辅助方程(20)同样适用于本方法.
§4 改进辅助方程法―展开法在变系数mKdV 方程中的应用
变系数mKdV方程

可用于非调和晶格中描述等离子和声子多重作用的孤立子模型.对于该方程而言,可以直接进行有理变换,则得到类似于上一节情况,故本节不再说明,而本节选取的辅助方程是展开法中的(25).
同样引入(9),代入到方程(21)后对x进行积分并且取积分常数为0,将其化成等价形式



其中b3和b4为任意非0常数.
最后将行波变换以及辅助方程(25)带入到解(24)中,再根据辅助方程的解(26)和代数方程组的解(28),可以得到如下所示的变系数mKdV方程的精确行波解.
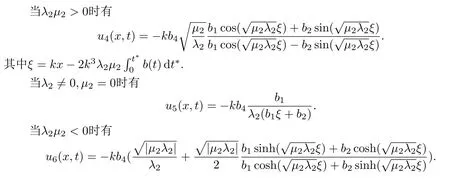
§5 改进辅助方程法―椭圆函数法在变系数fKdV方程中的应用
本节以变系数fKdV方程

为例,所引入的辅助方程为第四类椭圆方程(32).
首先引入(9)代入到式(29)后对x进行积分并且取积分常数为0,将其化成等价形式

其次取Φ和Ψ为的最高幂次项,可以得到类似于(13)的关系,再根据有理变换得到解

然后做行波变换G(x,t)=G(ξ),同样有ξ=kx+ω(t),G(ξ)为辅助方程

的解,其中c1,c2,c3为常数.文献[8]给出了方程(32)的多个精确解,并且在[13]中作者将该方程的解进行了等价性证明和分类,故方程(32)的解如下.


其中c4为任意常数.
最后由行波变换,式(31),式(34)和辅助方程(32)及其解,可以得到如下所示的非线性方程(29)的精确行波解.


§6 解及图像的简要分析
本文运用改进辅助方程法得到了有理函数,三角函数和双曲函数解.由于变系数KdV方程和mKdV方程的解较为常见,并且在文献中有所体现,故本文仅对变系数fKdV方程的部分解进行图像展示和说明.图1-图6分别是解u7-u12的图像,其左侧图为三维图像,而图1-图4的右侧图是取t=0时的二维图像,图5和图6的右侧图是取x=0时的二维图像.通过对ci(i=1,2,3,4)取值,和d(t)取不同的函数时,得到了一些孤子解.图1,图4是孤子解,图2,图3是扭曲孤子解,图5,图6是周期亮孤子解.

图1 解u7的演变: c1=1,c2=4,c3=4,c4=1,d(t)=t,k=1

图2 解u8的演变: c1=1,c2=2,c3=1,c4=1,d(t)=t,k=1

图3 解u9的演变: c1=1,c2=4,c3=4,c4=1,d(t)=t,k=1

图4 解u10的演变: c1=1,c2=4,c3=4,c4=1,d(t)=sin(t),k=1

图5 解u11的演变: c1=1,c2=2,c3=1,c4=1,d(t)=+sin(t),k=1

图6 解u12的演变: c1=1,c2=2,c3=1,c4=1,d(t)=sin(t),k=1
§7 总结
本文成功地将有理变换融入到辅助方程法中,使几类辅助方程法拥有统一的求解过程.与其他的方法相比较,本文所给出的方法将多个待定未知量省去,极大的简化了计算量,并且使用符号计算机系统Mathematica,成功地使计算过程变得清晰简洁,具有简单易懂,计算量较少,易于求解的特点,并且在求解变系数发展方程时更具有优势.故本文为变系数非线性发展方程的研究提供了一个新的思想,并且为更高阶更高维的变系数方程进一步开拓了研究与探索的新思路.
