考虑治疗和复发的类年龄结构结核病的最优控制模型

刘利利 ,张 剑 ,李雅芝 ,杨俊元

(1.山西大学 复杂系统研究所,山西太原 030006;2.黔南民族师范学院 数学与统计学院,贵州都匀 558000)

§1 引言

传染病长期以来威胁着人类健康,给社会造成沉重的经济负担.结核病是由结核分枝杆菌感染引起的一种呼吸道传染病,是全球十大死因之一,也是单一感染源的主要死因.世界卫生组织发布的2020 年度《全球结核病报告》显示,2019年我国约有83.3万人新发现结核病,其中3.3万人死亡[1].我国结核病防控形势依旧严峻.

借助传染病动力学的理论和方法对结核病进行定性和定量研究,揭示其发展和传播机制,从而为人们制定防控策略提供理论依据[2-4],这是传染病理论研究的一个重要内容.近年来,已有学者将最优控制理论用于分析结核病的传播问题.最优控制理论是数学的成熟分支之一,广泛应用于工程和其他科学分支.该理论研究结核病传播问题的工作比较少,文献[5]首次利用优化控制分析结核病的传播,建立了一类具有两菌株的结核病模型,以潜伏和感染者的人数最少和治疗成本最低作为目标,设计最优治疗的控制策略.自此以后,有学者开始关注结核病优化控制模型的研究,如: 文献[6]考虑了具有外源感染和快慢进程的结核病模型,以对潜伏感染者进行治疗为优化策略,从而降低基本再生数.文献[7]考虑了具有重复感染和外源感染的结核病控制模型,设计了两种优化控制策略.上述工作均是基于庞特里亚金极大值原理分析最优控制存在的必要条件,所研究的模型是均匀混合的常微分结核病模型.

年龄是传染病传播过程中不可忽视的因素,很多学者已经研究了年龄结构的传染病模型的阈值动力学行为[8-11].由于年龄结构的传染病模型是偏微分方程和常微分方程的耦合系统,状态空间是 无穷维空间,不具有紧性,传统的庞特里亚金极大值原理不再适用于该问题,因此研究其最优控制问题的难度较大,很难找到收敛到优化集和优化状态的序列.近年来,已有学者对年龄结构传染病模型进行优化控制研究.郭中凯等在文献[12]中研究了年龄结构SIR传染病模型的最优接种和治疗问题,Yang等在文献[13]中研究了具有多传播途径的年龄结构霍乱模型的稳定性和最优控制问题.Cao等在文献[9]中研究了潜伏者具有年龄结构和康复者具有复发的结核病模型,建立模型

其中S(t),E(t,a),I(t),R(t)分别表示易感者,潜伏者,感染者和康复者在时刻t的数量,初始条件S0,I0,R0∈R+,且E0(a)∈L1((0,∞),R+).易感者的输入率为Λ,传染率为β,自然死亡率为μ,感染者因病死亡率为δ,α(a) 表示依赖年龄的潜伏者到感染者的转化率,γ表示潜伏者到康复者的转化率,感染者的治愈率为θ,康复者的复发率为k.文献[9]主要研究了模型解的适定性,无病平衡态和正平衡态的局部稳定性和无病平衡态的全局稳定性.

本文将进一步考虑模型(1)的最优控制问题,从感染者和康复者出发,研究结核病的药物治疗和康复者复发的最优控制策略.

§2 结核病优化控制模型

基于上面的分析,考虑感染者的药物治疗和康复者复发,本文建立如下潜伏者具有年龄结构的结核病优化控制模型

其中γ(a)表示依赖年龄的潜伏者到康复者的转化率,A表示潜伏者控制的终止年龄,u1(t),u2(t)是Lebesgue可积函数,代表优化控制变量.其他参数的生物意义与模型(1)相同.应用文献[9]中模型适定性分析过程,可以得到模型(2)的适定性.即

引理2.1当t ＞0时,系统(2)的所有解都是非负且有界的.

§3 控制策略

本节将利用Gateaux导数和Ekeland变分原理分析结核病模型的最优控制问题.

控制变量记为U(t)=(u1(t),u2(t)),定义控制集为

其中T代表控制的终止时刻.定义目标函数

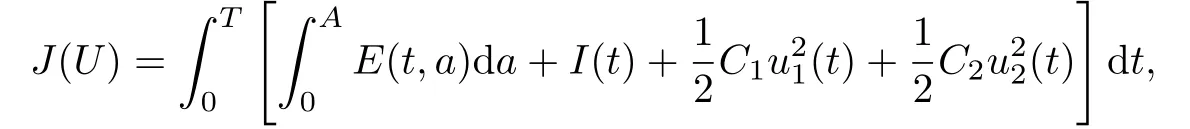
其中C1与C2是权重系数,表示控制所投入的成本,这里假设采取措施消耗的费用为非线性二次函数.控制目标是找到最优控制U*使得J(U*)最小,即潜伏者和染病者数目最少且控制投入成本最低.

3.1 最优控制的存在性

通过如下定理证明最优控制的存在性.

定理3.1存在最优控制使得J(U*)=minU∈U J(U).

证显然控制集U非空且是闭凸的.令X=(S(t),E(t,a),I(t),R(t))T.假设

则优化控制模型(2)的右端可以写成ρ1(X)+ρ2(X)U的形式.进一步,目标函数的被积函数记为. 显然,L(X,U)在控制集U上关于U(t)是凸的.根据文献[14]中定理4.1可以得到最优控制U*的存在性.

3.2 伴随系统

Gateaux导数是求解系统(2)伴随系统的一个重要方法.令l(t)=(l1(t),l2(t))是控制集U在U处的切锥,l1(t),l2(t)∈(0,1).对于充分小的常数ξ ＞0,定义辅助控制变量Uξ=由于状态变量关于控制变量是连续依赖的,则有(S,E,I,R)=(S,E,I,R)(u1,u2)和.因此,系统(2)可以改写成如下形式

当ξ →0+时,可以得到状态变量的弱导数是

为求系统(2)的伴随系统,引入与系统(2)相对应的伴随变量λS(t),λE(t,a),λI(t) 和λR(t).利用条件,λS(T)=0和分部积分法,对系统(4)的第一个方程进行运算得到

目标函数J(U)关于控制变量U的Gateaux导数为

结合等式(5)-(9),可以得到系统(2)的伴随系统

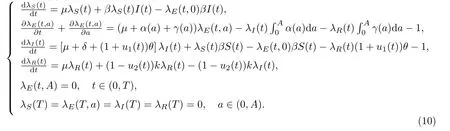
进一步,系统(10)存在一个弱解,记为

且此弱解Lipschitz连续.

3.3 最优控制的形式

现在给出最优控制的具体形式.

定理3.2若存在U* ∈(L∞(0,T))2使得J(U) 取得最小值,那么

证将系统(10)代入方程(9)中,可以得到

将方程(5)-(8)带入方程(11),则对于所有U ∈U,有

进一步考虑控制变量的上下界,得到J(A)取得最小值的最优控制是

3.4 最优控制的存在唯一性

年龄结构的传染病模型是一阶偏微分方程,由于其状态空间不具有紧性,故很难找到收敛到优化集和优化状态的序列.为了克服该困难,本文采用Ekeland变分原理[15]寻找近似函数的最小值.定义下面的辅助目标函数

采用[16]的理论方法和文献[13]的思路,得到使Jε(u)取最小值时最优控制的存在唯一性,即有下面的定理

定理3.3若Jε(u) 存在最优控制使其取得最小值,那么

由Ekeland变分原理及L∞空间上的Lipschitz估计,得到最优控制的存在唯一性.

定理3.4若T/C1和T/C2足够小,那么存在唯一的最优控制使J(U) 取到最小值.

其中B是常数,取决于状态方程与伴随方程的解以及Lispschitz常数.类似可得

如果T/C1足够小,那么

从而当ε →0+时,.由Ekeland变分原理,则有当ε →0+时,J(U*)≤infU∈U J(U).

§4 数值实验

在本节中,主要对最优控制进行数值模拟以论证优化控制策略的合理性.为此使用差分法结合伴随系统和状态系统进行数值模拟.为了进行最佳状态下的数值模拟,采取较小的时间和年龄步长,即Δt=Δa=0.05,并假设最大年龄为60,对患者进行365天的优化控制.模型的初始值为S(0)=9800,I(0)=10,T(0)=100,E(0,a)=320 cos2(0.46a),权重系数C1=C2=10.最后,根据文献[9],定义了部分参数,如表1所示

表1 数值模拟中的参数

图1表示最优控制率(u1与u2)随时间变化的曲线图.由图1可以观察到在结核病的优化控制中,复发率的优化控制在短时间(实施控制的第100天左右)由控制的下界达到控制的上界,而治愈率的优化控制以较慢的速度(实施控制的第135 天左右)才达到控制的上界.

图1 最优控制率随时间的变化

图2表示最优控制策略对结核病感染人数的影响.为此,设计了四种不同的最优控制情形.在情形1(没有任何控制措施,即u1=u2=0),第60天左右结核病感染人数达到最大值,感染人数持续在高感染水平并且是缓慢下降;在情形2(只有最优治愈控制措施,即u10,u2=0),第50天左右结核病感染人数达到最大值,染病人数开始持续下降到第100天,染病人数下降的趋势则变得很慢;在情形3(只有最优复发控制措施,即u1=0,u20),第45天左右结核病感染人数达到最大值,染病人数开始迅速下降到第200天左右染病人数开始在低感染状态缓慢下降;在情形4(最优综合控制措施,即u10,u20),第40天左右结核病感染人数达到最大值,染病人数迅速下降,并且很快(第190天左右)达到无感染的稳定状态.类似分析可以得到不同最优控制策略对结核病复发人数的影响.对比情形2和情形3,可以知道只有最优复发控制(u2)比只有最优治疗控制(u1)的控制效果好,这说明了在实际防控结核病传播的时候,控制复发率更为重要.对比情形3和情形4,可以知道最优综合控制策略的效果最好.

图2 不同最优控制策略对感染人数和康复人数的影响

为了研究控制成本对结核病感染人数的影响.分析了3种不同控制成本的情形,如图3所示.情形1表示低成本(C1=C2=1)时,感染者与康复者的变化.在10天左右,结核病感染人数达到最大值并迅速下降,并在120天左右处于低感染状态并缓慢下降.情况2表示成本适中(C1=C2=10)的情况下,染病人数在50天左右达到峰值,并迅速下降至200天左右趋于稳定状态.在情况3中,可以看出,在高成本(C1=C2=100)的情况下,感染者迅速上升,在80天左右达到最大人数,在300天左右才达到相对稳定的低感染状态.对比三种情况可以看出,不同的成本对最优控制存在影响,由于经济状况的限制,在投入相同的情况下,成本越低,控制所达到的效果越好.

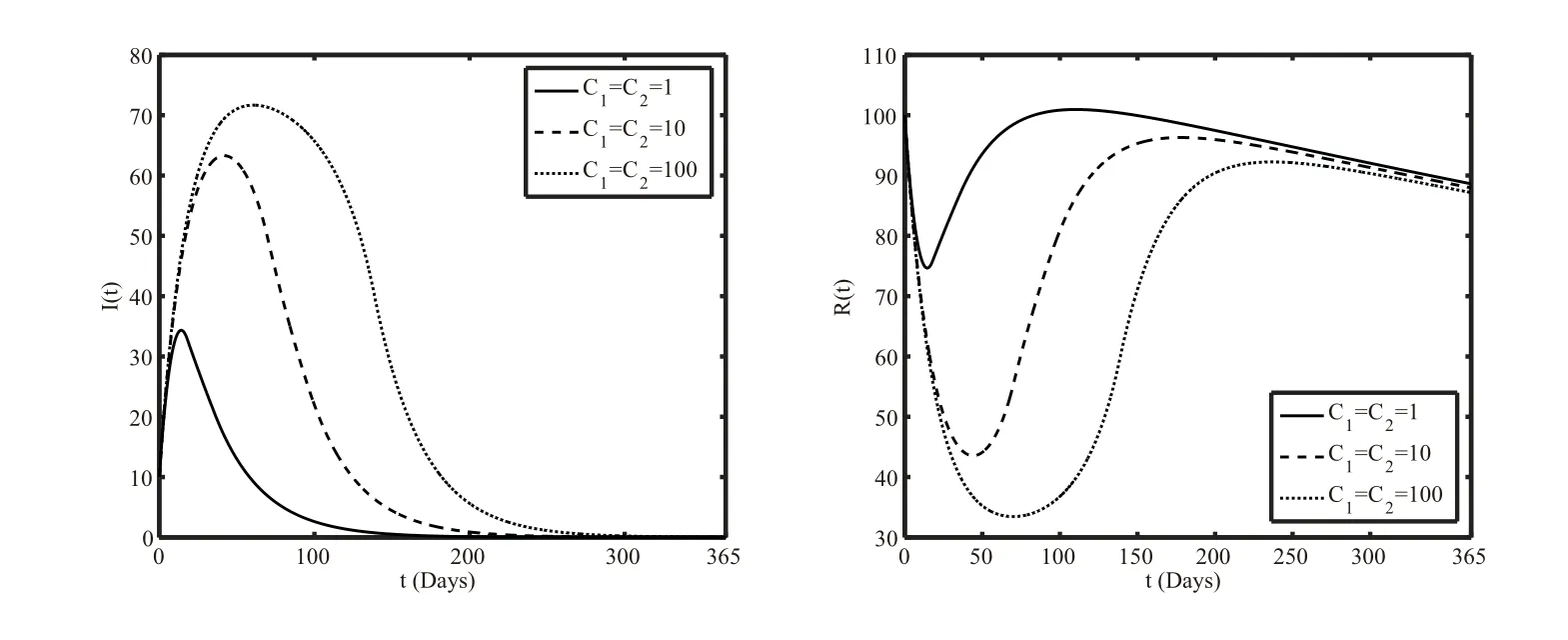
图3 不同成本下I(t)(左)与R(t)(右)的变化.(1) 低成本: C1=C2=1;(2) 中成本: C1=C2=10;(3)高成本: C1=C2=100

§5 结论

本文研究了潜伏者具有年龄结构的结核病模型考虑治疗和复发的最优控制模型.通过建立目标泛函,利用Gateaux导数及Ekeland变分原理分别确定了最优控制的具体表达式和存在唯一性;最后结合数值模拟对比分析不同优化控制和控制成本对结核病感染人数和康复人数的影响;结果发现: 几种最优控制的效果,最优综合控制最好,最优复发控制次之,并且控制成本越低,效果越好.