异步切换下切换时变时滞系统的保成本控制

李同彬, 高 娟

(1. 哈尔滨师范大学经济学院，哈尔滨 150001; 2. 哈尔滨师范大学数学科学学院，哈尔滨 150001)

0 引言

切换系统由一系列连续时间或离散时间子系统和一个控制它们之间切换的切换信号组成。不仅在传统的应用领域，如航天和汽车工程等领域广泛应用，也频繁地应用于新兴的领域，如计算机科学和计算机网络、电源转换器、活性污泥废水处理系统、开关连续搅拌釜反应器等。因此，切换系统的研究具有重要的理论及实践意义。近年来，切换系统越来越受到重视，研究结果可参阅文献[1–6]。由于时滞现象广泛存在工程系统中，具有时滞的切换系统一直是控制界研究的热点[7–8]。学者们提出了很多有效的研究切换系统的方法，如二次Lyapunov 函数法、多Lyapunov 函数方法[9–10]、平均驻留时间技术[11–13]、线性矩阵不等式方法等[7,14]。

上述所有研究工作都假设控制器与子系统同步切换。然而，在实际操作中，系统在识别子系统并请求控制器切换到该子系统相应的控制器的过程需要花费一段时间，这种子系统和控制器“异步切换”的现象是不可避免的[15]。关于异步切换下的切换系统研究有很多，如稳定性分析[16–19]、故障检测[20]、滑模控制[21]、输出跟踪控制[22]、输出反馈控制[23–24]、H∞滤波[25]。然而，据我们所知，异步切换下具有时变时滞的切换系统的保成本控制问题尚未得到研究，这启发了本研究。保成本控制是设计控制系统以实现系统稳定性和足够水平的鲁棒性能的一种实用方法[26]，学者们对不同系统的保成本控制问题进行了研究，如非线性系统[26]、网络控制系统[27]、不确定切换时滞系统[28]、切换非线性系统[29]、切换奇异系统等[14]。

基于上述工作，本文研究了异步切换下切换时变时滞系统的保成本控制问题。与以往大多数使用普通二次Lyapunov 函数实现保成本控制的工作不同，本文采用了分段Lyapunov 函数方法，与普通二次Lyapunov 函数方法相比，具有更小的保守性。因为分段Lyapunov 函数方法的复杂性，关于保成本控制的研究很少。本文使用分段Lyapunov 函数(已被证明是处理异步切换下切换系统的有效工具[22–23])，以及平均驻留时间技术，实现了异步切换下切换时变时滞系统的保成本控制。

本文的主要工作如下：

1) 研究了切换时变时滞系统在异步切换下的保成本控制问题；

2) 采用分段Lyapunov 函数方法实现了保成本控制。

1 问题描述及引理

考虑如下时变时滞切换系统

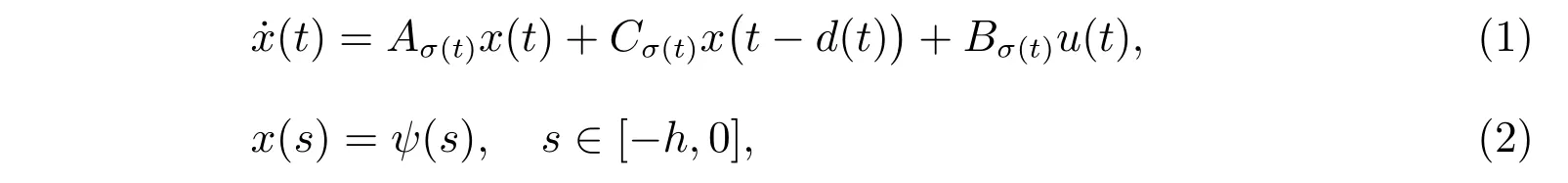
其中t ≥0,x(t)∈Rn为系统状态向量，u(t)∈Rm为系统输入向量，σ(t) : [0,+∞]→={1,2,···,N}，一个关于时间的分段常值函数，由它决定的子系统的切换序列可描述为

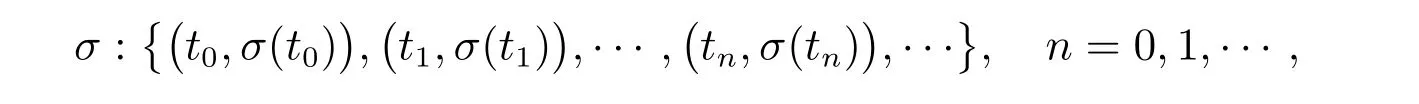
其中t0= 0 表示初始时刻，tn为第n个切换时刻。σ(t) =i表示第i个子系统运行。N表示子系统个数。Ai、Bi、Ci(i ∈)为已知的适维实值常数矩阵。ψ(s)为给定的向量值初始函数，d(t)为时变时滞且满足

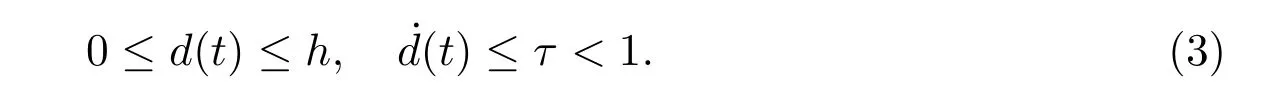
σ′(t)表示控制器的实际切换信号，控制输入为

控制器的切换瞬间滞后于子系统的切换瞬间，控制器的实际的切换序列可描述为

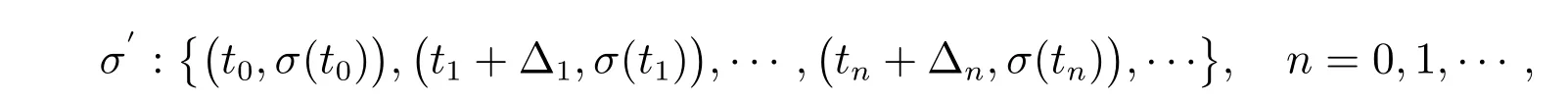
控制器相对于相应子系统的切换时滞满足

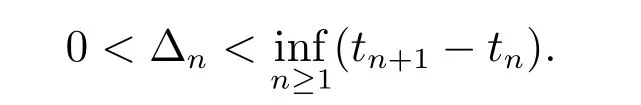
注1条件∆n＜ infn≥1(tn+1−tn)意味着异步切换系统的整个运行时间，可划分为子系统和控制器“匹配时间段”和“不匹配时间段”。在匹配时间段内，子系统和控制器同步运行，在不匹配时间段内，子系统和控制器异步运行。

在控制器(4)下，得到下面的闭环切换系统

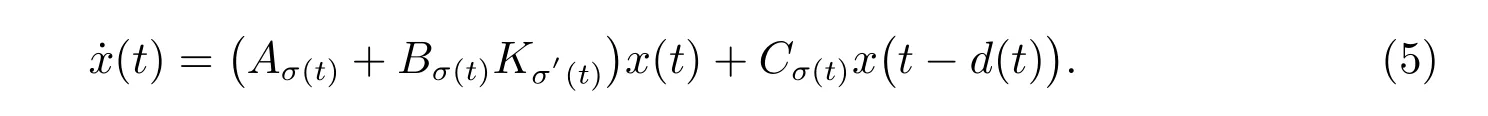
对系统(1)定义成本函数

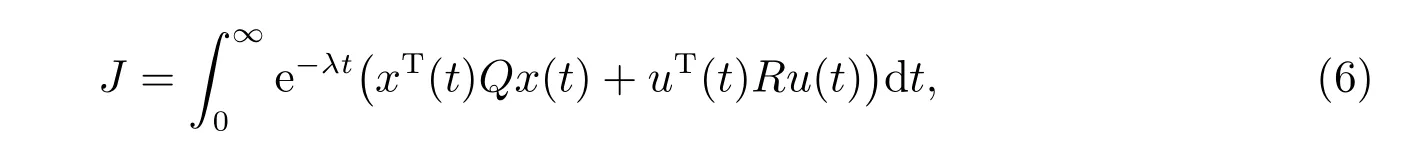
其中λ>0 为常数，Q和R为给定的正定加权矩阵。

定义1对于异步切换下的时变时滞系统(1)，如果存在控制律u(t)和一个正数J∗，使得闭环系统(5)是稳定的，并且成本函数(6)满足J ≤J∗，则J∗称为切换系统(1)的一个成本上界，u(t)称为切换系统(1)的一个保成本控制律。

定义2[30]如果存在常数δ ≥1 和λ>0，使得系统(1)的解满足

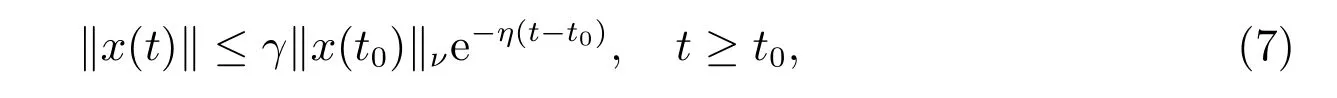
则称切换系统(1)的平衡点x∗=0 是指数稳定的，其中

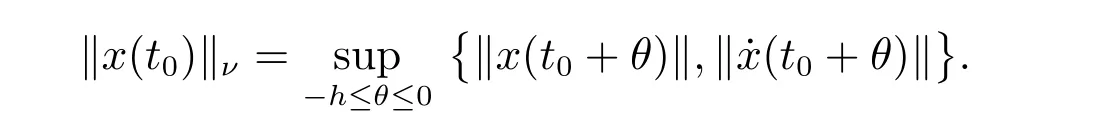
定义3[31]给定常数τa>0,N0≥0 和任意的T2>T1≥0，若不等式

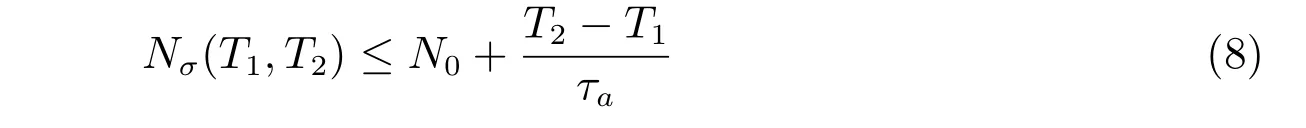
成立，则称τa为切换信号σ(t)的平均驻留时间，其中Nσ(T1,T2)为切换信号σ(t)在时间区间(T1,T2)上的切换次数，N0为颤抖界。

在实际使用时，一般取N0=0。

引理1[32]对于任意对称正定常数矩阵L ∈Rn×n和常数ω> 0，如果存在向量值函数ξ:[0,ω]→Rn，使得积分

正确定义，那么下面的不等式

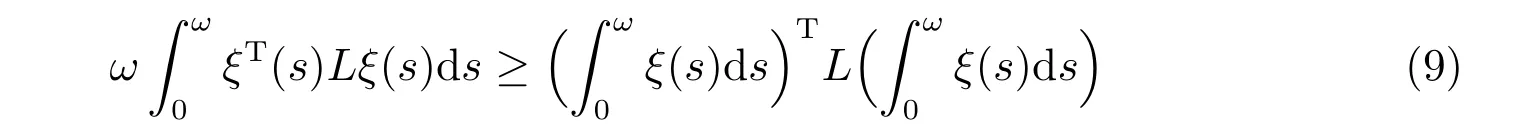
成立。

引理2(Schur 补引理) 给定一个适当维数的对称矩阵

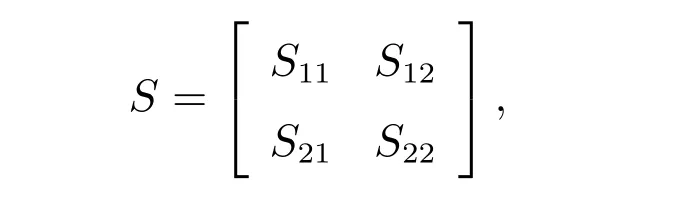
其中S11和S22均为对称矩阵，且=S21，则下列三式等价：

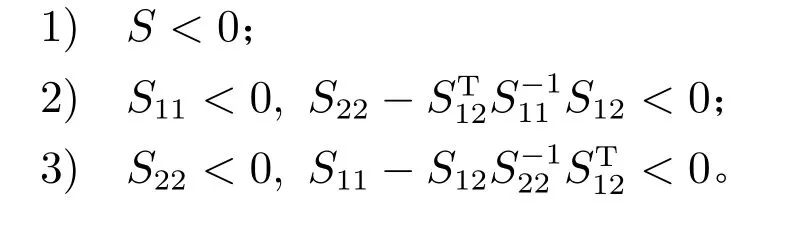
2 主要结果

假设当t=tn−1时，第i个子系统被激活，即σ(tn−1) =i，当t=tn时，第j个子系统被激活，即σ(tn) =j。由于控制器切换滞后于子系统切换，当第i个子系统切换到第j个子系统时，控制器Ki还在运行直到∆n这么长时间后，才切换到Kj。因此，闭环切换系统(5)可描述为

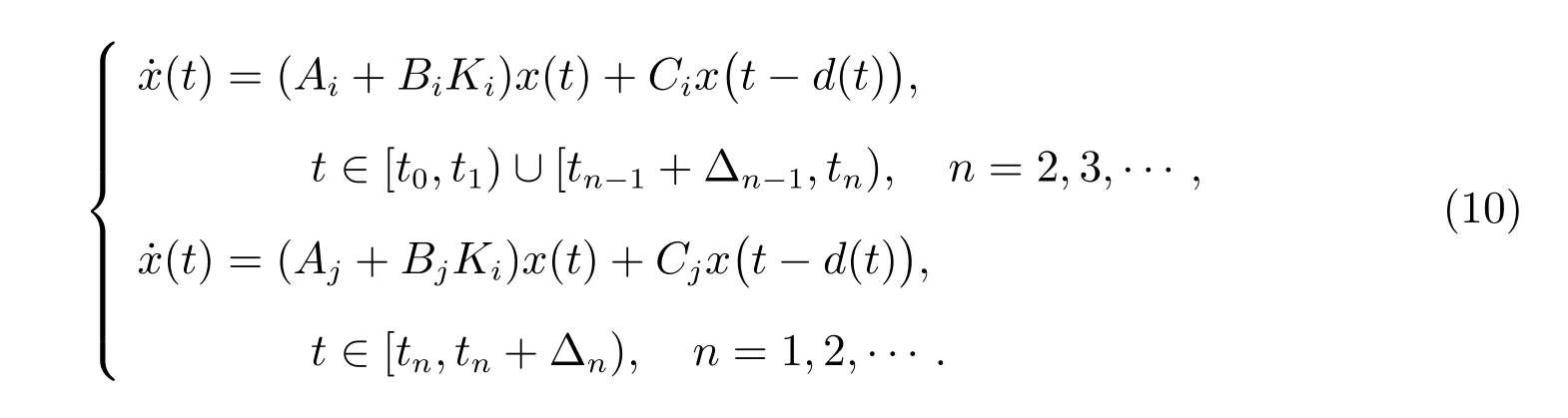
首先，利用分段Lyapunov 函数方法，给出了保证成本控制器(4)存在的一个充分条件，解决了切换时变时滞系统(1)在异步切换下的保成本控制问题。为了方便起见，令T−(t0,t)表示子系统在时间区间[t0,t)上受控于匹配控制器的总时间，T+(t0,t)表示子系统在时间区间[t0,t)上受控于不匹配控制器的总时间。

定理1考虑异步切换系统(1)，成本函数为(6)，给定正的常数α和β，µ≥1，对于任意的i,j ∈,i ̸=j，如果存在矩阵Pi>0,Si>0,Zi>0，使得下面矩阵不等式成立

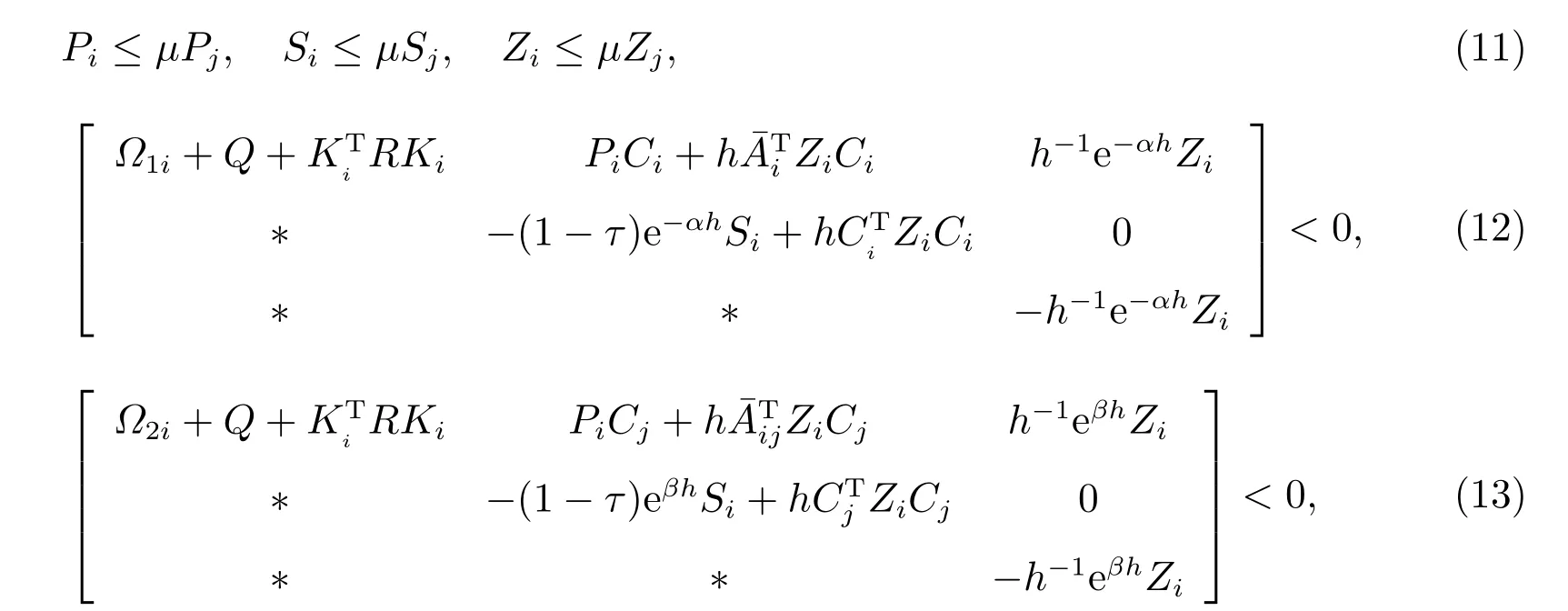
那么，对于任意平均驻留时间满足

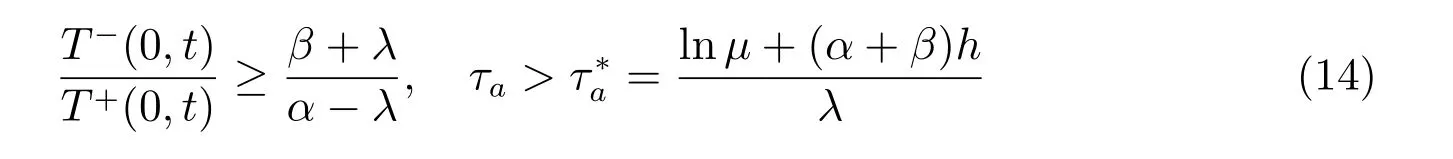
的切换信号，闭环切换系统(5)在状态反馈控制器(4)下是指数稳定的，成本函数的一个加权上界为

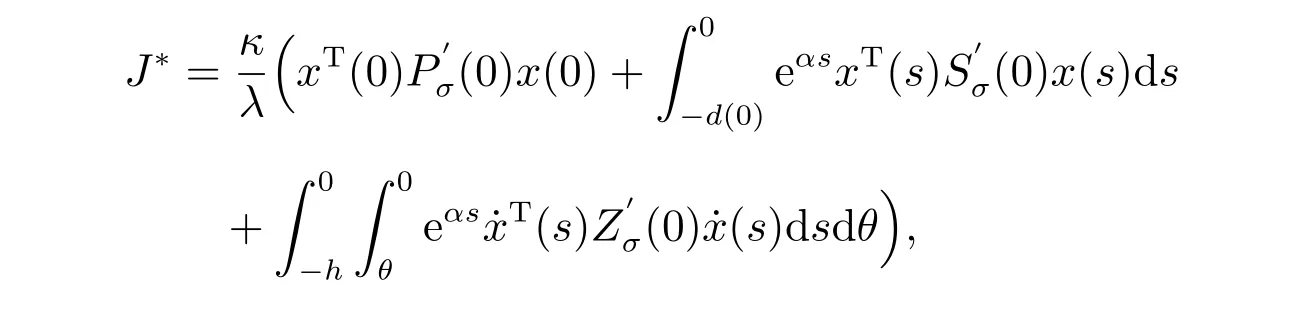
其中

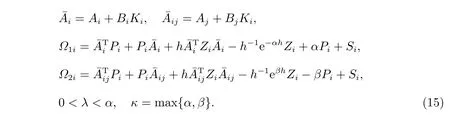
证明 稳定性分析将从控制器与子系统匹配和不匹配两方面分别进行。

当t ∈[t0,t1)∪[tn−1+∆n−1,tn),n= 2,3,···时，匹配时间段运行。选择如下Lyapunov 函数

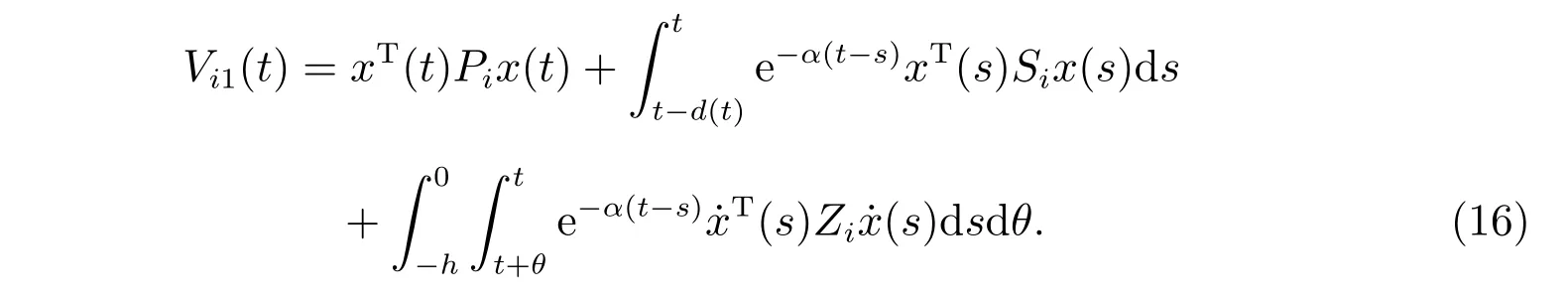
计算它的导数得

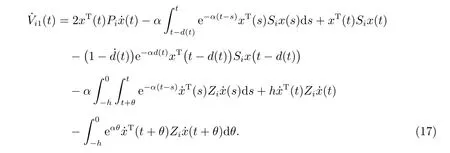
由(3)式，可得

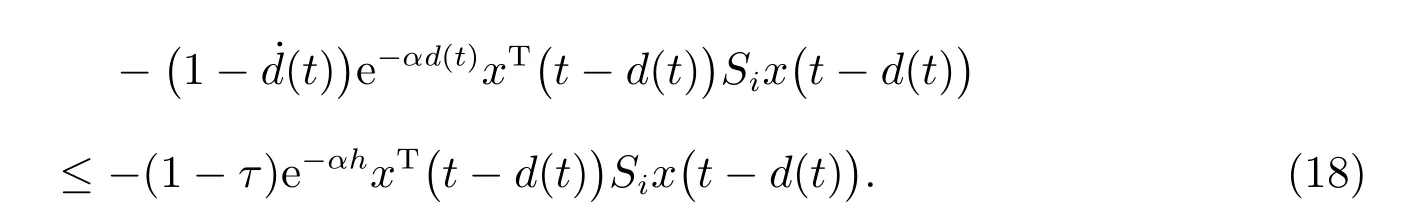
应用引理2，有

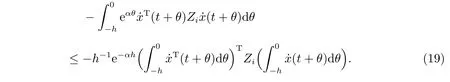
另一方面，由Leibniz 公式，可得

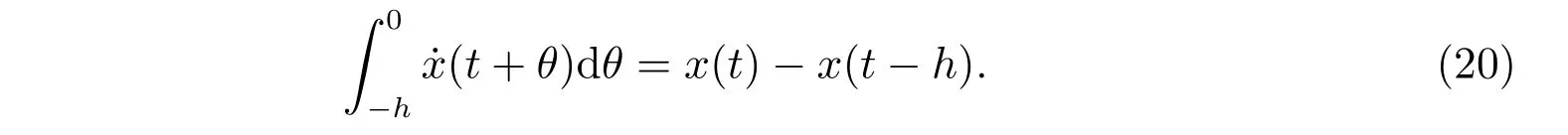
结合(17)∼(20)式，得

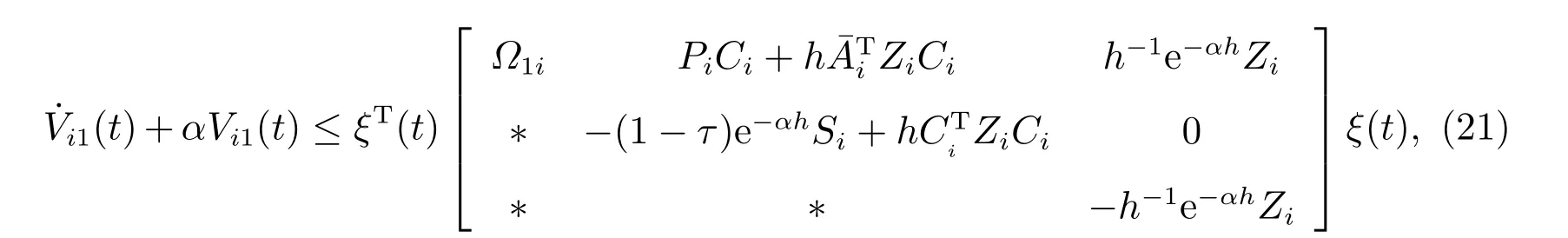
其中

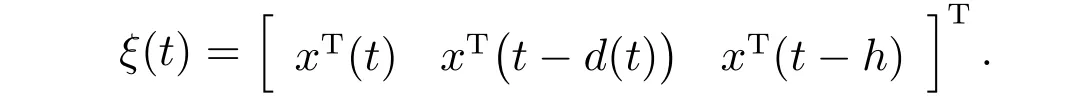
根据矩阵不等式(12)，可得

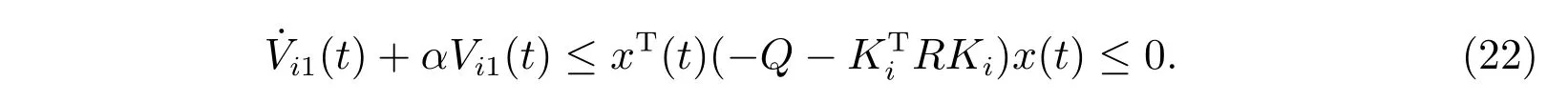
对(22)式从tn−1+∆n−1到t(当t ∈[t0,t1)时，从t0到t)进行积分，可得

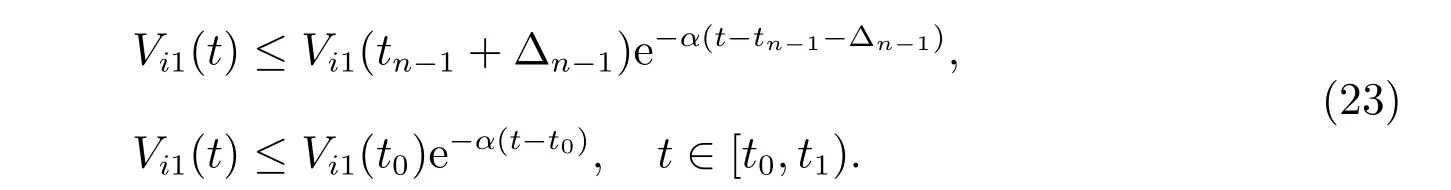
当t ∈[tn,tn+∆n),n=1,2,···，不匹配时间段运行。选择如下Lyapunov 函数

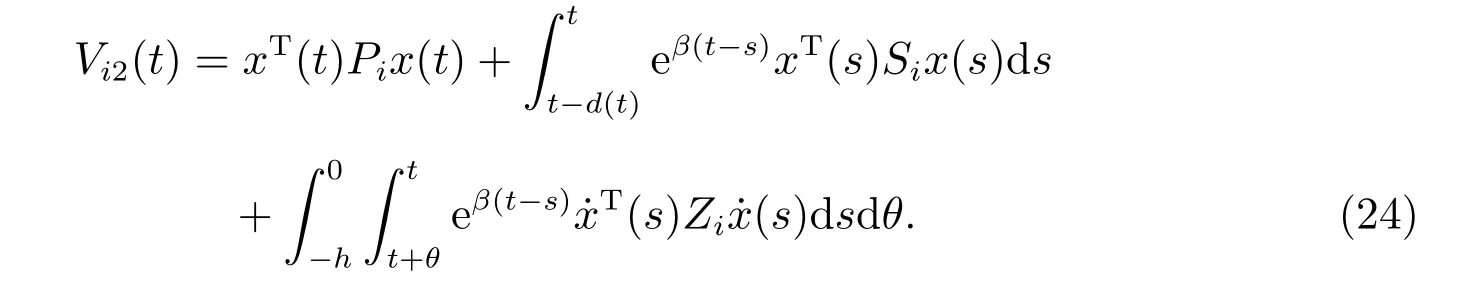
与前面类似，可得

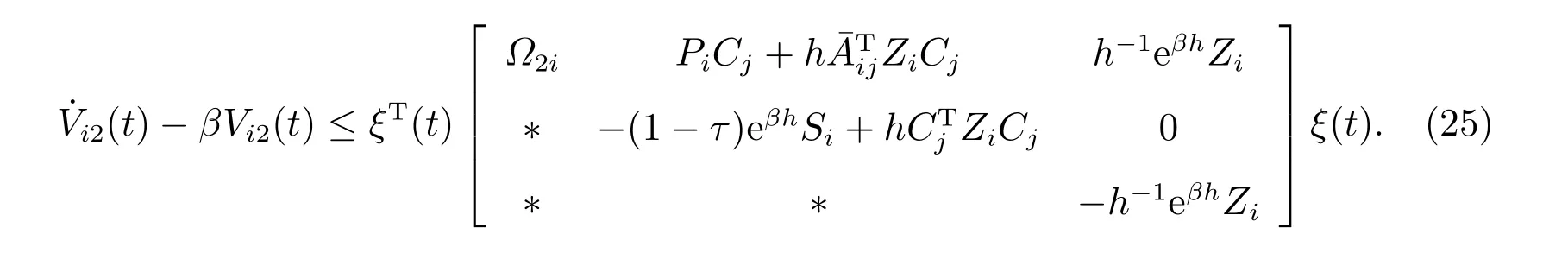
由矩阵不等式(13)，可得

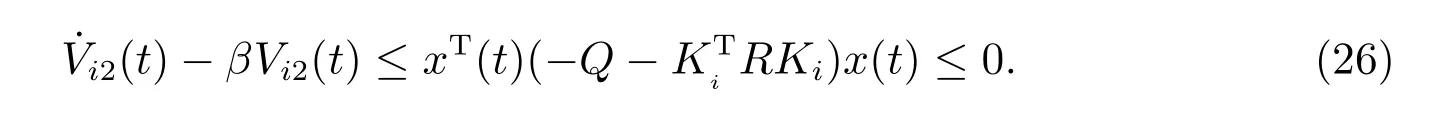
对(26)式的两边从tn到t进行积分，可得

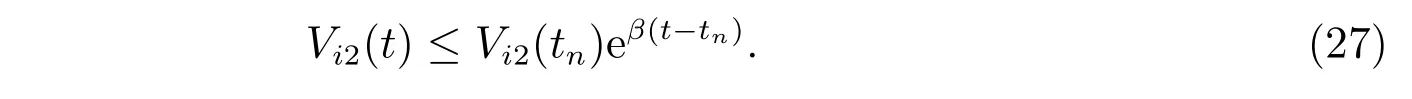
通过计算，显然有下面两个不等式

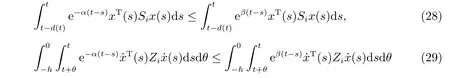
成立。由(28)式和(29)式，可得

另一方面，由(3)式，得

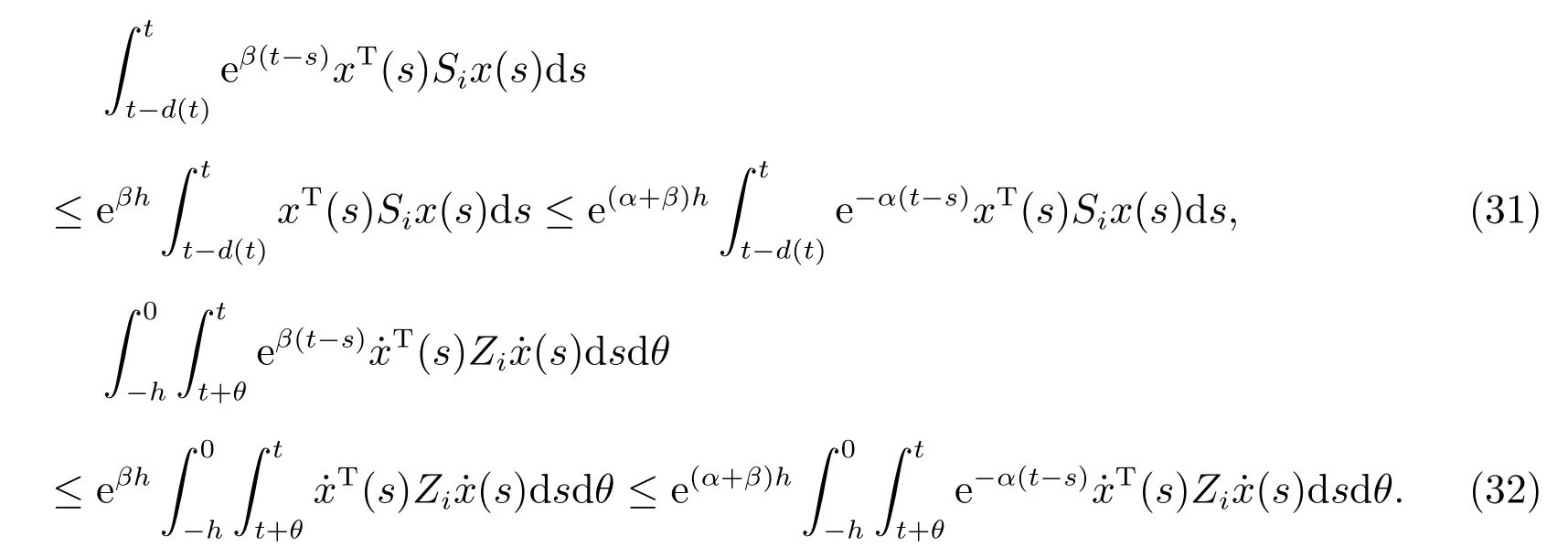
由(31)式和(32)式，可得

用(11)式计算，有

由(30)式和(34)式，有

对于整个区间[t0,t)，考虑如下分段Lyapunov 函数

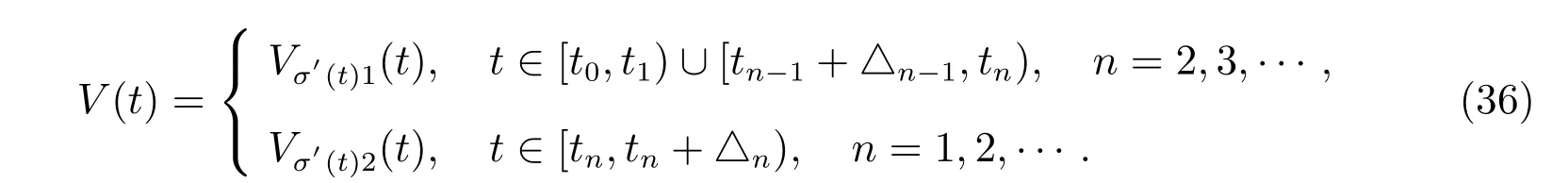
结合(23)式、(27)式、(33)式和(35)式，当t ∈[t0,t1)∪[tn−1+△n−1,tn),n=2,3,···时，我们可得

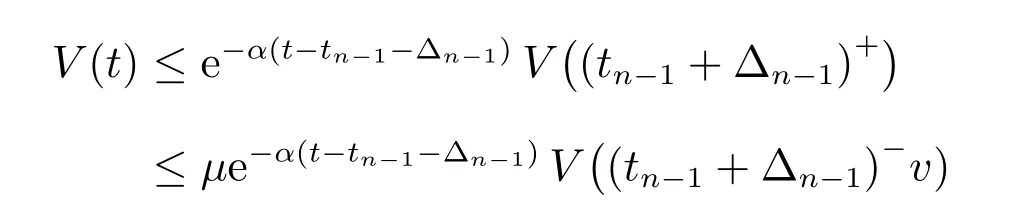
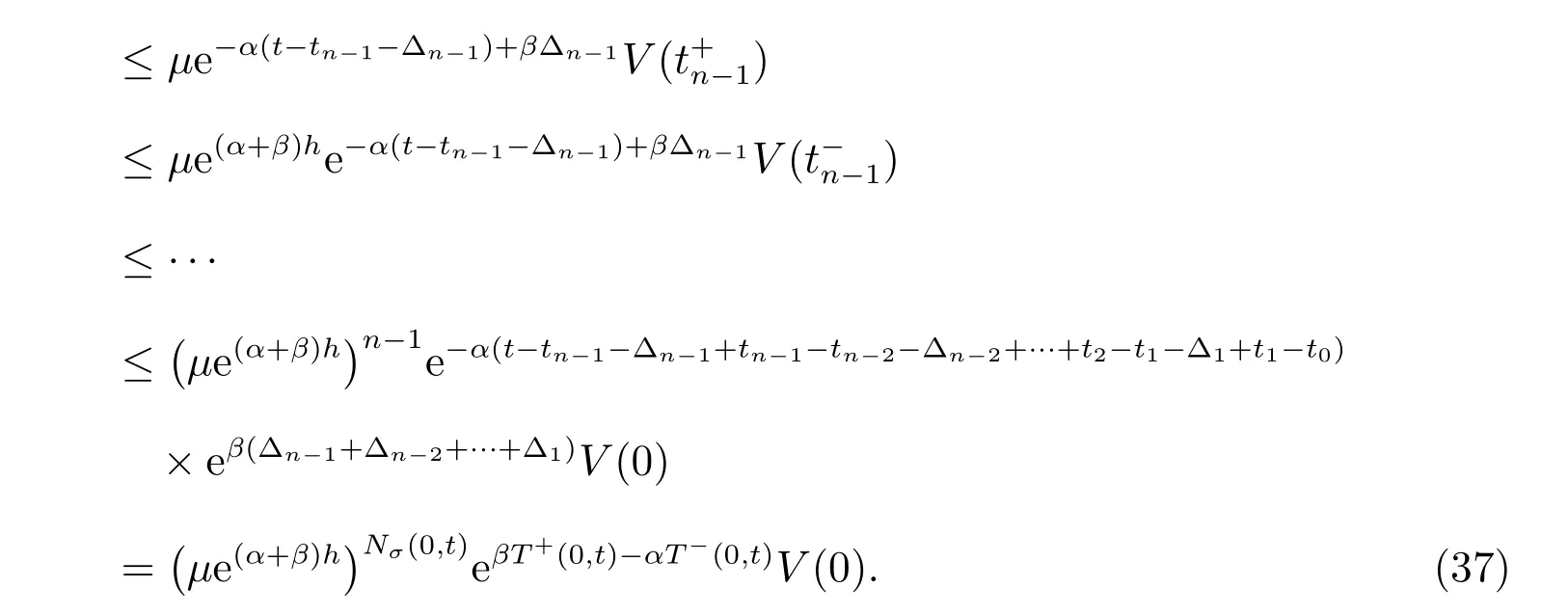
根据定义3和(14)式，有

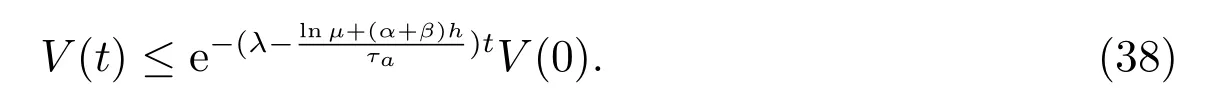
进一步，可得

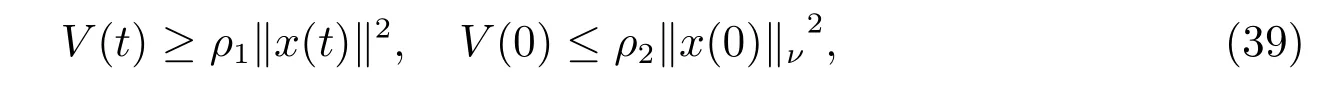
其中

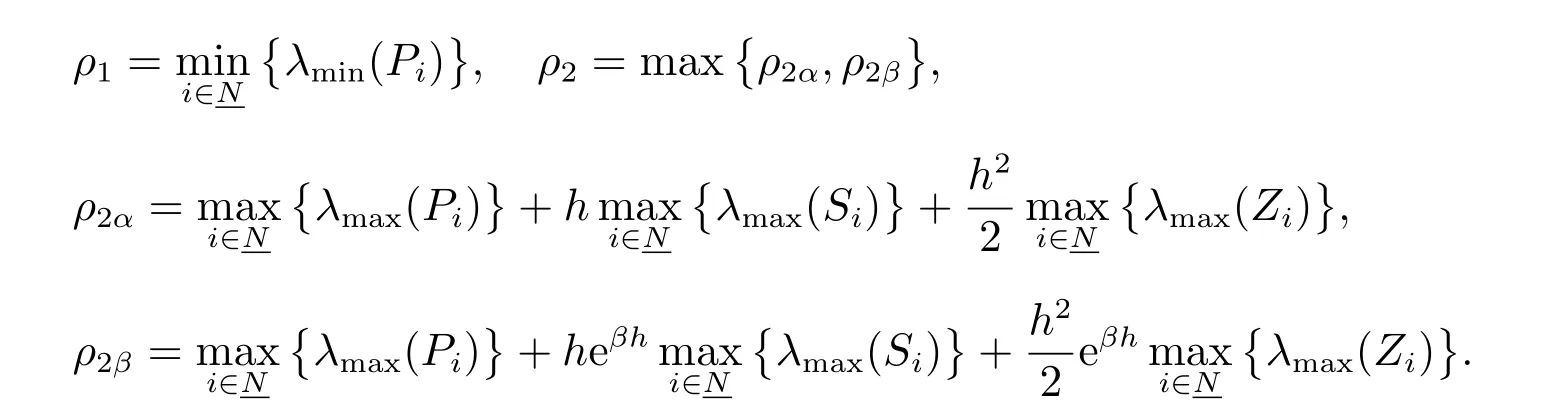
由(38)式和(39)式，得到

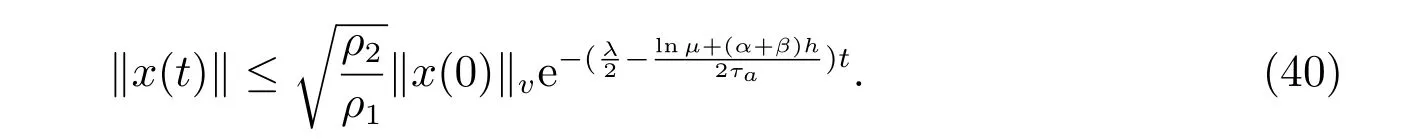
当t ∈[tn,tn+△n),n=1,2,···时，可得

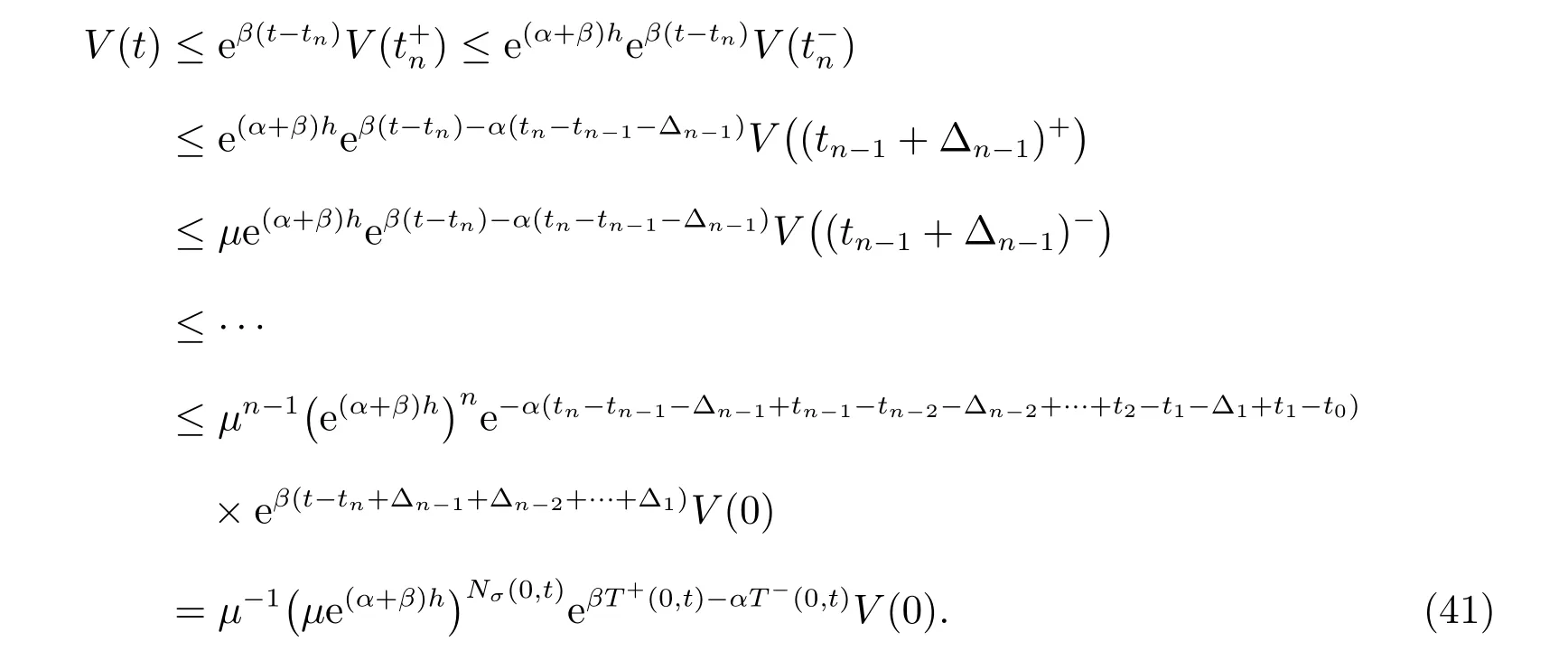
由定义3 和(14)式，我们有

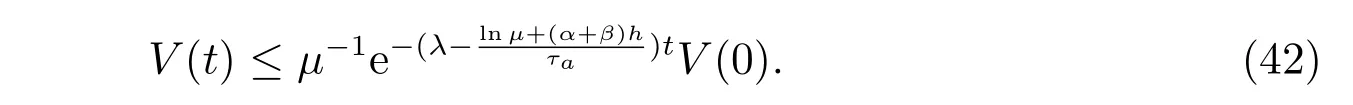
由(39)式和(40)式，可得

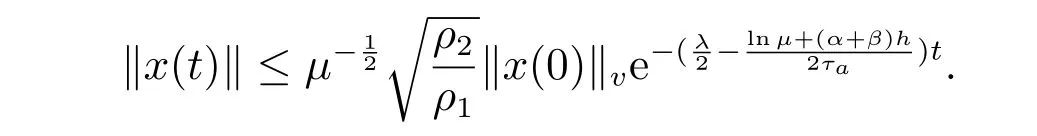
由定义2 和(14)式，闭环系统(5)是指数稳定的。

另一方面，由(22)式和(26)式，有

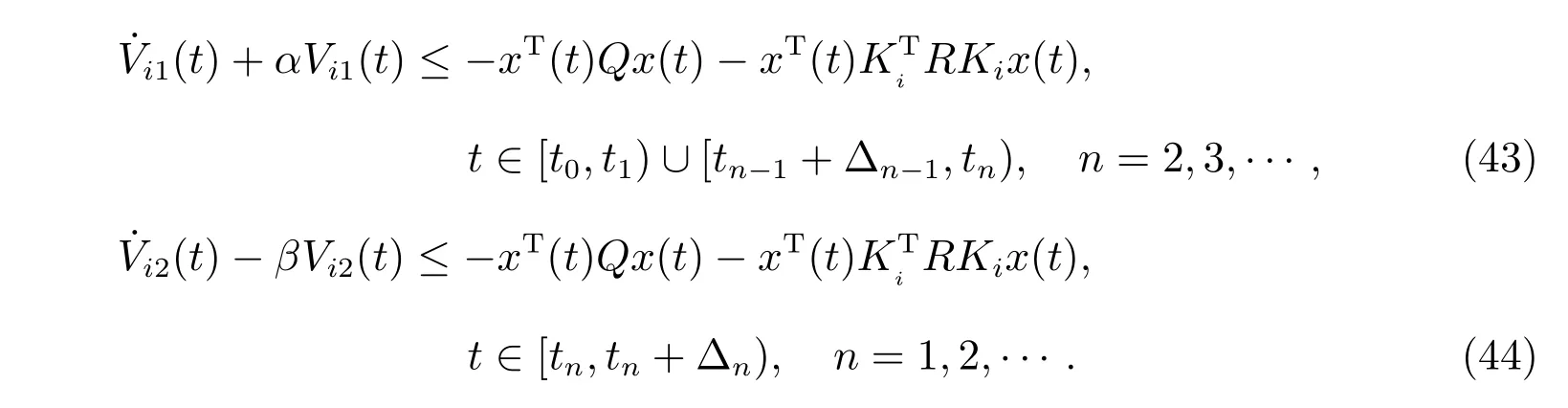
对(43)式两边从tn−1+∆n−1到t(当t ∈[t0,t1)时，从t0到t)进行积分，对(44)式从tn到t进行积分，得到

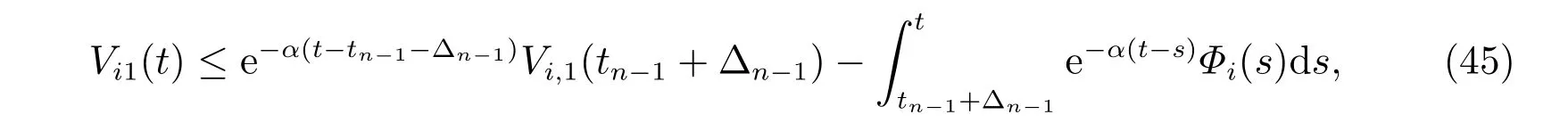
或

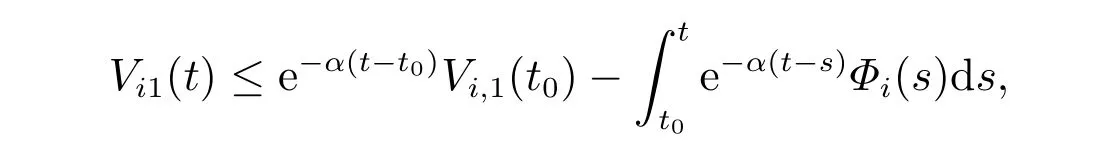
以及

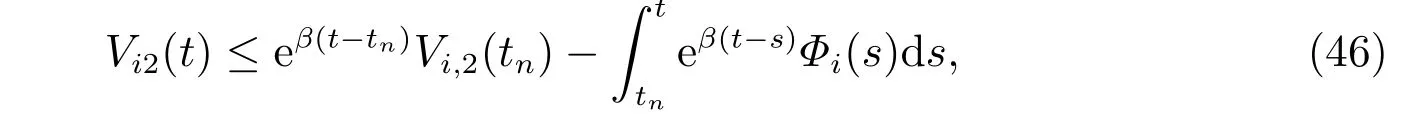
其中

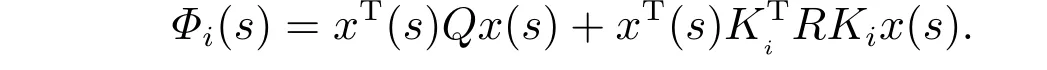
当t ∈[t0,t1)∪[tn−1+△n−1,tn),n=2,3,···时，由(33)式、(35)式、(45)式和(46)式，我们可得

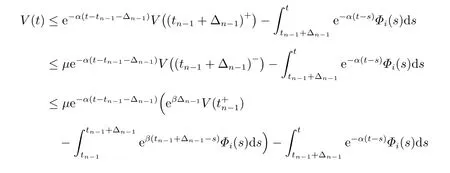
对(47)式两端乘以e−(lnµ+(α+β)h)Nσ(0,t)，可得

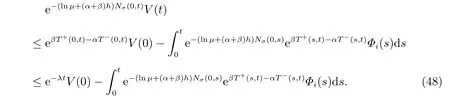
由(8)式和(14)式，有

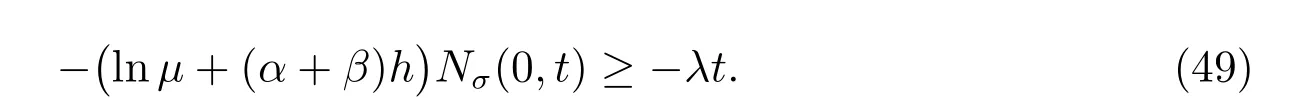
因此，(48)式可以写为

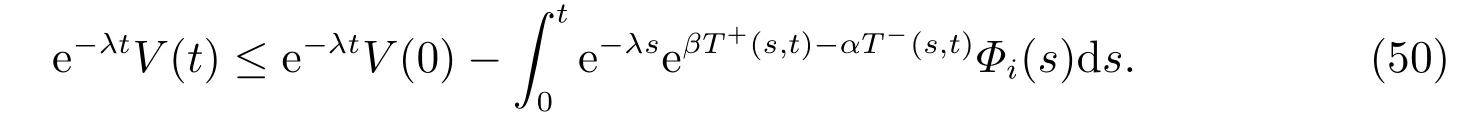
注意到

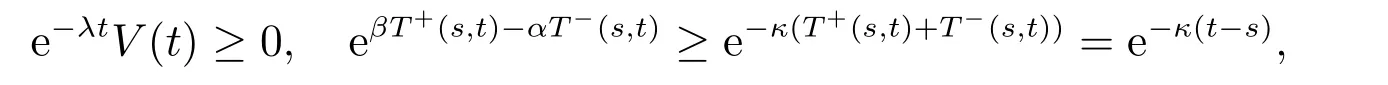
我们有

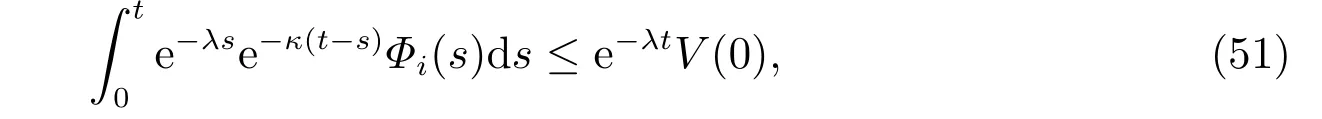
其中κ已在(15)式中定义。

分别对(51)式两端从0 到∞积分，得到

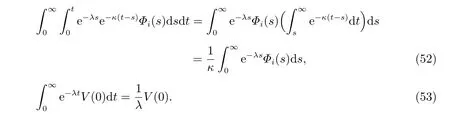
显然可得

当t ∈[tn,tn+△n),n=1,2,···时，我们有

(55)式两端乘以e−(lnµ+(α+β)h)Nσ(0,t)，可得

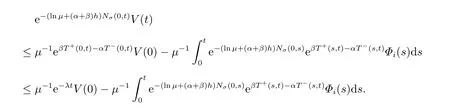
由(49)式，可得

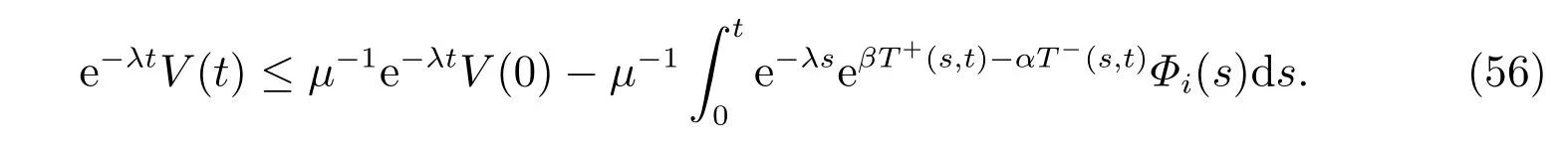
注意到

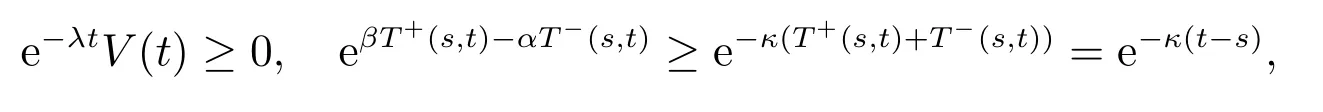
我们可得(51)式。所以，最终可得(54)式。由定义1，可知

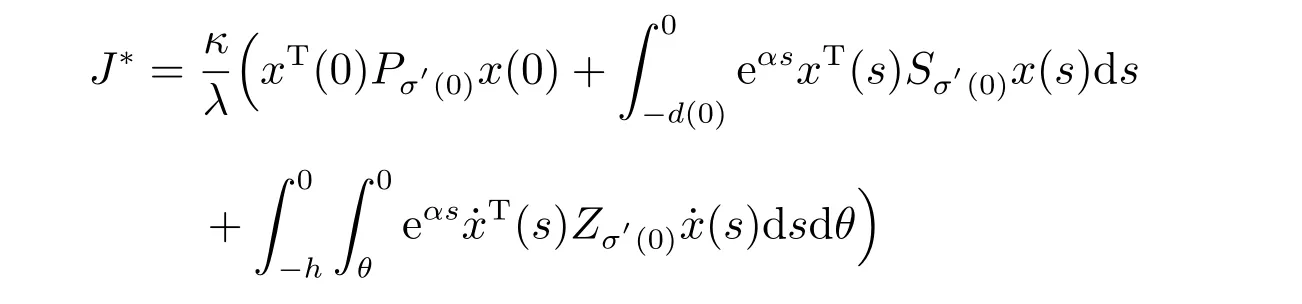
是系统(1)的一个成本上界。

注2对比文献[14,28]的结果，在文献[14,28]中，使用公共二次Lyapunov 函数来实现保成本控制。相较公共Lyapunov 函数法，本文定理1 中使用的分段Lyapunov 法不但能实现保成本控制，而且保守性更低。

下面给出保成本控制器设计的线性矩阵不等式条件。

定理2考虑异步切换系统(1)，成本函数(6)，给定正的常数α,β,µ≥1，对于任意的i,j ∈,i ̸=j，如果存在矩阵Xi>0,Ni>0,Li>0 和矩阵Mi，使得下面的线性矩阵不等式成立

那么，对于任意平均驻留时间(14)，闭环切换系统(5)在状态反馈控制器(4)下是指数稳定的，成本上界为

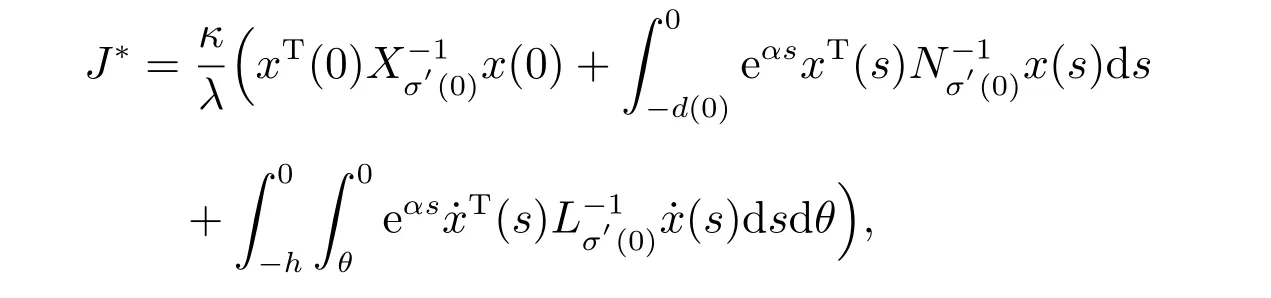
其中

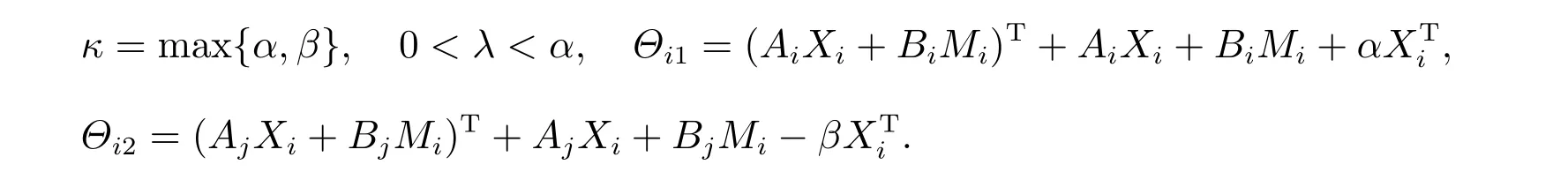
控制器增益为

证明 由Schur 补引理，矩阵不等式(12)等价于

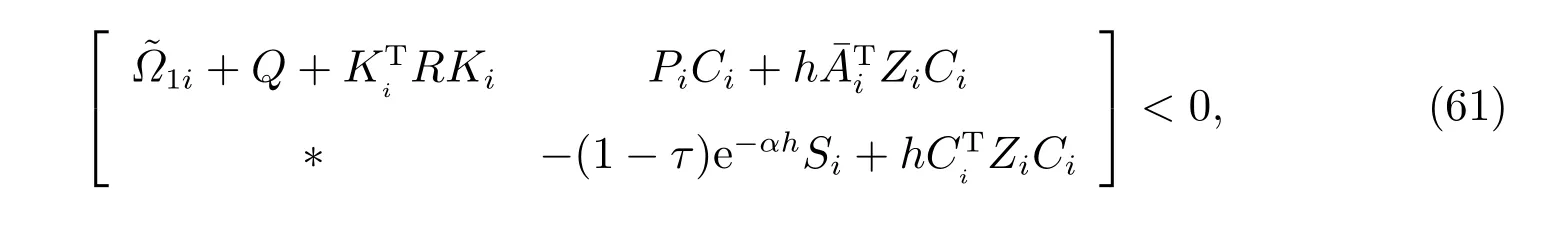
其中

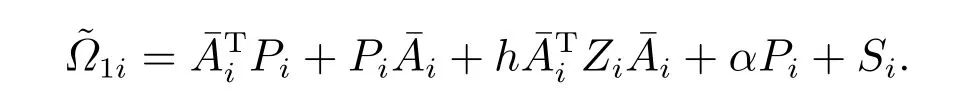
那么，(61)式等价于

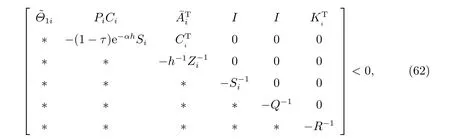
其中

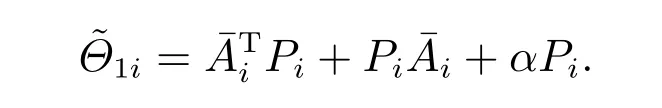
(62)式的两端分别左乘对角矩阵

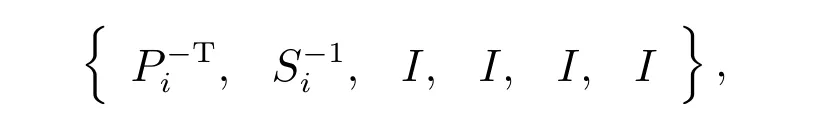
右乘对角矩阵

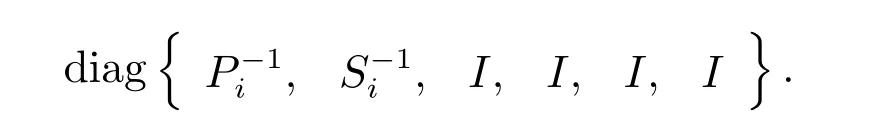
记

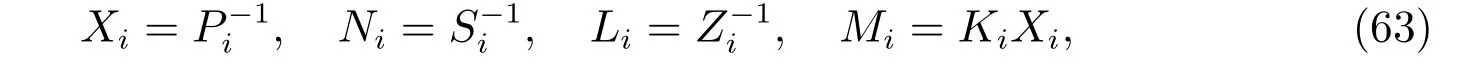
可得矩阵不等式(58)成立，这意味着(12)式等价于(58)式。以类似方式，(13)式等价于(59)式。

3 数值仿真

本节通过一个数值例子来验证本文结论的有效性。

考虑由两个子系统组成的切换系统，子系统矩阵参数为

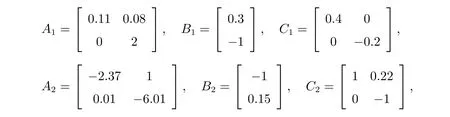
d(t) = 0.1 + 0.1 sint，易得h= 0.2,τ= 0.1。初始值ψ(t) = [0.5et,−2et]T,t ∈[−0.2,0]。成本函数(6)的加权矩阵为

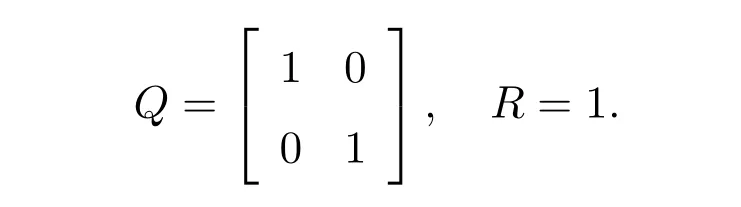
选取λ=0.25,α=0.4,β=0.5,µ=1.02。解线性矩阵不等式(57)∼(59)，可得

由(60)式，我们可得

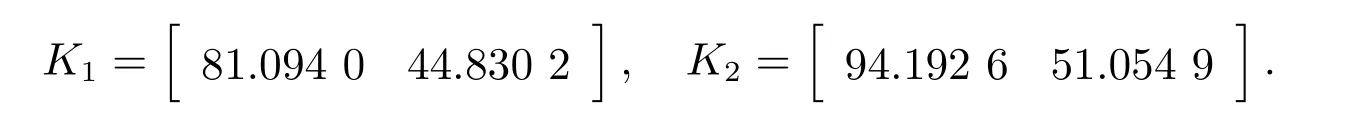
成本上界J∗=285.876 4。

根据(14)式计算，可得

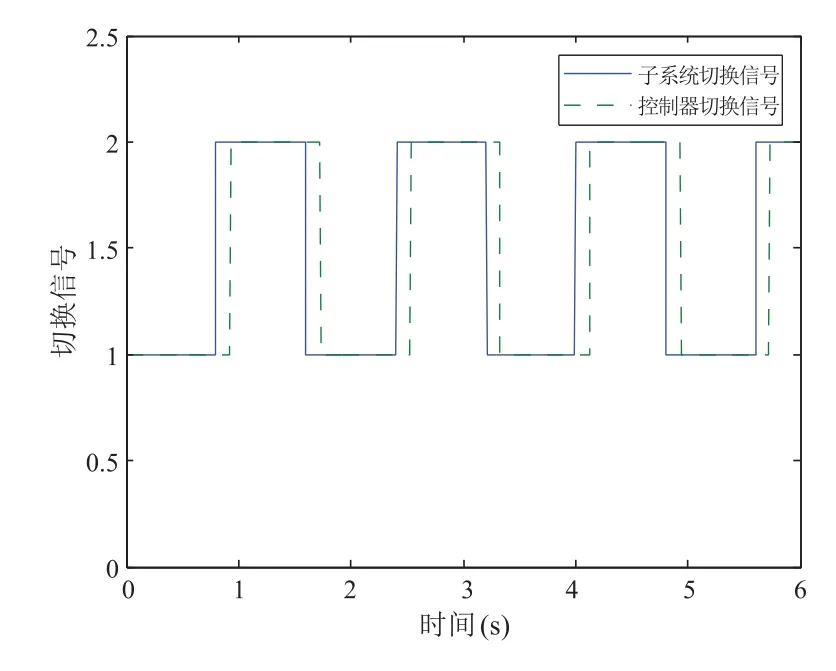
图1 切换信号

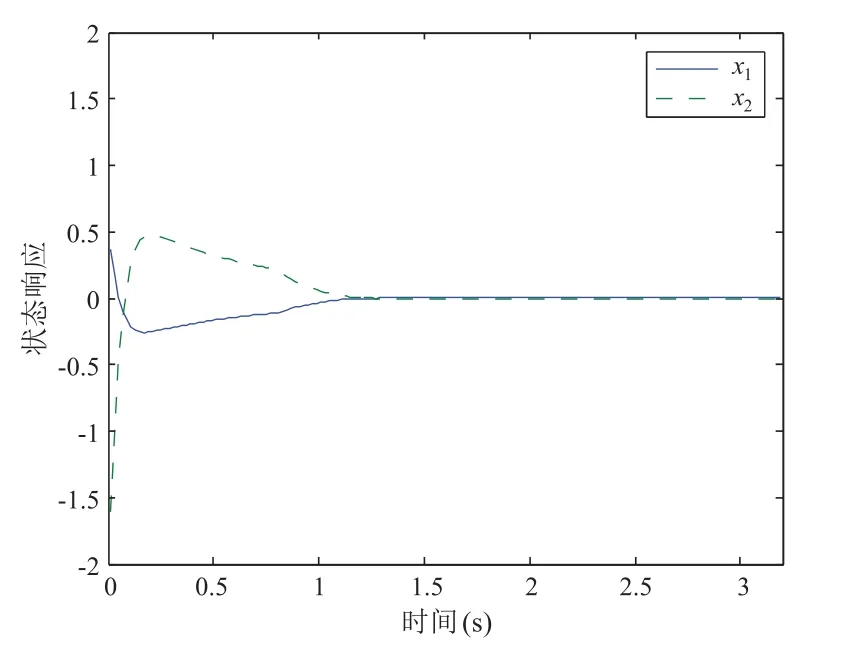
图2 闭环系统的状态响应

4 结论

本文研究了一类切换时变时滞系统在异步切换下的保成本控制问题。通过构造允许在异步阶段函数值增加的分段Lyapunov 函数，并使用平均驻留时间方法，给出了闭环系统指数稳定的一个充分条件和闭环系统成本函数的一个界。我们将保成本控制器的设计问题转化为求解一组线性矩阵不等式，给出了一个数值例子说明了结果的有效性。