高频直流脉冲下锂离子动力电池热特性实验
2022-09-29谢长君胡钟孝邦
陈 攀,黄 敏,谢长君,胡钟孝邦
(1.武汉理工大学自动化学院,湖北武汉 430070;2.岚图汽车科技公司,湖北武汉 430051)
锂离子动力电池因具有能量密度大、循环寿命长、低碳环保等优点被广泛地运用在交通储能等领域,然而其工作性能易受到自身温度的影响。低温会使锂离子动力电池各项性能指标严重下降,可用容量急剧减小,还会加速电池老化而导致寿命衰减[1-2]。而高温同样使锂离子动力电池性能降低和容量衰减,还容易诱发电池安全问题,严重时甚至引起电池燃烧爆炸[3]。
目前对电池在不同电流工况下的热特性已有较多研究。Ruan H J 等[4]研究发现,在恒定极化电压情况下存在最佳频率的交流电流可使锂电池快速发热升温,如施加1 377 Hz 交流电在338 s 内可使锂电池从-15.4 ℃升温到5.6 ℃。张志杰等[5]针对锂电池的温升特性进行了数学建模分析,结果表明,高倍率直流放电会引起电池温度快速升高,导致电池的温度超出其安全工作的温度上限,严重影响电池性能和使用寿命。Qu Z G 等[6]进一步在4.5C放电倍率下对电池进行2 Hz直流脉冲放电研究,发现电池的温升速率可达6.74 ℃/min,且发现相比恒定直流放电,低频的脉冲放电对电池健康状态的影响较小。Shang Y L 等[7]发现在高频交流电激励下,电池内部产热量与频率正相关,且电流激励频率越高,电池温升越快。同时Shang Y L 等[8]在研究电池超高频脉冲放电时,发现高频脉冲电流也能够加快电池的发热,但仅讨论了50 和150 kHz 两个频率,对其他频率未做分析。Chen L R 等[9]更加详细地研究了1 Hz~10 kHz 频率段的直流脉冲放电,发现在最小交流阻抗所对应的1 055 Hz 频率下电池的发热量最小,但并未指出直流放电频率与电池发热量的具体关系,且没有探究更高的放电频率。这些文献充分研究了锂离子动力电池在不同类型电流和不同频率下的热特性,但对于电池在高频下的生热特性研究还不全面,对锂离子动力电池在高频下的生热模型拥有不同看法和公式表达[5-9]。
在实际工程应用中,锂离子动力电池通常与电力开关器件相连接,这些器件的通断会在电池回路引起高频的电流谐波,从而使电池温度升高,影响电池的工作性能。因此探究锂离子动力电池在高频下的生热特性有利于电池的热管理,可同时为冬季电池加热研究和夏季电池散热研究提供新的思路。本文设计了基于全控器件的放电电路,利用电池自放电产生高频脉冲电流,并基于Bernardi产热方程建立电池生热模型,探究锂离子电池在不同高频直流脉冲下的生热特性。
1 实验平台设计
电池放电实验平台如图1 所示,由被测电池组、高低温实验箱、集成电路板、计算机及测温仪等检测仪器组成。实验前设置好实验箱的温度,然后将电池在恒温箱中放置4 h 使电池电芯温度与恒温箱温度一致,电池放电回路其他器件则放置在恒温箱外部。电池温度通过红外测温仪Fluke TiS75来检测,该设备具有-20~550 ℃量程,测量精度可达0.01 ℃。实验开始前将红外测温仪放入恒温箱中,将镜头对准单节锂电池圆柱表面,红外测温仪自动测量并计算电池表面温度的平均值,并实时记录保存。利用计算机屏幕可以实时查看电池表面温度,当电池到达指定的温度或者放电时间到达设定值时停止实验。

图1 高频直流脉冲放电实验平台
图2 为电池放电电路示意图,电路结构简单,电路通断采用lnfineon 公司的650 V CoolSiC 高性能MOSFET(型号为IMZA65R048M1H),该MOSFET 可稳定工作在150 kHz 开关频率下。功率电阻用于限制电流幅值,防止电流过大损坏电池。实验过程中,保持占空比为50%,使用霍尔电流探头采集电池放电电流,同时利用双路探针采集电池组端电压,数据均由示波器显示。

图2 高频直流脉冲产生电路
实验对象为市面上常见的18650 锂离子动力电池,该锂电池正极采用三元材料,电池质量为47 g,标称电压为3.7 V,额定容量为2 900 mAh,比热容为1.050 J/(g·℃)。
实验中使用电池组,由四节电池串联组成1 组,电池组的端电压为16.5 V。
2 电路工作原理与生热等效模型
2.1 实验电路等效模型
图3 给出了实验放电电路等效模型,电池采用Rint 模型,由一个理想电压源与内阻串联构成。由于高频下电流在电池内部产生的电压降落主要由欧姆内阻导致,极小部分是由极化内阻导致,两种内阻共同引起电压降落,因此本文将其合并称为电池内阻[9]。图3 中:UOCV为电池组的开路电压;Rn为电池组的总内阻;Ls为电流回路中存在的寄生电感;RΩ为功率电阻,Rw为电路中导线电阻和接触电阻之和;CDS为MOSFET 的栅源极间电容;i(t)为流过电池的电流。电路工作在MOSFET 导通和关断两种模态。

图3 实验等效电路模型
(1)MOSFET 导通
当MOSFET 导通时,电路工作在图3(a)状态。由于电路中存在寄生电感,电池放电电流会逐渐上升,寄生电感在低频条件下对电流的约束可忽略,高频则有较大影响。在此模态下有:
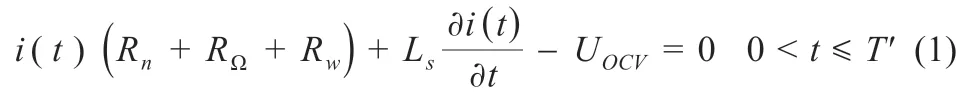
当一个周期开始时电流的初值i(0+)=a时,解微分方程可得:

式中:Rz=Rn+RΩ+Rw,为电路的总电阻;T'为一个周期内MOSFET 开启的时间。
(2)MOSFET 关断
当MOSFET 关断时,电路工作在图3(b)状态。由于线路的电流不能突变,同时MOSFET 存在漏源极电容CDS和线路寄生电感,电感上的能量将迅速转移到电容,形成衰减的电流,直致电流完全减小到零,在此模态下有:


式中:UR为电路电阻压降;UC为MOSFET 栅源极间电容压降;UL为寄生电感压降。
回路电流在MOSFET 关断瞬间具有初值i(T’+)=b,同时栅源极间电容电压UC(T’+)=0,于是联立方程(3)~(7),再引入拉普拉斯变换算子可列方程:
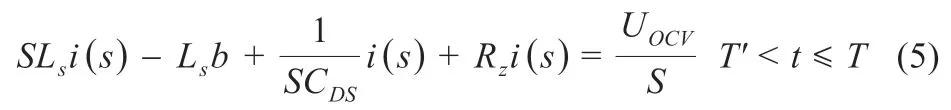
根据理论分析和实验条件可知本次实验中有:

综合求解方程(5)可得:

综上,一个开关周期内电池组的放电电流可以由式(2)和式(7)两部分表示。同时根据式(7)和仿真结果可知,衰减的电流为振荡电流,在低频时振荡电流持续时间极少,对回路电流各项数值的影响可以忽略,但高频时则有较大影响,且频率越高影响越大。电路的仿真电流波形见图4。

图4 仿真电流波形
2.2 电池热模型
在常用的锂离子动力电池热模型中,Bernardi 模型具有简单直观、参数容易获取的优点[10]。本文基于该模型开展电池温升仿真分析。研究表明,18650 型电池温度分布均匀,放电过程中内部温度和表面温度几乎相同[11]。故电池的产热及升温模型为:

式中:Qc为电池的产热功率,忽略放电过程中的其他产热量,由电池可逆热和电池焦耳热组成;Qs为电池的散热功率,表示电池与环境之间的热量传递;m为电池质量;cp为电池的比热容;h为对流换热系数;S为电池的表面积;Tcell为电池温度;Troom为电池所处环境温度。
由方程(10)可得,放电时电池温度表达式为:

停止放电后电池温度表达式为:

式中:T0为电池降温开始时的电池温度。
研究表明在电池升温过程中,∂UOCV/∂T通常是负值,且变化较小,一般可认为是常量[12]。由式(10)可知:反应热与电流的方向有关,与电流的算数平均值呈正相关;焦耳热与电流的平方和电池的内阻呈正相关。因此在电池内阻条件一定的情况下,增加电流有效值和电流的算数平均值可以提高电池发热量,提高温升速度。
2.3 实验电路等效参数辨识
实验检测电池组放电停止后电池表面的降温曲线,再通过方程(12)拟合参数可以得到电池组在实验温度环境下的对流换热系数h。
实验中放电电流限定在了较小范围内,同时电池升温幅度较小,可以观察到电池的电流波形和电池端电压降落在加热过程中基本无变化。因此选取电池放电稳定后的N个电流周期,通过锂电池外电路电压的降落和电流的增加估算求出电池组的内阻[6],计算方程如下:
式中:Δux为某个周期的端电压降落,Δix为这个周期的电流增加量。
根据实验获取的电流曲线可以求取电流的有效值和算数平均值,再结合公式(2)拟合近似求得电路的寄生电感Ls。

3 实验结果
实验所用锂离子电池组的荷电状态(SOC)为1,首先在室温11.3 ℃(初春天气状况良好条件下的室内温度)实验条件下,选取开关频率10、30、50、70、90 kHz 进行实验,实验时间为300 s。图5 为室温下实验电池组的温升曲线对比,详细温升速率见表1,从图表中可以看出,在高频10 kHz 后,随着开关频率不断增加,锂电池的温升速率逐渐减小,90 kHz 的温升速率仅有10 kHz 的29%,且在相同的50 kHz 频率下,将放电电流幅值提高66%,电池温升速率增加了160%,实验结果表明减小电池脉冲放电频率和增加电流幅值均可以显著提高电池生热速率。

图5 11.3 ℃条件下电池的温升曲线

表1 不同频率温升速率对比
为进一步探究电池生热特性与开关频率的关系,设计在0 ℃(选取开关频率1、5、10、50、70 kHz)的条件下进行实验,当温度上升至5 ℃或实验时间达到700 s 时停止实验。
表2 和图6 给出了根据2.3 节求取的0 ℃实验中的各项参数以及它们的变化规律。拟合的实验结果表明不同开关频率下电路的寄生电感基本相同,且电池的压降内阻规律符合电化学交流阻抗频谱(EIS)测量的规律[7],即从低频到高频,电池等效内阻先下降再上升。

表2 实验参数

图6 实验参数变化趋势
图7 所示为环境温度0 ℃条件下的电池温升曲线。实验结果显示,电池的温升速率与放电频率呈负相关,即电池放电频率越高,电池的发热量越小。图8 给出了电池在不同频率下的放电曲线,观察图8 中电流可知,在线路电感和开关电容影响下,高频开关会改变电池的放电电流曲线,导致电流由方波逐渐改变成三角波,同时电流振荡还产生较大的反向电流。再结合图6 中各项参数的变化趋势可知,电流曲线的变化使电流的有效值减弱,同时还大幅减小了电流的平均值。由式(10)中的电池生热模型得知,电池的发热量与流过电流的有效值、平均值以及电池内阻呈正相关,虽然实验中电池的内阻在高频时略有增加,但电流的减小仍然导致了高频下电池发热量变小。图9 给出了仿真温度和实测温度的对比,可以看到经由电池电热模型得到的温升曲线与实际实验所得温升曲线高度吻合,温度差异不超过0.15 ℃,相对误差不超过7%,验证了本文所用电池热模型具有较高的准确性。
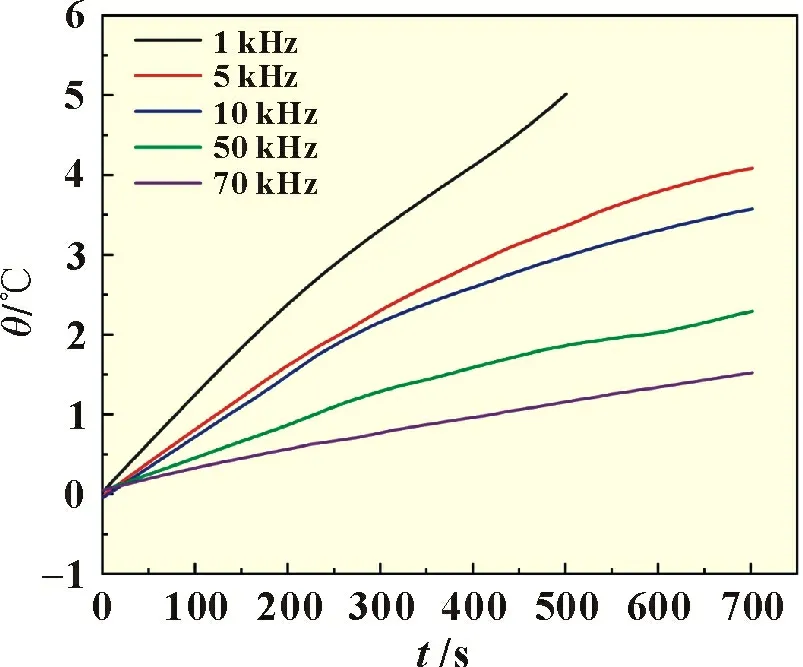
图7 0 ℃条件下电池的温升曲线

图8 不同频率的实际电流曲线

图9 实测与仿真温度曲线
4 结论
本文探究了高频直流脉冲激励下的锂电池发热特性,搭建简易的实验平台完成了两种不同温度条件下的电池高频直流放电实验。对实验涉及的电参数和热物性参数进行了估算和拟合,采用Bernardi 电池热模型进行仿真模拟并与实验温升曲线作对比,得出以下结论:
(1)锂离子电池在高频直流脉冲放电情况下的产热量与流经电池的电流的有效值和平均值大小呈正相关,电流越大升温越快;
(2)本实验拓扑下电流脉冲有效值和平均值会随着频率升高而减小,进而减小电池发热速率;
(3)在保持电流有效值不变的情况下,电池产热率会随频率不同而发生变化,初步判断其原因是电池内阻随着频率不同而有变化,导致高频脉冲流过电池时电流在电池内部产生的焦耳热发生变化;
(4)根据热力学第一定律推导出的Bernardi 电池生热率模型适用于高频直流脉冲工况下的电池产热率分析,可以用于研究直流脉冲工况下锂离子动力电池的热特性及热管理。
