浅谈梯度与等高线的关系

白冬梅

（中国矿业大学 数学学院 江苏徐州 221116）

一、问题的提出

高等数学的梯度问题教学过程中，经常有学生提出诸如等高线和梯度有什么关系，梯度和方向导数有什么关系等问题。要回答这些问题，需要先理解一元函数的导数和多元函数的偏导数及方向导数等概念。

对于一元函数，自变量只有一个，当x近于x0时，x只能沿直线变动，移动的方向只有左右两个方向。从几何角度，一元函数表示二维平面上的一条曲线，曲线上某一点（x0，y0）处切线的方向有两个，自变量由小变大时，函数值增大的趋势用导数描述；自变量由大变小时，函数值增大的趋势由负导数值描述。而对于多元函数，以二元函数为例，自变量有两个，表示自变量的点（x，y）趋近于（x0，y0）时，不仅可以移动距离，而且可以按任意的方向来移动同一段距离。因此，函数的变化不仅与移动的距离有关，而且与移动的方向有关。而从几何角度，一个二元函数表示三维空间中的一张曲面，曲面上从某一点（x0，y0，z0）处的切线的方向有无穷多个，自变量沿不同切线方向变化时函数值变化的趋势则由方向导数描述。

下面我们从方向导数和梯度的概念出发，结合等高线的概念阐述它们之间的联系。

二、方向导数，梯度

方向导数的计算公式[1]：如果函数f（x，y）在点P0（x0，y0）可微分，那么函数在该点沿任一方向l的方向导数存在。

其中cosα，cosβ是方向l的方向余弦。

方向导数是一个数，反映的是f（x，y）在P0（x0，y0）点沿方向l的变化率。方向导数为正，说明函数在该方向上递增；方向导数为负，说明函数在该方向上递减。

梯度[1]：设函数f（x，y）在平面区域D内具有一阶连续偏导数，则对于每一点，都可定出一个向量这个向量称为函数f（x，y）在点P0（x0，y0）的梯度，记作grad f（x0，y0）。

等高线[1]：在xoy平面上，曲线f（x，y）=C称为函数z=f（x，y）的一条等高线.即取不同C值，在空间坐标系中用平面z=C去截曲面z=f（x，y），将截得的空间曲线投影到xoy平面上既得曲面z=f（x，y）的一条等高线。

三、方向导数与梯度、等高线的关系

将函数f（x，y）在点P0（x0，y0）处的梯度及沿方向l的方向导数联系起来。定义与方向l同方向的单位向量el=（cosα，cosβ），再利用向量内积的计算公式可得

其中γ为P0（x0，y0）处梯度方向与方向l的夹角。

由（1）式可见方向导数的大小既与梯度的模有关又与γ的大小有关。

若l与梯度的方向相同，即γ=0，cosγ=1

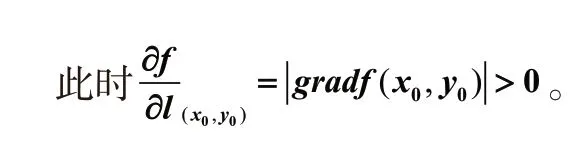
也就是说函数在梯度方向的变化率是正的，且此方向的方向导数值最大，所以函数值沿该方向（梯度方向）逐渐增大且增大的速度最快，从而在梯度方向上函数值由小变大，即梯度方向由函数的低等高线指向高等高线。

以下我们讨论等高线上点的切线方向与该点的梯度方向有什么关系？

由以上梯度的定义可知，函数z=f（x，y）在点P0（x0，y0）的梯度向量为：

则梯度向量斜率（即梯度相应于x轴正方向的倾角的正切值）为：

而等高线f（x，y）=C在点P0（x0，y0）处的切线斜率（即切线相应于 x轴正方向的倾角的正切值）为：

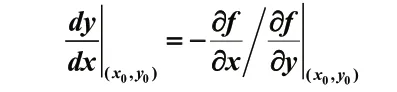
从而得到，在点P0（x0，y0）处的梯度向量的斜率与该点处等高线的切线斜率乘积为-1，综上所述，梯度方向与等高线的法线方向一致，即梯度方向与等高线的切线垂直。

图2 曲面 z =4-x 2 -y2对应于截面z=3，z=2的两条等高线平面图

四、举例

我们通过高等数学中的典型函数为例，从方向导数，梯度，等高线的概念出发分析它们的用法。

例1

分析

在点（1，-1，1）处的梯度已知，那么函数u在（1，-1，1）处的三个偏导数就已知

例2

用Matlab软件做出函数z=xy的曲面图及等高线图，并分析等高线与梯度的关系。

分析：从图3可以直观看出曲面为一个马鞍面，在[-10，10]*[-10，10]上，该曲面一组对角上翘，一组对角下折。该曲面的等高线图如图4。

图3 函数z =xy 曲面图

图4 曲面z=xy的等高线和梯度方向图

讨论：图4中实线为函数z=xy的等高线，箭头代表梯度的方向。箭头越长的地点梯度越大，箭头所指方向为函数值增大的方向，即曲面上高度增加的方向；且等高线越密集的区域，高度变化越快，反映出曲面坡度的缓陡：等高线稀疏的地方表示缓坡，密集的地方表示陡坡，间隔相等的地方表示均匀坡；两对等高线凸侧互相对称时，曲面上表现为“马鞍”形状，故形象地称为鞍部，曲面也常被称为“马鞍面”。

结语

本文分析了梯度、方向导数和等高线等概念之间的关系，并利用Matlab绘制了具体函数的等高线图进行辅助教学，增强教学内容直观性，加强学生概念理解与记忆，同时强化理论基础与数值编程结合应用。