FNOD:基于近邻差波动因子的离群点检测算法①

张忠平 邓禹 刘伟雄 张玉停

（∗燕山大学信息科学与工程学院 秦皇岛066004）

（∗∗河北省计算机虚拟技术与系统集成重点实验室 秦皇岛066004）

（∗∗∗河北省软件工程重点实验室 秦皇岛066004）

0 引言

离群点是数据集中偏离大部分数据的数据,由于偏离其他数据太多,这些数据的偏离可能并非由随机因素产生,而是产生于完全不同的机制[1]。离群点检测是一个长期存在于数据挖掘领域的基本主题,其旨在消除噪音和干扰或发现潜在的、有价值的信息。离群点检测在欺诈检测[2]、垃圾邮件检测[3]、交通异常检测[4]、入侵检测[5-6]、医疗与公共卫生安全监测[7]等领域有着广阔的应用前景。

目前,国内外许多学者在离群点检测领域的研究十分活跃,提出了大量优秀的离群点检测方法,这些方法大致可分为基于分布的、基于距离的、基于密度的、基于聚类的和基于深度的5种[8]。近年来也有一些新方法被提出,文献[9]和文献[10]通过构建k 近邻（k nearest neighbors,KNN）图,利用图的标签传播和随机游走的方法检测离群点。

早期基于分布的方法通过判断数据点偏离正常分布模式的程度判断离群点[11],但该方法不适用于高维数据集,特别是数据集数据分布未知的情况。

为了改进基于分布方法的缺陷,文献[12]提出了一种基于距离的离群点检测方法。该方法通过计算数据点到其k 近邻点的平均距离,选取平均距离最大的n个点作为离群点,但由于该方法使用的是全局阈值,未考虑局部环境的影响,因此难以检测局部离群点。

为解决基于距离方法的问题,文献[13]定义了局部离群因子（local outlier factor,LOF）算法,该方法将数据点与其k 近邻点平均距离的倒数看作局部密度因子,密度因子越小,该点是离群点的概率越高。LOF 算法作为经典的局部离群点检测算法已被广泛研究,但存在精确度较低、参数敏感等问题,很多研究学者都对此算法提出了改进。INFLO（influence outlierness）算法[14]、NOF（natural outlier factor）算法[15]分别在局部密度因子中引入了反向k 近邻（reverse k nearest neighborhood,RNN）和相互k 近邻（mutal k neighborhood,MUN）提高了算法的性能。RDOS（reverse shared outlier density）算法[16]将局部密度因子替换为效果更好的核密度,同时引入反向k 近邻、相互k 近邻和共享k 近邻提高了检测精度。文献[17]提出的DDPOS（density and distance parameters outlier factor scores）算法利用反向k 近邻来排除掉部分边界点的干扰,类似的算法还有RDOF（relative density outlier factor）[18]和LCDO（local correlation dimension outlier）[19]。

文献[20]引入反向近邻关系,提出了一种将k近邻点和反向k 近邻点数的比值作为离群因子的快速离群点检测方法。文献[21]提出了一种基于不稳定因子的离群点检测方法INS（INStability factor）,通过计算虚拟k 近邻点的稳定性判断离群点。以上方法都需要遍历数据集中所有点,然后再对离群因子进行排序来确定离群点,但是此类方法对计算位于聚类区域的正常点是没有必要的。

为解决上述问题,文献[22]通过DBSCAN（density-based spatial clustering of applications with noise）聚类的方法剪枝位于聚类中心的正常点,只计算保留下的可疑点,减少了后续离群点检测算法的计算量。文献[23]提出了一种基于累积权熵空间聚类（subspace outlier detection cumulative holoentropy,SODCH）的离群点检测算法,利用k-means 对子空间进行聚类,根据累积权熵检测离群点,大幅提高了算法处理数据的力度。文献[24]利用相互k 近邻关系提出了一种无参数的聚类方法,减少了算法对参数k的依赖。文献[25]提出了一种基于聚类因子和相互密度的离群点检测算法,通过引入相互k 近邻关系提高了算法的精确度。

通过对上述算法的总结可以看出,很多改进算法都在原有的离群因子中引入了更复杂的近邻关系,但没有改变离群因子的计算方法,且未考虑变化的参数k对离群点检测的影响。随着数据分布越来越复杂,这些离群点检测算法效果不够理想,因此,本文提出一种基于变化参数k的离群因子,为离群点检测提供了新的研究方向。基于聚类的剪枝方法对数据聚类程度要求较高,不能适应多种数据集,因此提出一种新的剪枝方法,也是一个新的研究方向。综上所述,本文引入相互k 近邻关系,提出了一种基于近邻差波动因子的离群点检测算法（outlier detection algorithm based on fluctuation of nearest neighbor difference factor,FNOD）。该算法引入相互k 近邻关系,首先提出一种近邻剪枝算法（neighbor pruning factor algorithm,NPF）剪枝正常点,保留离群度较高的可疑点,降低运算量,提升后续离群点检测算法的精确度;其次设计迭代减小的参数k,随着k值减小,离群点的相互k 近邻变化程度要小于正常点;最后利用数据点相互k 近邻变化的波动程度刻画每个点的离群程度。

本文其余部分安排如下。第1 节介绍相关工作,关于相关算法的各种定义。第2 节对本文提出的算法进行阐述。第3 节通过实验对所提算法的实效性进行验证。第4 节对本文做出总结。

1 相关工作

下面简要介绍相互k 近邻数搜索算法。

1.1 相关定义

定义1k 距离（k_distance）[15]。数据点p的k距离表示点p和其第k个近邻点o之间的欧氏距离,用k_dist（p）表示。点p至多存在（k-1）个o′点满足dist（p,o′）≤dist（p,o）。

定义2k 近邻[15]。点p把点q看作k近邻点。数据点p的k近邻集合表示为KNN（p）⊆D,要求点q满足dist（p,q）≤k_dist（p）,定义为式（1）。

其中,D表示数据集,p、q、o为数据集D中的数据点,dist（p,q）表示点p、q之间的欧式距离,k为正整数。

定义3反向k 近邻[15]。数据点p被点q看作k 近邻点,数据点p的反向k 近邻集合用RNN（p）⊆D表示,定义为式（2）。

定义4相互k 近邻。数据点p的相互k 近邻用MUN（p）⊆D表示,要求在当前k值下,点p是点q的k 近邻,同时点p也是点q的反向k 近邻,定义为式（3）。

相互k 近邻建立在k 近邻的基础上,要求两点互相将对方看作k 近邻,受距离和参数k的影响,当一个点距离其他点越远时,其越不容易被其他点选为k 近邻点,也就很难形成相互k 近邻关系。图1中单向箭头表示k 近邻,双向箭头表示相互k 近邻。k=1 时,点q是点p的k 近邻,由于点q与点o的距离小于点q与点p的距离,所以点q的k 近邻是点o,同理点o的k 近邻点是点q,因此点q与点o形成相互近邻关系,未与点p形成相互近邻关系。若使点p与点o和q形成相互近邻关系,只有扩大参数k值,使点p成为点q和o的k 近邻点。如图1（b）中k=2 时所示,点p成为点o和q的第2个k近邻点,此时点p形成了相互k近邻关系,所以相互k 近邻关系受到距离和参数k的影响。

图1 相互k 近邻关系

图2 显示了不同k值下,数据点相互k 近邻的变化情况。图中虚线单向箭头代表k 近邻关系,双向箭头代表相互k 近邻关系（点o和r存在一条双向箭头）,点p为离群点。

图2 参数k 变化对相互k 近邻关系的影响

由于图中离群点p远离其他点,且参数k较小,所以点[o,s,r] 是点p的k 近邻点,但点p不是点[o,s,r] 的k 近邻点,因此点[o,s,r] 不会与点p形成相互近邻关系。k=4 时点p仅与点q形成了相互近邻关系,而其他点均有3 或4 个相互k 近邻点。

表1 统计了图2 中不同参数k下,部分数据点相互k 近邻点的变化。当参数k递减时,数据点的k 近邻点减少,所以数据点的相互k 近邻点也会减少,相互近邻点开始发生变化。由于离群点p仅有一个相互k 近邻点,因此随着参数k下降,最多发生一次相互k 近邻变化。但位于聚类区域的点[q,o,s],由于其相互k 近邻点个数接近k 近邻点个数,伴随k值下降,这些点会有多次相互k 近邻变化。

根据图2 和表1 的描述可以总结出:（1）在某一参数k下,离群点的相互k 近邻点个数要小于k近邻点个数;（2）在变化的近邻参数k下,离群点的相互k 近邻点数相对稳定,不易发生变化。本文根据（1）设计一种基于相互k 近邻关系的近邻剪枝方法,排除正常点;根据（2）设计一种在变化参数k下基于数据点相互k 近邻波动的离群点检测算法。

表1 数据点相互k 近邻点个数

1.2 相互k 近邻数统计算法

根据1.1 节描述的相关定义,统计相互k 近邻数量的算法如算法1 所示,首先根据输入的近邻参数k计算每个点的k 近邻和反k 近邻;再根据相互k 近邻的定义,搜索每个数据点的相互k 近邻;最后统计每个数据点的相互k 近邻的数量作为输出。

在相互近邻数搜索（MUNn-Searching）算法中,KNN（i）代表数据点i的k 近邻点集合,RNN（i）代表数据点i的反向k近邻集合,MUN（i）代表数据点i的相互k近邻点集合。MUNn-Searching 算法的时间复杂度源于利用KD 树计算k 近邻点的过程,时间复杂度为O（n·logn）,n为数据集中数据点的个数。

2 近邻差波动算法

2.1 近邻剪枝算法思想

离群点检测算法中对聚类区域中正常点的计算是没有必要的,为减少此类点的计算,本文利用相互k 近邻提出了一种近邻剪枝算法,能够剪枝大部分聚类区域的正常点,减少后续离群点检测算法的计算量。

根据定义2 k 近邻、定义4 相互k 近邻和图2可知,由于离群的数据点距离聚类区域的数据点较远,难以被聚类区域的点看作k 近邻点,因此相互k 近邻点的数量远远小于k 近邻点数量,反之位于聚类区域点的相互k 近邻点数量接近k 近邻点数量。因此,聚类区域点的k 近邻点数与相互k 近邻点数的比值接近1,稀疏区域点的k 近邻点数与相互k 近邻点数的比值远远大于1。据此特点可以使大部分正常点被剪枝。

定义5近邻剪枝因子（NPF）。NPF（p）是数据点p在某一k值下k 近邻个数和相互k 近邻点个数的比值,定义为式（4）。

式中,KNNn（p）表示数据点的k 近邻点个数,等于近邻参数k,MUNn（p）表示数据点p的相互k 近邻点个数。将分母MUNn（p）加1 是为了防止出现分母为0,即数据点p没有相互k 近邻点的特殊情况,分子KNNn（p）加1 是为了降低MUNn（p）加1 带来的影响。

2.2 近邻剪枝算法

根据2.1 节中描述及相关定义,近邻剪枝算法如算法2 所示,该算法首先根据输入的参数k统计数据点k 近邻点和相互k 近邻点个数,随后计算数据点的近邻剪枝因子NPF,最后对所有数据点按NPF 值降序排序,保留最大的前pt个数据点作为可疑点。

剪枝后保留的可疑点的相互近邻数很少,能够减少相互近邻随参数k变化而变化的次数,有利于提高基于近邻差波动的离群点检测算法精度。NPF算法的时间复杂度主要来源于利用KD 树计算k 近邻点的过程,时间复杂度为O（n·logn）,n为数据集中数据点的个数。相比基于聚类的剪枝算法[22],具有剪枝程度大、速度快的优点。

2.3 近邻差波动因子算法思想

本文提出了一种基于近邻差波动因子的离群点检测方法FNOD,算法思想源于相互k 近邻关系。聚类区域的点容易形成相互k 近邻,且相互k 近邻易随参数k减小而减少,相反,由于离群点远离聚类区域,相互k 近邻点很少,所以相互k 近邻不易随k值减小而减少。

图3 所示的数据集中,双向虚线代表相互k 近邻关系,A代表一个小聚类,点B为局部离群点,点C、D、E为全局离群点。虚线表示在当前k值下存在的相互k 近邻关系。对比发现在k=[10,9,…,2]过程中全局离群点C、D、E的相互k 近邻点不会变化;k=[1,2,…,5]过程中局部离群点B的相互k近邻点不会变化;聚类A中的点在k每次变化后都会发生变化。离群程度越高的点越不易发生相互近邻的变化,本文据此设置一个迭代减小的参数k,随着k值减小,数据点相互k 近邻点发生变化,离群程度越高的点,其相互k 近邻点数越少,甚至为0,不易变化。本文设计用波动的方式描述数据点相互近邻变化程度,波动越小的点是离群点的概率越大。

图3 FNOD 算法思想示意图

2.4 相关定义

本节详细介绍FNOD 算法及其相关定义,其中,D表示数据集;p代表数据集中的数据点;i代表参数k的迭代次数;ki代表第i次迭代 时的k值;MUNi（p）表示数据点p在第i次迭代时的相互k 近邻点个数;n为正整数表示初始k值。

定义6近邻差d（p）。di（p）是数据点p第i次迭代后相互k 近邻点数的差,用来描述相互k 近邻的变化程度,定义为式（5）。式中MUNi-1（p）和MUNi（p）分别为第i-1 和第i次参数k变化后,数据点p的相互k 近邻点个数。n为数据点个数,本文将一个di（p）看作一次波动。

定义7稳态ST（steady）。稳态表示数据点在相邻两次k值变化过程中近邻波动差di（p）=0 的状态。

本文定义ST=0,是因离群点的相互k 近邻点较少,因此在近邻参数k下降过程中,离群点的近邻差不容易发生变化,即di（p）=0,相反正常点会随着参数k的变化而变化。统计数据点在整个参数k值迭代过程中di（p）每次的变化情况是否贴近di（p）=0,因此设置整体稳态ST=0。

定义8近邻下降率α。参数k的下降速度定义为近邻下降率。定义为式（6）。

近邻下降率α直接决定算法迭代的次数,α值越大,k值减小的速度越快,算法迭代的次数越少,但会降低离群点检测的精确度。如图4 所示,k=3时点p的相互近邻点数为1;k=2 时,点p的相互k近邻点减少到0;k=1 时,点p的相互k 近邻点仍为0。因此k值从3 到2 形成了一次波动,从2 到1 是一个稳态。稳态有利于增加离群程度,而波动会降低离群程度。若参数k直接从3 降到1,会丢失一个稳态,降低离群程度,因此本文设置近邻下降率α=1。

图4 近邻下降率α 对稳态的影响

此外设置k=1 时停止迭代,此时每个数据点只 有1 个k 近邻点,每个数据点至多只有1 个相互k近邻点,减少相互k 近邻点数由1 到0 带来的必然波动。

定义9近邻差波动因子FNOD（p）描述数据点p随k值下降,点p的近邻波动差d（p）的变化情况,参考统计学中的标准差,定义为式（7）。

标准差描述的是各个阶段的数据相对均值的波动情况,本文中要求统计数据点相对于稳态的波动情况,因此,用稳态ST=0 替换均值。本文设置初始参数k,同时参数k按近邻下降率α=1 迭代,直到k=1,共迭代n-1 次。FNOD（p）波动值越小,说明此点是离群点的概率越高。

在图5 （a）所示的人工数据集中,验证了随着参数k减小,不同类型的点的近邻差波动不同。图中数据点A和B为正常点、C为离群点,它们的近邻差波动如图5（b）所示,图中横坐标轴为参数k,纵坐标轴为近邻波动差,根据近邻波动因子,定义ST=0 为横坐标轴。计算图中折线相对于横坐标轴的波动情况,可得FNOD（A）=0.95、FNOD（B）=1.0、FNOD（C）=0.46。点C的近邻波动因子远小于其余两点,因此点C为离群点。通过观察图5（b）也可以看出,离群点C的波动程度很小,只有4次d（p）=1 的波动,相反正常点B有18次d（p）=1,点A拥有多次d（p）=1和d（p）=2 的波动。

图5 正常数据和离群数据样本

2.5 FNOD 算法描述

本文提出的一种基于近邻差波动的离群点检测算法FNOD,输入数据集D和参数k,输出离群点。首先对数据集进行剪枝,排除位于聚类区域的正常点,留下可疑点;随后在迭代减小的参数k下,计算可疑点的近邻波动因子,按从小到大排序,前n个点即为离群点。FNOD 算法代码如算法3 所示。

算法3中Odoubt存放剪枝后保留的可疑点,MUN（pk）为当前k值下,数据点p的相互k 近邻点数,集合MUN（p）存放点p每次k值变化后的相互近邻数,集合FNOD（Odoubt）存放所有可疑点的近邻差波动因子,算法最终输出波动最小的前n个点作为离群点。FNOD 算法的时间复杂度主要来源于两方面:（1）使用KD 树寻找相互k 近邻点个数,时间复杂度为O（n·logn）,n为剪枝后可疑点个数;（2）参数k迭代减小,时间复杂度为O（k）。算法总体的时间复杂度为O（k·n·logn）。

3 实验评估

为检测FNOD 算法的性能,在人工数据集和真实数据集下进行实验,同时将FNOD 算法与较为流行的——利用其他近邻关系的LOF[13]、INFLO[14]、NOF[20]、NOF2[15]算法和同样迭代k值的INS[21]算法进行对比。FNOD 算法和INS 算法的k值分别对应初始k值和截止k值。实验环境如表2 所示,实验结果使用Python 进行可视化处理。

表2 实验环境

3.1 实验指标

在大多数实际应用中,相比大量存在的正常数据,含有异常值的数据显得非常稀有,数据分布存在极端不平衡现象。因此,常见的准确率等指标不能客观评价算法性能。为评估离群点检测的性能,针对人工数据集,采用精确率（precision,Pr）指标进行评估。精确率定义如式（8）所示。

式中,TP表示算法检测到的真实离群点数量,FP表示算法错误地将正常点判断为离群点的数量。精确率数值越大,算法性能越好。

针对真实数据集,采用F1 曲线和接受者操作特性曲线（receiver operating characteristic curve,ROC）的曲线下面积（area under curve,AUC）进行评估。F1 值是衡量二分类模型的一种常用指标,其同时兼顾了精确率和召回率两个指标。F1 值越接近1,算法性能越好。F1 值定义如式（9）所示。

ROC 是以真阳性率（TPR）为纵坐标,假阳性率（FPR）为横坐标绘制的曲线,ROC 曲线描绘了两者的相对权衡。真阳性率和假阳性率的定义如式（10）、（11）所示。AUC 可以直观地展现出算法的性能,值取0 到1 之间,越大的AUC 值意味着算法有更大的概率将离群点排在正常点之前,所以AUC 值越大越好,小于0.5 意味着算法不可用。

3.2 人工数据集

为测试本文算法在各种复杂数据分布下的性能,实验在图6 所示的6 种二维人工数据集Data_01～ Data_06 中进行,图6 中“o”代表离群点。每个数据集的属性特征如表3 所示。

图6 6 种人工数据集分布

表3 人工数据集特征

图7 展示了本文FNOD 算法和其余5 个算法在6 个人工数据集上精确率随k值变化的过程,横坐标为k值,纵坐标为精确率Pr。

图7 人工数据集下不同算法的精确率变化曲线

随着参数k不断增大,FNOD 算法的精准率不断上升,最终大于或等于其余算法。特别是在Data_01、Data_05、Data_06 中,FNOD 算法的峰值超出了其余算法的峰值,分别达到0.95、0.98、0.86。此外FNOD 算法在Data_02、Data_03、Data_06 数据集中,曲线变化程度接近且高于同样使用相互k近邻关系的NOF2 算法。随着k值不断增大,实验中所有算法的精确率有所下降,但本文FNOD 算法的下降程度要低于其余算法,特别是在Data_01 数据集中初始参数k从150 增加到300 的过程中LOF、INFLO、NOF 和NOF2 的下降率分别为0.05、0.11、0.07 和0.10,而FNOD 的下降率为0.04,这是因为随着参数k增大,利用距离或密度的方法会不断获取一个较远的近邻点,这些方法依赖k 近邻点的距离计算离群因子,因此不断加入距离较大的k 近邻点不利于算法的精确度,而本文FNOD 算法用数量计算离群程度,受到的影响较小。

由于INS 算法相比于其余算法需要更大的k值,所以图7 中没有体现INS 算法的最佳精确率,将INS 算法的最佳精确率放置在表4 中。

表4 人工数据集精确率

通过总结图7 和表4 的数据,FNOD 算法在Data_02、Data_01、Data_03、Data_06 表现最优,Data_04 和Data_05 数据集中数据聚类不明显,所以表现略低于NOF2 算法。由于FNOD 算法需要统计多次参数k变化下的数据,当初始k值取到10 和20时,算法只能获得9 和19 次的波动数据,因此FNOD 算法在初始k值较小的情况下精确率较低。随着初始k值增加,FNOD 算法获取波动的数据增多,算法的精确度提高。

3.3 真实数据集

为较为全面地检测FNOD算法的真实性能,本文实验选择在6 个真实数据集Ecoli、Lonoshpere、Lymphography、PenDigits、Stamps 和Wdbc 中进行,6个真实数据集均来自UCI 数据库,表5 展示了真实数据集的数据特征。

表5 真实数据集特征

表6 展示了真实数据集下FNOD 算法和其余5个算法的AUC 值,同时标注出每个数据集中排名前2 的算法。FNOD 算法在每个真实数据集上的AUC值均属于表现最优的前2 个算法。特别是在Ecoli和PenDigits 中,FNOD 的AUC 值达到了0.96,超过同样使用相互近邻关系的NOF2 算法的0.91 和使用变化k值的INS 算法的0.78。在数据量较大的PenDigits 和离群点数较多的Lonoshpere 中,FNOD算法同样保持了较好的检测效果。面对维数较高的数据集Lymphography 时,FNOD 算法表现不佳,仅为0.80,但也接近其余几种算法的最佳值。整体上看FNOD 算法AUC 值大于同样使用相互k近邻的NOF2 算法。

表6 真实数据集AUC值

图8 展示了各个算法F1 值随参数k变化的曲线。通过观察图像可以得到,在各个数据集中,除在PenDigits 和Stamps 下的INS 算法F1 值为0.5,其余每个算法在各个数据集下的F1 曲线都接近一条逐渐上升的拟合曲线,表明各算法都具备一定的二分类效果。

图8 真实数据集下不同算法的F1 值变化曲线

真实数据集中,FNOD 算法在初始参数k较小时性能要低于其余5 种算法。随着k值增大,FNOD算法的F1 值逐渐上升,最佳F1 值大于或等于其余算法。由于Ecoli 数据集和数据集Lymphography 中数据数量较少,较大的初始参数k会接近数据点数量,从而导致数据集中离群点拥有较多的相互k 近邻点,不利于本文算法,所以FNOD 算法仅接近或略高于其余算法。Stamps 数据集中FNOD 算法的F1峰值达到了1,超出了NOF2 算法的0.91 和LOF 算法的0.92。在Lonoshpere 数据集中,FNOD 算法和LOF、INFLO、NOF 的指标均在0.82 上下波动。FNOD 算法优于同样使用相互近邻关系的NOF2 算法和利用参数k迭代的INS 算法。综合上述2 个指标,相较于其他算法,FNOD 算法在检测性能上有不同程度的优势。实验验证了本文算法能全面准确地检测到离群点。

3.4 检测效率对比

为对比FNOD 算法和其余算法的离群点检测效率,本节统计了各算法在人工数据集和真实数据集上达到最高检测精度的时间消耗,同时标注出每个数据集中排名前2 的算法,如表7 和表8 所示,表中单位为秒。

表7、表8 显示了各算法在不同数据集下的时间消耗。本文的FNOD 算法在大部分数据集中都属于排名前2 的算法,特别是在Data_06 和PenDigits中,算法的时间消耗为9.36 s 和5.35 s,远低于其余算法。本文的FNOD 算法和INS 算法都需要计算不同k值下的近邻信息,算法时间消耗较大,但由于FNOD 算法利用NPF 算法对数据集进行了剪枝,很大程度上减少了算法关于正常点的计算,从而减少了时间消耗,所以FNOD 算法的时间消耗远低于INS 算法。此外,由于Data_02 和Ecoli 数据集中数据分布较为分散,NPF 算法能够剪枝的正常点较少,导致FNOD 算法的时间消耗较大。综上所述,结合图7、图8 的实验结果,可以看出FNOD 算法以较低的时间消耗保持了较高的算法性能。

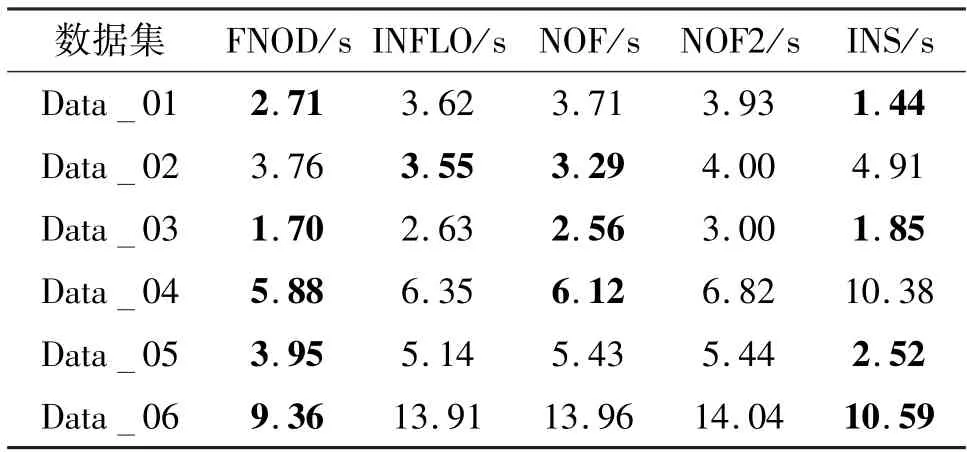
表7 人工数据集时间消耗

表8 真实数据集时间消耗

4 结论

本文分析了基于各种近邻关系的离群点检测算法和近年来较为新颖的算法。针对传统算法精确度较低且局限于获取一个参数k下的离群信息的问题,首先提出了一种基于相互k 近邻关系的近邻剪枝方法,排除大部分位于聚类区域的正常点,减少了关于正常点的冗余计算,同时提高了FNOD 算法的精确度;其次,提出了一种基于相互近邻波动的离群点检测算法,统计不同参数k下数据点的近邻差,根据这种差值的波动作为离群因子检测离群点。在人工数据集和真实数据集下的实验验证了该算法具有良好的离群点检测能力。但算法对初始参数k的选取也较为敏感,如何自适应获取初始参数k、减少算法对参数的依赖从而提高精确率,将是未来的研究方向。