具有死区输入的非参数不确定系统误差跟踪迭代学习控制①
2022-09-28陈凯杰施卉辉陈强
陈凯杰 施卉辉 陈强
(浙江工业大学信息工程学院 杭州310023)
0 引言
迭代学习控制(iterative learning control,ILC)对于有限区间内的重复跟踪问题有着良好的控制性能。早期的迭代学习控制方法主要包括P 型、D 型等学习算法[1-3],利用压缩映射进行收敛性分析,但往往要求满足全局Lipschitz 条件。基于Lyapunov-Like 的迭代学习控制算法[4-6]引起了大家的关注,该方法不但不受全局Lipschitz 条件限制,并且能更充分地利用已知系统信息。
传统ILC 方法往往要求系统满足初值一致条件[7-8],即系统状态初值与期望轨迹初值严格一致。但是,在系统实际运行过程中,由于建模的不确定性、环境因素影响和机械精度不足等原因,系统初值一致条件不能被满足。文献[9]利用状态初值设计误差函数和时变边界层函数,并利用时变边界层的衰减特性,实现系统误差的渐近收敛。文献[10]讨论了ILC 中的5 种初值情况并提出了修正期望轨迹方法,利用系统初值和期望轨迹设置过渡轨迹,保证系统初值与修正后的期望轨迹初值一致。文献[11]提出了误差跟踪方法,通过设计期望误差轨迹和迭代学习控制器,保证误差轨迹沿预设的期望误差轨迹收敛。误差跟踪方法避免了对期望轨迹的依赖,当期望轨迹发生变化时,期望误差轨迹的形式不发生改变。此外,对于接入点的位置和导数可以简单设置为0,减小了计算量。文献[12]利用定积分的起始点为0 的特点,构造了积分形式的期望误差轨迹。文献[13]把误差跟踪方法推广到更加一般的非线性严格反馈系统,使得系统误差沿着预设的误差期望轨迹收敛到零附近一个很小的邻域内。
死区是一种很常见的非线性环节,比如对于直流电机、伺服阀等,死区的存在会降低控制精度,限制控制性能,对控制设计增加难度。逆模型补偿[14]通过直接加入死区的逆模型,从而抵消死区的影响。文献[15]将线性死区扩展到了非对称的死区,并设计一种自适应补偿算法,实现对期望轨迹的精确跟踪。文献[16]针对一类具有非对称致动器死区的多输入多输出系统,提出了一种新型的近似模型,并设计鲁棒自适应律,实现误差渐近收敛。文献[17]针对带有死区输入非严格反馈系统,提出一种有限时间在线最优跟踪控制算法,实现跟踪误差的有限时间收敛。但是,当系统为有限区间非参数不确定系统时,单一自适应难以实现高精度的跟踪控制。因此,本文采用迭代学习控制,通过迭代学习进一步提高精度。
基于上述讨论,本文针对具有非对称死区输入的非参数不确定系统,提出一种误差跟踪迭代学习控制算法,在指定区间内实现对期望轨迹的高精度跟踪。利用中值定理将非对称死区转换为线性形式,并利用径向基函数(radial basis function,RBF)神经网络对系统的不确定性进行逼近。针对ILC 初值问题,设计新型期望误差轨迹,使得系统迭代初始值可任意设置,放宽经典ILC 的初值一致条件。此外,本文基于Lyapunov-Like 理论,构造迭代学习控制器和组合自适应律,实现跟踪误差沿预设的期望误差轨迹收敛到0 的邻域附近。
1 问题的提出和预备知识
1.1 问题的提出
考虑一类具有非对称死区输入的非参数不确定系统,其表达式为

其中,k(k=0,1,2,…) 表示迭代次数,t∈[0,T]表示运行时间,T为迭代长度,xk=[x1,k,x2,k]T∈R2表示系统状态,f(x) 为未知光滑但有界的非线性函数,f(x) 反映了系统中的非参数不确定性,b表示未知的常数控制增益且满足b >0,yk∈R表示系统输出,vk=vk(t) ∈R表示系统控制输入,D(vk) 表示非对称死区环节,其模型具体为
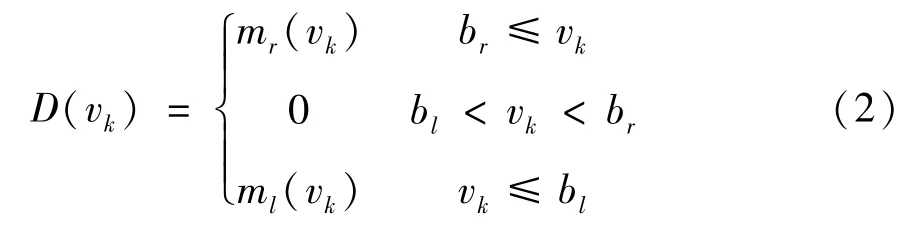
其中,mr(vk)和ml(vk) 表示未知且光滑的非线性函数,br >0和bl <0 为常数,表示未知的死区宽度。如图1 所示。

图1 非对称死区
本文控制目标是针对具有非对称死区输入的非参数系统式(1),设计误差跟踪迭代学习控制器vk,使得当迭代次数k趋向无穷时,在任意初态下,实现系统输出x1,k对期望轨迹xd的高精度跟踪。
1.2 预备知识
RBF 神经网络对未知的光滑非线性函数有良好的逼近作用,因此RBF 神经网络经常被用于估计光滑的非线性函数。对于任意光滑的未知函数h(x),存在一个神经网络使得

其中,X∈ΩZ为输入向量,ΩZ∈R为一紧凑子集;ε为逼近误差,存在一个正常数εN,满足| ε|≤εN;ϕ(X)=[ϕ1(X),…,ϕl(X)]T∈Rl为神经网络的基函数,l(l >1) 为神经网络的节点数;W∗∈Rl为理想权重矩阵,定义为

其中,W∈Rl为权重矩阵,选择高斯函数

其中,wi为中心点,ηi表示宽度。
2 误差跟踪迭代学习控制
2.1 误差定义与系统转换
定义跟踪误差如式(6)所示。

其中,xd表示期望输出轨迹,表示期望轨迹的一阶导数。
根据跟踪误差的定义,将系统式(1)转换为误差形式:

其中表示期望轨迹的二阶导数。
在进行控制器设计和稳定性分析之前,需要对死区环节进行如下假设。
假设1函数ml(vk)和mr(vk) 光滑且存在未知的正常数ml0、ml1、mr0和mr1,使得

考虑到ml(bl)=mr(br)=0,根据微分中值定理,非对称死区环节式(2)可以重写为
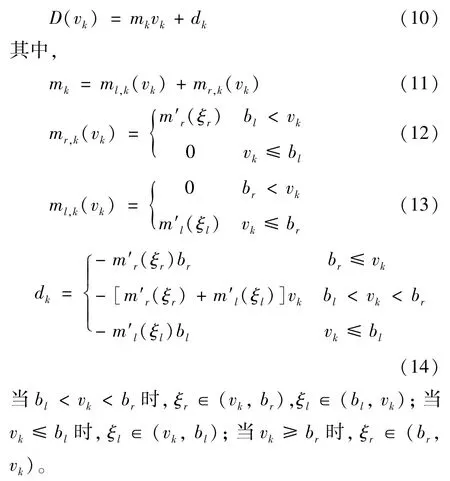
根据假设1 和式(10)~(14),可以证明时变参数mk和dk的有界性。

由此,可以将式(7)进一步写成

注1当-bl=br,ml(vk)和mr(vk) 为常数时,非对称死区环节式(2)表示为传统的对称线性死区。因此,非对称死区更具有代表性,对非对称死区进行研究具有理论意义。
2.2 期望误差轨迹设计
传统的迭代学习控制器设计需要系统满足初值一致条件[6-7],具体为

式(18)需要在每次迭代中都要恒成立,即对∀k成立。但是,系统在实际运行过程中,由于建模的不确定性、外部干扰、机械精度等原因,导致条件式(18)不能在任意次迭代中恒成立。
因此,本文设计了一种新型的期望误差轨迹,有效避免了条件式(18)的限制,表达式如式(19)所示。

期望误差轨迹式(19)满足下列等式性质:
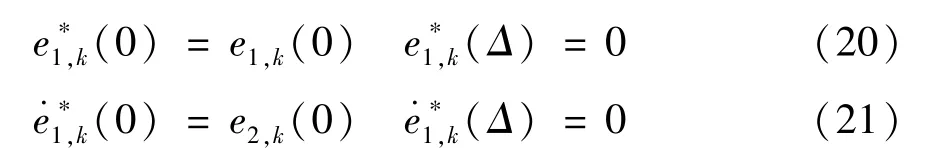
式(19)的构造只需要知道系统的误差初值e1,k(0) 及其导数的初值e2,k两个信息,此外,接入点(t=Δ)的导数设置为0,简化了期望误差轨迹接入点时刻的导数信息。由于期望误差轨迹的设置与期望轨迹xd无关,因此对于不同的期望轨迹,期望误差轨迹的形式无需改变。
图2 反映了期望误差轨迹的变化情况。当误差轨迹跟踪上期望误差轨迹时,由于期望误差轨迹在[Δ,T] 为0 误差轨迹,因此状态轨迹能在指定区间[Δ,T] 实现对期望轨迹的高精度跟踪。对比式(18)和式(19),可以发现传统迭代学习控制中是对系统状态初值进行限制,而本文所提方法是通过限制期望误差轨迹来避免限制系统状态初值。期望误差轨迹可以随迭代变化,而系统状态初值的精确重置由于环境因素难以保证。
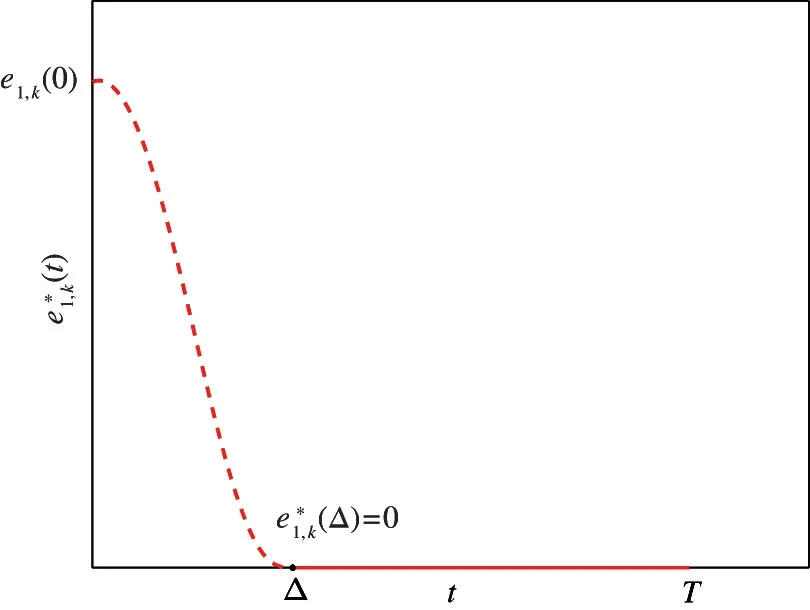
图2 期望误差轨迹
2.3 误差跟踪迭代学习控制设计

对式(26)求导,得到:

3 收敛性分析
定理1针对系统式(1),给定期望轨迹xd,设计期望误差轨迹式(19),虚拟控制器式(24),实际控制器式(30),组合自适应律式(31),跟踪误差在任意初态下沿着预设轨迹收敛以L2范数的形式收敛到0 点附近的邻域内。
证明定义复合能量函数:

对式(33)进行求导,由第2 节的分析,可得:


证毕。
4 仿真结果及分析
考虑如下系统[18]:

本节以一个具有死区输入非参数不确定系统式(44)进行验证所提误差跟踪迭代学习控制方法的有效性,并将本文所提方法(M1)与自适应控制方法(M2)进行对比。
M1 为本文提出的误差跟踪迭代学习控制方法,包括期望误差轨迹式(19)、虚拟控制器式(24)、实际控制器式(30)和组合自适应律式(31)。
M2 为自适应控制方法,其虚拟控制器和实际控制器分别设计为
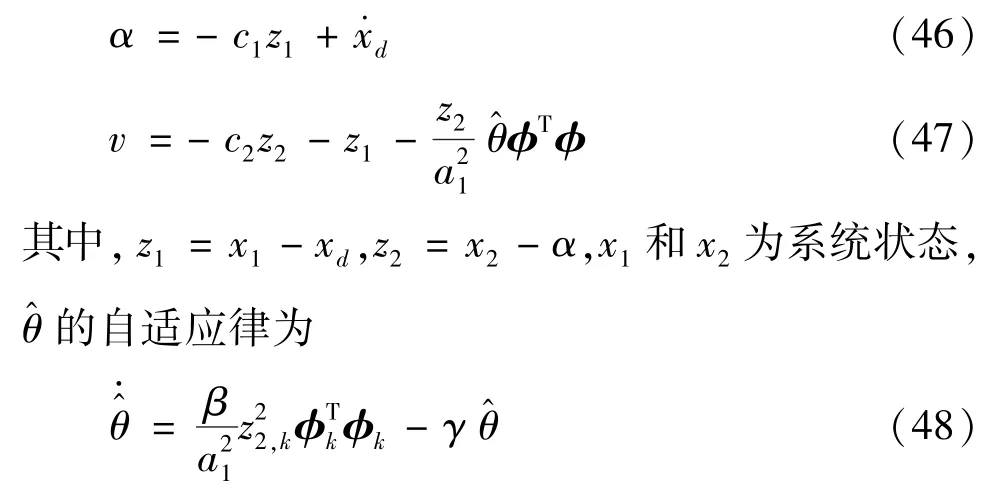
γ为满足γ >0 的常数。
系统期望轨迹设定为xd(t)=0.2cos(πt),系统的迭代长度设定为T=5 s,采样时间为tc=0.001 s。控制器和学习律参数如表1 所示。
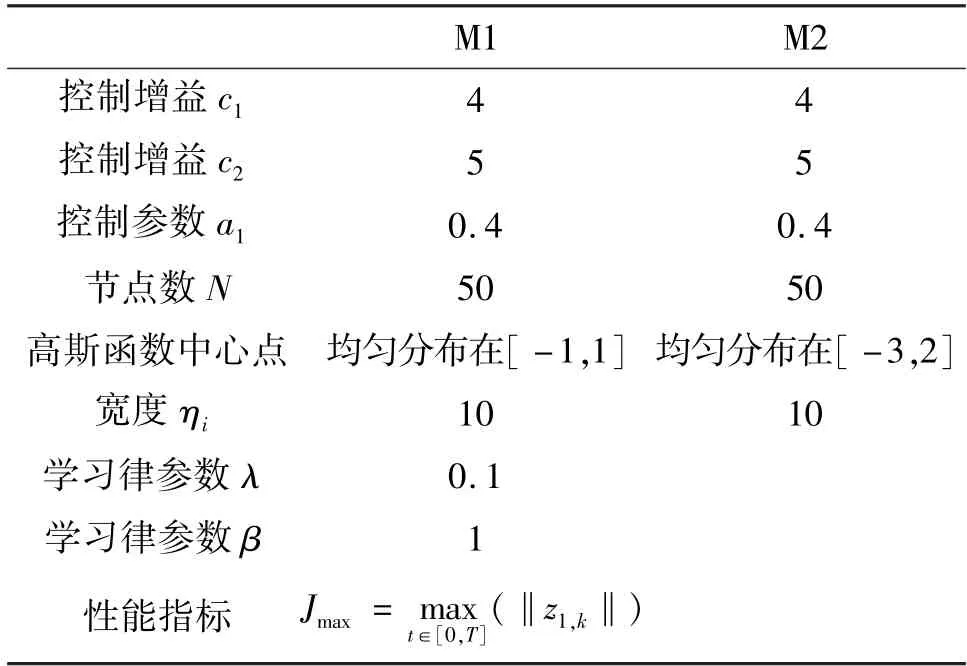
表1 参数表
仿真结果如图3~图7 所示。图3 为M1 和M2 方法的状态跟踪效果图。可以发现,当迭代次数为50时,本文所提M1 方法比M2 方法具有更高的跟踪精度。图4 为M1 和M2 方法的误差跟踪效果图,可以发现M1 方法的误差能沿着预设的期望误差轨迹收敛,并且稳态误差比M2方法更小。图5为k=1、10、50 时的误差跟踪图,从图中可以看出,对于任意初值,误差初值都能与期望误差初值重合,从而避免了初值一致条件,与上述理论一致。图6 给出了M1和M2 的控制信号与死区输入,可以发现,M1 和M2的实际输入信号相差不明显。图7 反映了性能指标Jmax的变化情况,由图可知,随着迭代次数的不断变化,本文所提方法M1 的最大误差逐渐减小,控制精度不断提高。综合图3~图7,可以得到以下结论,针对具有死区输入的非参数不确定系统,本文所提方法M1 能实现在任意误差下,误差沿着期望误差轨迹收敛,并且在指定区间[Δ,T] 上实现对状态的高精度跟踪。

图3 状态跟踪效果(k=50)

图4 误差跟踪效果图(k=50)

图5 在不同迭代次数中M1 的误差跟踪效果

图6 控制信号和死区输出
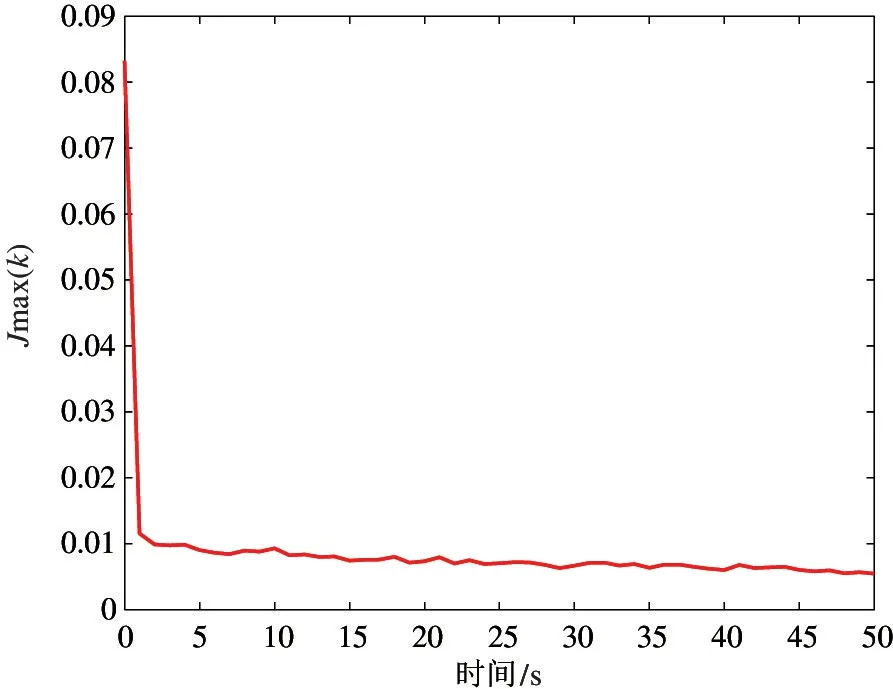
图7 性能指标
5 结论
本文针对一类具有死区输入的非参数不确定系统构造了一种误差跟踪迭代学习控制方法。通过设计新型期望误差轨迹,放宽了传统ILC 的初值一致条件,同时预设了误差的收敛轨迹。利用RBF 神经网络对系统中的不确定性和死区参数进行估计,并设迭代学习控制器和组合自适应律,使得误差在指定区间内收敛到0 附近一个很小的邻域内。最后,基于Lyapunov-Like 理论进行稳定性分析,并通过仿真验证该方法的有效性。
