量子力学的数学基础

杨师杰

(北京师范大学 物理学系，北京 100875)

大学教授量子力学通常从引入薛定谔方程开始，以求解不同条件下的薛定谔方程本征值问题贯穿始终，但是对于为何存在本征值问题，本征函数的完备性则略而不谈，相关的数学物理方法课程也只述结论，不表原因，这致使量子力学的数学基础一直不甚了了.本文试图从线性空间的内积开始，对量子力学的数学基础做一个系统的描述[1]，以期对教学产生有益的辅助作用.

1 线性空间基础

1.1 度量空间

范数用来表征某个线性向量空间中向量的长度，记做‖x‖，满足条件‖x‖≥0，定义了范数的向量空间称为赋范空间.设是一个非空集合，对其中任意两点x、y，引入一个相应的实数d(x，y)，满足：1) 正定性：d(x，y)≥0，当且仅当x=y时，d(x，y)=0；2) 对称性:d(x，y)=d(y，x)；3) 三角不等式:d(x，y)≤d(x，z)+d(z，y).则称d(x，y)为中的一个度量，称为定义度量d(x，y)的度量空间.

度量空间是将欧几里得空间的距离概念做推广的一个抽象数学结构，它采用集合中两个元素之间的度量取代欧几里得空间中两点之间的距离，可以包括向量距离、函数距离、曲面距离等.赋范空间和度量空间的区别，在于度量定义于任意非空集合，而范数仅定义于向量空间.

当空间定义了度量之后，就可以比较空间中两点之间的距离，度量空间的柯西序列可表述为:设(，d)为度量空间中的点序列x1，x2，…，xk，…∈，如果对于任意正实数ε>0，存在正整数N(ε)，当n，m>N(ε)时，度量(距离)d(xn，xm)<ε，则该序列称作柯西序列，用极限表示，即

任何紧致集合都是完备的，但反过来不成立.比如实数集虽然是完备的，但不是紧致的;只有加上∞后，才构成紧致闭集合，它等价于一个圆周.有限维的欧几里得空间在通常的距离定义下是完备的，而无限维空间的完备性，则是下面需要专门探讨的课题.

1.2 内积空间

一般的线性向量空间定义中并不包含向量与向量之间的乘法，为此引入内积概念，用符号〈a|≡(|a〉)†表示向量|a〉的对偶向量，有

(α|a〉+β|b〉)†=α*〈a|+β*〈b|

其中星号表示取复共轭.狄拉克将向量|a〉称为右矢，向量〈a|称为左矢，分别表示括号的一半[3].

设有n维线性向量空间，向量|a〉，|b〉，|c〉∈，在复数域上定义内积〈a|b〉∈，满足如下条件：

1) 〈a|b〉=〈b|a〉*;

2) 〈αa+βb|c〉=α*〈a|c〉+β*〈b|c〉;

3) 〈a|a〉≥0，当且仅当|a〉=0时，〈a|a〉=0.

内积将一对向量与一个实数或复数标量联系起来，用符号表示为×.如果两个非零的向量满足〈a|b〉=0，则称它们互相正交.定义了内积的线性向量空间称作内积空间，当内积为实数时称作欧几里得空间，内积为复数时称作酉空间.

内积的定义区别了内积空间与一般向量空间，它包含3个运算:向量与向量之间的加法，标量与向量之间的乘法，以及向量与向量之间的乘法.内积实际上也定义了一个度量，因此内积空间也是度量空间.

1.4 自伴算符

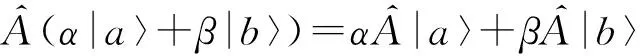
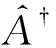
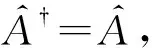
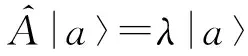
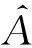
2 希尔伯特空间

有限维线性向量空间的基本思想，其中的概念如线性叠加、线性无关、内积、子空间等，都可以直接推广到无限维空间.然而有一件事至关重要，那就是向量无穷求和的收敛性，或者说无穷维向量空间的完备性，这个并非平庸的问题赋予无限维空间更加深刻的性质[1].

2.1 贝塞尔不等式

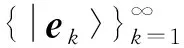
所以有贝塞尔不等式：

则称该空间是完备的.

2.2 完备性关系

内积空间如果是完备的，则称作希尔伯特空间，记做H，所有完备的有限或无限维内积空间都是希尔伯特空间.完备性表明帕塞瓦恒等式成立，即

所以有

该式也被称作基向量的完备性关系.

2.3 函数空间

定义在区间[a，b]的连续函数可视作一个向量，该区间内所有连续函数构成一个线性向量空间，但这个空间并不是完备的.如何构造一个完备的内积空间呢?首先，需要定义两个函数向量的内积，它很自然地与函数的积分相联系.一般地，将函数空间的内积定义为

其中ρ(x)是一个正定的实函数，称作权重函数，以后会讨论到.本文有时为了方便，简单地取ρ(x)=1.令f(x)=g(x)，则其范数为

因此内积空间要求所有函数必须是模方(加权)可积的.

前面称完备的无穷维内积空间是希尔伯特空间.本定理表明，希尔伯特空间的数量是很有限的，它等同于我们熟悉的平方可积函数空间.一般来说，平方可积性并不要求函数是连续的.它只要求函数分段光滑即可.

2.4 连续基

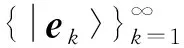
无限不可数空间向量|f〉在基{|ex〉}x∈表示下的分量f(x)，则被视作连续实数集合的函数：

向量分量f(x)即为函数向量|f〉在连续基表示下的函数.

该式意味着

物理学家习惯忽略掉e，而将基向量写作|x〉，则连续指标的完备性关系为

将向量|f〉用|x〉表示为

其中x′∈(a，b)，可见ρ(x)〈x′|x〉=δ(x-x′)，即狄拉克δ函数.如果取权重ρ(x)=1，得到连续基的正交完备关系：

在量子力学中，如果连续基是位置则称作坐标表象;如果连续基是动量则称作动量表象.希尔伯特空间的态向量在连续基下的表示称作波函数，在不同连续基之间的转换称作表象变换[4].

3 施图姆-刘维尔系统

3.1 伴随算符

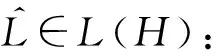
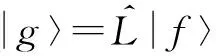
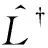
(p2vu′+p1vu)′-(p2v)′u′-(p1v)′u+p0uv=

[p2vu′-(p2v)′u+p1vu]′+

u[(p2v)″-(p1v)′+p0v]=

其中算符：

对区间[a，b]进行积分，可得

该式称为拉格朗日恒等式，它可以视作另一种形式的格林公式.

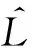
则有

一个算符的伴随算符与该算符的形式有关，伴随算符的边界条件也与原算符的边界条件不同.

3.2 自伴算符

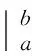
定义在区间x∈[a，b]的形如

的二阶常微分方程，被称作施图姆-刘维尔本征方程.由于ρ(x)〉0，令

方程可化为标准的本征方程：

则

由拉格朗日恒等式得

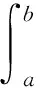
注意到施图姆-刘维尔算符成为自伴算符的前提是上式右边为零，即

因此对于不同本征值λ1≠λ2，其对应的本征函数是(加权)正交的：

可以有3种不同方式满足上述边界条件[4]:

1) 如果端点满足第一类齐次边界条件(狄里希利边界条件)，或第二类齐次边界条件(纽曼边界条件)，这显然是可以实现的.

2) 如果端点满足第三类齐次边界条件(混合边界条件)，比如在x=a端满足

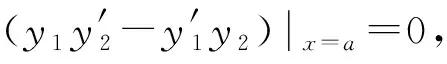
3) 虽然不满足齐次边界条件，但是如果在端点p(x)为零，比如p(a)=0，同样可以达到此目的，这就是所谓自然边界条件.由于具有有限解的微分方程通常只能含有正规奇点，容易证明p(x)在端点必为一阶零点，自然边界条件也称为奇异边界条件.

传统的量子力学理论要求力学量算符必须是自伴算符，这样当它作用于态向量后，本征值都是实验可观测的实数，且本征向量是正交的.许多量子力学问题没有齐次边界条件，比如谐振子定态方程，氢原子电子运动方程，或者磁场中电子的运动方程等，而且有时候方程在无穷远点出现非正规奇点，这时需要仔细鉴别出自然边界条件，以确保量子系统构成施图姆-刘维尔本征值问题.本文最后一节给出几个示例来展示这一过程.

3.3 基本性质

由于施图姆-刘维尔型方程的本征函数具有带权重的正交性以及完备性，如果函数f(x)具有连续的一阶导数和分段连续的二阶导数，且满足本征函数族所满足的边界条件，就可以用这些本征函数y1(x)，y2(x)，y3(x)，…的线性叠加表示，称作广义傅里叶级数展开：

本征函数族称作级数展开的基，展开系数为

近年来凝聚态物理前沿领域中出现许多讨论非自伴或非厄米哈密顿量的研究.在这种情况下，本征能量为复数，本征函数也不再是正交的，而周期结构的能带将呈现出特殊拓扑性，以及皮肤量子态等特征，这是一个量子理论发展的新动向.值得指出的是，非厄米系统希尔伯特空间的完备性问题仍然未被完全理解.

4 量子力学示例

我们取自然单位ћ=m=1，讨论两个薛定谔定态方程的具体应用作为示例.

1) 一维谐振子运动方程：

该式化为标准的施图姆-刘维尔型为

得到p(ξ)=e-ξ2，由此可知u(ξ)在无穷远点存在自然边界条件，因此该方程的无穷级数解可以截断为厄米多项式，由此确定本征值λ=n(n∈)以及相应的本征函数.

2) 氢原子的电子运动方程

在球坐标系中分离变量ψ(r，θ，φ)=R(r)Ylm(θ，φ)，其中角向部分即为球谐函数Ylm(θ，φ)，对应的本征值为l(l+1)，径向部分满足方程：

可见r=0是方程的正规奇点，但r=∞是方程的非正规奇点，暂时不能确定在无穷远点是否存在自然边界条件.

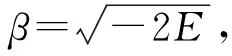
ry″+[2(l+1)-2βr]y′-2[(l+1)β-1]y=0

再令

有

ξy″+(γ-ξ)y′-αy=0

其施图姆-刘维尔本征方程为

其中p(ξ)=ξγe-ξ，这样就证明函数y(ξ)在ξ=0，∞均存在自然边界条件，方程的无穷级数解为库默尔函数：

虽然该级数的收敛半径为无穷大，但在ξ=∞级数仍然发散，为此将无穷级数截断为多项式，即将α参数取为负整数：

α=-nr， (nr=0，1，2，…)

最后总结一下，如果r=∞是方程的非正规奇点，通常没有自然边界条件，方程的解不宜直接表示为弗罗贝尼乌斯级数形式.函数变换R(r)y(r)改变了r=∞的奇异性，使得函数y满足自然边界条件，发散级数可截断为多项式.在量子力学中，我们习惯上认为r→∞时波函数ψ(r)→0是薛定谔方程之外附加的物理要求，其实这是方程本身存在自然边界条件的结果，正所谓方程决定物理.

作为反例，贝塞尔方程在x=∞为非正规奇点，其级数解的收敛半径为无穷大，完全不必做截断处理.但由于在x=∞缺少自然边界条件，方程不能构成完备的本征值问题.必须在有限半径的圆周上附加以齐次边界条件，与x=0的自然边界相结合，才能构成完备的本征值问题.