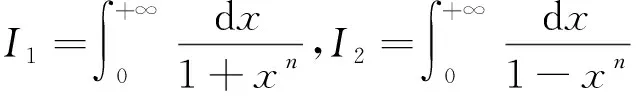再谈由留数定理求解的两类无穷积分

周运清，黄文涛

(浙江海洋大学 信息工程学院物理系，浙江 舟山 316022 )

最近，周文平、刘奕帆和宋铁磊3位同行发表了题为《由留数定理求解的两类无穷积分》的文章，该文讨论了两类通过留数定理可以求解的无穷积分，一类是实轴上无奇点的情况，另一类是实轴上有奇点的情况[1,2]，这两类积分很有代表性，且推导过程详细，思路清晰，适合在教学过程中采用，非常有教学意义. 基于上述原因, 我们想进一步谈谈这两类积分，主要从两方面来讨论，一是对两类积分的积分过程进行简化和必要说明，厘清问题的本质，便于以后碰到类似问题能灵活处理；二是通过多值函数的方法[3]，把两类积分的适用范围进行拓展，即n由大于1的整数拓展为大于1的实数，最后可让学生在课堂上把2种方法得到的结果进行比较，看是否能相互印证，这样对两类积分的理解会更全面和深刻.

1 积分类型(n为实数且n>1)

1.1 积分的简化处理与说明

对于这类积分，积分范围内无奇点，可以证明该积分对于n>1收敛，即

(1)

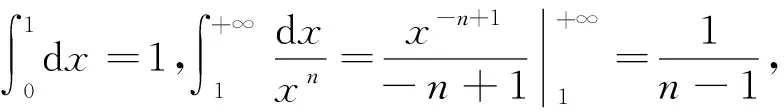
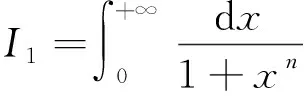
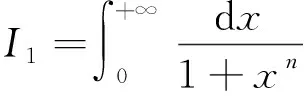
(2)

图1 积分回路

而回路积分由2段直线段和圆弧构成，因而又可以写为3部分积分之和，即

(3)

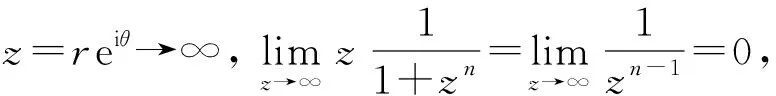
(4)

由式(4)可推得

(5)

值得注意的是，在上述推导过程中，n≥2，且为整数，对于n为非整数不适用.本小节在利用留数定理的推导过程中，仅要求n为大于1的整数，且说明了为什么要取图1这样的积分路径, 其他路径可让学生自己去练习，并对比了几种路径计算所需的工作量.

1.2 多值函数留数定理方法求实积分I1

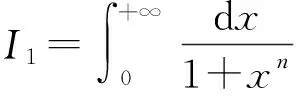
(6)

而回路由几部分构成，可写成如下各部分积分之和：

(7)

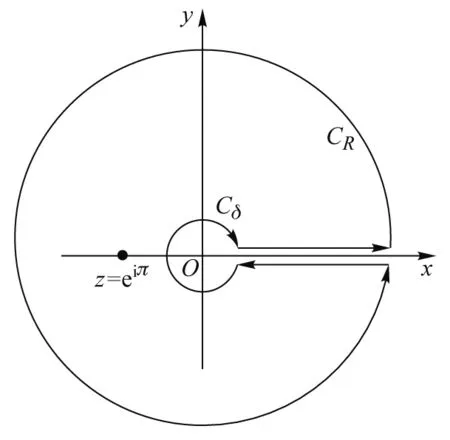
图2 积分回路

由于

因而由小圆弧引理和大圆弧引理可得

因而由式(7)可得

(8)

由式(6)与式(8)可推得

(9)

从而得到积分I1的结果：

(10)

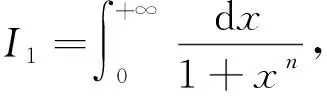
2 积分类型(n为实数且n>1)

2.1 积分的简化处理与说明

(11)

图3 积分回路

而回路积分由4段直线段，两个半圆周和一个大圆弧构成，因而又可以写为7部分积分之和，即

(12)

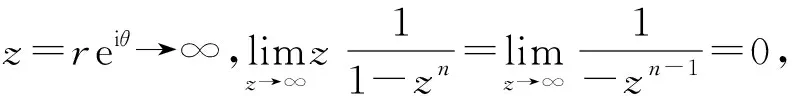
当δ→0时，则在C0δ上有

(13)

由小圆弧引理可得

同理在C1δ上有

(14)

所以当r→+∞，δ→0时，由式(11)—式(14)得

(15)

从而有

(16)

式(16)中要求n>1的整数，本节和1.1节的差异在于积分路线上存在奇点，处理方法为以奇点为圆心且半径无限小的半圆绕过奇点，半圆的积分值可由小圆弧引理或留数定理来计算.

2.2 多值函数留数定理方法求实积分I2

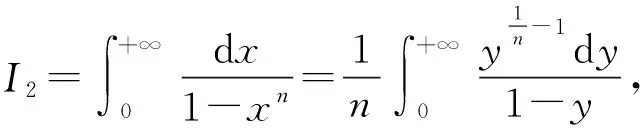
f′2(z)dz=0

(17)

而

(18)

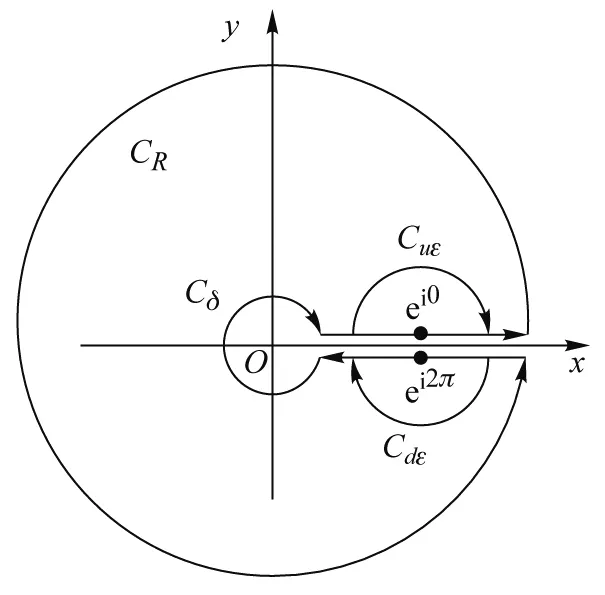
图4 积分回路

由于

(20)

因而由小圆弧引理和大圆弧引理可得

(21)

(22)

由式(17)、式(18)、式(21)、式(22)可得

(23)

最终求得

(24)

本节思路与1.2节类似，只是在积分路线上有奇点，处理方法与2.1节方法相同.值得注意的是，割线上岸任一点的辐角规定为2kπ，则按积分回路的绕向，下岸任一点的辐角为2(k+1)π，这样也可求得I2，这种情况可留作学生自行练习，对多值函数的理解会有好处.

3 小结