5G网络中无人机-车辆非平稳信道模型与统计特性分析*

张晓华，彭 小，黄 龙

(重庆市信息通信咨询设计院有限公司，重庆 400065)

0 引 言

5G通信技术的出现，推动了无人机(Unmanned Aerial Vehicle,UAV)与车辆通信朝着数字化、智能化方向飞速发展，设备像物联网一样随时随地相互通信，收发端不再是固定在某个位置，而是有规则或无规则运动[1-2]。

自4G通信以来，主流信道模型研究基本都是基于三维建模的，在5G逐渐登上通信舞台的同时，基于几何随机的三维无人机与车辆的信道模型研究是必不可少的。在文献[3-8]的几何随机模型研究中，并没有综合地考虑一次散射、二次散射以及地面反射径等其他路径的叠加影响，并且某些模型忽视了根据信道环境合理设置散射体运动或静止状态，导致研究非平稳特性时缺少散射体运动状态的影响。

针对以往模型中收发端运动时速度大小和速度方向较为固定的不足，文献[9]提出了一种发送端允许加速和曲线运动的三维非平稳几何随机信道模型，并研究了相关统计特性；文献[10]采用了高斯-马尔科夫迁移率模型来模拟收发端速度和轨迹；文献[11]提出了一种散射体以任意速度任意方向运动的非平稳几何随机信道模型，并通过马尔科夫生灭过程演进散射体簇的变化；文献[12]提出了基于无人机场景的任意轨迹无人机的非平稳几何随机信道，并研究了不同速度方向角对无人机信道的影响。

综上所述，以往无人机到车辆(Unmanned Aerial Vehicle to Vehicle,UAV-V)通信场景的非平稳信道研究中，在信道建模方法上仍存在一些不足。因此，本文主要针对无人机到车辆非平稳信道建模展开进一步研究，主要贡献如下：

(1)提出了一种基于椭圆-圆柱-半球几何随机非平稳UAV-V信道模型——对于一次散射径的散射体分布，使用同心椭圆面几何随机模型模拟；对于二次散射径的散射体分布，使用了同心圆柱-同心半球体几何随机模型模拟，并且还使用了半球底面同心圆模型对地面一次反射分布进行了模拟;

(2)基于所建立的模型，推导了空时相关函数(Space-Time Correlation Function,STCF)和多普勒功率谱密度(Doppler Spectral Density，DPSD);

(3)基于上述统计特性的表达式，对无人机到车辆信道统计特性以及信道非平稳性进行了仿真分析。

1 UAV-V非平稳信道建模与统计特性

1.1 信道几何模型描述

本文采用5G频段，假设对城市场景中UAV-V通信系统建立信道模型。这里使用同心圆柱体来模拟无人机周围散射体分布，使用同心半球体模拟车辆周围散射体分布。该信道模型由视距与非视距分量组成，其中非视距分量由一次散射、二次散射和地面一次反射分量组成，通信系统如图1所示。

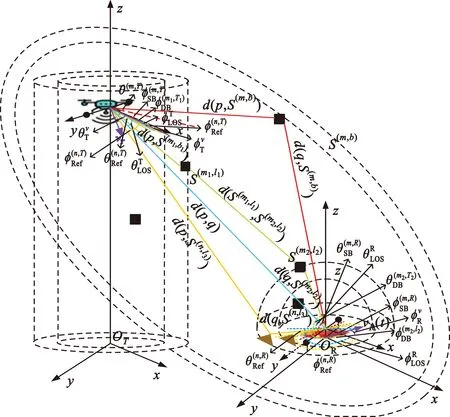
图1 UAV-V通信系统

图2为图1中一次散射分量椭圆几何分布在x-y平面的投影，投影图中显示了收发端速度方向、位置变化以及角度变化。

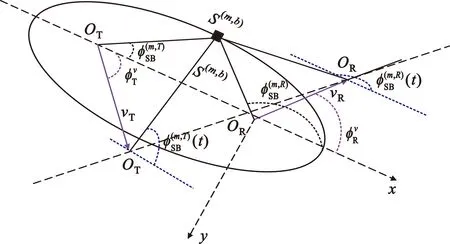
图2 UAV-V一次散射x-y平面投影

图3为图1中二次散射径的圆柱-半球几何分布在x-y平面的投影，投影图中显示了收发端方向变化、角度变量的几何关系和速度方向变化。

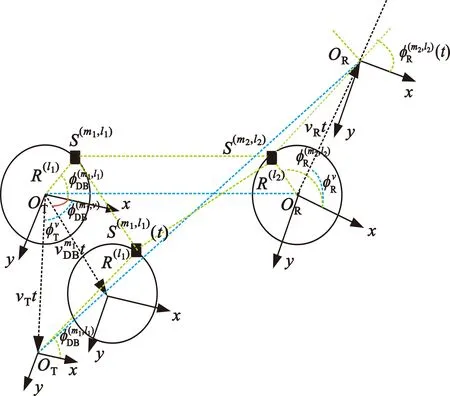
图3 UAV-V二次散射径x-y平面投影

1.2 信道参数描述

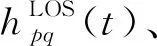
(1)

1.2.1 视距参数

(2)

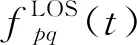
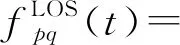
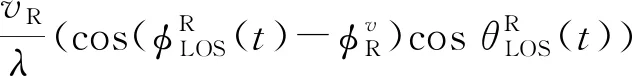
(3)

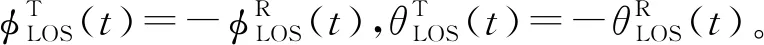
(4)

(5)

1.2.2 一次散射分量参数

本节进一步展开公式(1)中的一次散射分量冲激响应，可表示为

(6)

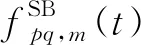
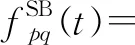
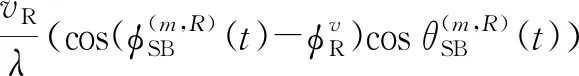
(7)

(8)

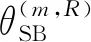
(9)

(10)

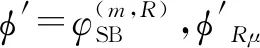
(11)

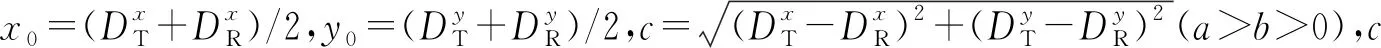
(12)

(13)

(14)

(15)

(16)

(17)

又由几何关系可得

(18)

(19)

结合公式(16)～(19)可得

d(p,S(m,b))(t)=

(20)

d(q,S(m,b))(t)=

(21)

1.2.3 二次散射分量参数

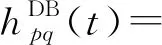
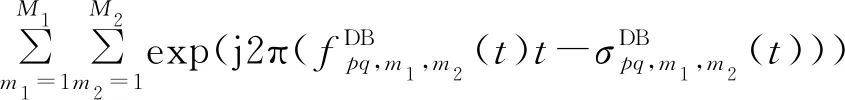
(22)

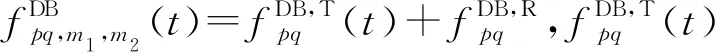
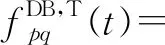
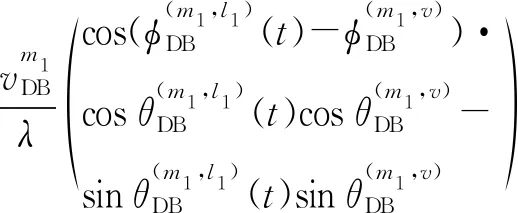
(24)

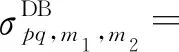
d(q,S(m2,l2))(t))/λ。

(25)

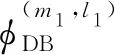
(26)

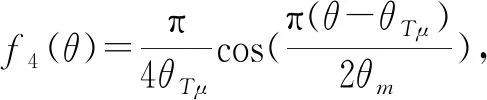
(27)

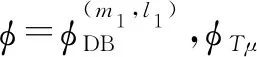
(28)

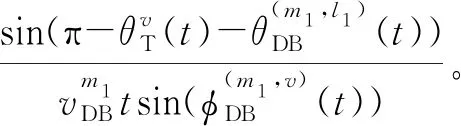
(29)

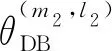
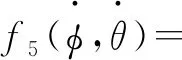
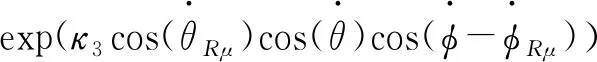
(30)

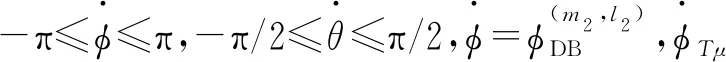
(31)

(32)

(33)

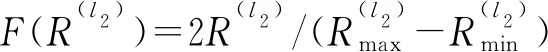
同理，由几何关系可得，l1同心圆柱面上的第m1个一次散射体位置矢量dS(m1,l1)(t)表示为

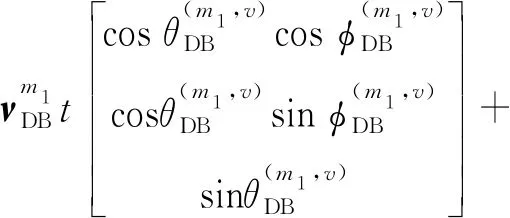
(34)

l2同心圆柱面上的第m2个一次散射体位置矢量dS(m2,l2)描述为

(35)

因此，由式(34)和式(35)可进一步得出

(36)

(37)

(38)

d(S(m1,l1),S(m2,l2))≈d(p,q)(t)-

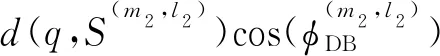
(39)

由式(25)与式(39)进一步可得出

(40)

(41)

(42)

1.2.4 地面一次反射分量参数

(43)

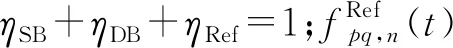
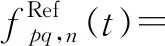
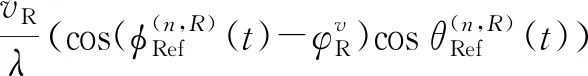
(44)

(45)

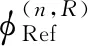
(46)

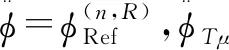
1.3 UAV-V非平稳信道统计特性

1.3.1 空时相关函数

公式(1)中hpq(t)的信道空时相关函数可表示为

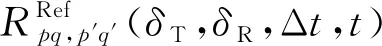
(47)

(48)

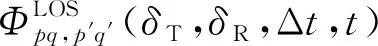
(49)

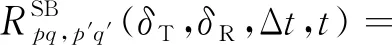
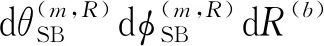
(50)

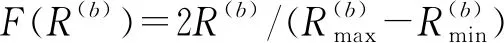
(51)

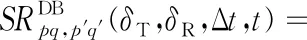
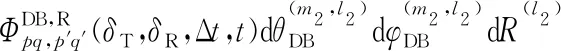
(52)

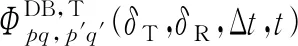
(53)

(54)

(55)

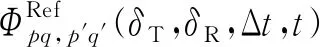
(56)

1.3.2 多普勒功率谱密度函数

多普勒功率谱密度S(f,t)可由时间ACF的傅里叶变换推得。令δT=0，δR=0，式(47)中Rpq,p′q′(δT,δR,Δt,t)变为Rpq(Δt,t)。因此，DPSD表示为

(57)

2 仿真分析

系统仿真参数设置如表1所示。

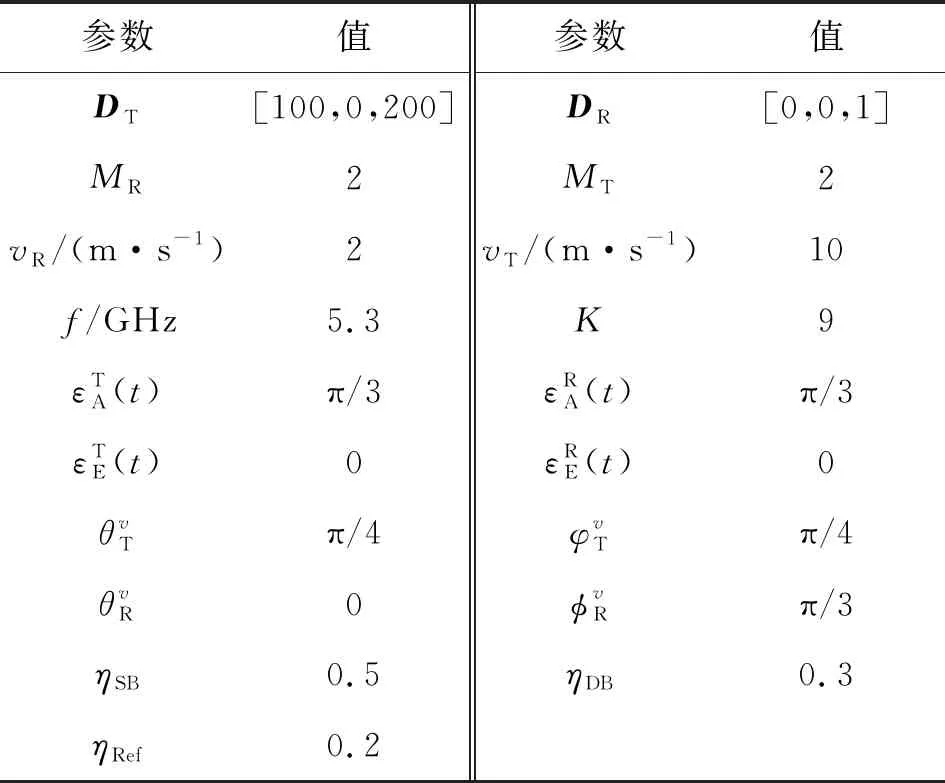
表1 系统仿真参数表

为了描述各径分量的信道统计特性，本文各分量相关参数设置如表2所示。

表2 各径分量参数设置

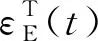
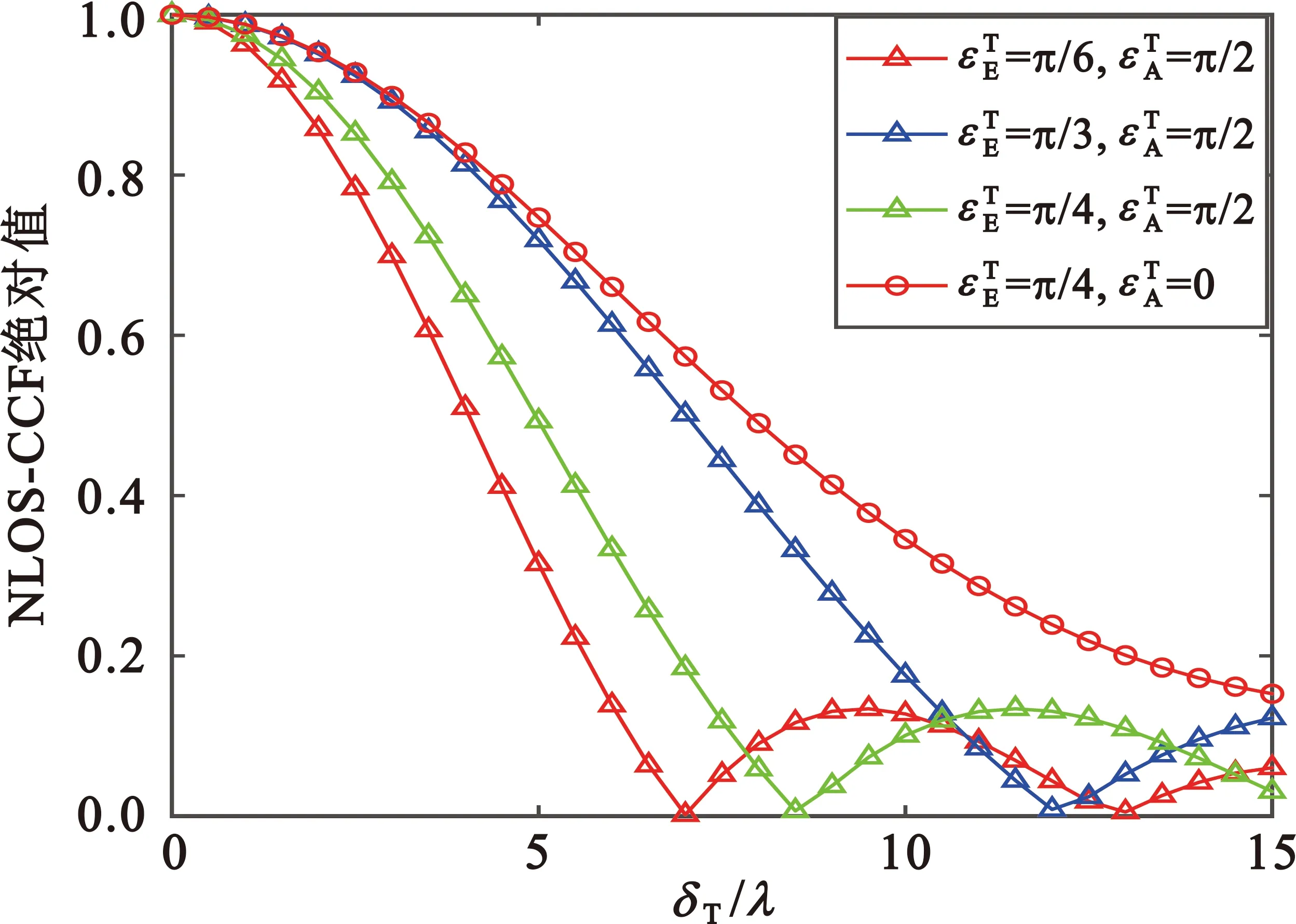
图4 不同天线仰角方位角非视距空间CCF绝对值

为了进一步分析非视距分量空间CCF与收发端距离关系，本节将无人机位置分别设置为[100,0,200]，[200,0,300]，[200,500,300]，图4给出了不同无人机位置下的空间CCF变化曲线，可以看出，收发端距离越大，视野越广阔，非视距更接近视距情况，因此空间相关性越高。

图5 不同无人机位置非视距空间CCF绝对值

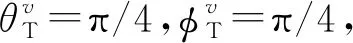
图6 无人机在不同方向移动的DPSD变化

图7给出了各模型的时间ACF值随着Δt变化曲线，其中包括本文非视距分量以及本文非视距下各分量、文献[2]无人机非视距测量值和文献[4，6]无人机到地模型。通过将本文模型与无人机测量模型的时间ACF进行对比，结果表明，理论模型与真实测量模型ACF变化较为接近。同时，本文模型与文献[6]模型对比发现，本文模型的变化趋势与其较为相似，并且波动趋势类似于一次散射径的时间ACF波动趋势。这是由于本文模型增加二次散射径分量所致，同时一次散射径分量所占比例要大于二次散射径分量。本文模型与文献[6]对比发现，本文模型的时间相关性明显高于文献[6]模型，且波动较为平缓。这是由于本文采用同心圆柱和半球体来模拟UAV-V信道环境中散射体分布，而文献[6]仅考虑半球体模拟接收侧散射体分布。综上所示，鉴于本文模型在各模型中的优越性，可以将其作为无人机与车辆非平稳信道模型建模方案的参考。

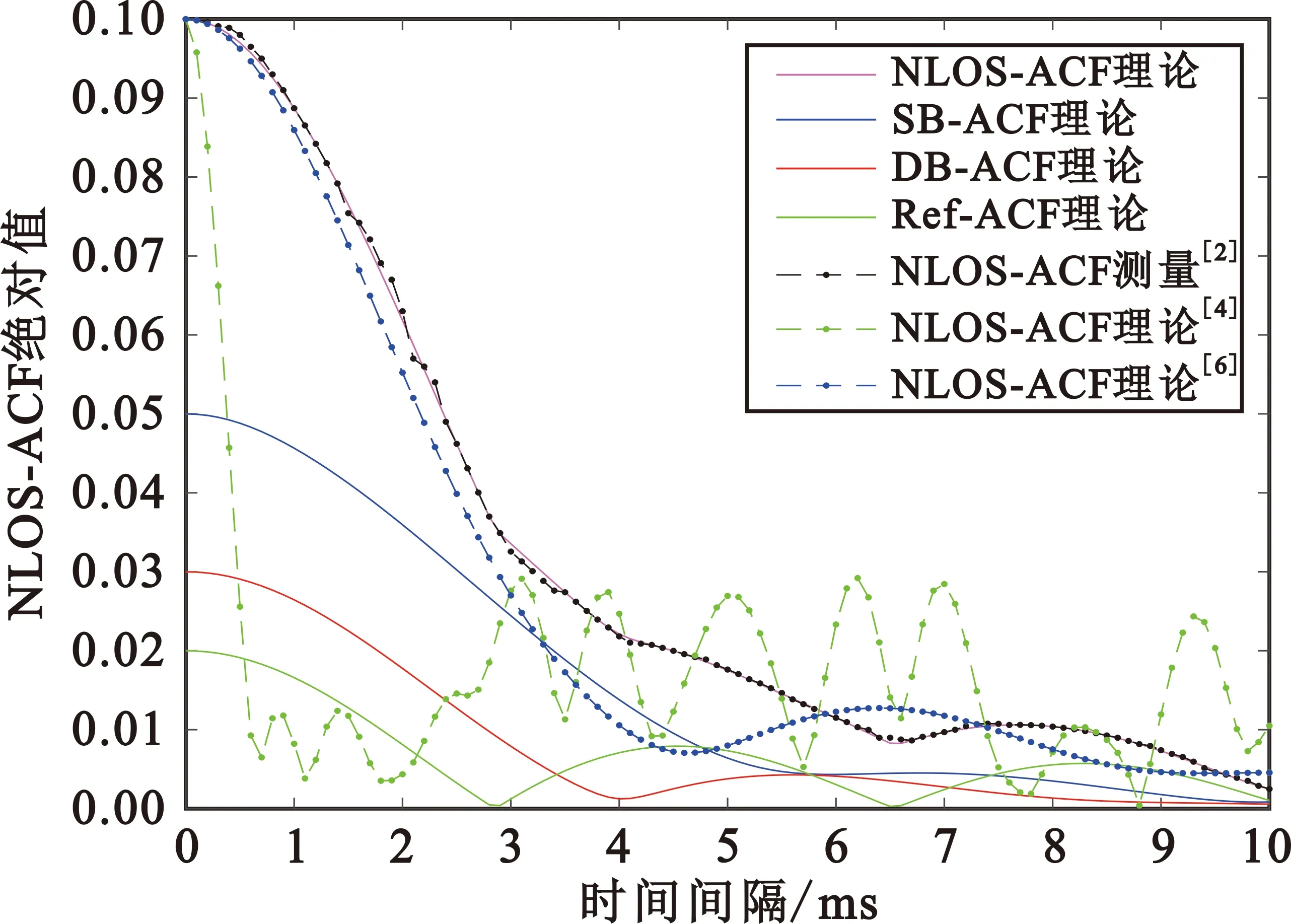
图7 不同模型的非视距时间ACF变化

3 结束语

本文基于UAV-V信道场景提出了一种新型UAV-V非平稳信道模型。该模型考虑了无人机侧和车辆侧散射体不同分布状态，使用椭圆面模拟一次散射中散射体分布，同心圆柱体来模拟无人机周围散射体变化，同心半球体来对车辆周围散射体进行模拟。仿真结果表明，本文所建模型能够较好地模拟UAV-V场景信道模型，为UAV-V非平稳信道建模提供了新的理论参考。当前移动到移动通信系统中，主要使用车辆、无人机作为收发端，未来可以考虑向卫星或者新一代通信设备方向拓展，或者将研究环境设置得更为复杂。