复合材料层合板低速冲击损伤模拟及凹坑深度预测

李尹松，王 喆，柴亚南

(中国飞机强度研究所，陕西 西安 710065)

1 引 言

复合材料结构在制造、使用和维护过程中，容易遇到如工具坠落、跑道砂石等面外低能量冲击，这些冲击事件可能会造成层合板内部的分层、基体开裂和纤维断裂，危害结构的安全，而在层合板表面却仅留下勉强目视可见的损伤。凹坑深度是表征复合材料低速冲击损伤的重要变量，快速准确地预测复合材料层合板的冲击凹坑深度具有重要意义。

许多学者基于经典的Hertz接触模型对准静态压痕力和低速冲击作用下的凹坑深度进行了预测[1-4]。叶强等提出了一种考虑层合板性能退化的凹坑深度预测技术，对1.0mm以下的凹坑深度取得了很好的预测结果。李诗哲等建立了一种考虑分层响应的凹坑深度弹塑性演化模型，对翼盒壁板蒙皮在15J～45J能量冲击下的永久凹坑深度预测误差在10%以内。目前对凹坑深度的预测模型中，均采用基于半无限空间体的接触力-压痕深度公式，没有考虑层合板有限厚度的影响。

大量试验研究[5-7]表明，复合材料在准静态压痕力和低速冲击作用下产生的损伤具有等效性。闫丽等[6]发现，在拐点之前对应于冲击过程中的最大接触力的准静态压痕力产生的损伤面积、凹坑深度近似相等，这为采用准静态公式预测低速冲击凹坑的方法提供了依据。

本文将准静态压痕下的凹坑深度预测思路运用于冲击过程中，采用有限厚度修正的接触公式，结合有限元计算的冲击最大接触力和冲击区损伤面积，计算含损伤层合板的等效刚度，建立了一种冲击凹坑深度预测方法，并进行了两种铺层的层合板低速冲击试验，运用建立的方法计算预测了多种能量下的凹坑深度。

2 冲击凹坑深度计算方法

2.1 厚度修正的层合板接触理论

许多研究人员用横观各向同性材料半空间体的接触模型描述冲头与层合板之间接触力F和凹坑深度α的关系：

(1)

式中，r为冲头半径，ET为横观各向同性材料的等效弹性模量。

Wagih等[8]通过静压痕试验和仿真，对式(1)进行了有限厚度修正：

(2)

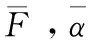
2.2 层合板等效工程常数计算

根据Turner的方法[9]计算层合板等效横观各向同性材料弹性模量ET：

(3)

其中：

(4)

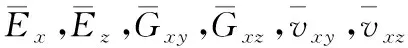
2.3 冲击区损伤刚度计算

接触力-凹坑深度关系与冲击区域的整体刚度相关。对含损伤的材料，可以通过损伤面积的大小反映损伤的严重程度。将冲击造成的损伤分为纤维损伤、基体损伤和分层损伤，通过各个模式的损伤面积定义折减系数：

(5)

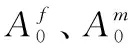
计算各个铺层的损伤工程弹性常数：

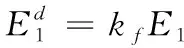
(6)

用折减后各铺层工程弹性常数计算各层损伤刚度矩阵，用式(3)、式(4)计算材料等效弹性模量ET，将最大接触力和等效弹性模量代入式(2)计算不同损伤状态下的凹坑深度。

3 低速冲击试验

低速冲击试验参照ASTM D7136/D7136M-07实施，试验装置使用中国飞机强度研究所自研的落锤低速冲击设备。试验件尺寸为150mm×100mm，材料为连续纤维增强聚合物基复合材料单向带，纤维为国产高强中模碳纤维，纤维面密度为145±5g/m2，层合板采用热压罐成型。试验件的铺层方式、铺层比例及名义厚度见表1。

表1 试验件铺层顺序

试验时，将试验件放置于125mm×75mm矩形开口的简支夹具上，上表面用4个橡胶夹头固定。采用直径16mm的半球形冲击头，通过调整冲击头高度调节冲击能量的大小，对试验件中心进行冲击。冲击后立即测量表面凹坑深度，并采用超声C扫描检测试验件内部的损伤状况。铺层方式为P1的试验件共18件，按6.7J/mm和9.7J/mm能量级各冲击6件，剩余6件进行BVID凹坑摸索冲击。铺层方式为P2的试验件共15件，分别按6.7J/mm、9.2J/mm、11.2J/mm、12.8J/mm和14.5J/mm能量级各冲击3件。

4 有限元分析

4.1 有限元模型

通过网格偏移的方法生成三维层合板模型，厚度方向每一个铺层生成一层网格，并在相邻两铺层之间添加零厚度层间单元用于模拟分层损伤，层间Cohesive单元采用二次应力准则判断损伤初始，采用BK准则模拟损伤演化。层内单元类型为C3D8R，层间单元类型为COH3D8。层内和层间单元材料属性设置如表2、表3所示。

表2 有限元模型材料属性(层内单元材料属性)

表3 有限元模型材料属性(层间单元材料属性)

冲头在冲击过程中的变形相较于试验件可以忽略不计，因此采用解析刚体建立半球形冲头模型，并设置质量参考点，赋予冲头5.65kg质量。

冲头与层合板之间设置通用硬接触，切向摩擦系数设为0.1。为保证接触过程中冲头垂直下落，限制冲头除沿垂直于平板方向外的其它所有自由度。为简化有限元模型，建模时略去背面支撑和上表面压头，使用相应的边界条件模拟夹具。如图1所示，分别限制平板4个角落节点的面内自由度(Ux,Uy)，平板背面沿开口区边缘限制节点的面外自由度(Uz)。

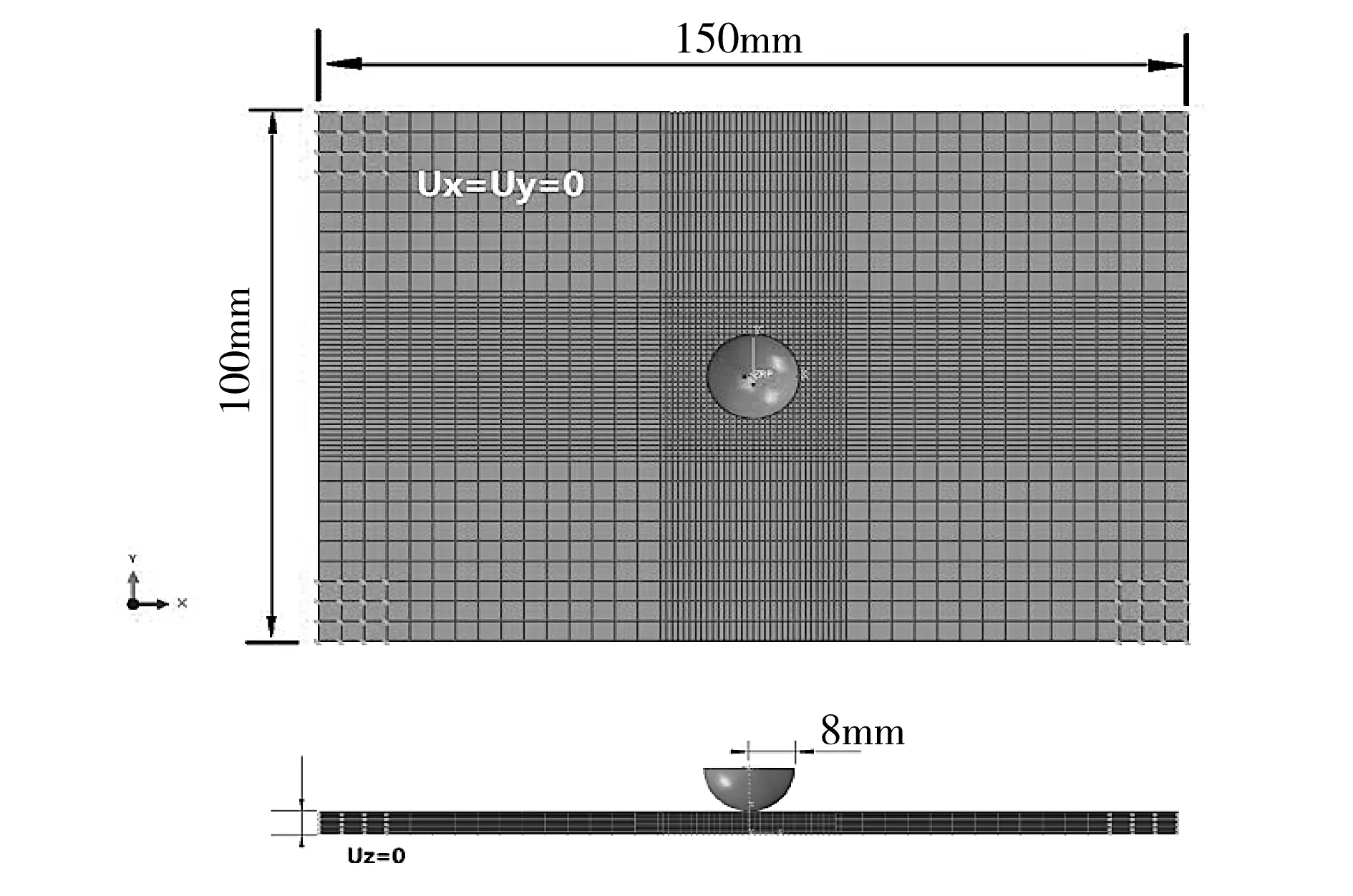
图1 复合材料层合板低速冲击有限元模型

4.2 材料失效模型及退化方案

选用基于应变表示的三维Hashin准则[10]判断层合板各层是否失效，各失效模式及判断准则如下：

(1)纤维拉伸(ε11≥0)：

(7)

(2)纤维压缩(ε11<0)：

(8)

(3)基体拉伸(ε22+ε33>0)：

(9)

(4)基体压缩(ε22+ε33<0)：

(10)

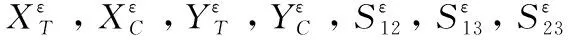
(11)

分别对满足式(7)-式(11)的失效单元进行材料参数退化，退化模型采用直接折减方法，具体折减方案如表4所示。

表4 各失效模式下的材料属性退化方案[1]

5 结果与讨论

5.1 损伤面积

图2给出了P1铺层方式下试样在3种冲击能量下的表面损伤形貌。由图可以看到，在37.5J时，损伤主要表现为基体开裂和表面层纤维劈裂；能量增大到55J时，表面纤维劈裂范围扩大；当能量增加至70J时，试样表面层产生纤维断裂，留下BVID凹坑，背侧纤维明显断裂、劈裂。图3所示为3种能量下的C扫内部损伤云图。

(a)37.5J (b)55J (c)70J图2 不同冲击能量下的损伤形貌

图3 不同冲击能量下的C扫损伤云图

提取有限元计算最大分层损伤面积，各冲击能量级下损伤面积的试验测量结果与有限元计算结果对比如图4所示。可以发现，分层损伤计算结果具有较高的精度。

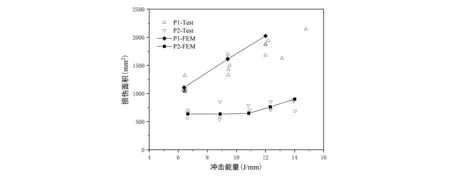
图4 损伤面积-冲击能量曲线

5.2 凹坑深度

未损伤状态下，P1、P2铺层方式的等效横观各向同性板工程弹性常数和ET的计算结果如表5所示，两种铺层各个冲击能量下最大接触力计算结果见表6。根据损伤面积计算各能量级(损伤状态)下的损伤等效弹性模量，将最大接触力和等效弹性模量代入式(2)计算凹坑深度，式(2)中的参数a,b,c,d参考文献[8]分别取0.5、1.35、0.05、0.8。凹坑深度计算结果与试验对比如图5所示。

表5 两种铺层的等效工程弹性常数

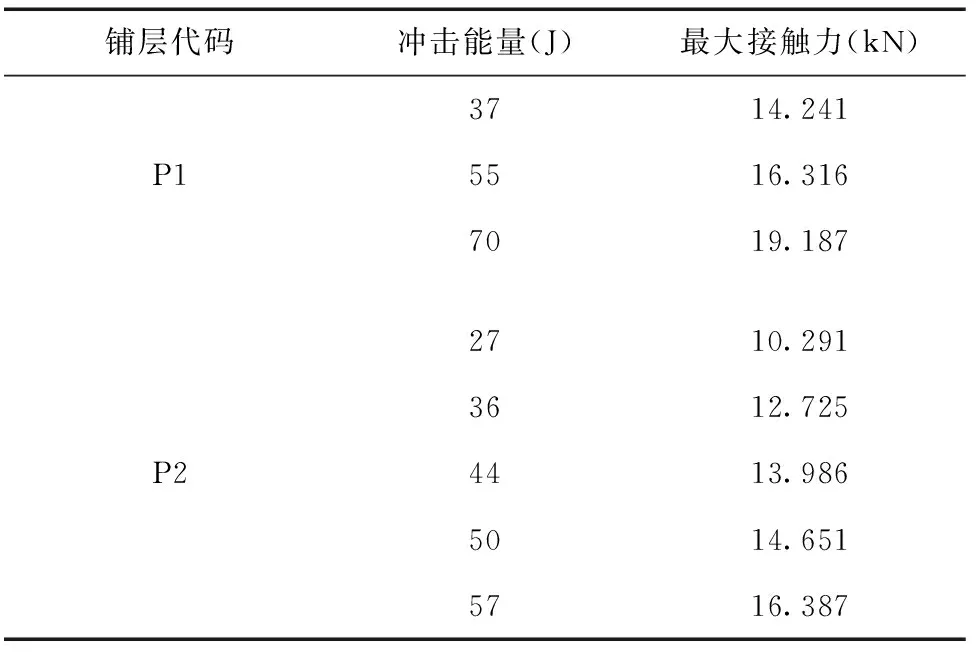
表6 各冲击能量下最大接触力计算结果

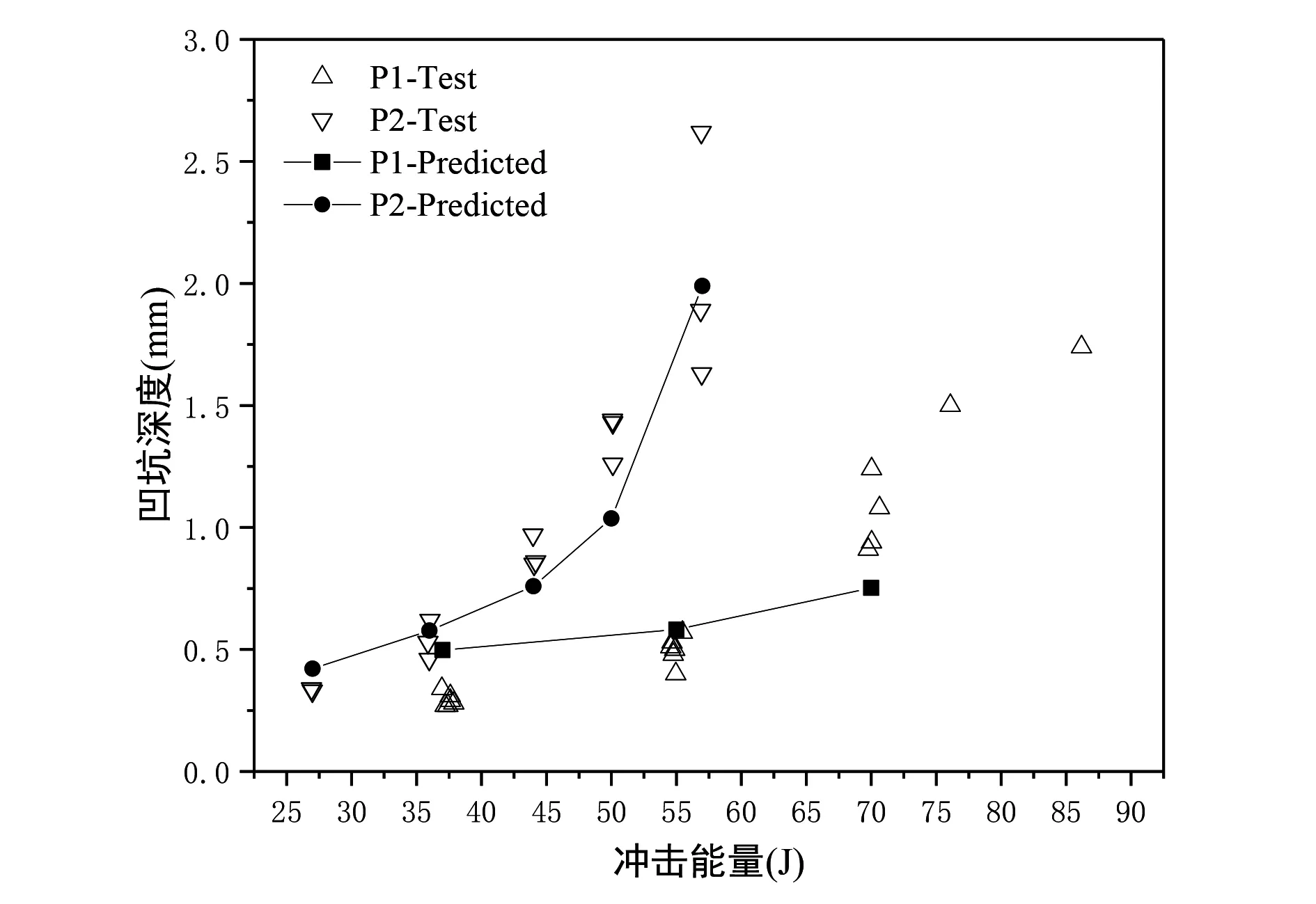
图5 凹坑深度-冲击能量曲线

从图中可以看出，两种铺层方式下凹坑深度随着冲击能量的增大而增加，同时，凹坑深度试验值的分散性也在增加。在高能量情况下，受冲击区域产生大量纤维断裂、基体开裂，已经基本失去继续承受冲击载荷的能力，分散性因此增大。对于两种铺层方式下的凹坑深度预测值，其变化趋势与试验值较吻合，其中铺层数较少的P2方式预测结果更好，并且在超过冲击拐点能量(35J)后仍有较高的精度。

6 结 论

基于准静态压痕力作用下的凹坑深度-接触力公式，建立了一种复合材料层合板低速冲击凹坑深度计算方法，结合有限元计算的最大接触力和损伤面积结果，能够对多种冲击能量下的凹坑深度进行预测。进行了两种铺层方式多种冲击能量下的层合板低速冲击试验和有限元分析，采用所提出的公式对两种铺层的凹坑深度进行了预测。有限元计算的损伤面积与试验测量值吻合程度较高，验证了有限元模型的有效性。凹坑深度预测结果基本能够反映其随冲击能量的变化，对于铺层数较少的薄板在拐点后的凹坑深度也有较高的预测精度。