高速动平衡机转子支承系统动力学特性研究

2022-09-27盛德恩孟庆慈

工程与试验 2022年3期

盛德恩，孟庆慈

(衡超装试(北京)科技有限公司，北京 100080)

1 引言

高速动平衡机是用于挠性转子动平衡测量与试验的设备，平衡的目标是使得在平衡机上平衡后的转子在其现场工作条件下，在直至其最高工作转速范围内的任何转速上，因不平衡引起的机械振动都在可接受的水平以下。挠性转子与刚性转子的根本不同在于其具有挠性，即在不同的转速上出现不同的挠曲变形，因此转子产生的不平衡离心力是随转速变化的。为实现高速动平衡机在整个转速范围内正确地测量振动信号并计算转子各校正平面上的不平衡量，转子支承系统的动态特性是十分关键的。由于此问题的专业性很强，目前的专门研究并不多。

文献[1]和文献[2]在挠性转子高速平衡方法一节中讲到：在某些情况下，希望平衡设备上使用的轴承支承条件和现场轴承支承条件相类似，以使转子在现场运行时的振型在平衡过程中能充分表现出来；在挠性转子的振型一节中指出，轴承及其支承的动力学性质和轴向位置对振型形状及转子的不平衡响应有很大的影响。这对高速平衡机转子支承系统提出了苛刻的要求。文献[3]是关于高速平衡设备的标准，对高速平衡机摆架提出了性能要求和检验方法，但摆架只是支承系统的一部分，高速平衡机的支承系统包括摆架、升高座(如果有)、床身及其支承结构等组成部分。文献[4]对机械支承座(即摆架)的设计计算给予了详细说明，但缺乏对床身和舱体的说明。

理论上讲，高速平衡机支承系统在转子的不平衡离心力激励下做强迫振动，为了正确测得反映转子不平衡特性的振动信号，最基本的要求是，在直至平衡机最高工作转速范围内，支承系统在测量方向(即径向)不允许存在固有频率。但怎样实现这一点，目前还没有明确的论述。文献[3]和文献[4]实际上都是假设床身与大地固连，刚度无穷大，但在许多情况下，这与工程实际是有一定出入的。在隧道式真空防爆舱结构中，床身下面的支承钢结构的弹性变形不能忽略，其参数是需要正确设计和施工的。近年来国内多台高速平衡机由于支承系统设计不当而出现问题，设备不能达到预期的性能指标，因此对该问题的研究具有重要和现实的意义。

2 支承系统的动力学模型

对于较小规格的高速平衡机，其支承摆架通常是直接紧固在与地基浇筑为一体的床身上的，这时可将床身视为地基，只需分析摆架杆簧与轴承座组成的单自由度振动模型就可以了，摆架设计只要求该系统的固有频率高于摆架最高工作转速频率就行了，实际中比较容易实现。

对于较大规格的高速平衡机，通常采用隧道式真空防爆舱，床身下面通过一定的支承结构与基础固连，摆架安装在床身上，这时支承结构的弹性变形便不能忽略，相当于摆架支承在弹性结构上。还有一种情况是在大规格舱体内安装较小规格的摆架，这时需要在摆架下面增加一个增高座，以得到相同的中心线高度，这个增高座的弹性变形往往也不能忽略。这两种情况下支承系统的动力学模型便不能简化为单自由度振动系统，即使只分析在一个方向上的振动，比如垂直方向，也至少应该按二自由度振动系统考虑。二自由度振动模型如图1所示。

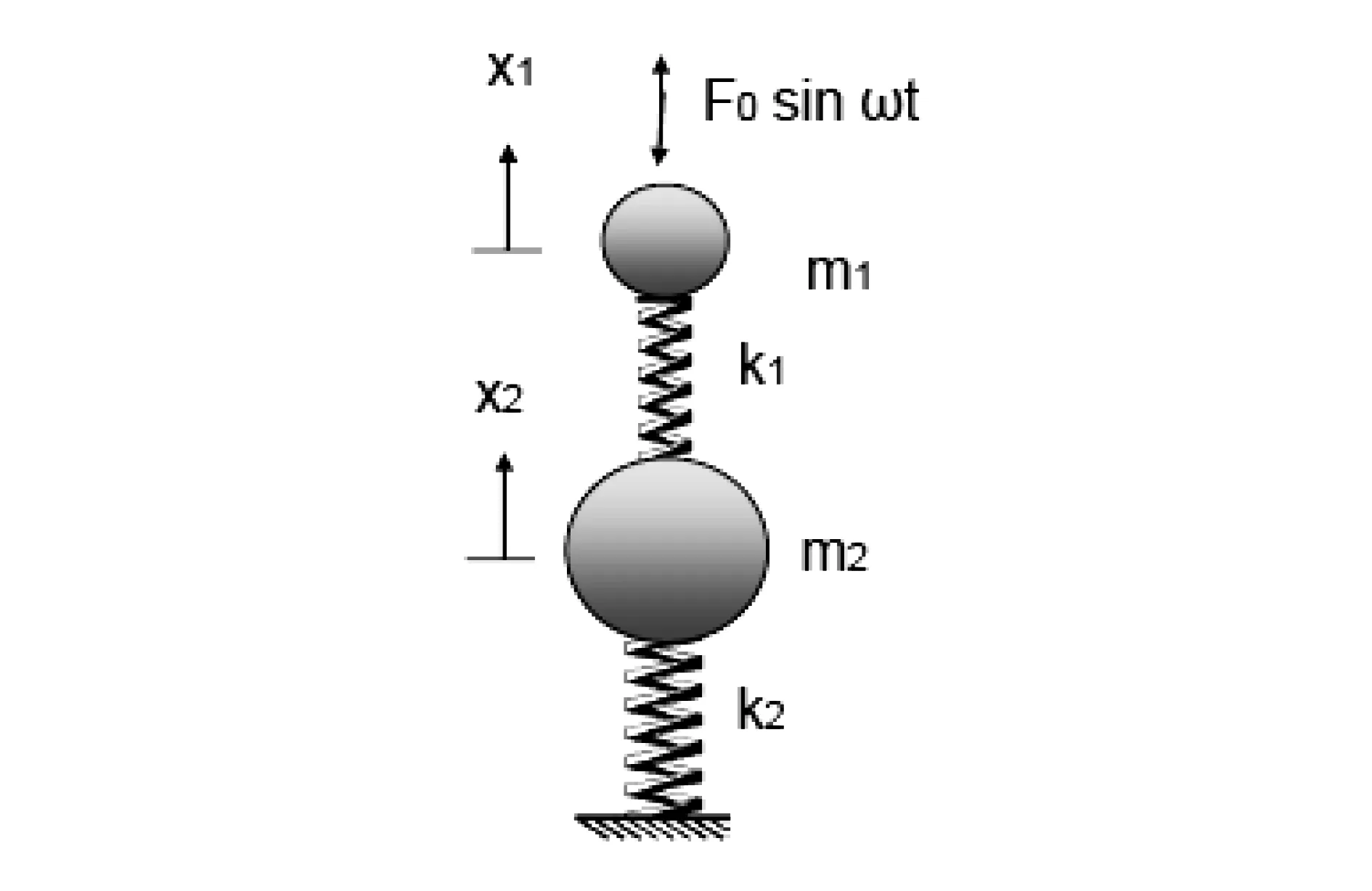
图1 二自由度振动模型

设摆架轴承座质量为m1，摆架杆簧刚度为k1，摆架体质量为m2，其下部结构的刚度为k2。轴承座上受不平衡离心力作用，在垂直方向表现为交变的强迫激励F0sinωt，其动力学方程为：

(1a)

(1b)

设方程组的解x1(t)=X1sinωt，x2(t)=X2sinωt，则得到关于二质量振动幅值X1、X2的二元一次线性方程组：

-ω2m1X1-k1X2+k1X1=F0

(2a)

-ω2m2X2+(k1+k2)X2-k1X1=0

(2b)

其行列式形式为：

(3)

其系数行列式的值为：

(4)

两质量体的振动位移为：

(5a)

(5b)

式中，Δ为分母，当其为0时，振幅将无穷大，此时的ω值为系统的固有角频率。令式(4)Δ=0并整理得系统的特征方程：

m1m2ω4-(k1m1+k2m1+k1m2)ω2+k1k2=0

(6)

这是一个关于ω2的一元二次方程，用求根公式便可求出其两个根，即两阶固有频率，仅对其中较低的一阶固有频率感兴趣，即：

(7)

该公式的实际意义在于，当摆架的轴承座质量m1、杆簧刚度k1和摆架体的质量m2已知后，便可估算床身所应具备的刚度，为床身支承结构刚度设计提供依据。

实际中常见的摆架传感器测量的是摆架轴承座的相对振动，即轴承座相对于摆架体的振动：

(8)

从该式可以观察到一个奇特的现象，当激励频率趋近于摆架体与下部支承结构组成的弹簧质量系统的固有频率，即k2-ω2m2=0时，相对振动幅值趋近于0，两质量同步振动，宛如摆架刚度k1为无穷大。

上述二自由度模型显然是过于简化的振动模型，但通过对其分析，仍能看出一些一般性的问题。第一，由于摆架下部支承结构的刚度是有限的，支承系统的一阶固有频率会低于摆架自身的固有频率；第二，当激励频率等于下部结构自身的固有频率时，相对振动幅值趋近于0，出现相对刚度无穷大的奇特现象。

为了更准确地分析摆架的振动，应采用图2所示的五自由度模型。系统有5个独立的坐标，摆架轴承座质量mb的垂直和水平位移，摆架体质量mp的垂直和水平位移，还有摆架体作为刚体，其转动惯量为Jp的转角。这是个复杂的模型，不能给出解析解。

图2 摆架五自由度振动模型

3 实例分析

某摆架最大承载4.5t，设计最高工作转速20000r/min，回转直径1300mm，通过增高座将其安装在80t的大规格高速平衡机舱体内，回转直径增加到4000mm，舱体床身和增高座刚度都会成为影响整个支承系统动态特性的因素，影响摆架的最高工作转速。针对该摆架进行了全转速激振试验，将激振器安装于轴承座轴孔中，除了测取摆架相对振动传感器信号外，还在轴承座垂直和水平方向以及摆架体两侧的垂直和水平方向加装了振动传感器，如图3所示。

图3 小规格摆架安装于大舱体内的激振试验

图4所示是激振试验时摆架相对振动传感器测得的在2000r/min～10000r/min转速段的振动速度有效值(单位mm/s)和相位(单位°)(纵轴)随转速(横轴)的变化。振动幅值在整体上呈三次抛物线形态，相位呈直线形态，这都是正常的和所希望的。但是，振动速度有效值在8453r/min出现“异常”峰值0.89mm/s，随后急剧下降，在8701r/min出现“异常”谷值0.15mm/s；一直平坦的相位在8651r/min左右突降了约100°，出现了“异常”波谷。摆架在操作侧和非操作侧共有两个这样的传感器，相对于垂直轴成45°安装，两个传感器信号近似，不平衡解算用的是这两个传感器信号的合成信号。可以推知，合成信号在这个转速区间也会出现幅值“异常”峰、谷以及相位“异常”谷。

图4 摆架相对振动幅值与相位

摆架是成熟的产品，设计最高工作转速为20000r/min，出厂前做过检验。很显然，在这个转速区域的振动“异常”不是缘自摆架自身，而是支承系统的其它环节。

在摆架体两侧垂直和水平方向的传感器信号在该转速区域也出现了振动峰值和相位变化。图5所示为操作侧垂直方向在2000r/min～10000r/min转速段的幅值和相位。横轴是转速(单位r/min)，纵轴是振动速度有效值(单位mm/s)和相位角(单位°)。由图可见，在转速8552r/min点有振动峰值4.04mm/s，相位在此转速段有180°的翻转，是典型的过共振区特征。

图5 摆架体振动幅值与相位

在摆架体上的其它3个传感器信号也都呈现相同的现象，摆架加上附加刚度后测试得到的结果也相似。这些证据说明，该转速段的“异常”振动是摆架下部结构(增高座和床身支承结构)的刚度不足引起的共振。

在10000r/min以上范围发现了更多的这样的共振峰现象。显然，该摆架在8000r/min以上是不能正常工作的。

同一台高速平衡机上还配置有一对承重50t的摆架，其设计最高工作转速为6000r/min，摆架底部宽度跨越到了床身，因此增高座的影响可以忽略，下部支承结构的问题主要来自于床身支承结构。该摆架激振试验读取的是摆架两传感器的合成信号，即摆架轴承座垂直方向的相对振动。全转速范围激振试验振动速度有效值(单位μm/s)和相位(单位°)如图6所示。振动信号幅值和相位在5000r/min转速以下基本正常，但随后幅值出现了峰值，并且峰值过后大幅下降，相位信号在此出现了约300°的突变。加上摆架附加刚度后的情况类似。所以，此处幅值的峰值和下降与前面所述的“异常”峰谷是同一现象。如上文所分析，这不是摆架自身系统共振，而是摆架下部结构共振。两规格摆架的激振测试结果可以说明，该平衡机床身支承结构刚度不够。

图6 50t摆架轴承座相对振动幅值与相位

高速平衡机现场激振试验的主要目的是整台机器的性能检验，其中最重要的参数是测试出支承系统的动刚度。在激振器不平衡量已知的条件下，测得不同转速下摆架轴承座相对振动幅值(通常为振动速度有效值)，就可以通过计算得到激振力和振动位移幅值之间的比值，即摆架的(相对)动刚度。理想情况下，在整个转速范围内，其应该是一条由高到低的光滑曲线，下降到0值的转速高于最高工作转速。如果支承系统有问题，则曲线形状异常。图7是根据图6数据计算出的动刚度曲线，纵轴是刚度(单位N/μm)，横轴是转速(单位r/min)。可以看出，在5000r/min转速之上刚度值已经非常低了，接近0后又突然增加，甚至超过了左端的静刚度值，这是床身下部结构共振的典型特征。