模糊数列关于序β的f-理想统计收敛和强f-理想收敛
2022-09-27巩增泰
冯 雪, 巩增泰
(1. 青海民族大学 数学与统计学院, 青海 西宁 810007; 2. 西北师范大学 数学与统计学院, 甘肃 兰州 730000)
本文基于模函数f将统计收敛和强收敛置于理想的框架下,提出和研究了模糊数列关于序β的f-理想统计收敛和强f-理想收敛,推广了前人的工作.
1 定义及说明
实数R上的模糊集u称为模糊数,是指:u是正规的、凸模糊集、隶属度函数u(x)上半连续、支撑集[u]0=cl{x∈R:u(x)>0}为紧集.记所有模糊数所组成的集合为E1.对任意的0≤r≤1,水平截集[u]r={x:u(x)≥r}是一个闭区间.对u,v∈E1,k∈R,加法和数乘为:
[u+v]r=[u]r+[v]r,
[ku]r=k[u]r.
模糊数u,v∈E1之间的距离为
其中D表示Hausdorff距离,分别是[u]r和[v]r的左右端点.表示零模糊数.
记N是全体自然数组成的集合,集合A⊆N的自然密度定义为
设f是无界模函数,β∈(0,1],设N是全体自然数组成的集合,集合A⊆N的fβ-密度定义为
δf
当f(x)=x且β=1时,
δf
若函数f:[0,∞)→[0,∞)是连续的递增函数,且f(0)=0,对x,y≥0,有
f(x+y)≤f(x)+f(y),
则称函数f是模函数[9].
定义 1设x={xk}为模糊数列,x0为模糊数,f为无界模函数,β∈(0,1],若对任意的ε>0,δ>0,有
D(xk,x0)≥ε}|)≥δ}∈I,
注 1若对所有的n∈N,当f(x)=x且β=1时,退化为其中,
例 1设I是自然密度为0的自然数集N的理想,A={12,22,…},定义模糊数列
x
即模糊数
即
δ}⊂A∪{2,3,…,M}∈I.
由以上讨论可知,当n∈A且n→∞时,
定义 2设x={xk}为模糊数列,f为无界模函数,β∈(0,1],对任意的δ>0,定义下列强f-理想收敛的模糊数列空间:

其中

注 2若称模糊数列x={xk}关于序β强f-理想收敛于模糊数x0;若称模糊数列x={xk}关于序β强f-理想收敛于模糊数列若称模糊数列x={xk}关于序β强f-理想有界.
注 3若对所有的n∈N,当f(x)=x且β=1时,模糊数列空间退化为其中
2 模糊数列关于序β的f-理想统计收敛的相关性质
定理 1设x={xk},y={yk}是两个模糊数列,则以下成立:
1) 对任意实数C,若x则
2) 若x且y则xk+y
证明1) 当C=0时,结论显然成立.
设C≠0,有
因为
D(Cxk,Cx0)≥ε}|)≥δ}⊂
D(x
压力注浆孔的布置就是超前探水孔的布置位置,根据该掘进段实际情况,如渗涌水量较大,可在适当位置增加注浆孔的数量,以确保防治水效果。
D(xk,x0)≥ε}|)≥δ}∈I,
D(yk,y0)≥ε}|)≥δ}∈I.
因为
D(xk+yk,x0+y0)≤
D(xk+yk,x0+yk)+D(x0+yk,x0+y0)=
D(xk,x0)+D(yk,y0),
对任意ε>0,有
由
D(xk+x0,yk+y0)≥ε}|)≥δ}⊂
可得
xk+y
定理 2设模糊数列x={xk}与关于序βf-理想统计收敛的模糊数列y={yk}几乎处处相等(即集合{k∈N:xk≠yk}为有限数集),则x={xk}关于序βf-理想统计收敛,且与y={yk}收敛于同一模糊数.
证明对几乎所有k,有xk=yk且y对于任意ε>0,有
{k∈N:xk≠yk},
所以
定理 3设β、γ是两实数,且满足0<β≤γ≤1,那么
证明设x={x则
由上式可知
D(xk,x0)≥ε}|)≥δ}⊆
D(xk,x0)≥ε}|)≥δ}∈I,
推论 1设x={xk}为一模糊数列,β∈(0,1],那么其中
3 模糊数列关于序β强f-理想收敛的相关性质
定理 4强f-理想收敛的模糊数列空间有如下包含关系成立
证明显然成立.
设x={x则
定理 5设f1,f2是模函数,则以下结论成立:
证明设则因此,对任意的δ>0,β∈(0,1],有
那么
因此可以得到
f2(D(x
故
2)和3)的证明与1)相似.
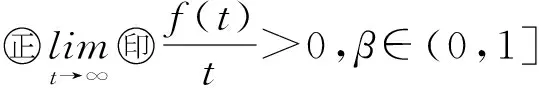
证明设x={x记那么f(t)≥lt,t≤l-1f(t),所以,
由
可以得到
定理 7设β,γ是两实数,且满足0<β≤γ≤1,那么
证明设x={x则
于是可知
4 模糊数列关于序β的f-理想统计收敛和强f-理想收敛的关系
定理 8设f为模函数,若存在正数C,使得对所有的x≥0,y≥0,有f(xy)≥Cf(x)f(y),并且0,则
证明因为
f(|{k≤n:D(xk,x0)≥ε}|ε)≥
Cf(|{k≤n:D(xk,x0)≥ε}|)f(ε),
那么
所以
因此x={x故
5 结论
致谢青海民族大学2021年校级青年项目(2021XJGH24)对本文给予了资助,谨致谢意.
