基于滑窗自适应的故障估计与补偿及其在组合导航系统中的应用

罗治斌，刘永峰，宋 欣

（1.中国西南电子技术研究所，成都 610036；2.空军装备部成都局业务处，成都 610036；3.哈尔滨工程大学智能科学与工程学院，哈尔滨 150001）

1 引 言

惯性导航系统（Intertial Navigation System,INS）和卫导（Global Position System,GPS）相结合的INS/GPS 系统是飞行器中重要的组合导航系统。在它们共同作用下，可提高导航性能[1-3]。如何在高速飞行的飞行器上，利用故障检测算法精准和快速地检测出故障是保障飞行安全的关键[4]。因此，众多学者在故障检测领域开展了大量的理论和实践工作。

由于其在动态系统故障诊断中的有效性，基于模型的检测方法已经取得了显著的发展[5-6]。此外，基于模型的故障检测可分为基于观测器的确定性模型方法和基于滤波的随机模型方法[7-8]。

考虑到系统的随机性和易于利用的统计特性，基于滤波器的方法受到了广泛的关注[9-10]。简而言之，基于滤波器的方法先对系统状态进行估计，然后得到残差信号进行故障检测。广义似然比方法是在该结构下较早为人所知的故障检测方法之一。此后，可以在文献[11-12]中找到许多扩展。与故障检测相比，故障估计更具挑战性，因为它可以提供更多的信息，包括故障的大小和形状[13]。为了实现故障估计，通常对卡尔曼滤波器（Kalman Filter,KF）进行改进，以估计故障的幅度和形状[14-15]。例如，通过将随机系统划分为两个子系统，设计了降阶KF 近似执行器故障[15]。虽然在文献[15]中给出了故障信号的估计，但无法得到状态估计。因此，解决这一问题的不同方法已经发展出来了[16-19]。针对文献[16]中线性系统的随机偏置（故障）问题，提出了一种两级卡尔曼滤波器（TSKF），并将其推广到文献[17]中具有未知输入的状态估计和故障估计。近年来，针对多智能体系统[18]实现了一种状态和故障同时估计方法以及二维系统[19]。

上述基于滤波器的方法考虑了线性高斯状态空间模型所描述对象的故障估计问题。在这些方法中，噪声统计量和故障系数矩阵都是假定已知的，这极大地限制了它们的实际应用。最近，变分贝叶斯（Variational Bayes,VB）算法被用来估计状态估计中的未知噪声统计量[20-23]。例如，在文献[20]中开发了一种自适应KF 来估计高斯噪声的协方差，在文献[21]中提出了一种鲁棒滤波器来估计学生t 分布噪声参数。此外，文献[22-23]中噪声的未知统计量采用高斯分布或逆Wishart分布估计。然而，这些方法应用较少，无法解决故障估计领域中未知故障系数矩阵的问题。

针对文献[20-23]中已成功估计出未知噪声统计量的问题，为了进一步提高自适应性能，提出了一种新型滑动窗口变分自适应故障估计的思想。它由前向KF 和后向卡尔曼平滑（Kalman Smoother,KS）组成。前向KF 基于噪声协方差矩阵的先验估计计算在线状态估计。同时，后向KS算法通过在线状态估计为滑动窗口状态向量提供了一个近似平滑的后验概率密度函数。在此基础上，利用滑窗变分自适应滤波方法对故障噪声协方差矩阵和量测噪声协方差矩阵的后验概率密度函数进行了解析更新，实现了对滑动窗口故障信号的在线估计。该算法避免了不动点迭代，具有较好的计算效率。仿真结果表明，该方法具有较好的滤波精度和一致性。具体而言，本文的贡献归纳如下：（1）提出的方法采用随机过程描述传感器故障动态，从而可以通过滑窗变分自适应滤波技术框架对传感器故障进行估计。（2）与现有的故障估计方法不同，该方法可以在不知道量测噪声协方差和故障系数矩阵的情况下，通过设计滤波器来估计传感器的故障，从实际应用的角度来看具有优势。也可以在传感器故障的同时估计系统状态，获得满意的估计精度。

2 传感器建模

2.1 组合导航系统模型

根据捷联惯导系统以及惯性器件的误差方程对系统量测值的影响，组合导航系统的状态方程表示为：

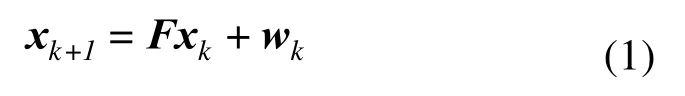
系统的状态量选取为：

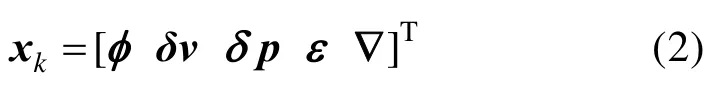
式中，xk是SINS 误差状态向量，F是状态转移矩阵，wk是系统噪声向量。φ=[φEφNφU]T分别为惯性平台的三个误差角，δv=[δvE δvNδvU]T分别表示东北天方向上的速度误差，δp=[δpEδpNδpU]T分 别是 纬度、经 度和高度上的误差，ε=[εxεyεz]T表示陀螺的常值误差，∇=[∇x∇y∇z]T表示加速度的常值误差。

状态转移矩阵为：

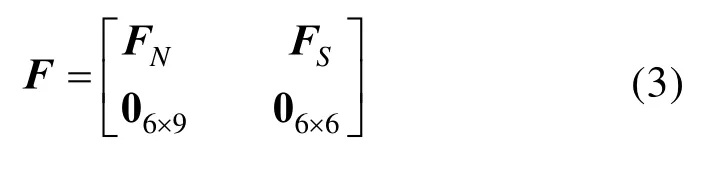
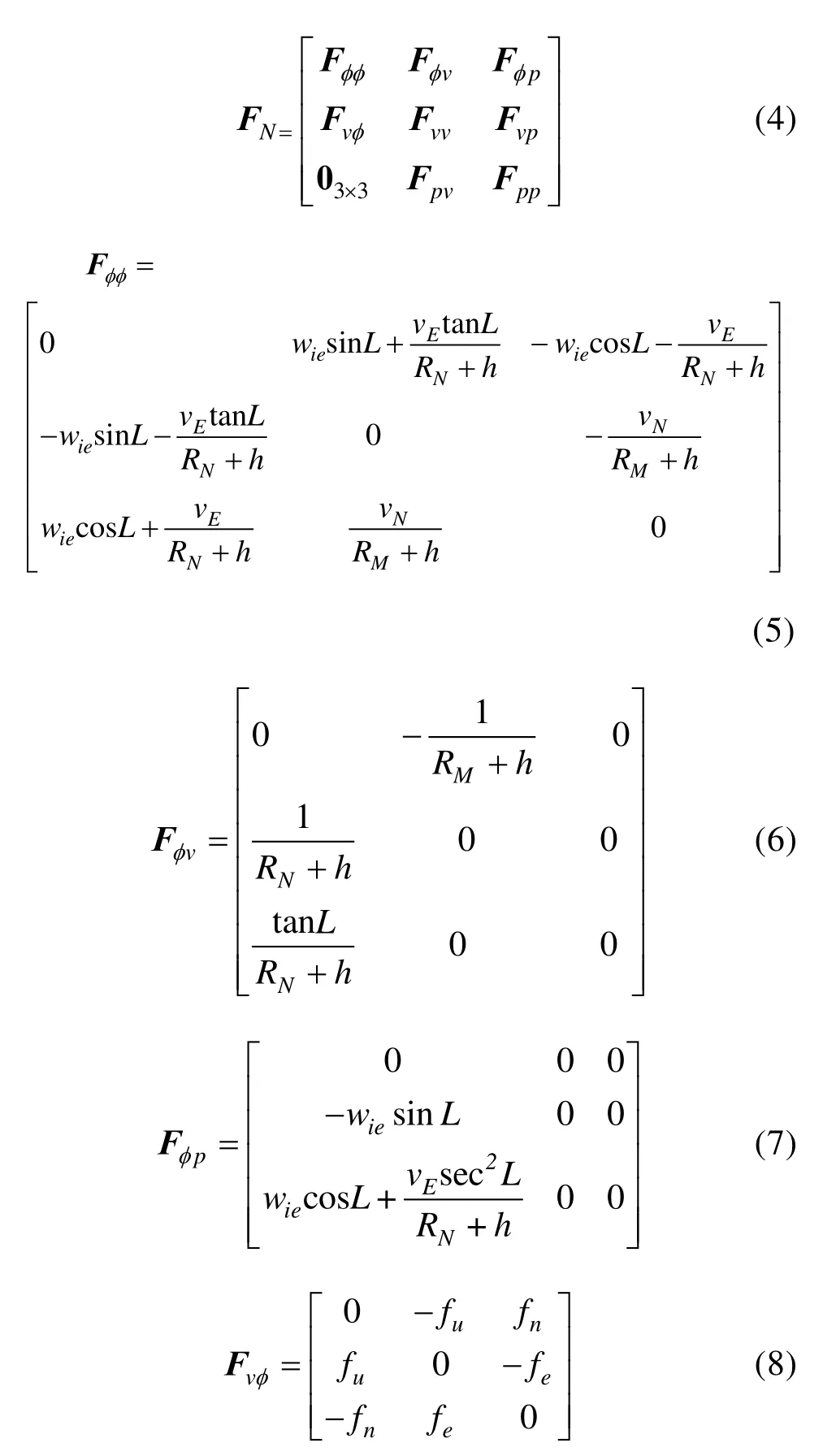
式中，FN表示惯导系统的误差模型。

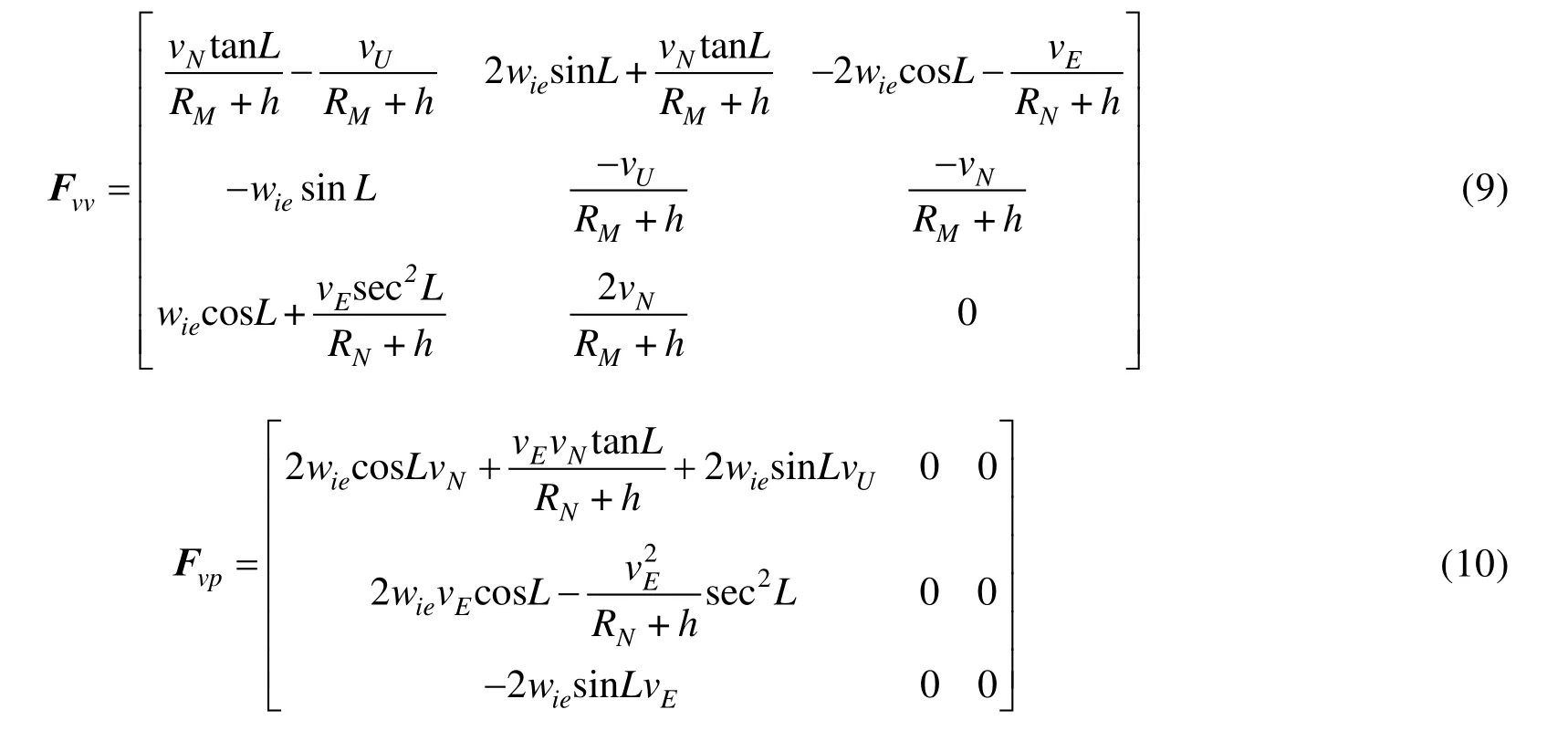
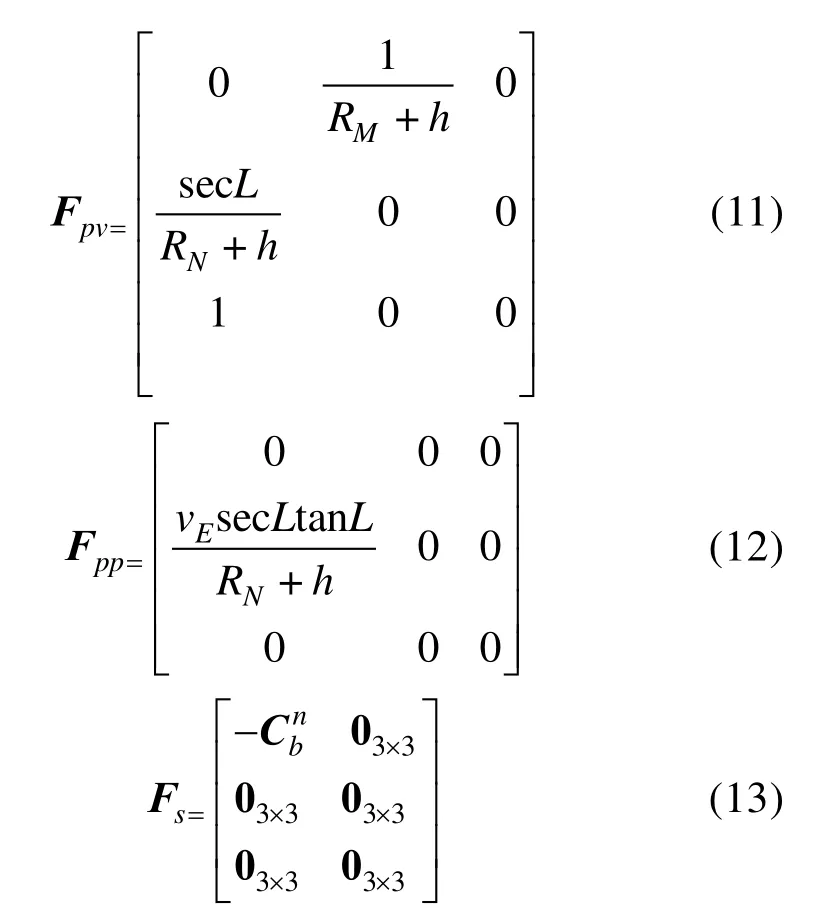
SINS/GPS 采用容易实现的松组合方式，GPS接收机可以一边辅助惯性导航系统，一边保持独立工作。惯性导航系统与GPS 输出的速度、位置信息之差作为量测信息，得到惯性导航系统的误差的估计值。

定义位置量测方程为：

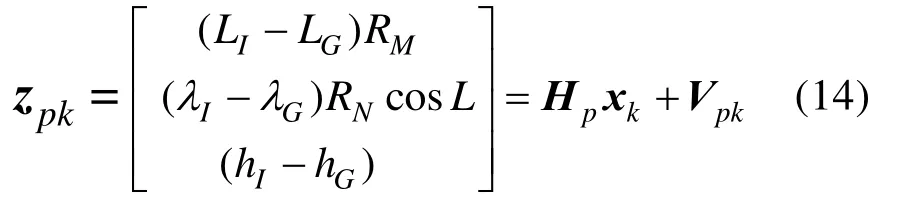
式中，zpk代表 GPS 与 INS 的位置之差。RM和RN分别为地球子午圈和卯酉圈半径；ξLG、ξlG、ξhG为接收机的位置误差。

定义速度量测方程为：

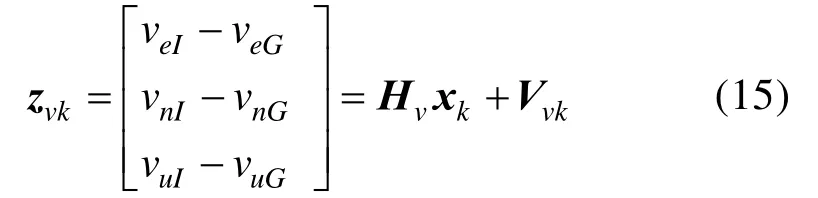
式中，Hv=[03×3diag[1 1 1]03×9];Vvk=[ξeGξnGξuG]T；ξeG、ξnG、ξuG为GPS 接收机沿东、北、天方向的测速误差。

联合速度和位置量测方程，SINS/GPS 组合导航的量测方程为：

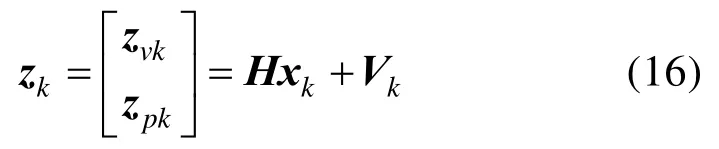
假设初始状态向量x0服从高斯分布，即

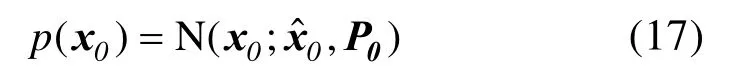
在传统的基于KF 的故障检测方法[10-11]中，计算新息ςk来检测故障信号：

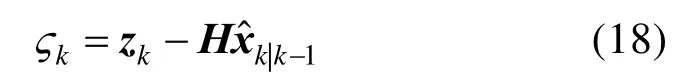
如前所述，基于KF 的故障检测方法的实现不能提供一些具体的故障信息，如故障值的大小。另一方面，基于滤波器的方法将传感器故障时的测量方程描述为[16-19]：

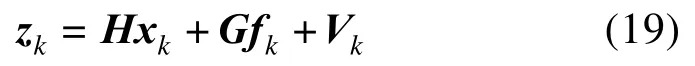
式中，fk为传感器故障；G为相应的故障系数矩阵，通常假设故障系数矩阵是已知的。然而，在实际应用中，G是不确定的。系统在正常状态下，Rk不会有任何突变。因此，本文所提出的算法是通过监测Rk的变化来检测出传感器的故障，该算法的具体实现如下所述。

2.2 传感器故障建模

为了提供传感器故障fk的鲁棒估计，我们认为fk可以被描述为一个随机过程

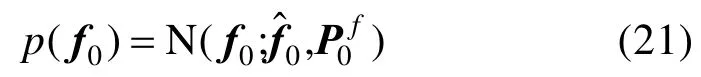
为了描述潜在的故障场景，测量方程(2)可以改写为：

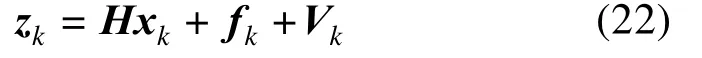
式中，Vk为满足Vk=N（ 0,Rk）的量测噪声。这里，Rk的确切值是未知的。因此，新的状态空间模型由式(1)(19)(20)组成。与状态向量xk相似，fk也可以由模型(20)和式(22)估计出来，fk的后验描述为

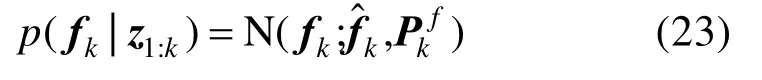
式中，fk和Pkf分别为故障向量及其相应估计误差协方差的均值。要用所构建的模型来估计故障，Rk需要已知[16-17]，这通常是不可能的[20-21]。为了解决这个问题，本文使用滑窗变分自适应算法来估计Rk。

3 使用滑窗自适应滤波估计故障

为了验证提出的想法，首先在算法1 中回顾了标准KF 和KS。由算法1 可知：

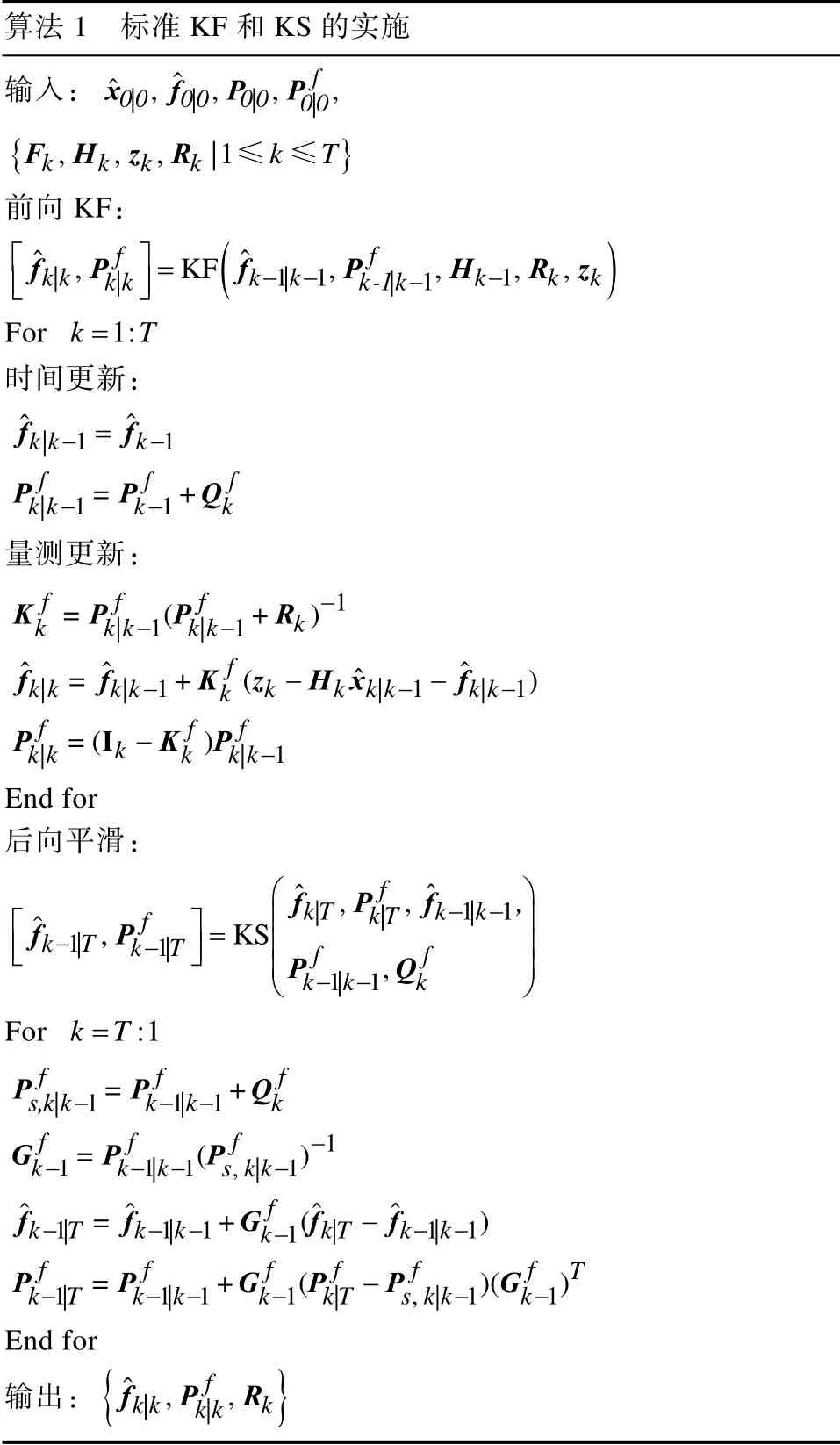
算法1 标准KF 和KS 的实施输入：xˆ 0|0,fˆ0|0,P0 |0,P0|f0,{Fk,H k,z k,Rk |1≤k ≤T }前向KF：■■ fˆ k|k,Pkf|k ■■=KF （ fˆ k -1 |k-1,Pkf-1|k-1,Hk-1,Rk,zk）For k=1:T时间更新：fˆ k | k-1=fˆk-1 Pkf|k-1 =Pkf-1+Qkf量测更新：Kkf=Pkf|k-1 (Pkf|k-1+Rk)-1 fˆ k|k=fˆ k|k-1+K kf (zk-H k xˆk|k-1-fˆk|k-1)Pkf|k=(I k-K kf)Pkf|k-1 End for后向平滑：■■fˆ k-1 |T,Pkf-1|T ■■=KS■■■■■P fˆ k k f|-T 1|,k P-k1 f|,TQ,kffˆk -1 |k-1,■■■■■For k =T:1 Ps,fk|k-1 =Pkf-1 |k-1+Qkf Gkf-1 =Pkf-1 |k-1 (Psf,k|k-1)-1 fˆ k-1 |T=fˆ k-1 |k-1 +Gkf-1(fˆ k|T-fˆk -1 |k-1)Pkf -1 |T=Pkf -1 |k-1 +Gkf-1 (Pkf|T-Ps f,k|k-1) (Gkf-1)T End for输出：{ fˆ k|k,Pkf|k,Rk}

我们的关键思想是通过在线估计量测噪声矩阵Rk来捕获故障信号，使用滑动窗口测量值zk-L:k从时刻K-L到时刻K，在此基础上将实现滑窗变分自适应滤波。其中，L表示窗口长度。提出的滑窗变分自适应滤波包括3 个步骤：正向KF、后向KS 和噪声矩阵的在线估计。

在前向KF 中，故障信号在K时刻的后验概率函数p(fk|z1:k)可以近似为：

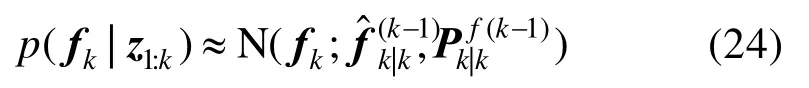
式中，和分别表示近似滤波估计和误差协方差矩阵和并且是由 KF()求得的，表示的是K-1时刻估计的故障噪声协方差矩阵和量测噪声协方差矩阵。

在后向KS 中，在时间间隔[K-L,K]处滑动窗口平滑后向概率密度函数近似为

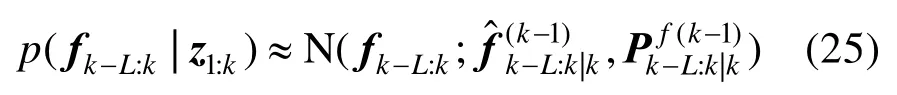
利用该方法得到了噪声矩阵在K时刻的近似估计，为了实现所提出的思想，需要在线联合推断滑动窗口状态向量fk-L:k和量测噪声。为此，将在线计算后验概率密度函数p(fk-L:k,Rk|z1:k)。

注1：由于在实际应用中噪声矩阵通常是缓慢变化的，所以当前的概率密度函数可以由先验噪声估计获得。虽然这种近似可能会给后验概率密度函数带来较小的误差，但可以显著降低计算复杂度。

为了在线计算p(fk-L:k,Rk|z1:k)，需要选择一个近似的模型。考虑到在实际应用中故障噪声矩阵和量测噪声矩阵变化十分缓慢，假定所有的噪声矩阵在时间间隔[K-L,K]内是近似Rk的。同时，在时间间隔[K-L,K]内，量测似然概率密度函数可以写成：

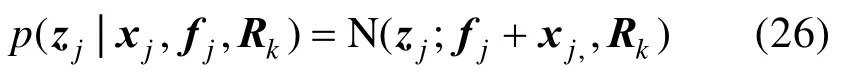
对于具有已知均值的向量的高斯分布，其协方差矩阵的共轭先验概率密度函数通常被建模为IW[14-15]，因此协方差矩阵Rk的先验分布也被建模为IW，以保证共轭推理，即

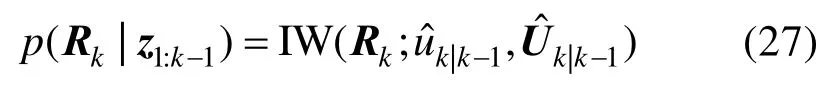
式中，和是p(Rk|z1:k-1)的自由度参数和逆尺度矩阵，将在下面进一步确定。

一般来说，在工程实践中，没有可用的模型来描述自由度参数和逆尺度矩阵的变化，但自由度参数和逆尺度矩阵往往表现出缓慢的变化。基于此，他们当前时刻的先验概率密度函数应该与前一个时刻的后验概率密度函数具有相同的均值。但由于演变模型的未知，先验概率密度函数的不确定性略有变化。为此，我们在文献[11]中采用了类似的方法，通过ρ和先验参数和近似噪声协方差矩阵的近似后验概率密度函数，分别表示为：

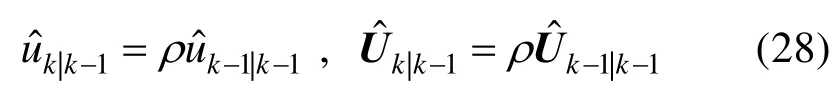
式中，ρ是遗忘因子，用来描述故障噪声协方差矩阵和量测噪声协方差矩阵随时间的波动。为了保证滤波器的准确性和稳定性，我们建议将ρ设置为0.9～1。接下来，根据式(4)～(6)中提出的模型，利用VB 方法计算p(fk-L:k,Rk|z1:k)。

根据标准VB 方法，假设故障信号与噪声协方差矩阵相互独立，则将p(fk-L:k,Rk|z1:k)近似为如下形式：

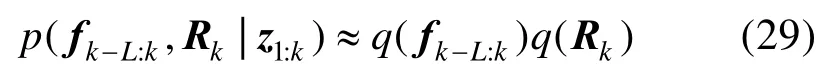
式中，近似的后验概率密度函数q(θ)满足如下统一的方程：

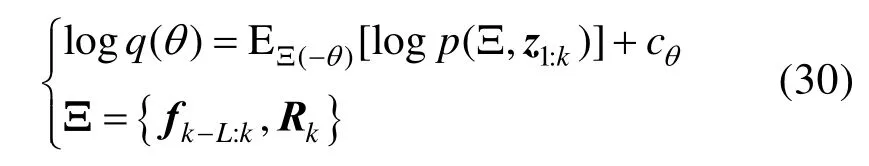
式中，θ表示集合中的任意成员；Ξ(-θ)表示除θ之外的集合Ξ 中的任意成员；cθ是一个常数，与变量θ无关。

从式(29)～(30)可以看出，变分参数fk-L:k和Rk是相互耦合的，通常采用不动点迭代法求得近似解[17]。然而，这样的迭代将导致大量的计算复杂性。在本文中，为了避免迭代和提高计算效率，对q(Rk)进行了分析更新。根据式(24)，我们提出将q(fk-L:k)近似为：

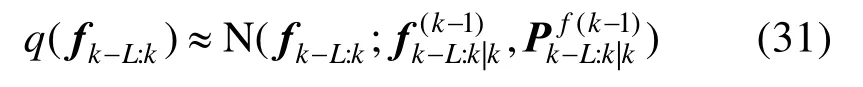
命题1：利用式(29)～(31)将Rk的后验概率密度函数更新为IW 分布，即

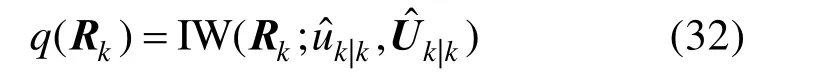
式中，参数和可以由如下计算得到：

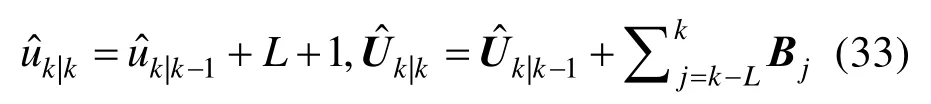
式中，辅助矩阵Bj表示如下：

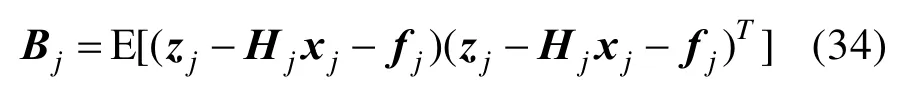
命题1 的证明与我们之前的工作[13]相似。利用式(28)计算式(31)中的数学期望为：

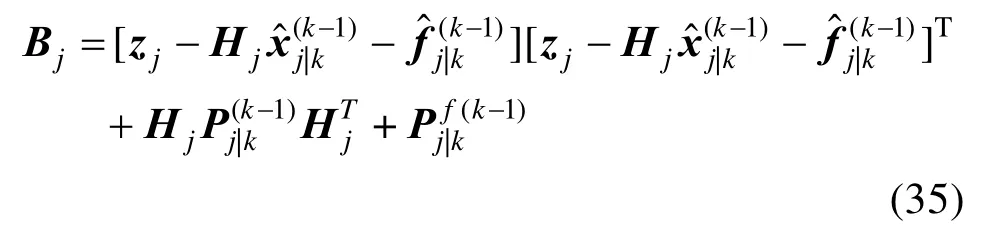
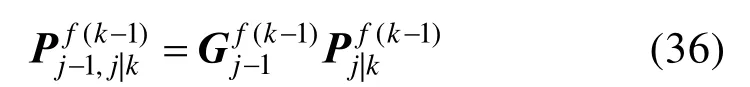
式中，是j-1时刻的平滑增益。

根据命题1，Rk的计算方式如下：

算法2 滑窗自适应滤波的一步预测执行输入：{ fˆ j(|jj-1),Pj|f j( j-1)|k-L ≤j ≤k-1},ρ,uˆ k-1 |k-1,U ˆ k-1 |k-1,Rˆk-1,{Fj,Hj,zj |k-L≤j ≤k}.前向滤波：1.■■fˆ k(| k k-1 ),Pk f-1(| kk-1 ) ■■=KF(fˆ k(-k1-|k2-)1,Pk f-1(|kk--21),Fk,Hk,Rˆ k-1,zk)后向平滑：For j =k: (-1):(k-L+1)2.■■fˆ j(-k1-|k1),Pj f-1(| kk-1 ) ■■=KS(fˆ j(| kk-1 ),Pj|fk(k-1 ),fˆ j(-j1-| j2-)1,Pj f-1(|jj--12))3.计算Bj End for 4.使用公式（35）计算Bk-L在线估计 Rk ：5.使用公式（28）计算uˆ k| k-1 和Uˆk| k-1 6.使用公式（33）计算uˆ k|k和Uˆk|k 7.使用公式（37）计算Rˆk输出：{ fˆ j(| jj-1 ),Pj|f j( j-1 )|k-L+1≤j ≤k},uˆ k|k,Uˆ k|k,Rˆk

4 仿真验证

为了验证本文提出算法的有效性，首先完成惯性导航系统和卫星系统的导航解算。在此基础上，给模拟的卫星数据加均值为零以及特定方差大小的高斯白噪声，产生1 套带有随机误差的传感器数据，并在仿真数据中添加一定大小的阶跃故障或缓变故障信号，分别用本文方法和模拟的真实故障信号做仿真，验证故障估计效果及故障补偿的效果。导航系选取东北天坐标系，飞行器飞行轨迹如图1所示。

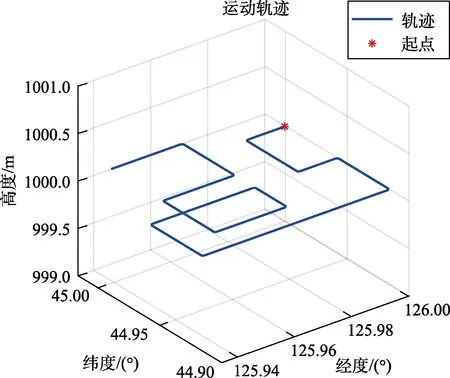
图1 飞行轨迹Fig.1 Flight trajectory

设置飞行总时长为2860 s。常规情况下传感器的参数如表1所示。

表1 仿真参数设置Table 1 Simulation parameter settings

同时，设置阶跃故障和缓变故障模型数学模型分别为Fs(Int_t,D,Size)与Fs1(Int_t,D,Ratio)。其中，Fs 表示的是阶跃故障模型，Fs1 表示的是缓变故障模型，Int_t为故障开始时间，D为故障持续时间，Size 表示的是故障的大小，Ratio 为故障变化率。

4.1 故障方案

仿真中假设卫星导航系统存在突变故障或者是缓慢变化故障，具体故障状况如表2所示。进一步可得故障下的卫星导航系统经纬度量测值误差曲线，如图2～5 所示。

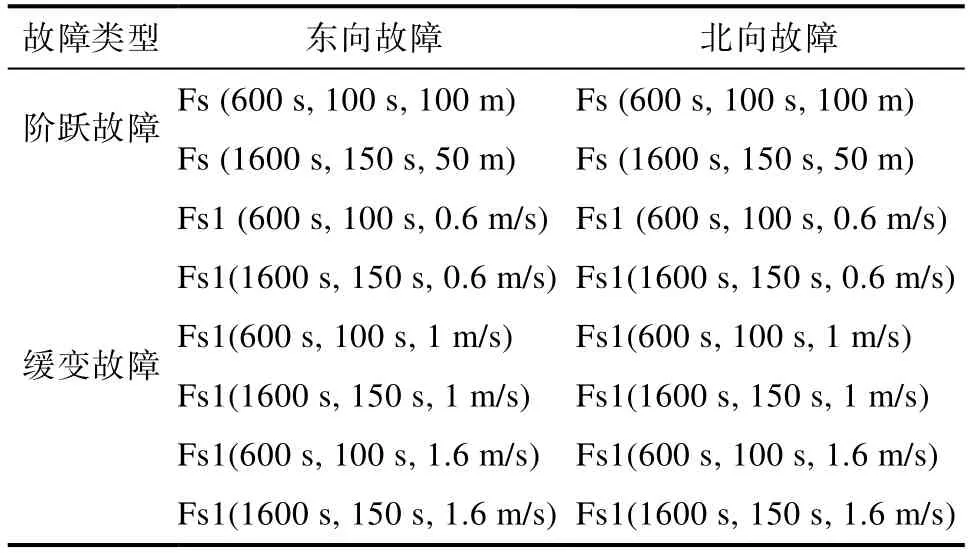
表2 故障方案Table 2 Fault solutions

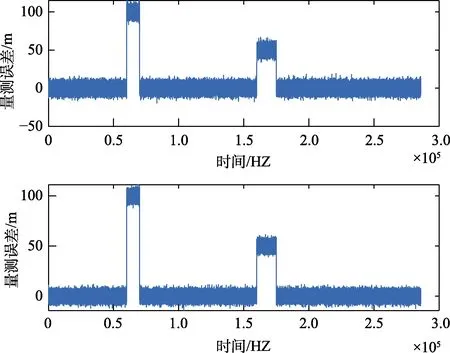
图2 阶跃故障经纬度量测误差曲线图Fig.2 Step fault longitude and latitude measurement error curve

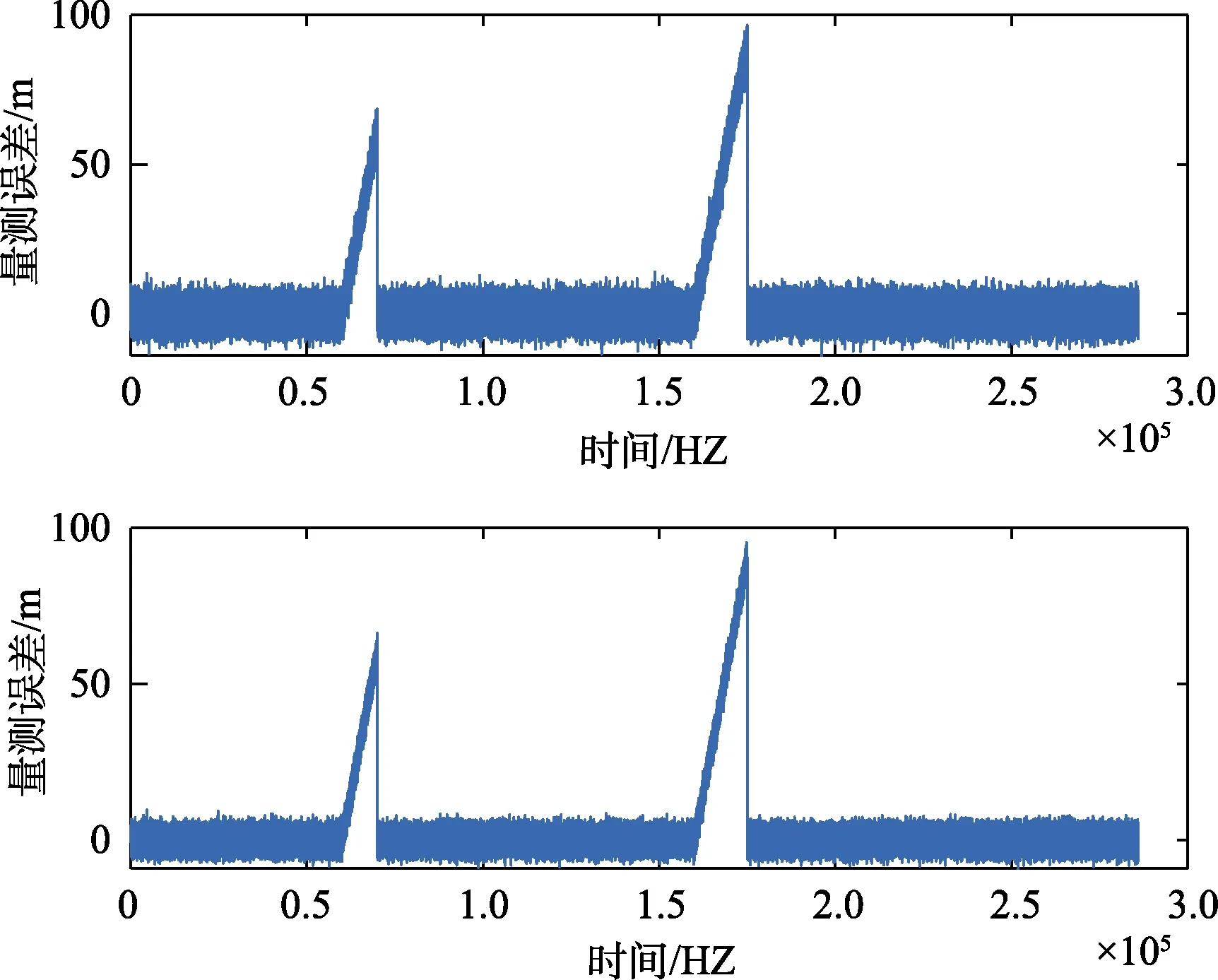
图3 缓变故障经纬度量测误差曲线图1Fig.3 Slow fault longitude and latitude measurement error curve 1

为验证滑窗变分自适应算法在故障估计及补偿中的性能，在表2所示的卫星导航系统故障下，对比了模拟的真实故障信息，VB 估计故障及补偿以及本文提出的算法对SINS/GPS 组合导航系统进行GPS 故障估计及补偿的差异。三种方法的结果如下所示。

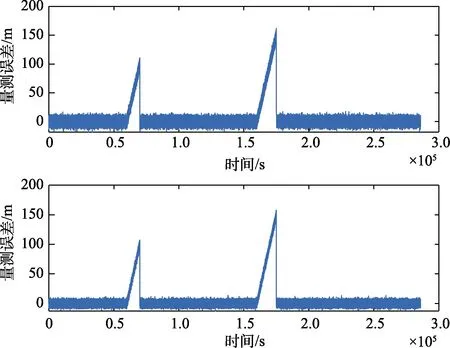
图4 缓变故障经纬度量测误差曲线图2Fig.4 Slow fault longitude and latitude measurement error curve 2

4.2 阶跃故障

通过对GPS 添加不同大小的突变故障信号，来验证本文所提出的方法。首先，在600～700 s内给GPS 注入幅值为100 m 的故障信号；然后，在1600～1750 s 内给GPS 注入幅值为50 m 的故障信号，得到的仿真结果如图6所示。其中，红色线表示模拟的真实故障信号，蓝色线表示本文算法所估计出来的故障信号，绿色线表示利用变分算法估计出来的故障值。从图6以及表3可以看出，在故障开始时本文所提出的算法和VB 都可以在故障开始时很好地估计出来故障值的大小，但是本文提出的算法与模拟的故障信号二者之间的差值小于VB 算法估计出来的故障值与模拟的真实故障值两者之间的差值。因此，本文所提出的算法对突变故障有更好的估计精度。

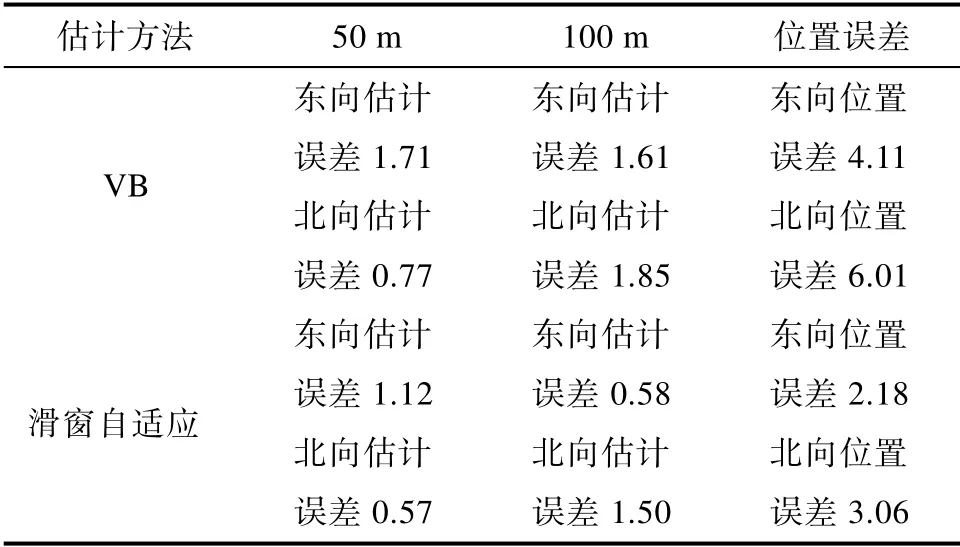
表3 不同突变故障估计值误差Table 3 Error translation of different mutation fault estimates

在估计出故障信号的基础上，我们对不同时刻不同大小的突变故障进行了补偿，补偿后的结果如图7所示，图7表示的是在600～700 s 以及1600～1750 s 这两段时间内分别对添加的100 m和50 m 故障进行补偿后的误差。其中，红色线表示未进行故障补偿的误差，蓝色线表示采用本文提出的方法进行误差补偿的结果，绿色线表示VB 对故障信号进行补偿之后的位置误差。从图中我们可以看出来，在600 s 以及1600 s 时，真实的误差图有明显的偏置，这是因为此时GPS 已经有了故障。但是由于在 600～700 s 以及在1600～1750 s 期间，我们提出的算法以及VB 算法在估计出故障信号后对故障信号进行了补偿。因此蓝色和绿色的误差结果有明显的减小，并且本文提出的算法得到的误差明显小于利用VB 算法得到的误差。

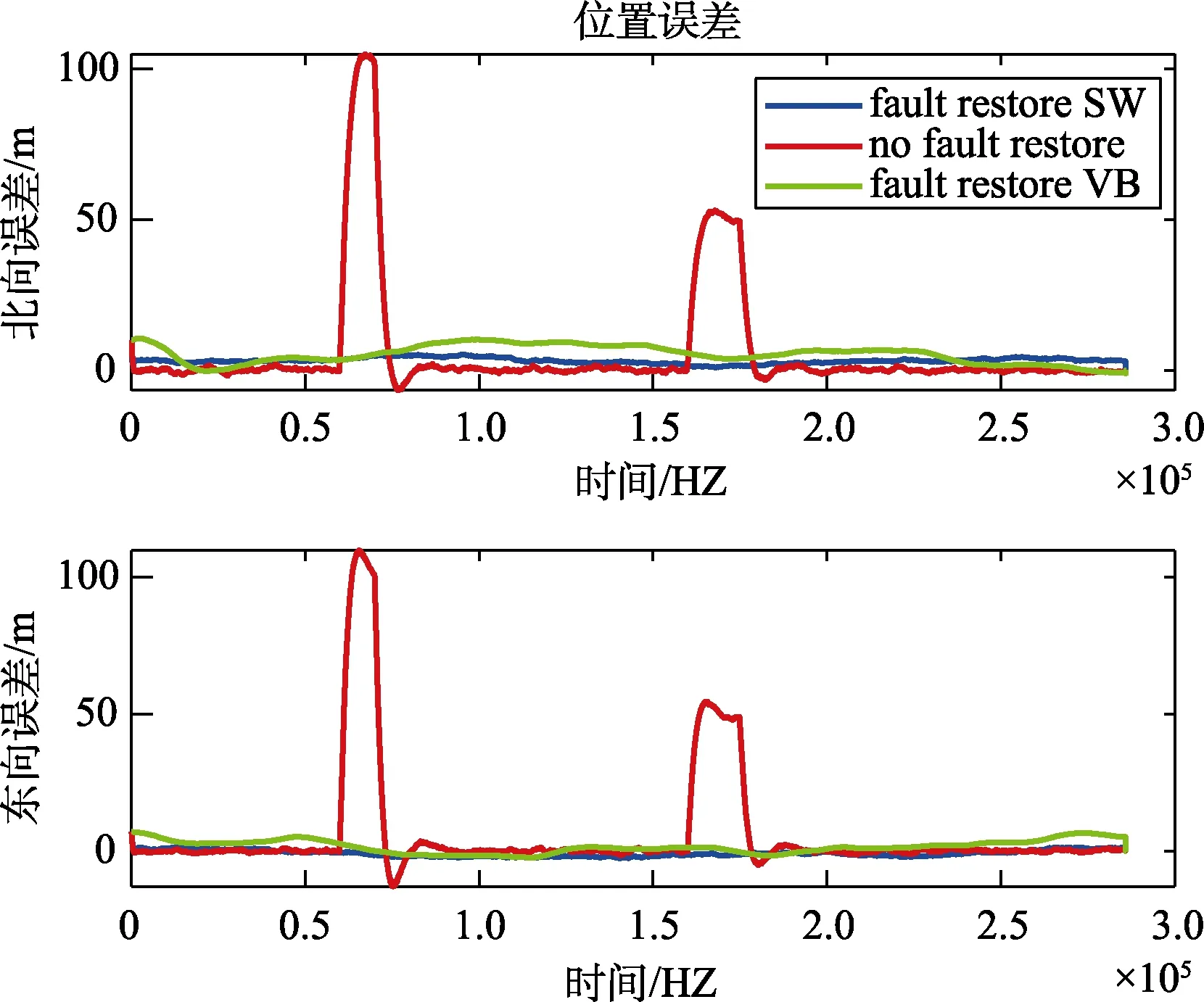
图7 阶跃故障修复误差图Fig.7 Step fault repair error diagram

4.3 缓变故障

首先，为了更好地验证滑窗变分自适应算法在故障估计与补偿中的性能，在600～700 s 内给GPS 添加了不易检测出来的缓变故障信号，故障变化率分别为0.6 m/s、1 m/s 和1.6 m/s；其次，为了凸显本文所提出的算法对不同时长的故障信号仍具有很好的估计及补偿效果，在1600～1750 s内分别给GPS 添加了不易检测出来的缓变故障信号，故障变化率分别为0.6 m/s、1 m/s 和1.6 m/s，得到的仿真结果分别如图8～10 所示。其中，红色线表示模拟的真实故障信号，蓝色线表示本文算法所估计出来的故障信号，绿色线表示利用变分算法估计出来的故障值。从图8～10 以及表4可以看出，在缓变故障刚开始时故障值非常小，本文所提出的算法和VB 都可以很好地在故障刚开始时就估计出来故障值的大小，但是本文提出的算法与模拟的故障信号二者之间的差值小于VB 算法估计出来的故障值与模拟的真实故障值两者之间的差值，因此本文所提出的算法对缓变故障有更好的估计精度。

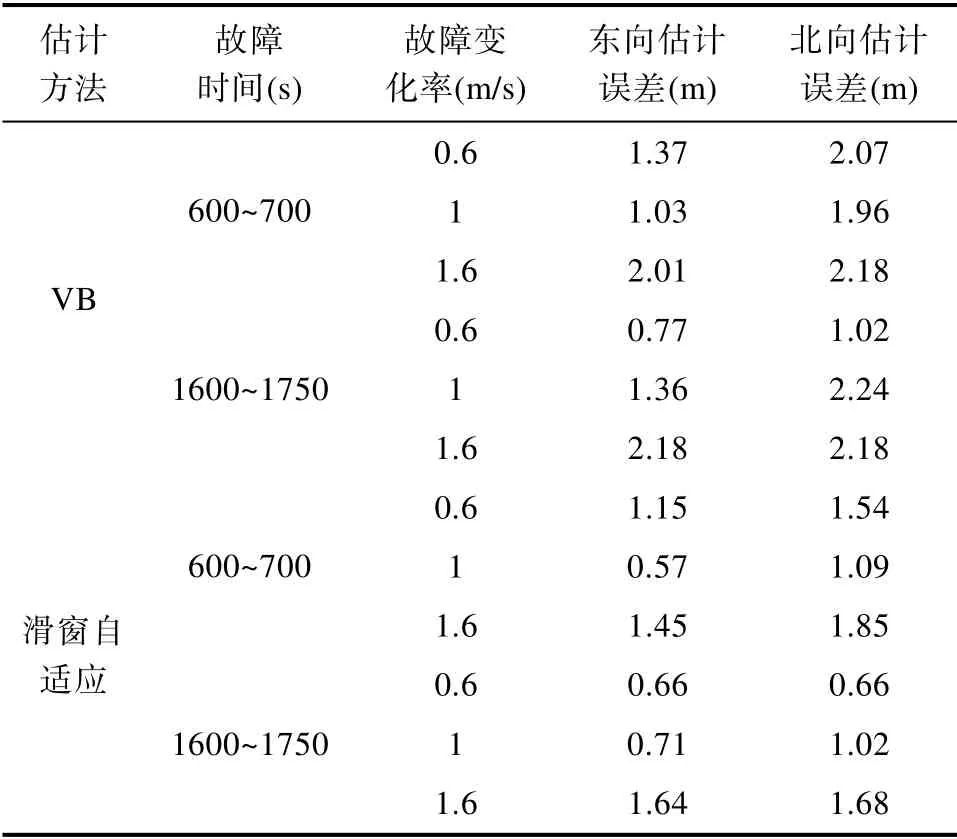
表4 不同缓变故障估计值误差Table 4 Error translation of different slow-varying faultestimates

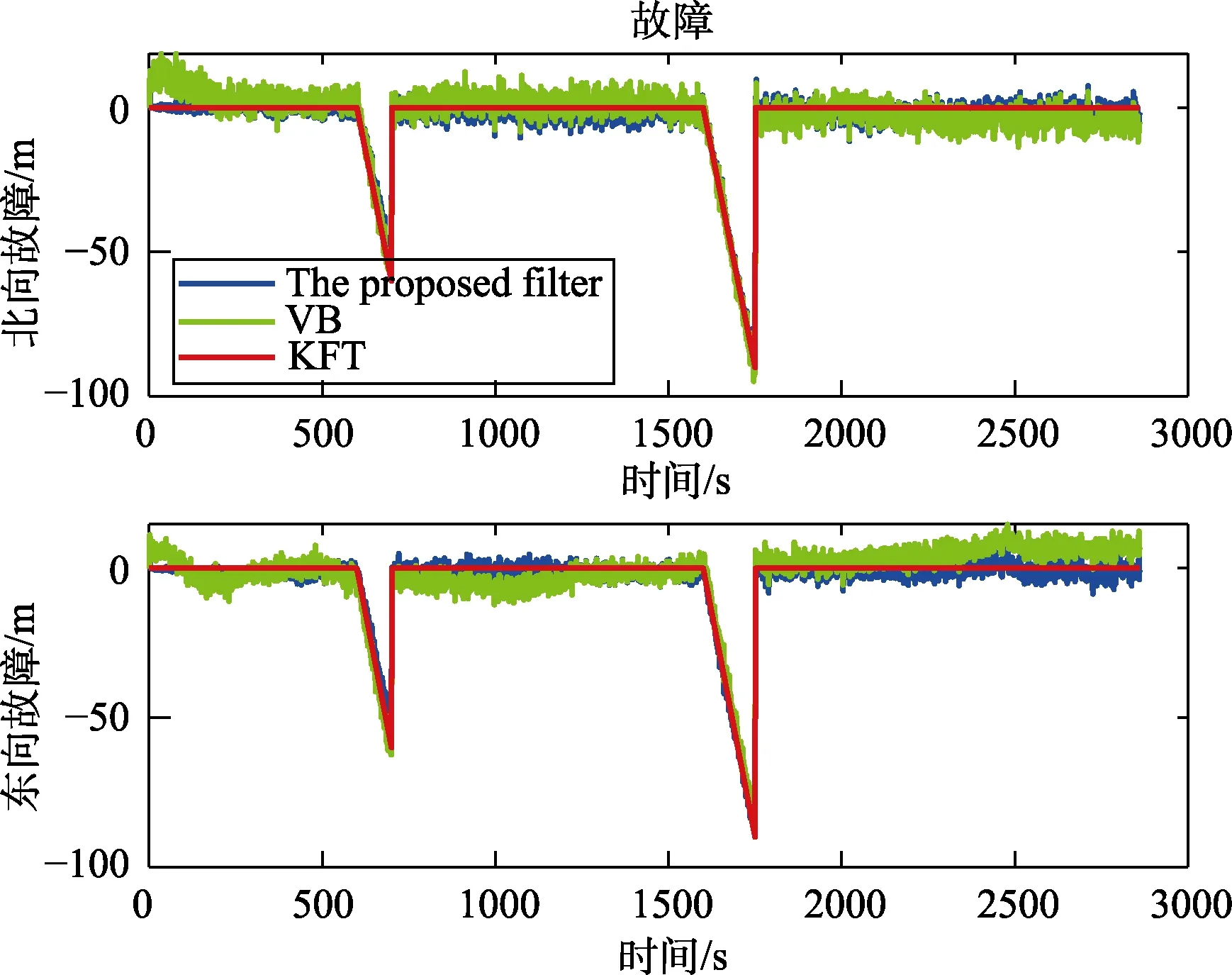
图8 斜坡故障估计图1Fig.8 Slope fault estimation diagram 1

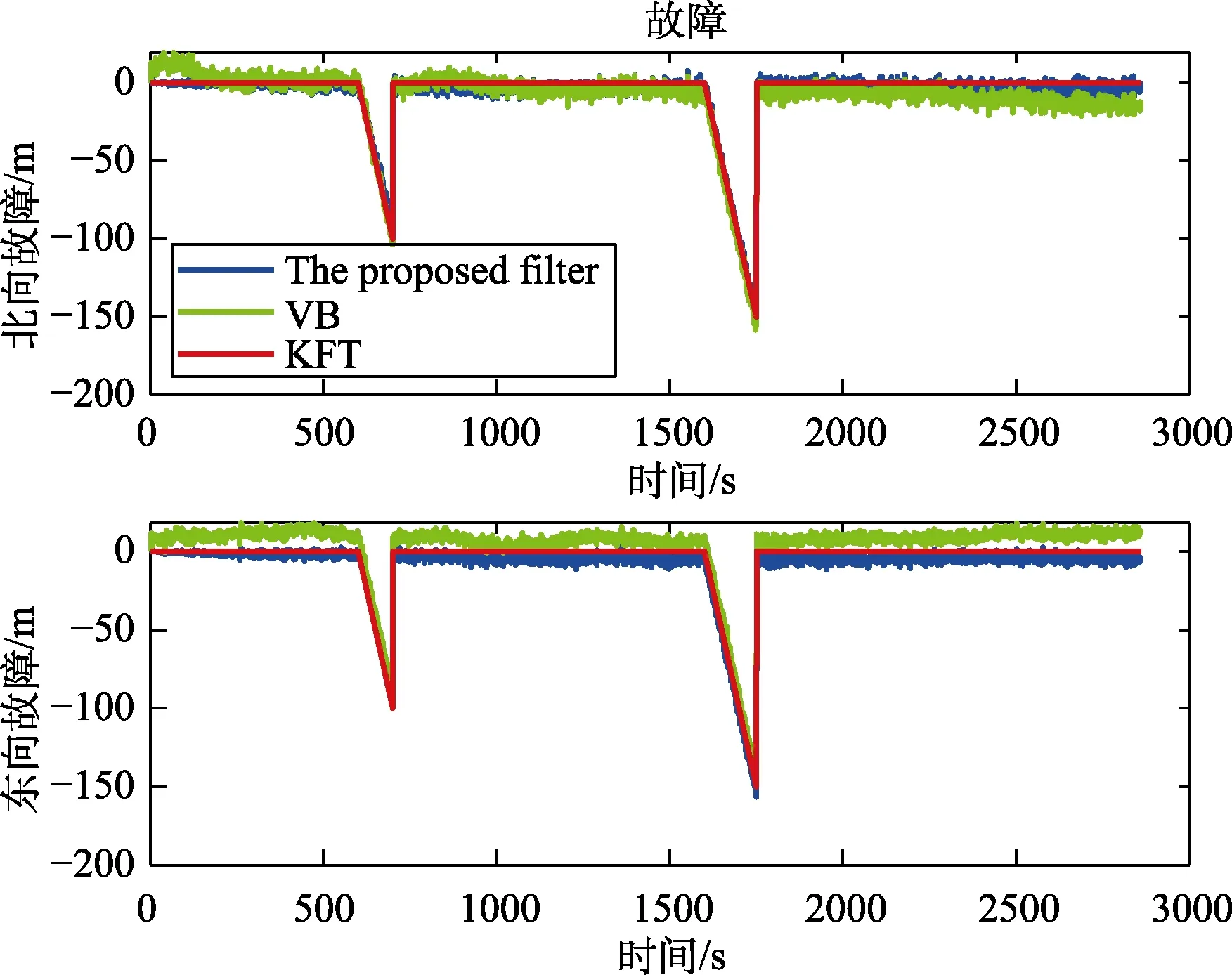
图9 斜坡故障估计图2Fig.9 Slope fault estimation diagram 2

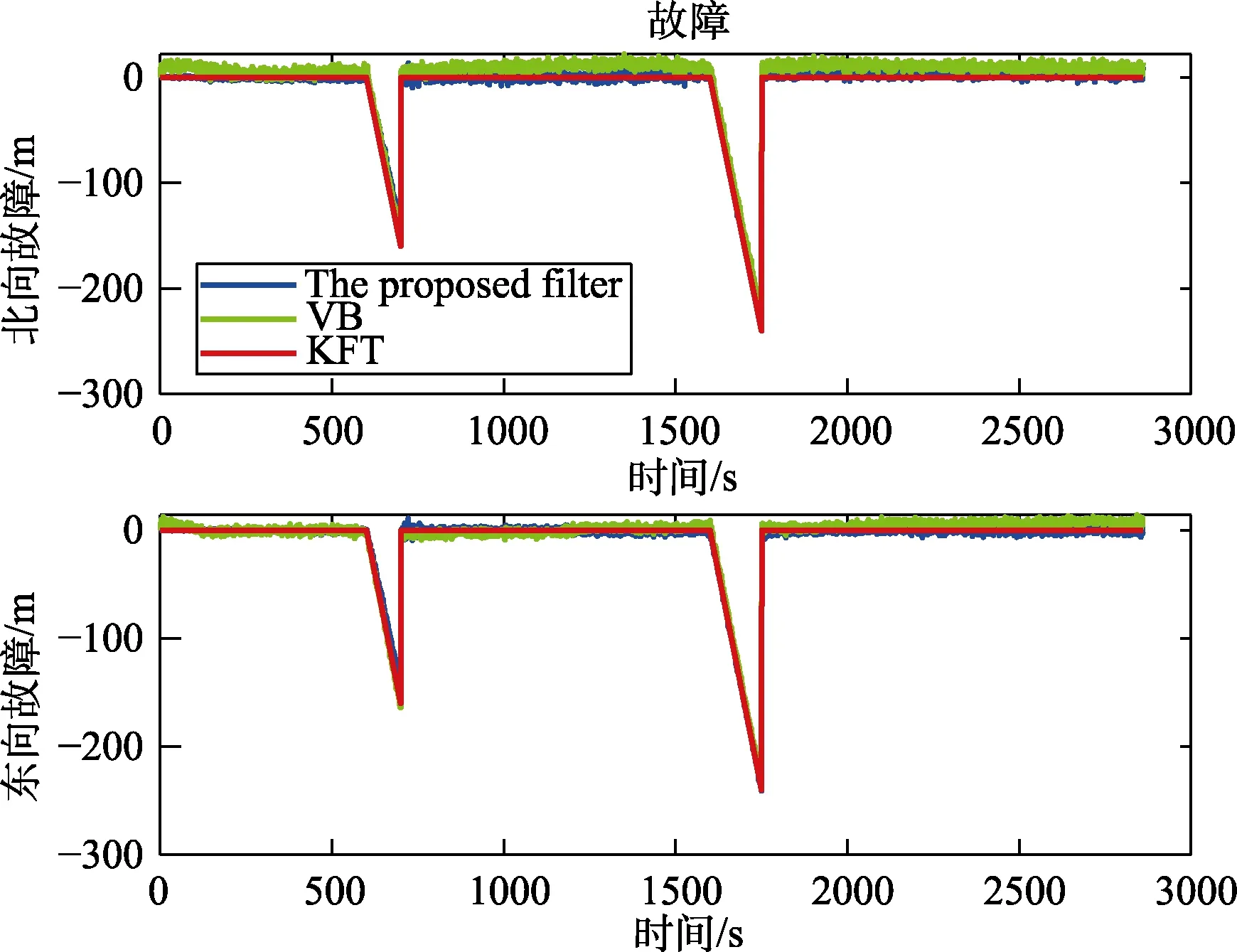
图10 斜坡故障估计图3Fig.10 Slope fault estimation diagram 3

在估计出故障信号的基础上，我们对不同时刻不同变化率的缓变故障信号进行了补偿，补偿后的结果分别如图11～13 所示。图11表示在600～700 s 以及1600～1750 s 这两段时间内的故障变化率为0.6 m/s 的故障进行补偿后的误差。图12表示在600～700 s 以及1600～750 s 这两段时间内的故障变化率为1 m/s 的故障进行补偿后的误差。图13表示在600～700 s 以及1600～1750 s 这两段时间内的故障变化率为1.6 m/s 的故障进行补偿后的误差。其中，红色线表示未进行故障补偿的结果，蓝色线表示采用本文提出的方法进行误差补偿的结果，绿色线表示VB 对故障信号进行补偿之后的结果。从图中可以看出来，在600 s以及1600 s 时，真实的位置误差有较小的偏置，这是因为此时GPS 已经有了故障。但是由于在600～700 s 以及1600～1750 s 这两段时间内，我们提出的算法以及VB 算法在估计出故障信号后对故障进行了补偿，所以蓝色和绿色的误差结果有明显的减小。从表5可以看出来，本文提出的算法得到的位置误差明显小于利用VB 算法得到的位置误差。因此，本文所提出的滑窗变分自适应算法不仅对不同类型故障信号有很好的估计效果，而且提高了有故障情况下导航的精度。

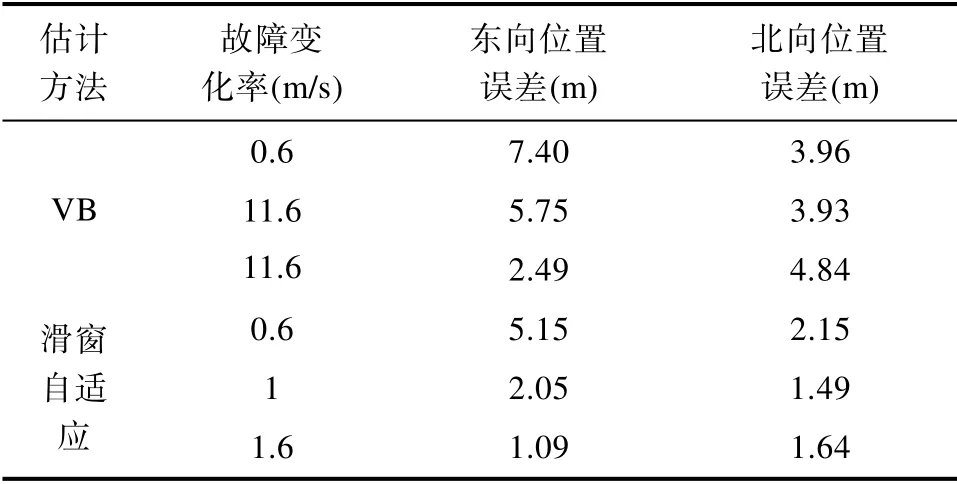
表5 不同缓变故障位置误差Table 5 Error translation of different slow-varying position error

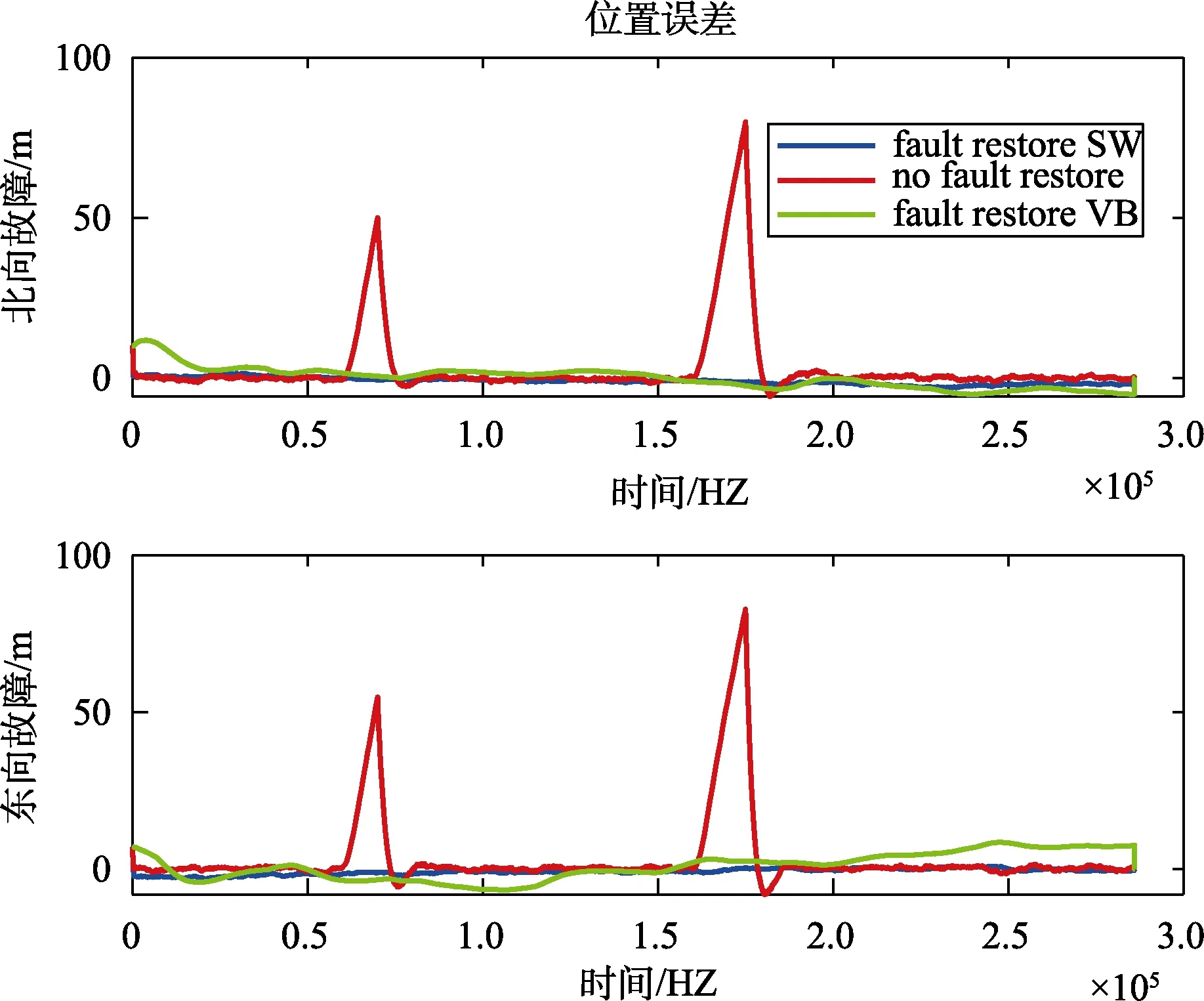
图11 斜坡故障修复误差图1Fig.11 Slope fault repair error diagram 1

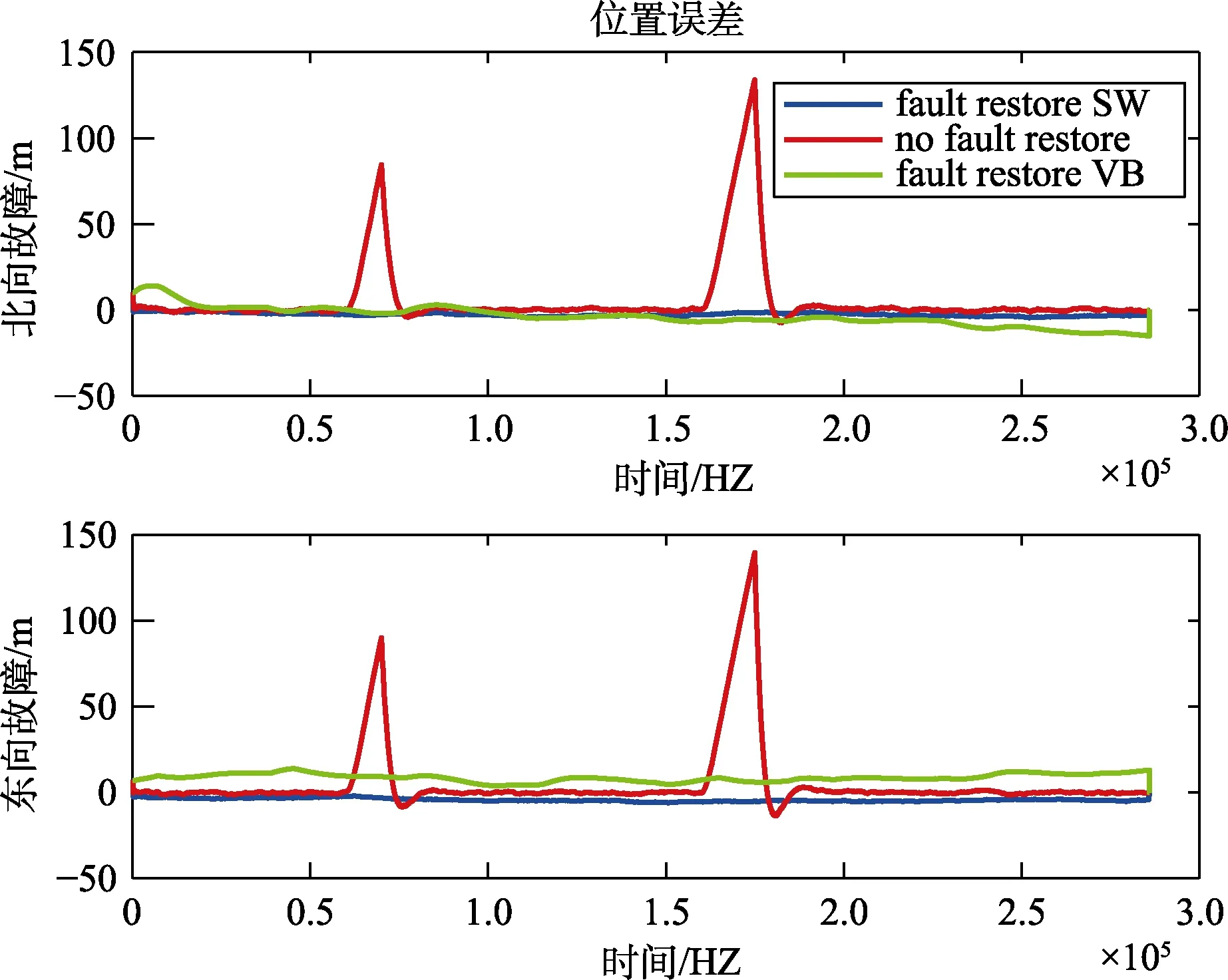
图12 斜坡故障修复误差图2Fig.12 Slope fault repair error diagram 2

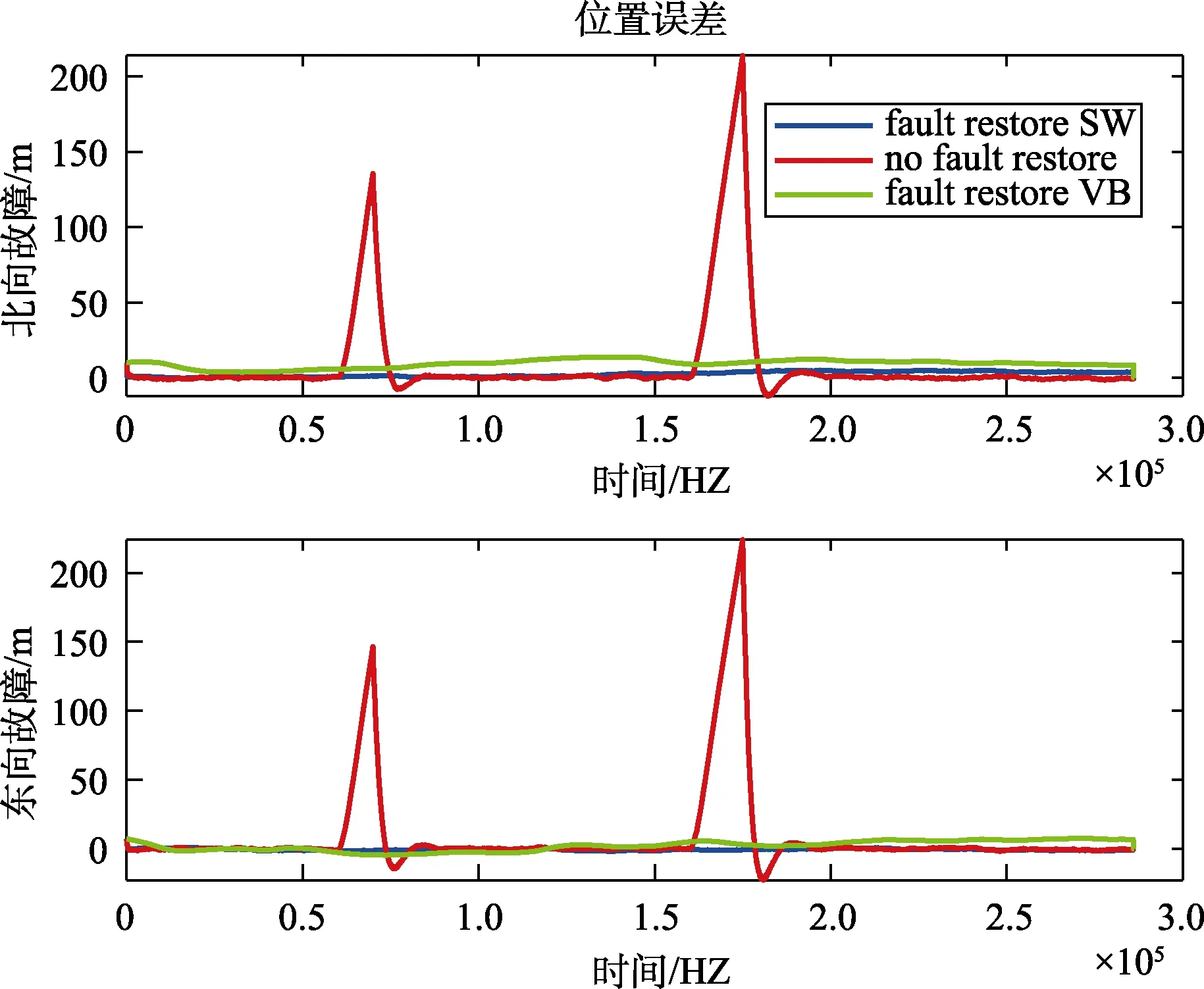
图13 斜坡故障修复误差图3Fig.13 Slope fault repair error diagram 3

5 结 论

本文主要围绕实现一种故障估计及修复方法以及提高导航系统可靠性的内容展开研究工作。首先介绍并分析了传统方法的缺陷。然后，提出了一种新的滤波器来估计未知测量噪声协方差和未知故障的传感器故障系数矩阵。具体来说，利用滑窗变分自适应滤波算法对传感器故障信号和量测噪声进行了同时估计。最后，基于SINS/GPS组合导航系统，通过仿真，对滑窗变分自适应滤波算法的故障估计及补偿能力进行了评估。仿真结果表明，与真实的故障信号相比，该方法具有很好的估计精度，且采用了该算法的SINS/GPS的组合导航系统也显示出了更好的可靠性，证明了该算法对故障具有较好的估计及补偿能力。