适用于水下高速机动目标的自适应检测方法

孙苇轩，闫 晟，郝程鹏

（1.中国科学院声学研究所,北京 100190；2.中国科学院大学电子电气与通信工程学院,北京 100049）

1 引 言

近几十年来，随着人们对海洋资源的开发及安全维护，大力发展水下目标检测技术逐步成为水声领域的研究重点[1-3]。水下目标检测技术可分为主动声呐和被动声呐检测技术。对于主动声呐检测，混响是干扰主动声呐检测性能的主要因素之一[4]。从统计信号处理角度出发，提出一种主动声呐检测技术的重要类型：水下目标自适应检测技术，简易流程图如图1所示。由图中可以看到，其核心为检测方法设计，该部分工作基于辅助数据和待检测数据即可完成，在检测方法设计过程中可通过干扰协方差矩阵白化以达到混响抑制目的，同时获得自适应检测统计量，而后通过预设虚警概率（Probability of False Alarm,Pfa）求得检测阈值，经过检测判决实现最终的目标检测。该方法通过检测阈值的自适应调整使Pfa保持稳定，不受背景干扰影响，从而能够保证CFAR性能[5-6]。

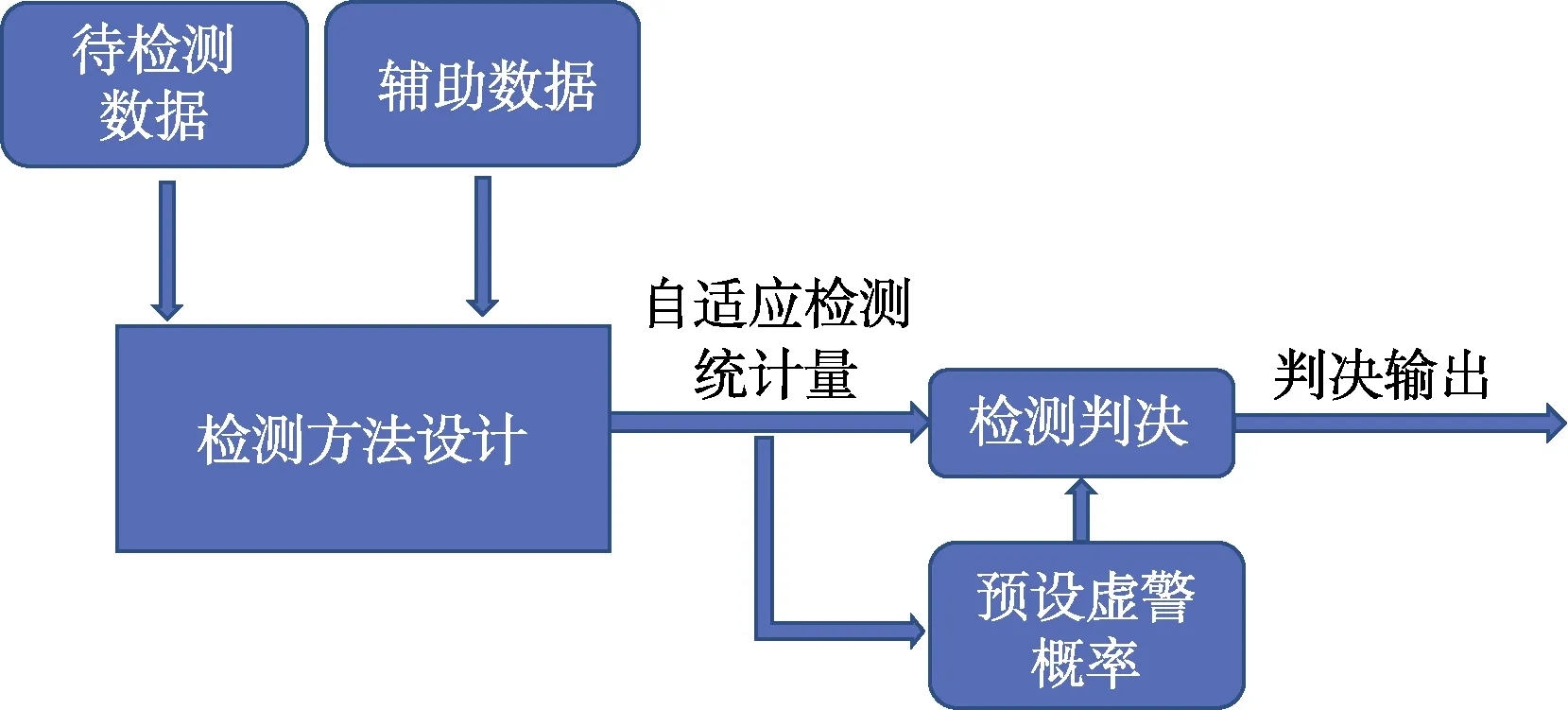
图1 水下目标自适应检测示意图Fig.1 Underwater target adaptive detection schematic

浅海探测环境中，水下目标自适应检测技术在实际应用时会面临一些问题。例如，浅海环境复杂多变[7-8]，常常为非平稳非均匀等不理想的环境，导致辅助数据难以获取，想要达到RMB 准则[9]中两倍以上系统维度的辅助数据量非常困难。为了解决这一问题，国内外学者们利用先验知识来降低自适应检测方法对辅助数据的依赖性，包括采用干扰协方差的斜对称特性、背景干扰功率谱对称性或者结合贝叶斯思想等[10-17]，提出了一系列可以有效降低辅助数据量的自适应检测方法，如：均匀环境下的斜对称修正GLRT、均匀环境下的斜对称修正AMF 等检测方法。

另一个需要重点关注的问题是目标高速运动导致的RCM 现象。简单来说，就是目标在高速运动的情况下，可能在主动声呐发射信号结束前已经离开观测区域，导致一个距离单元内不全部包含目标回波，如图2所示。图中，浅蓝色色块代表包含目标回波的采样点。此时，高速机动目标回波分布可能会有图中4 种情况。该现象导致目标回波能量不能有效积累，从而引起目标检测性能下降[18]。针对这一问题，在雷达领域中，已有Hough 变换[19-20]和Keystone 变换[21-22]相关算法能够补偿RCM 现象。其中，Hough 变换将接收数据进行脉冲压缩后构造霍夫变换矩阵，重新累加转移到其他距离单元的目标回波能量，实现RCM 现象的补偿。而Keystone 变换通过数据坐标系的尺度变换来补偿RCM 现象，从而减少目标高速运动导致的能量损失。这两种补偿RCM现象的方法皆存在脉冲压缩步骤，而声呐采用单脉冲工作形式[23]，不存在该步骤，因此Hough 变换和Keystone 变换在水下目标自适应检测中不再适用。针对这一问题，文献[24]改进水下空时模型[25]，建立水下高速机动目标的多元假设检验模型，结合MOS 方法，无需考虑目标运动的先验信息，提出一种斜对称广义信息准则自适应匹配滤波（Persymmetric Generalized Information Criterion Adaptive Matched Filter,PG-AMF）方法。该方法提高了对目标回波的能量积累，提高目标检测性能。但该方法仅使用待检测数据估计未知参数，未能联合使用待检测数据和辅助数据，降低了所得未知参数MLE 的准确度，回波数据不能被有效利用，影响了目标检测性能。

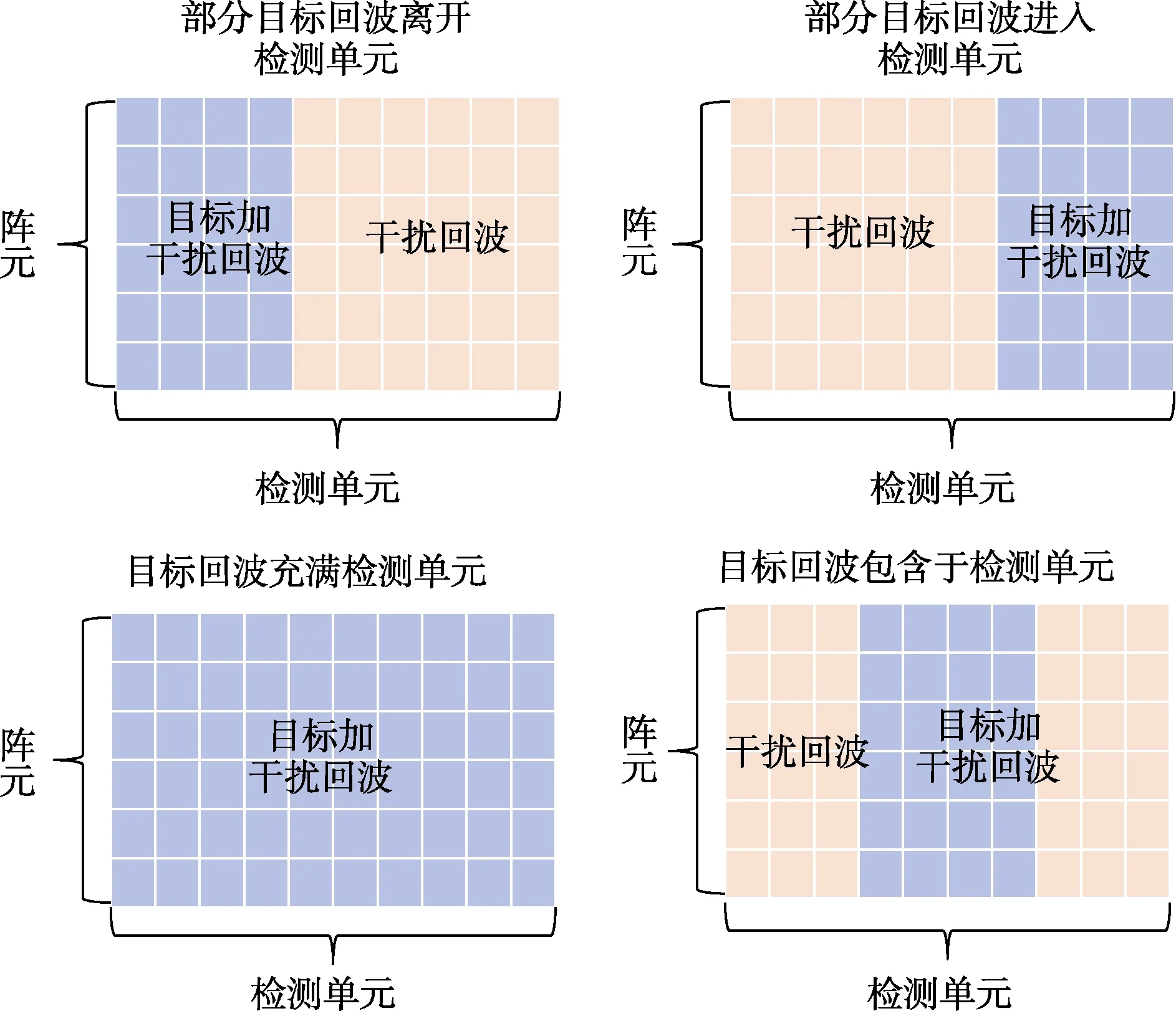
图2 高速机动目标回波分布Fig.2 High-speed maneuvering target echo distribution

针对上述问题，本文基于GLRT 准则提出一种适用于水下高速机动目标的斜对称广义信息准则一步GLRT（Persymmetric Generalized Information Criterion One Step GLRT,PGOS-GLRT）检测方法。首先引用文献[24]的水下高速机动目标多元假设检验模型，将目标回波位置准确表示，利用MOS 方法[26]中的广义信息准则（Generalized Information Criterion,GIC）实现对目标回波位置的估计，并结合背景干扰协方差的斜对称特性，减少检测方法对辅助数据的需求量。接下来基于一步GLRT 准则，联合使用待检测数据和辅助数据来实现未知参数的 MLE，相比于已有的PG-AMF 检测方法中仅使用待检测数据的次优估计，大大提高了回波数据的利用率，最后将求得的各个未知参数的MLE 代入GLRT 检测统计量中，得到最终的PGOS-GLRT 检测方法。仿真结果表明，所提检测方法的Pfa保持稳定，不受背景干扰的影响，具有CFAR 特性。此外，PGOS-GLRT检测方法相比于其他同类检测方法性能得到显著提升，有着较为明显的目标检测性能优势，同时对目标回波分布情况估计的精确度更高。

2 系统模型

2.1 接收信号模型

首先对接收回波的信号模型进行介绍。对于高速机动目标，其回波分布参考水下空时模型，在一个探测周期发射信号脉宽为PT，接收阵元接收连续回波后进行连续时间采样，以PT长度为单位将采样数据分为若干距离单元，忽略时域相关性，将每个采样点数据分开表示，如图3所示。

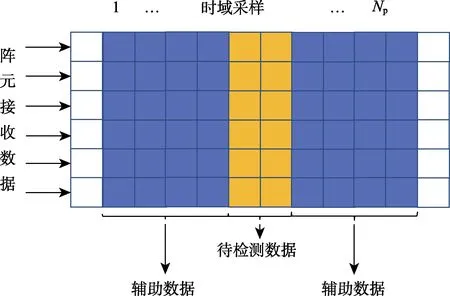
图3 接收数据采样Fig.3 Received data sampling

假设使用一个阵元数为N，阵元间距为d的均匀线阵对目标回波进行接收，取阵元间距为d=λ/2，其中λ为发射信号波长，各个阵元之间的增益均等、互耦不计。对接收回波信号进行一系列信号处理之后，假设采样频率为fs，发射脉冲信号为

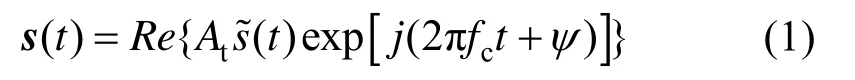
式中，Re{ }· 表示取实部信号，tA表示幅值因子，s～(t) 为矩形脉冲包络，fc为载波频率，ψ为系统初始相位。

则第n个阵元接收到的目标回波的第m个采样点可表示为

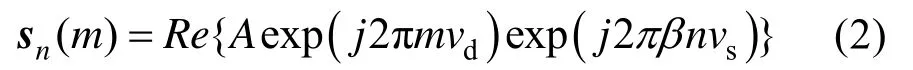
式中，A为包含信号幅度的系数；vd=fd/fs为时域频率；vs=dsinδ/λ为空域频率；δ为目标方位角；fd=(2v/c)fc为信号多普勒频率，其中v为平台与目标相对径向速度，c=1500 m/s为水下声速；β=1+2v/c为信号拉伸或压缩系数。

2.2 假设检验构建

为解决RCM 现象导致的检测性能下降问题，本文采用文献[20]的多元假设检验模型，引入参数l,h准确描述采样点包含的目标回波位置，如式(3)所示，定义采样点幅值为α=Aexp(j2πmvd)。

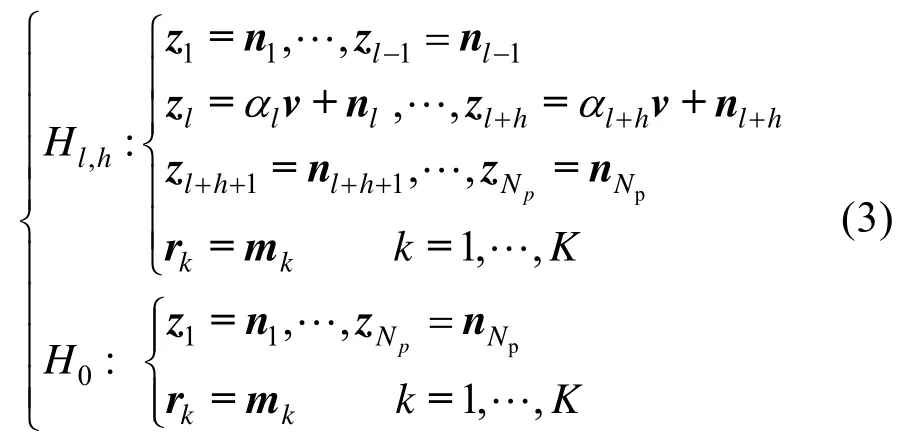
式中，R=[r1…rK]为辅助数据，Z=[z1…zNp]为待检测数据，且有R∈CN×K，Z∈CN×Np，其中K表示辅助数据个数，Np表示待检测单元内的采样点个数。同时，为保证干扰协方差矩阵的非奇异性，需满足K≥N；ni,mk～CNN（0,M）为独立同分布的背景干扰，服从零均值多元复高斯分布，干扰协方差矩阵表示为M；l,…,l+h表示包含目标回波的采样点，有1≤l≤Np，0≤h≤Np-1，且l+h≤Np，αi表示第i个采样点的幅度，i=l,···,l+h；v为导向矢量：

为了有效降低检测方法对辅助数据的依赖性，这里采用干扰协方差矩阵的斜对称特性，即满足M=J NM *JN，v=J Nv*。其中，(·)*表示共轭运算。JN如式(5)所示为N维置换矩阵。

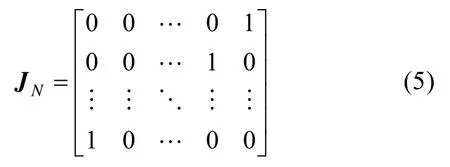
此时，可以将适用于高速机动目标的多元假设检验问题改写为

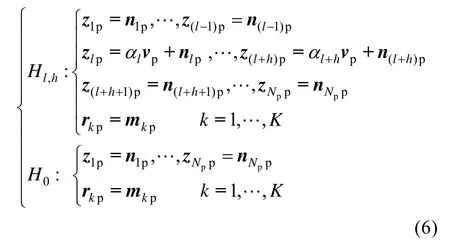
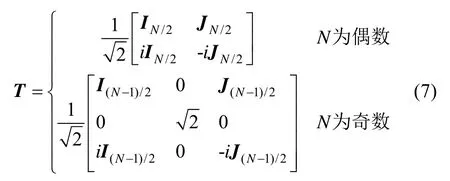
式中，IN表示阶数为N的单位矩阵。

3 检测方法设计

为求解式(6)中的假设检验问题，下面采用一步GLRT 准则设计高速机动目标模型下的自适应检测方法PGOS-GLRT。PG-AMF 方法单独使用待检测数据估计未知参数，得到的参数估计精度有限，限制了该方法的检测性能。为进一步提升辅助数据数量受限情况下的目标检测性能，本文首先联合待检测数据和辅助数据实现检测统计量的推导和未知参数MP和α的MLE，然后结合MOS 方法对l，h的值进行估计，估计值记为、，以获得更高的检测性能。

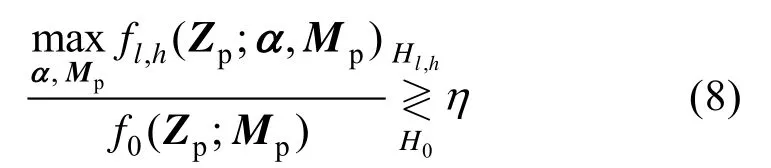
式中，η表示一定Pfa下的检测阈值，f l,h(Zp;α,Mp)表示在Hl,h假设下联合数据矩阵Zp=[Z IpZKp]的概率密度函数（probability density function，PDF），f0(Zp;Mp)表示在H0假设下联合数据矩阵Zp=[Z IpRKp]的PDF，表达式分别为

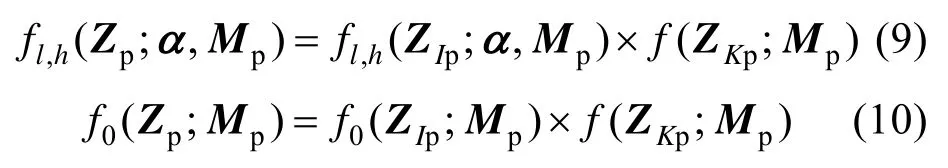
式中，f l,h(ZIp;α,Mp)和f0(Z Ip;Mp)分别表示在Hl,h和H0假设下待检测数据ZIp的 PDF，f(RKp;Mp)表示辅助数据的 PDF，其表达式分别为

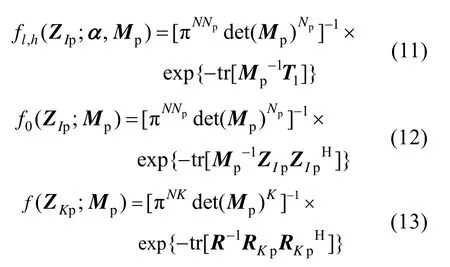
式中，det(·) 表示行列式运算，tr[·]表示求迹运算，(·)-1表示求逆运算，(·)H表示共轭转置运算，且有

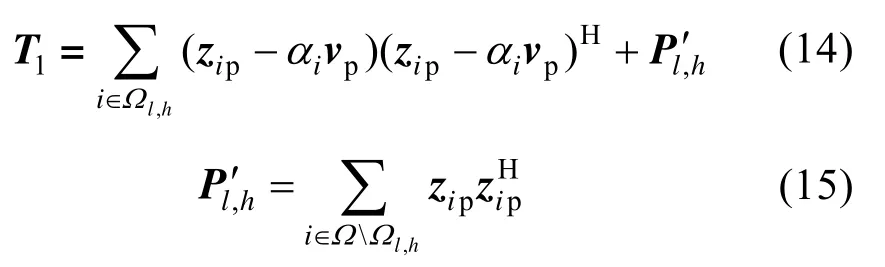
式中，Ωl,h={l,…,l+h}，ΩΩl,h为Ωl,h对Ω的补集。

将式(11)、(13)及(14)代入式(9)，式(12)和(13)代入式(10)中，分别得到

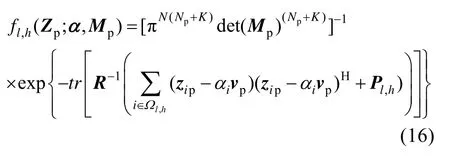
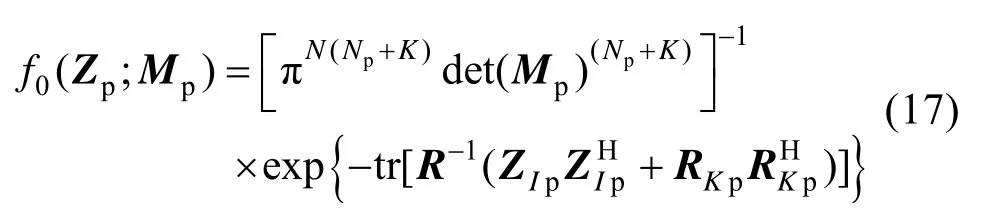
使用MLE 方法对Hl,h、H0假设下的Mp进行估计：

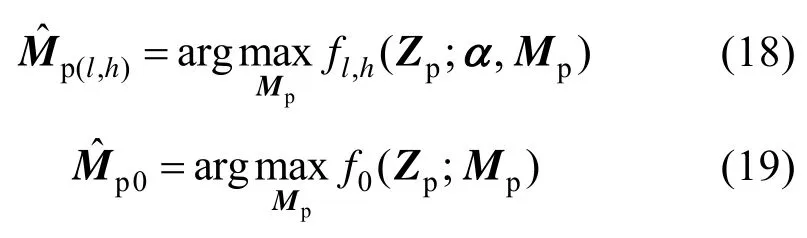
对 PDF 取对数后，分别求对数函数ln[f l,h(Zp;α,Mp)]和 ln[f0(Zp;Mp)]关于Mp的导数并置0，得到如下估计结果

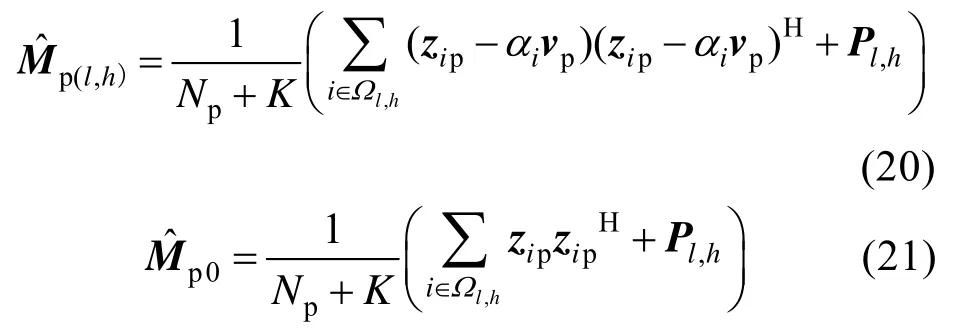
将式(16)、(17)、(20)、(21)代入式(8)，则检测表达式可重新整理为

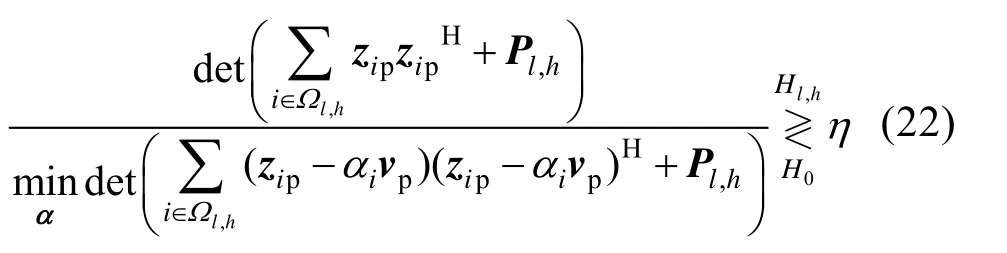
在Hl,h假设条件下，计算α的估计值，基于式(22)，对α的MIL 等价于

得到估计结果为

将式(24)代入(22)中，检测表达式等价于

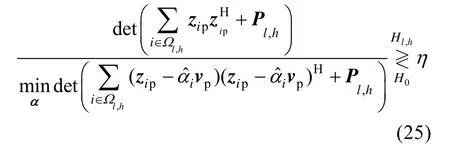
接下来，使用MOS 方法对目标回波位置进行估计，由文献[24]可知，在各类准则中，GIC准则表现最优。因此，本文采用GIC 准则进行对l、h的估计，对应的模型维度为q=2(h+1)+N2，则对l、h进行估计的表达式为

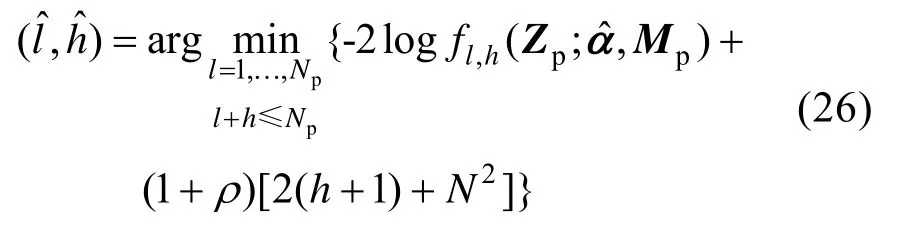
式中，ρ＞1表示经验常数，需根据实际应用情况进行合理设置[24]。将各个参数的估计值代入式(26)，得到、的表达式为

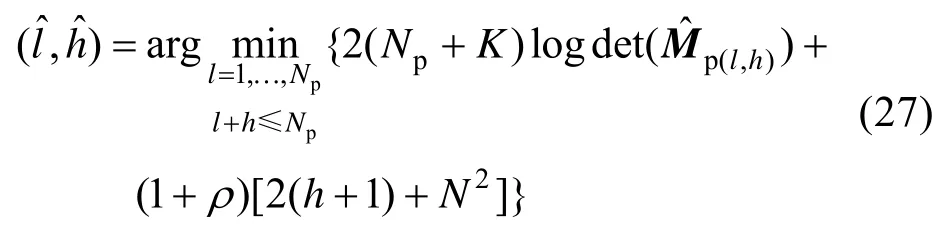
最后，利用、，将式(27)代入式(25)，得到PGOS-GLRT 检测方法最终表达式为

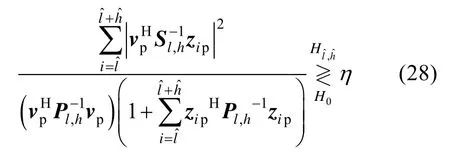
4 仿真结果及分析

接下来采用蒙特卡洛仿真实验对所提PGOS-GLRT 检测方法的CFAR 特性以及目标检测性能进行仿真分析。假设系统采用半波长等间距的均匀线阵，阵元数Nα=10，采样点个数Np=20，目标方位角δ=0°，GIC 准则参数为ρ=5，干扰协方差矩阵建模为M=IN+pcMc，其中IN为N维单位矩阵，pc为混响功率，Mc(i,j)=为基于指数相关复高斯模型的混响差矩阵，ρc为一步滞后相关系数。l、h值分别均匀分布于[0,Np-1]和[1,Np-l]。最后，为观测算法的检测性能，定义信混噪比(Signal to Reverberation plus Noise Ratio,SRNR)SRNR=,混 响 噪 声 比(Reverberation to Noise Ratio,RNR)RNR=pc/σN2。

4.1 C FAR 特性

首先验证PGOS-GLRT 检测方法的CFAR 特性，预设Pfa=10-4，蒙特卡洛仿真次数L=100/Pfa，取SRNR=25 dB，K=20,ρc=0.9。

图4给出了PGOS-GLRT 检测方法的Pfa随RNR 的变化曲线，可以看到，RNR 从10 dB 变化至20 dB，Pfa一直稳定在 10-4左右，不受背景干扰影响，即所提检测方法关于RNR 是CFAR 的。

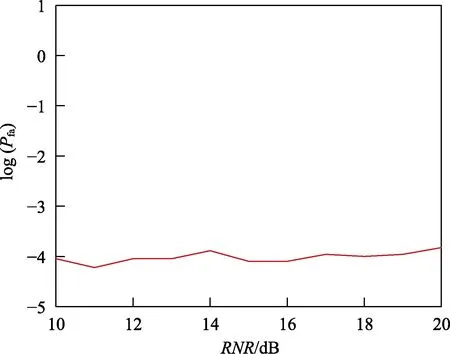
图4 PGOS-GLRT 的Pfa 随RNR 的变化曲线Fig.4 Pfa versus RNR for the PGOS-GLRT

接下来观测PGOS-GLRT 检测方法的Pfa随混响随协方差矩阵Mc中参数ρc的变化曲线，保持其他参数不变，设RNR=20 dB。由图5表明，当ρc从0.5 增大至1 时，PGOS-GLRT 检测方法的Pfa始终稳定在 10-4左右，即所提检测方法关于ρc是CFAR 的。

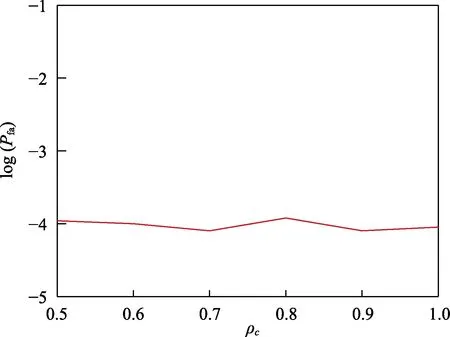
图5 PGOS-GLRT 的Pfa 随ρc 的变化曲线Fig.5 Pfa versus ρc for the PGOS-GLRT

4.2 目标检测性能

接下来仿真验证验证所提检测方法的检测性能，针对高速机动目标可能出现的回波分布情况，主要从目标检测概率（Detection Probability,Pd）和对目标回波位置l、h估计的均方根误差（Root Mean Square Error,RMSE）对PGOS-GLRT 检测方法进行检测性能评估。其中，RMSE 的计算公式为τl为待 估计 参数。为了更好地对所提检测方法进行分析，分别在辅助数据量受限和辅助数据量充足两种仿真背景下，将所提PGOS-GLRT 检测方法、已有的PG-AMF 检测方法、广义匹配滤波方法（Generalized Adaptive Matched Filter,GAMF）以及未采用斜对称特性的广义信息准则一步GLRT（ Generalized Information Criterion One Step GLRT,GOS-GLRT）检测方法一同仿真。两种仿真背景下均取Pfa=10-4，L=10000，ρc=0.9，RNR=25 dB。需要注意的是，因为GAMF 方法不包含目标回波位置估计过程，这里只对GAMF方法的目标检测性能进行仿真分析。

首先考虑辅助数据量受限(K=Nα+1)的情况，即设K=11，图6(a)给出上述四种检测方法的Pd随SRNR变化的曲线。结果表明，所提检测方法有着最高的Pd，且所有检测方法的Pd随SRNR 的增大而逐渐提高。由图中可以看到，在Pd=0.4时，PGOS-GLRT 检测方法相较于 PGAMF 和GOS-GLRT 检测方法分别有着5.5dB 和16dB 左右的性能增益，此时GAMF 检测方法失效。图6(b)和图6(c)给出考虑了目标回波分布情况的PGOS-GLRT、PG-AMF 以及GOS-GLRT 三种检测方法对l、h估计的精确度随SRNR 变化的曲线。结果显示，所提检测方法在SRNR 较高时有着最好的估计性能，同时，斜对称的使用极大地提高了检测方法对目标回波分布情况的估计精度。以上结果证明，在辅助数据量受限的情况下，PGOS-GLRT 检测方法的目标检测性能和目标回波分布位置估计相比于其他现有同类型检测方法有着较为明显的性能优势。

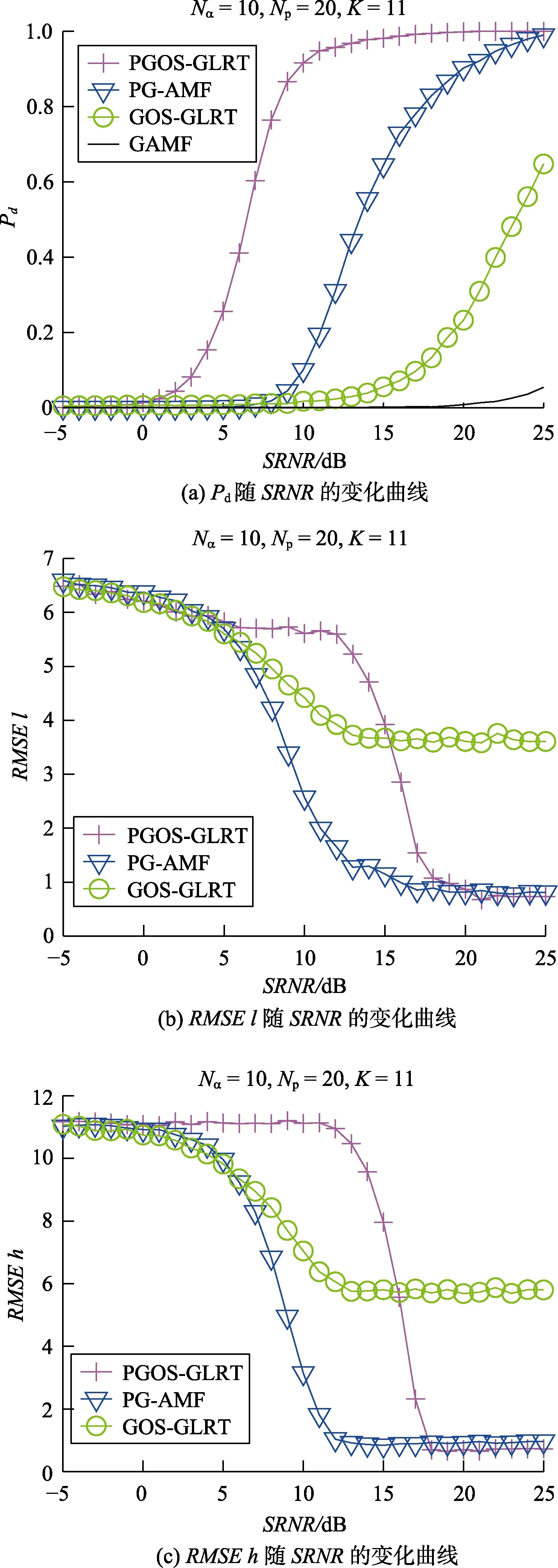
图6 辅助数据量受限时各算法检测性能Fig.6 Detection performance with small number of auxiliary samples

保持其他参数不变，改变辅助数据量为K=24，即K≥2Nα，观测辅助数据量充足时各检测方法的检测性能。由图7(a)可以看到，4 种检测方法的Pd相较于辅助数据量受限时均有所提升，且各方法之间的目标检测性能差距有所减小。但此时PGOS-GLRT 检测方法仍有着最高的目标检测性能。例如，在Pd=0.6时，PGOS-GLRT检测方法相较于 PG-AMF、GOS-GLRT 以及GAMF 检测方法分别有着1.8dB、3dB 和4dB 左右的性能增益。图7(b)和图7(c)结果说明，在辅助数据量充足的情况下，考虑目标回波分布情况的三种检测方法对l、h估计的准确度相近，此时斜对称的使用对检测方法估计目标回波位置时的精确度影响不大。最终结果表明，辅助数据量充足时，PGOS-GLRT 的检测性能优势减弱，但相比于其他同类型检测方法仍有最好的检测性能表现。

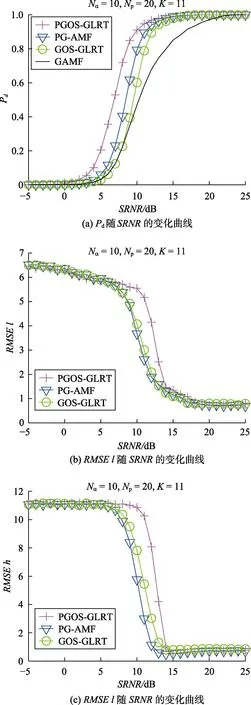
图7 辅助数据量充足时各算法检测性能Fig.7 Detection performance with sufficient number of auxiliary samples

为了进一步验证PGOS-GLRT 检测方法的检测性能，下面在未发生RCM 现象的情况下对上述4 种检测方法进行仿真分析，由于此时目标高速运动未引起RCM 现象，目标回波充满整个检测单元，这里只需观测各检测方法的dP变化。

对于辅助数据量受限条件下，仿真参数保持不变，设K=11，RMSE 由-5 dB 变化至25 dB。如图8所示，PGOS-GLRT 检测方法仍有最好的目标检测性能，在Pd=0.6时，PGOS-GLRT 较于PG-AMF 有超过10 dB 的性能增益。此时，未采用斜对称结构的GOS-GLRT 和GAMF 检测方法失效。

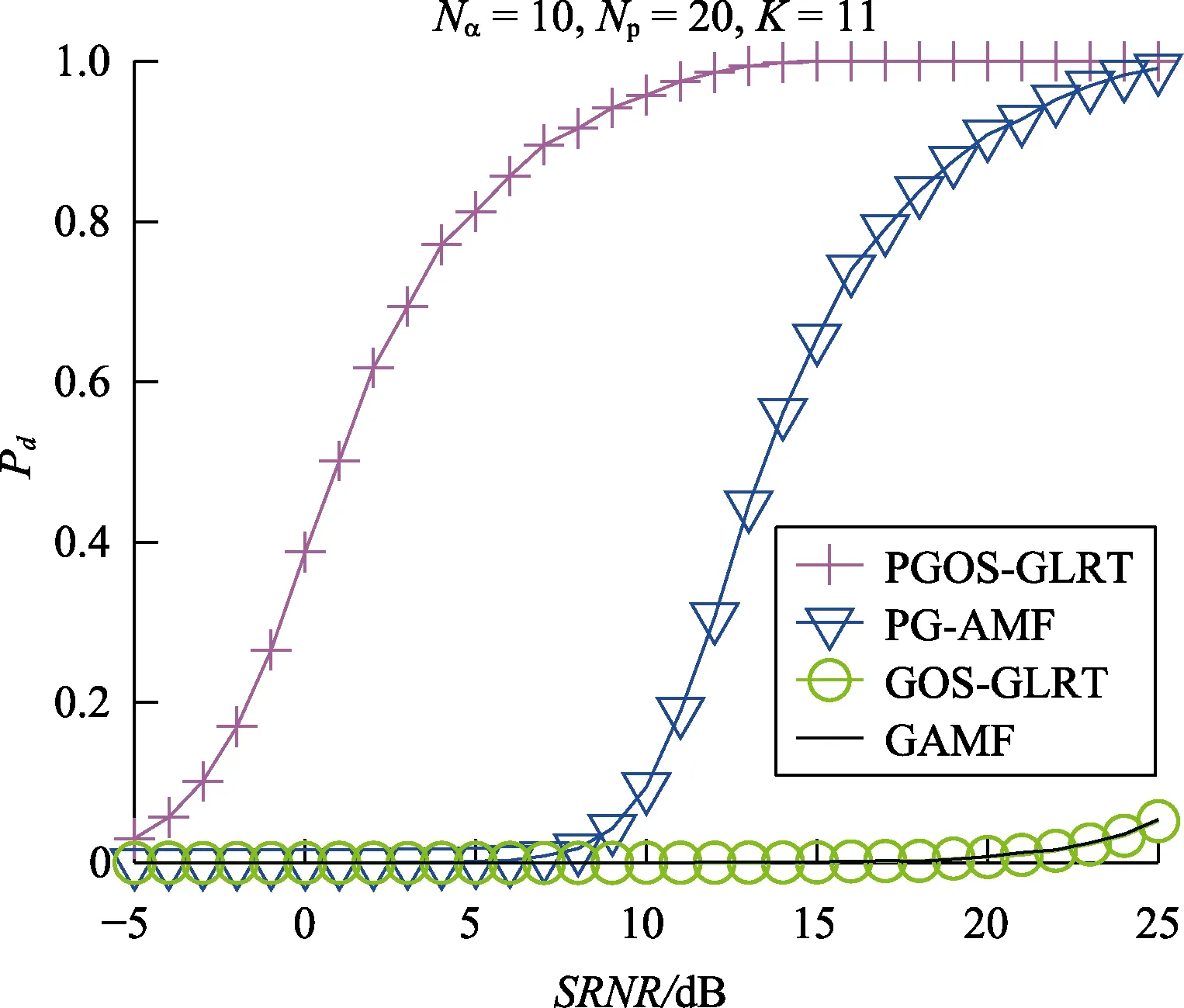
图8 辅助数据受限且未发生RCM 现象时Pd 随SRNR 的变化曲线Fig.8 Pd versus SRNR without RCM when auxiliary data is limited

接下来考虑辅助数据量充足的情况，保持其他参数不变，改变辅助数据量为K=24，观测各检测方法dP变化曲线。如图9所示，4 种检测方法目标检测性能皆提升，各检测方法之间性能差距减小，PGOS-GLRT 在这4 种检测方法中仍有最优越的检测性能表现。

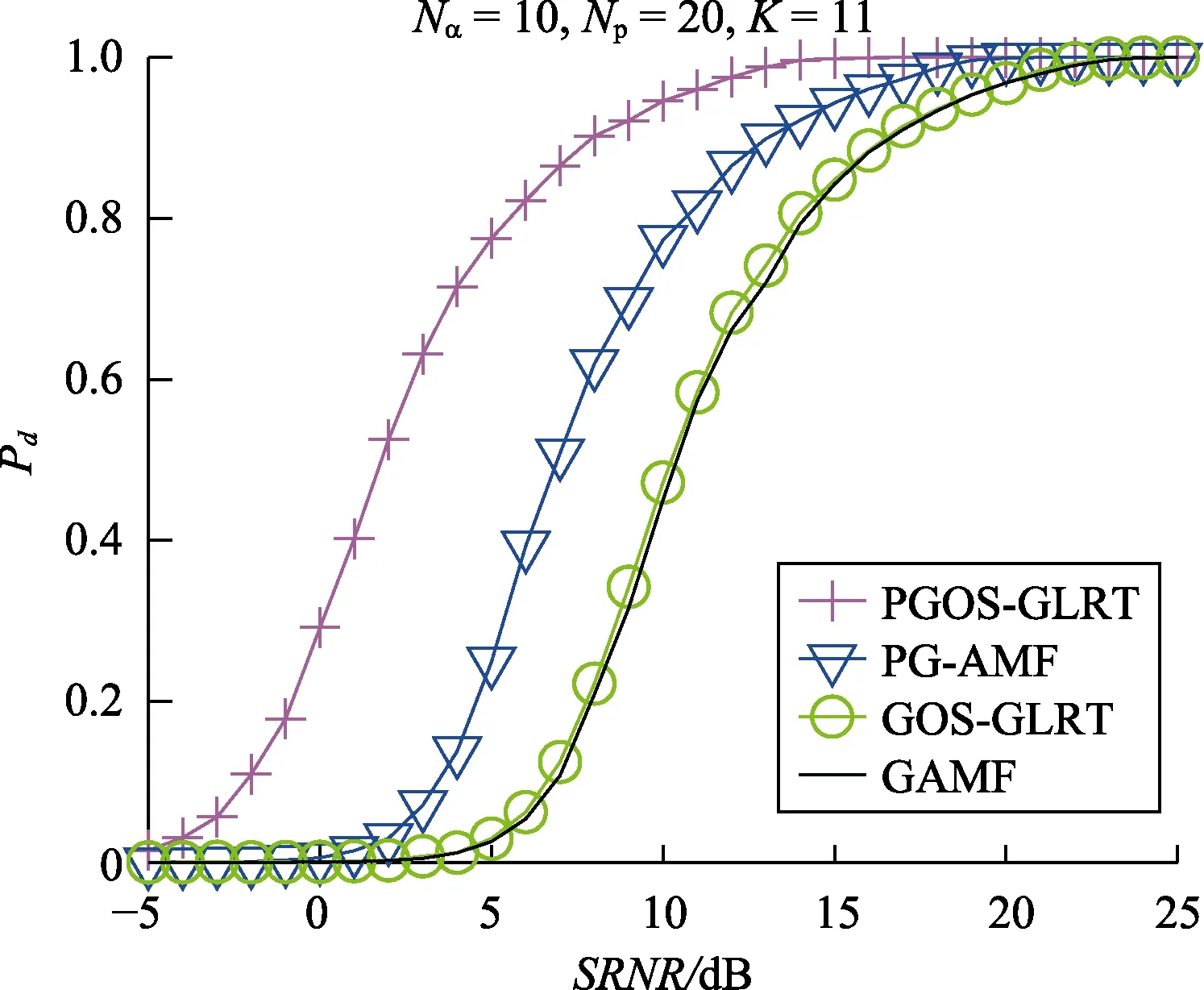
图9 辅助数据充足且未发生RCM 现象时Pd 随SRNR 的变化曲线Fig.9 Pd versus SRNR without RCM when auxiliary data is sufficient

仿真结果说明，PGOS-GLRT 检测方法在高速机动目标未发生RCM 现象时，相较于其他已有同类型检测方法仍有较明显的目标检测性能提升，并且在辅助数据量受限时有着更加明显的性能优势，有效降低了检测方法对辅助数据的依赖性。

5 结 论

本文针对高速机动目标引起的RCM 现象以及水下目标自适应检测方法在应用时常见的辅助数据不足问题，提出一种适用于高速机动目标的斜对称广义似然比检测方法。考虑到目标高速运动引起的RCM 现象，采用多元假设检验模型，准确描述目标回波位置，同时采用干扰协方差的斜对称特性降低辅助数据需求量。最后，基于一步GLRT 准则，联合使用待检测数据和辅助数据估计所有未知参数并推导得到PGOS-GLRT 检测方法的检测统计量。仿真结果表明，该检测方法具有CFAR 特性，且所提检测方法在检测高速机动目标时，相比于已有的PG-AMF、GAMF 检测方法有着显著的性能优势，尤其在辅助数据受限这种非理想情况下，性能优势更为明显。未来的研究拟将所提出的检测方法框架扩展到背景环境非均匀或背景干扰非高斯的情况。