船载雷达随机振动疲劳寿命分析

马志毅，张 彬，楚雪梅

船载雷达随机振动疲劳寿命分析

马志毅，张 彬，楚雪梅

（北京遥测技术研究所北京 100076）

振动疲劳作为结构破坏失效形式之一，正日益得到重视。传统的船载雷达设备设计往往仅考虑静强度，从而导致结构抵抗疲劳破坏的能力不足。从模态分析的角度入手，利用模态叠加法进行随机振动分析，得到结构的各向应力功率谱密度。在此基础上进行基于Von Mises应力的谱分析，并分别从宽带和窄带过程的角度进行了疲劳寿命估算，最后对某船载雷达进行了随机振动疲劳分析。结果表明，船载雷达结构在满足静强度条件下，不一定能够满足抗疲劳性能要求。从模态振型分析的角度改进了结构设计，分析验证表明，改进后结构能够满足随机振动疲劳寿命要求。

振动疲劳；模态分析；谱分析；疲劳寿命

引言

船载雷达设备由于受海况、航速、机动等变化的影响，通常承受较严酷的随机振动载荷，振动疲劳破坏已成为其主要的结构失效形式。一般来说，船载雷达结构设计往往仅考虑静强度，导致其无法承受有随机振动环境引起的往复交变载荷，从而引起疲劳失效。船载雷达一旦发生损伤破坏，不仅会影响海洋监测活动，还可能危及航海安全。因此，在船载雷达结构设计时，随机振动疲劳寿命分析十分重要。

随机振动疲劳分析方法主要包括时域法和频域法。时域法是比较成熟的方法，在获得应力或应变的时域数据的基础上，采用一定统计方法（一般为雨流计数法）获得载荷循环次数，并利用SN曲线，进行累计损伤计算[1]。然而，在设计初期，很难获得相应的基础数据，因此，时域法很难得到广泛应用。而频域法是利用应力的功率谱密度进行应力循环次数估计，在产品的三维数字样机阶段，可以通过仿真分析得到相应的基础数据，因此较多的学者从事这方面研究，并取得了一定的成果[2,3]。王文伟、程雨婷采用Steinberg提出的高斯三区间法对电动汽车电池箱进行随机振动疲劳分析[4]，该方法假设等效应力服从高斯分布，且忽略了三区间外发生的应力，计算精度不高。目前，广泛采用的频域法是Dirlik法，该方法利用PSD的四个惯性矩，得到了应力概率密度函数的封闭解。Bishop对该方法进行了理论论证，并验证了该方法的精确性。刘龙涛、李传日、程祺采用Dirlik法对某机载设备进行随机振动疲劳寿命分析[5]，但其采用单向应力功率谱密度进行分析计算，忽略了各向应力的耦合作用。贺光宗、陈怀海、贺旭东推导的基于Von Mises应力的功率谱密度公式[6]，但忽略了各正应力之间的互功率谱密度。

综上所述，在结构设计过程中进行振动疲劳可靠性分析十分必要。目前已有一些针对振动疲劳破坏的分析方法，但大多基于单轴应力的功率谱密度进行，通常情况下，由于结构的复杂性，应力状态往往是多轴的。因此，本文在有限元分析的基础上，利用结构各向应力的功率谱密度推导了Von Mises应力的功率谱密度，这样就利用等效应力综合考虑了各向应力的复合效应。在此基础上，分别从窄带和宽带过程，进行疲劳寿命估算。最后进行了某船载雷达随机振动疲劳分析，验证了该方法的工程实用性和准确性。

1 机械结构动力学基本原理

1.1 定位原理

对一般机械系统可以建立动力学方程：

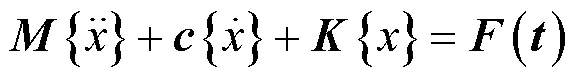
对于自由振动的情况，忽略阻尼力影响，可以得到：

设特解

得到：

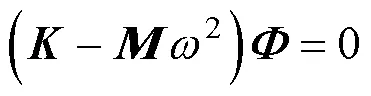
2 基于Von Mises应力的谱分析

2.1 Von Mises应力功率谱密度计算

Von Mises应力准则认为畸变能密度是引起屈服的主要因素，一般针对塑性材料强度校核，其时域定义如式（5）所示：

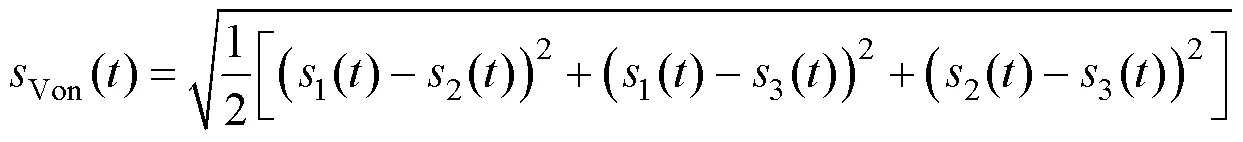
船载雷达设备结构的应力响应一般为三向应力状态，这样式（5）变为：

其中，为应力向量，定义如式（7）所示：

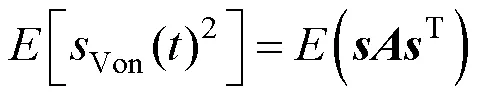
对式两边进行傅里叶变换，可以得到：

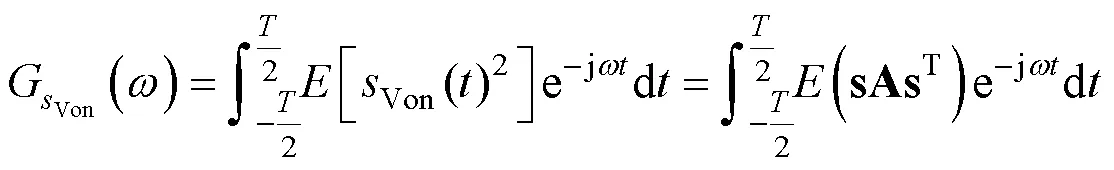
因此，Von Mises应力可转化成各向应力的自功率谱密度和互功率谱密度的叠加。则有：

各向正应力和剪应力的功率谱密度可以很方便地通过有限元仿真得到，而互功率谱密度无法直接计算，因此，互功率谱密度是Von Mises应力功率谱密度计算的关键环节。

2.2 应力分量的互功率谱密度计算

由于互功率谱密度是互相关函数的傅里叶变换，则得：

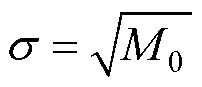
① 窄带情况下，应力服从Rayleigh分布，其表达式如式（18）所示：

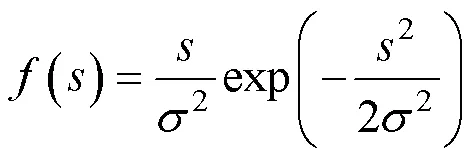
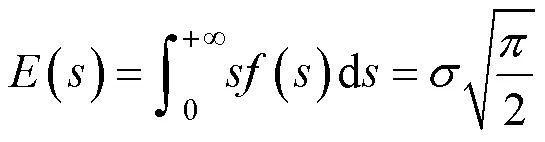
② 宽带情况下，Dirlik法对应力概率密度函数描述如式（20）所示：

式中，各参数定义如式（21）所示：

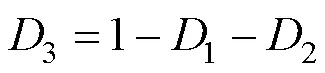
将式（22）代入式（13）可以得到互功率谱密度，如式（23）所示：

将式（22）代入式（10）可以得到Von Mises应力的功率谱密度。

3 基于功率谱密度的随机振动疲劳寿命分析

得到Von Mises应力的功率谱密度后，根据2.2节，可以分别获得窄带和宽带过程的Von Mises应力功率谱密度函数，在此基础上，就可以进行随机振动疲劳寿命分析。通用的疲劳寿命分析方法是miner线性累计损伤法则，公式如式（25）所示:

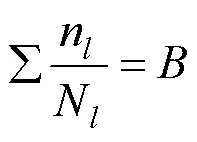
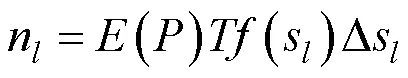
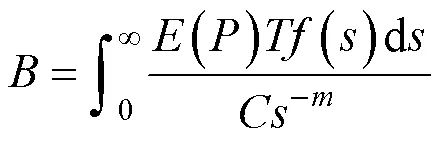
当Von Mises应力为窄带过程，用Rayleigh分布对Von Mises应力概率密度函数进行描述，将式（18）代入式（28）可得

当Von Mises应力为宽带过程，用Dirlik法对Von Mises应力概率密度函数进行描述，将式（20）代入式（28）可得

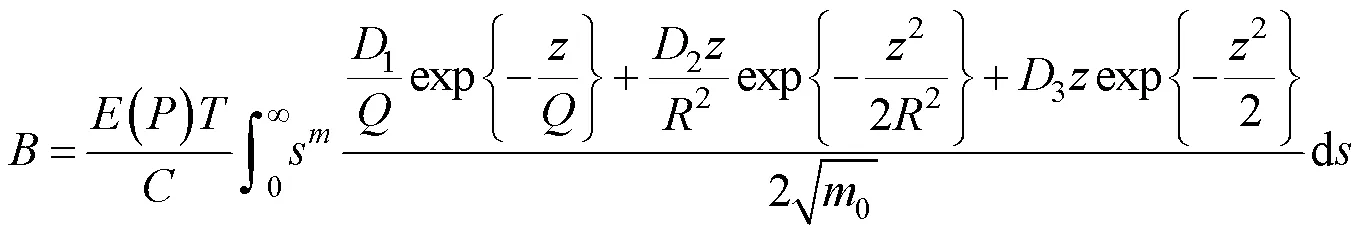
4 某船载雷达随机振动疲劳寿命分析

4.1 模态分析

某船载雷达结构由鞭状天线、磁天线和支架组成，整体结构呈现出悬臂支撑形式，如图1所示。

将天线底部约束进行模态分析，结果如图2～图5所示。

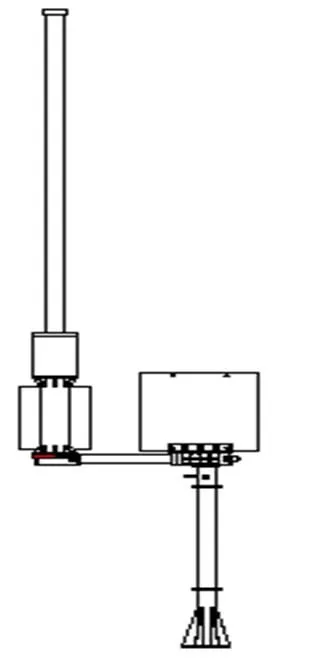
图1 船载雷达结构图

图2 第一阶振型图

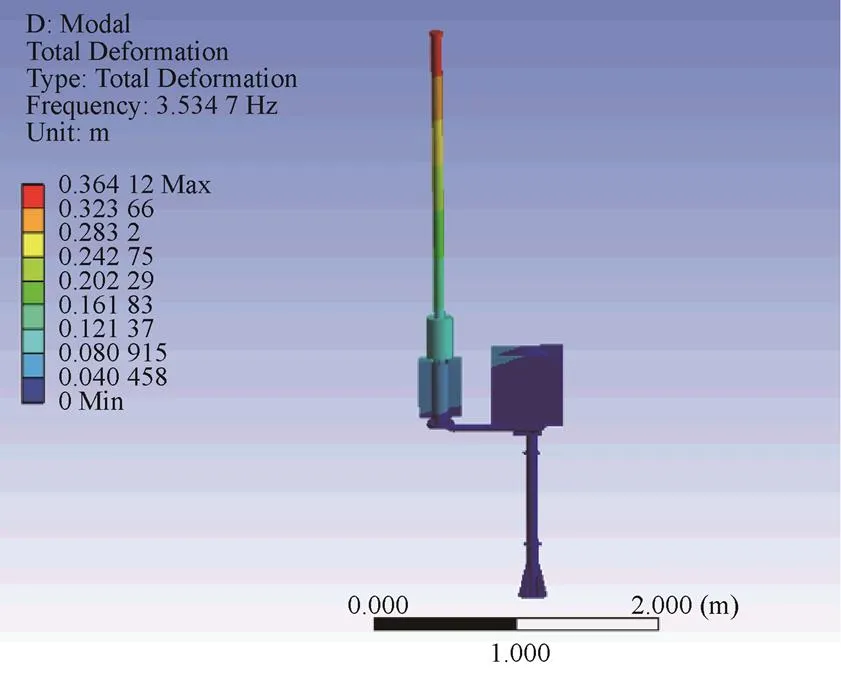
图3 第二阶振型图

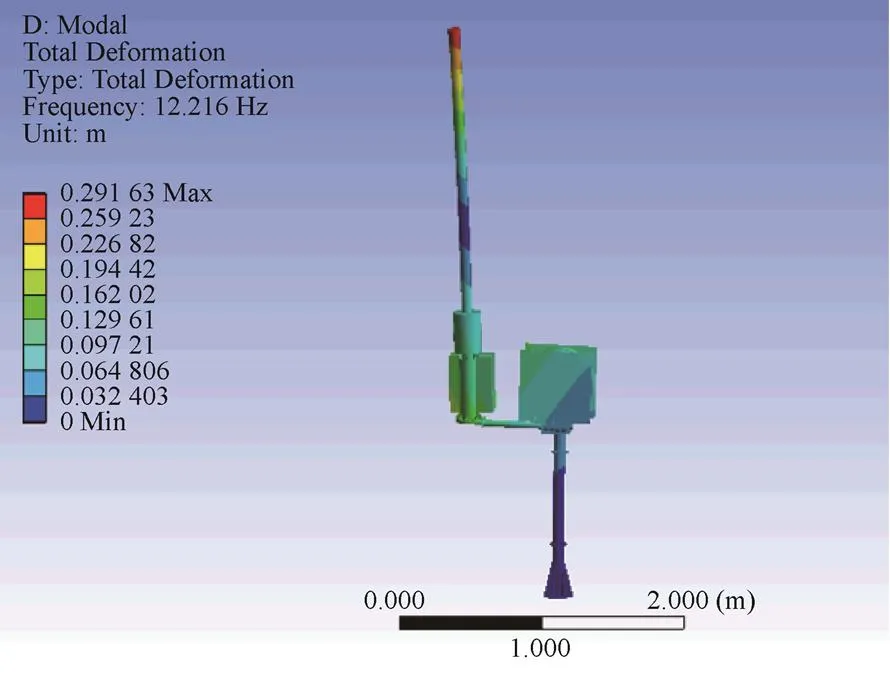
图4 第三阶振型图

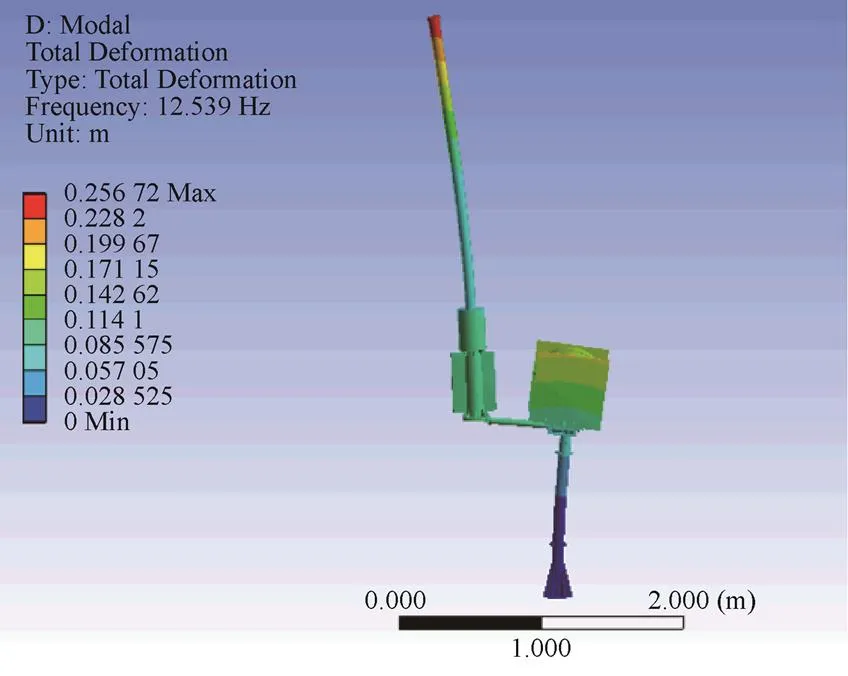
图5 第四阶振型图

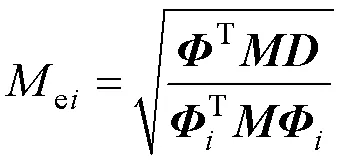
Ansys的振型向量的归一化形式如式（32）所示：

将式（32）代入式（31），得

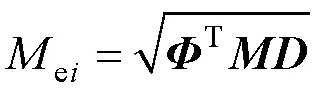
雷达的模态分析结果见表1。

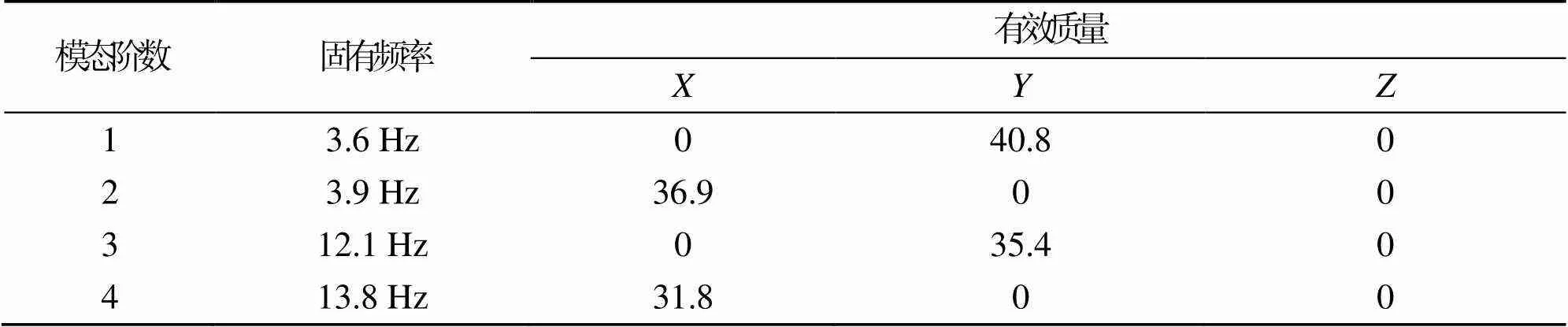
表1 模态分析结果表

表1列出了前四阶模态的固有频率和有效质量，可以看出前四阶模态固有频率非常小；前四阶模态的有效质量均集中在和方向，即主振方向为方向和方向，这与振型图完全复合。综上所述，该船载雷达的整体刚度较差，并且向和向是其中最薄弱的两个刚度方向。

4.2 原结构随机振动疲劳寿命分析

舰船振动是由于自然环境（海浪、风）激励，强迫激励（螺旋桨转动、往复机械运动）等引起的，在没有实测数据时，采用GJB150.16A推荐的振动试验条件，量级如图6所示，三个正交轴每个轴向持续2 h。

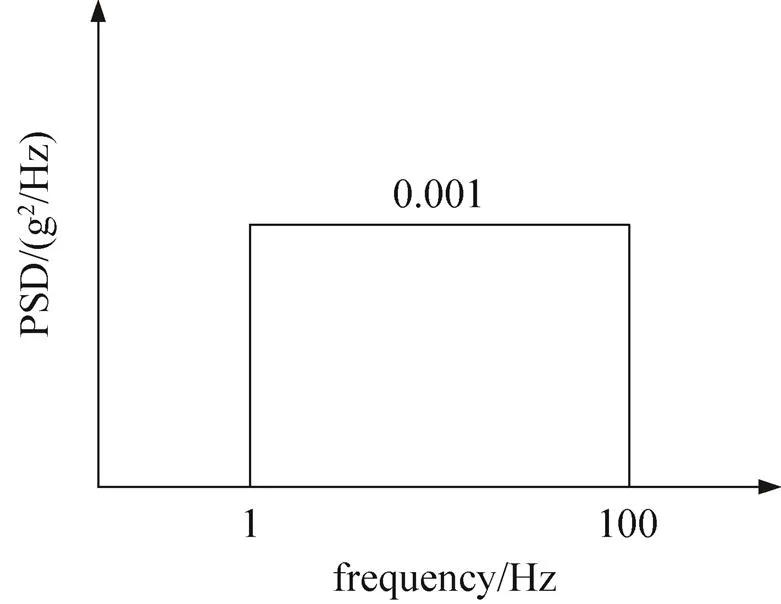
图6 振动试验条件

仿真计算发现在方向载荷作用下，会产生最大应力。最大应力分布如图7所示。

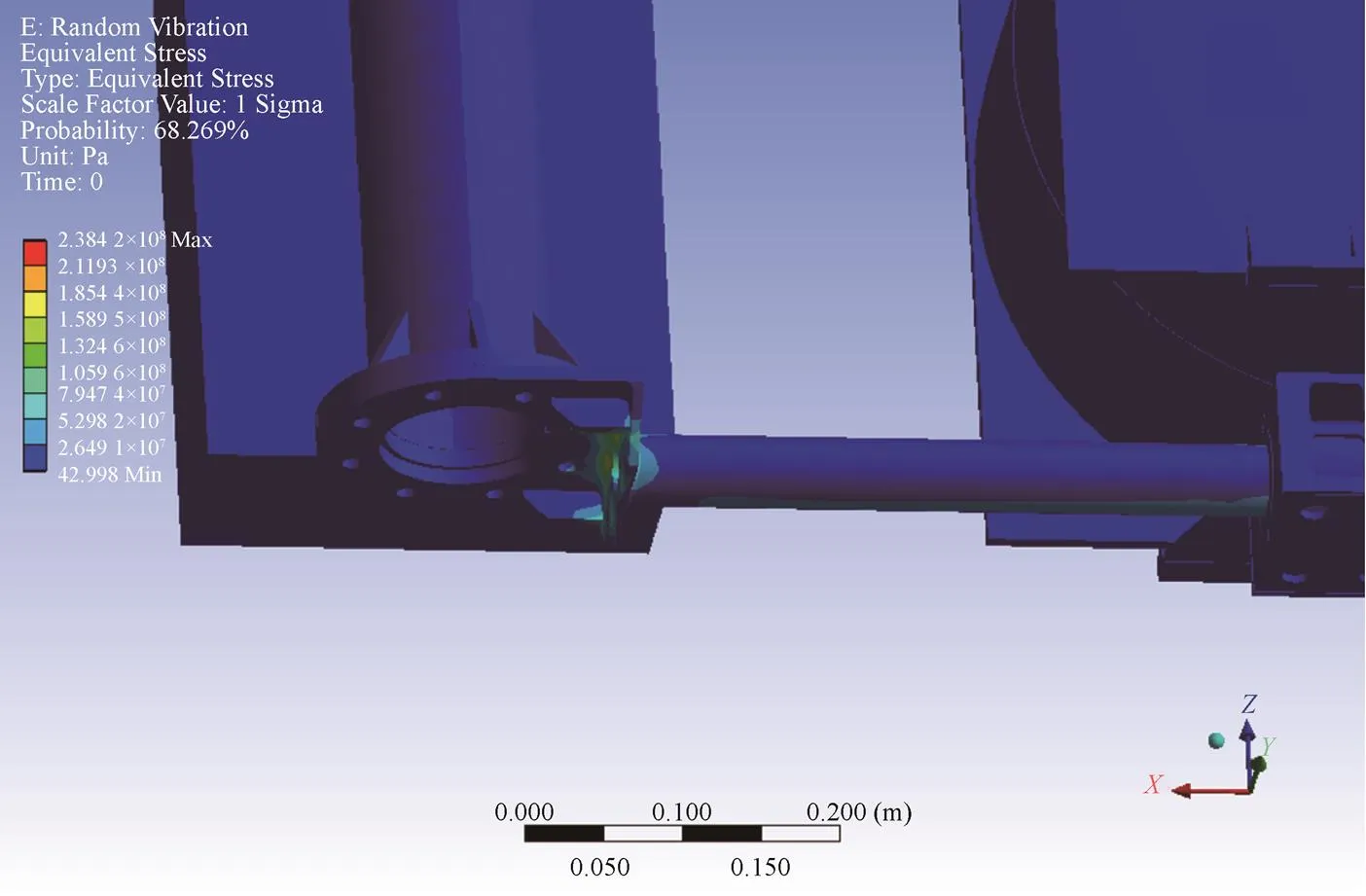
图7 最大应力分布位置图（初始结构）

通过仿真分析得到最大应力出现在天线支架根部，能够满足静强度要求。提取该处的各方向的应力功率谱密度，计算得到Von Mises应力功率谱密度如图8所示。

4.3 改进结构随机振动疲劳寿命分析

根据仿真分析计算结果，进行结构设计改进。在天线根部进行加固设计，改进结构如图9所示。仿真分析计算得到最大应力分布如图10所示。

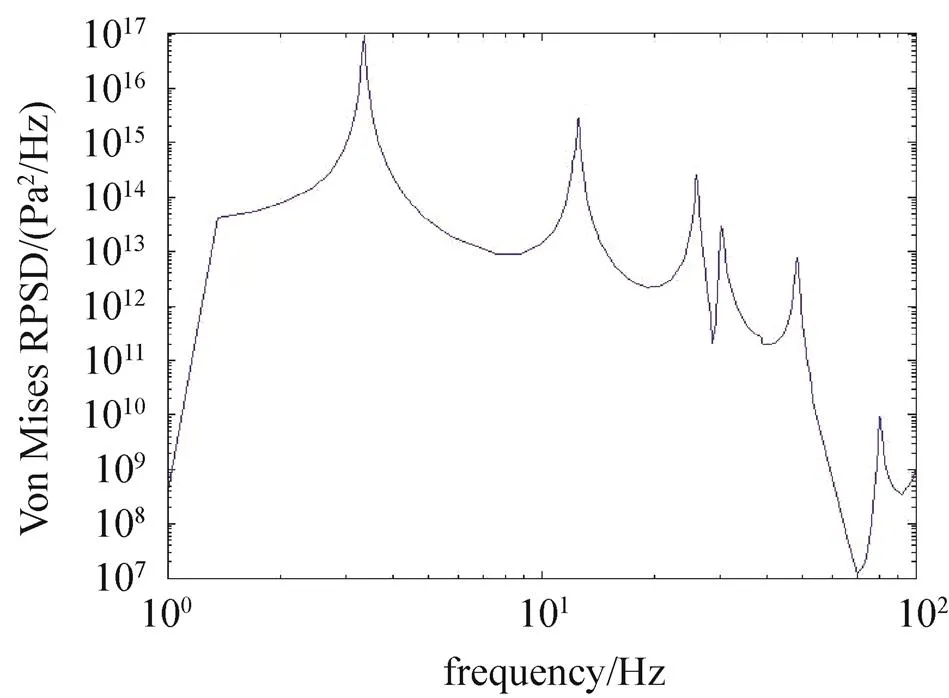
图8 应力功率谱密度图（初始结构）

可以看出最大应力值降低到93 MPa，最大应力分布变到支架顶端。提取该处的各方向的应力功率谱密度，计算得到Von Mises应力功率谱密度如图11所示。

图9 改进结构图

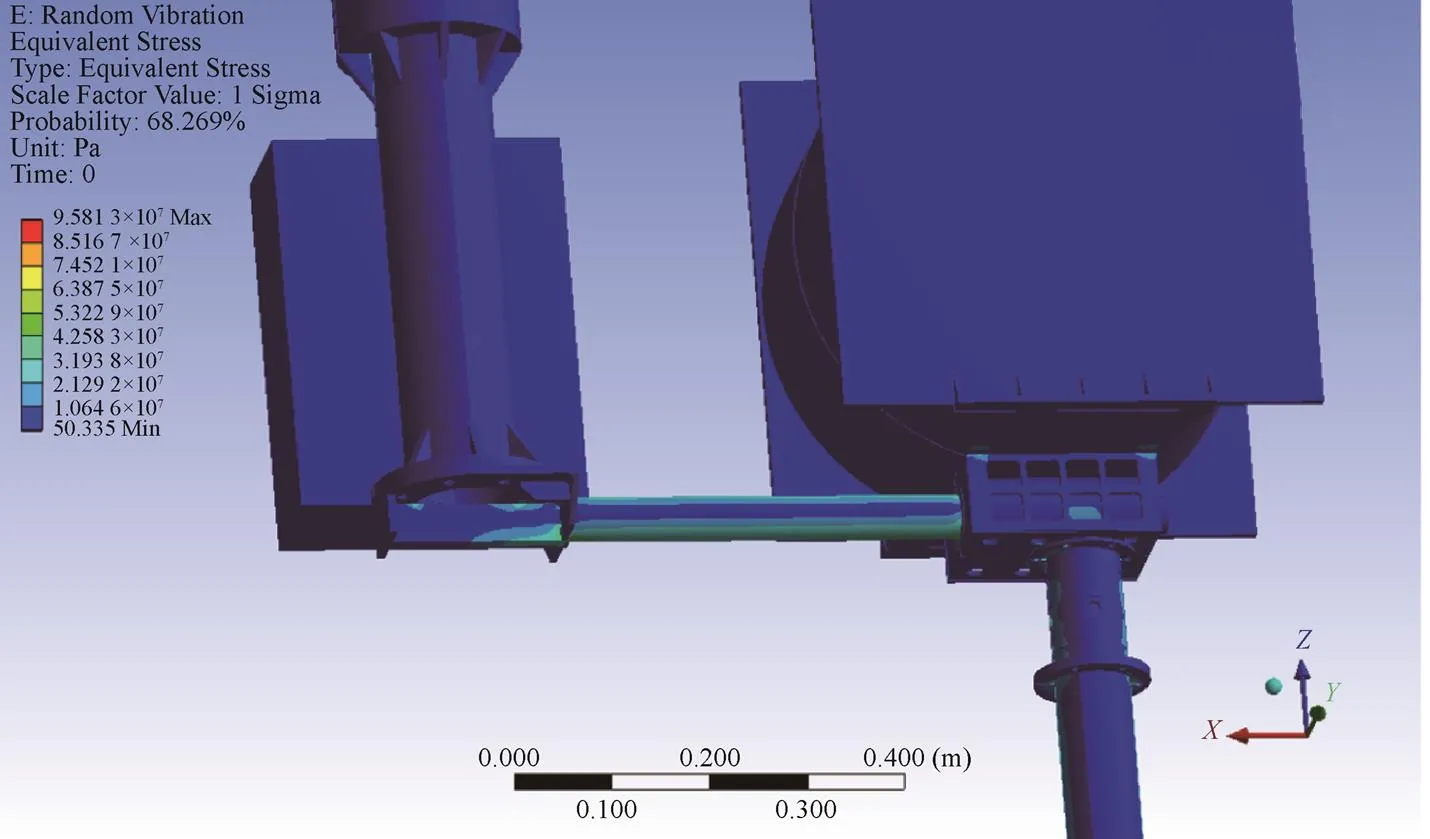
图10 最大应力分布位置图（改进结构）

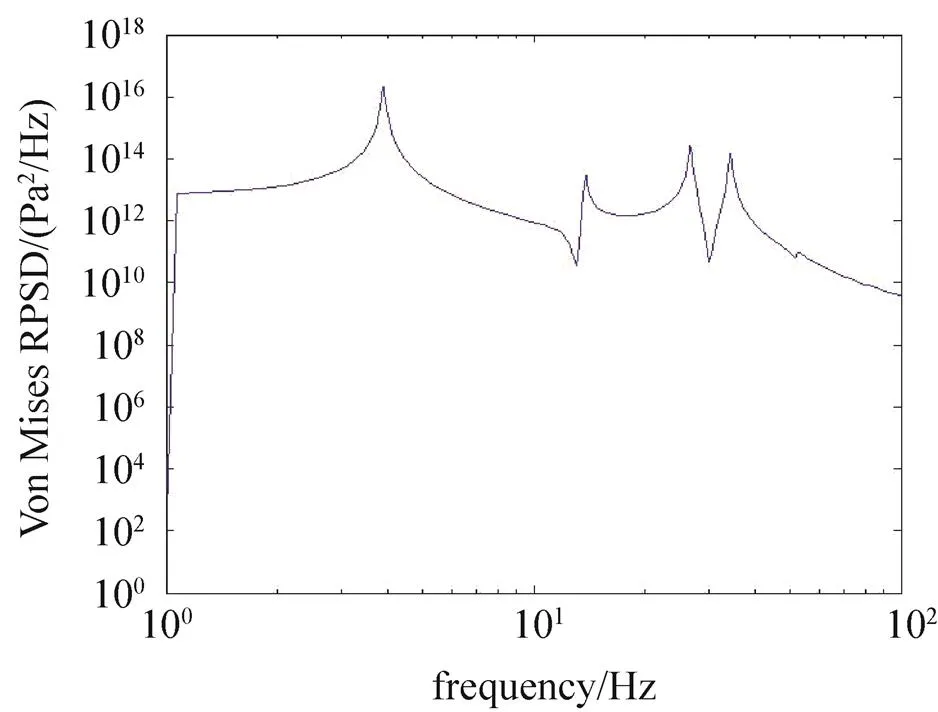
图11 应力功率谱密度图（改进结构）

4.4 计算方法对比

目前随机振动疲劳寿命的计算方法，主要有高斯三区间法、Dirlik法。采用改进前结构模型，将这两种方法和本文方法进行对比分析，见表2。

通过对比发现高斯三区间法计算复杂度最低，Dirlik法次之，本文方法最高，但是高斯三区间振动频率的取值较保守，导致损伤系数计算结果偏低。Dirlik法只采用单向应力进行计算，也会导致损伤系数计算结果偏低。本文方法相对来说虽然复杂度较高，但是计算精度较高，与试验结果相符。

表2 不同方法计算对比表

5 结束语

本文在有限元分析的基础上，利用结构各向应力的功率谱密度推导了Von Mises应力的功率谱密度，利用等效应力综合考虑各向应力的复合效应。在此基础上，分别从窄带和宽带过程，进行疲劳寿命估算。最后针对某船载雷达进行随机振动疲劳分析，验证了该方法的工程实用性和准确性。船载结构在满足静强度条件的前提下有可能不满足寿命要求，在改进结构后，结构抗疲劳损伤能力显著提高，能够满足寿命要求。

[1] 郭小鹏, 沙云东, 张军. 基于雨流计数法的随机声疲劳寿命估算方法研究[J]. 沈阳航空工业学院学报, 2009, 26(3): 10–13, 9.

GUO Xiaopeng, SHA Yundong, ZHANG Jun. Random fatigue life estimation based on rain-flow counting method[J]. Journal of Shenyang Institute of Aeronautical Engineering, 2009, 26(3): 10–13, 9.

[2] 吕彭民. 基于频域法的结构疲劳寿命预测方法研究[J]. 山东交通学院学报, 2006, 14(3): 1–5.

LYU Pengmin. A method of structural fatigue life prediction on the basis of frequency domain[J]. Journal of Shandong Jiaotong University, 2006, 14(3): 1–5.

[3] 王德如, 杨和振. 海上风机支撑结构的时域和频域疲劳对比研究[J]. 舰船科学技术, 2017, 39(4): 74–78, 99.

WANG Deru, YANG Hezhen. Time-domain ang frequency-domain fatigue analysis of offshore wind turbine support structure[J]. Ship Science and Technology, 2017, 39(4): 74–78, 99.

[4] 王文伟, 程雨婷, 姜卫远, 等. 电动汽车电池箱结构随机振动疲劳分析[J]. 汽车工程学报, 2016, 6(1): 10–14.

WANG Wenwei, CHENG Yuting, JIANG Weiyuan, et al. Random vibration fatigue analysis of electric vehicle battery box[J]. Chinese Journal of Automotive Engineering, 2016, 6(1): 10–14.

[5] 刘龙涛, 李传日, 程祺, 等. 某结构件的随机振动疲劳分析[J]. 振动与冲击, 2013, 32(21): 97–101.

LIU Longtao, LI Chuanri, CHENG Qi, et al. Random vibration fatigue analysis of a structure[J]. Journal of Vibration and Shock, 2013, 32(21): 97–101.

[6] 贺光宗, 陈怀海, 贺旭东. 一种多轴向随机激励下结构疲劳寿命分析方法[J]. 振动与冲击. 2015, 34(7): 59–63.

HE Guangzong, CHEN Huaihai, HE Xudong. Vibration fatigue life prediction method for structure under multi-axial random excitations[J]. Journal of Vibration and Shock, 2015, 34(7): 59–63.

Fatigue life prediction of shipborne radar based on random vibration analysis

MA Zhiyi, ZHANG Bin, CHU Xuemei

（Beijing Research Institute of Telemetry, Beijing 100076, China）

As one of the failure forms of structure, vibration fatigue is getting more and more attention. However, the traditional design of shipborne radar only considers the static strength, which leads to the lack of the ability to resist fatigue damage. From the perspective of modal analysis, this paper uses modal superposition method for random vibration analysis, so as to obtain the power spectral density of structural stress in all directions. On this basis, the spectrum analysis based on Von Mises stress is carried out, and the fatigue life is estimated from the perspective of broadband and narrowband processes respectively. Finally, the random vibration fatigue analysis of a shipborne radar is carried out. The results show that the structure of shipborne radar can not meet the requirements of anti fatigue performance under the condition of static strength. Then, from the perspective of modal analysis, the structural design is improved. Finally, through the analysis, it is concluded that the improved structure can meet the requirements of random vibration fatigue life.

Vibration fatigue; Modal analysis; Spectrum analysis; Fatigue life

O324

A

CN11-1780(2022)05-0111-09

10.12347/j.ycyk.20210815001

马志毅, 张彬, 楚雪梅.船载雷达随机振动疲劳寿命分析[J]. 遥测遥控, 2022, 43(5): 111–119.

DOI：10.12347/j.ycyk.20210815001

: MA Zhiyi, ZHANG Bin, CHU Xuemei. Fatigue life prediction of shipborne radar based on random vibration analysis[J]. Journal of Telemetry, Tracking and Command, 2022, 43(5): 111–119.

2021-08-15

2021-12-28

马志毅 1988年生，硕士，工程师，主要研究方向为结构热力学设计。

张 彬 1981年生，博士，研究员，主要研究方向为雷达总体设计。

楚雪梅 1991年生，硕士，工程师，主要研究方向为结构热力学设计。

(本文编辑：杨秀丽)