系留翼伞刚柔混合模型控制方法探索研究*

刘松林，安 朝，朱 靖，谢长川，徐 萍

系留翼伞刚柔混合模型控制方法探索研究*

（1 深圳市百川融创科技有限公司 深圳 518110 2 北京航空航天大学 北京 100191 3 91977部队 北京102299）

系留翼伞可借助风力长期滞空，相比系留无人机具有抗风能力强、载荷重量大、电能消耗低、侦察视距远等优点，由于系留翼伞具有刚柔耦合特性，控制系统设计难度高，目前还缺乏有效的控制模型，技术上还不够成熟，制约了新型滞空飞行平台的应用。从系留翼伞刚柔耦合动力学建模、系留翼伞非定常气动力建模、系留翼伞刚柔混合状态空间建模、系留翼伞刚柔混合控制技术实现等四个方面探索了基于刚柔混合模型的系留翼伞控制方法，并验证了该方法的有效性。

系留翼伞；刚柔耦合；耦合控制；仿真试验

引言

系留翼伞可以借助风力长期滞空，相比系留无人机具有抗风能力强、载荷重量大、电能消耗低、载荷侦察视距远等优点，是一款适应大风环境的新型长期滞空侦察监视平台系统。系留翼伞主要由伞翼、有效载荷舱及绳索三部分组成。伞翼受到非定常气动载荷作用产生明显的变形；有效载荷舱处于柔性悬挂状态，其受力状态及运动形式与传统系留翼伞差别显著；绳索在伞的作用下发生牵引运动及横向振动、纵向振动、回转振动等，影响因素多，运动形式复杂[1-3]。因此，传统基于线性小变形假设的分析方法无法准确描述系留翼伞的载荷和变形特点，更无法反映其真实物理情景和力学本质。可以从飞行动力学和弹性力学统一化的思想出发，在两门学科的交叉领域开展研究工作，研究提出飞行动力学和弹性力学的统一化建模思路，并采用PID方法设计系统控制律，形成工程适用性较强的控制系统。

1 系留翼伞刚柔混合动力学建模

系留伞翼控制过程可以先借鉴经典非线性有限元方法中的梁单元运动关系[4-6]，研究绳索收放系统的启动、停止、收放速度以及控制面位置、作动速度等因素，都将显著影响伞翼系统动力学特性。需要针对伞翼系统建立动力学模型，确保所建立的伞翼系统结构动力学模型也是稳定性分析、控制设计的先期基础。

考虑伞翼气动载荷，绳索上的分布式定常/非定常载荷及系留翼伞对绳索的静/动力学作用，结合飞行动力学理论[7-9]可建立如下形式的系留翼伞刚柔耦合飞行动力学方程（1）：

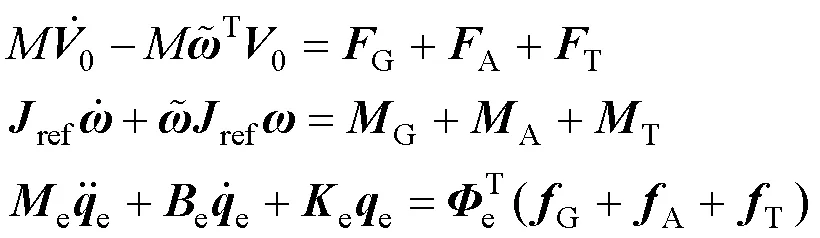
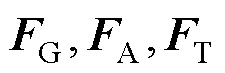
刚柔耦合系统小扰动方程（2）可以表示为：

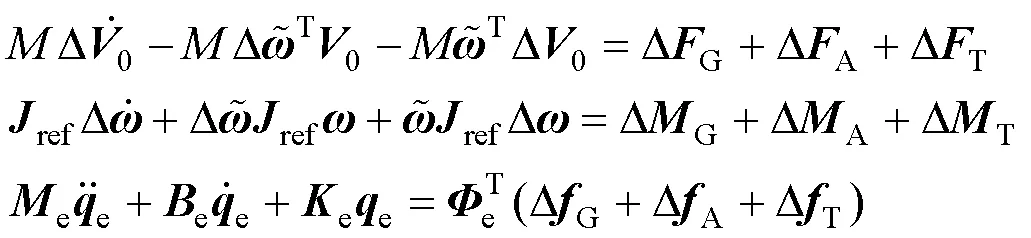
气动力方程（3）可写为：

综合结构动力学模型、气动载荷方程及外力载荷方程可得刚柔耦合系统动力学模型为方程（4）、（5）、（6）：

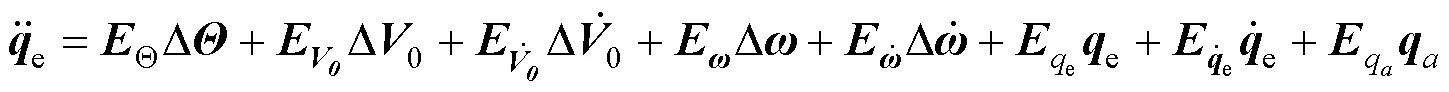
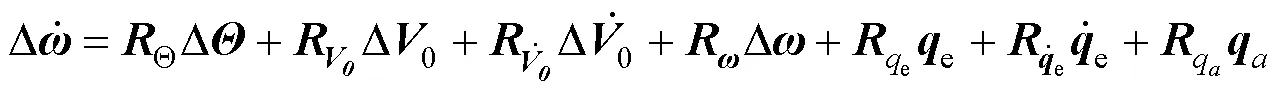
动力学响应计算方面，采用数值计算方法计算载荷分布及响应情况。稳定性分析方面，对系统动力学模型进行线性化[10-12]，给出系统失稳条件及判断方法准则。在动力学模型基础上，研究飞机的牵引速度、绳索长度、收放速度等因素对系统运动形式和稳定性的影响规律，分析伞翼控制面相关参数对稳定性影响规律，指导系统设计。

2 系留翼伞非定常气动力学建模

系留翼伞所受外载主要包括绳索系留拉力、有效载荷舱提供的外力及气动载荷，其中气动载荷数值较大，非线性因素明显，缺乏准确建模方法，可信的气动力模型对于系留翼伞动力学分析具有重要意义。系留翼伞属典型的大柔性薄膜结构，变形大，非线性因素明显且工作环境复杂，传统气动力方法不适用，且CFD方法在实用上存在较大困难，需要建立能够计算该类大柔性薄膜结构的气动力模型，同时考虑到稳定性分析及控制系统分析的需要，气动力模型需要能够融入控制模型设计。据此，可以采用兼顾计算效率及计算准确度的状态空间涡格法[13-15]建立系留翼伞气动力模型，估算飞行及操纵导数。有效载荷舱可以按照刚体处理，气动力计算较为常规，需要重点解决的是伞翼部分气动力计算理论。针对翼伞在给定形状及工况下建立气动面，划分单元气动网格。根据Biot-Savart定律计算涡格法诱导系数矩阵，在控制点处满足Neumann边界条件[13,16]，结合尾涡输运关系建立状态空间形式气动力控制方程。由于翼伞系统运动参数信息包含在气动力方程边界条件中，对边界条件各运动参数求导，即可给出相关飞行导数及操纵导数信息。

状态空间涡格法控制方程（7）可表示为：

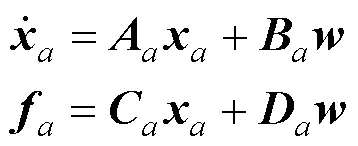
可以给出系留翼伞飞行气动导数及操纵导数为方程（9）：

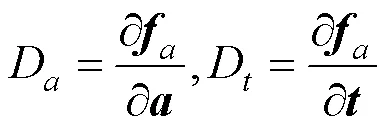
气动力建模、飞行气动导数及操纵导数的求解为系留翼伞飞行动力学建模提供基础。该方法也可预留CFD或试验气动导数数据引入接口，可以根据精度更高的气动力数据修正气动力模型。

3 系留翼伞刚柔混合状态空间建模

系留翼伞气动环境和飞行状态复杂，系统非线性因素明显，其动力学特性与传统工程系统有显著不同。能够保持稳定，具备操纵机动能力是系留翼伞正常工作的必要条件，因此需要开展相关系统的控制律设计。PID控制是最早发展的经典控制理论之一，具有算法简单、鲁棒性好、可靠性高的优点，被广泛应用于理论研究及实际工业应用中[17]。PID控制将系统输出与参考输入间的偏差经比例（P）、积分（I）及微分（D）运算后通过线性组合构成控制量，对被控对象进行控制。典型的PID控制原理如图3所示。

在建立动力学模型及稳定性分析的基础上，开展系留翼伞系统控制律设计研究。控制方案设计方面，考虑绳索控制方式，以拉绳自由度为主要作用量。PID系统的传递函数可表示为方程（10）：

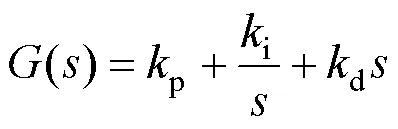
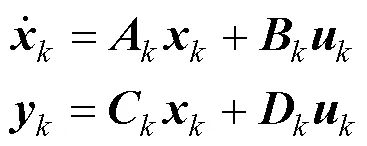
PID控制器方法只能将受控对象看作单输入单输出系统处理，操纵通道的控制律设计彼此独立。因此，针对多输入多输出系统的控制律设计，可将控制律设计简化为多个单输入单输出系统的控制律设计。以系留翼伞稳定性线化状态为例，系统状态空间模型为方程[18-20]（12）：

拉绳控制环节状态空间模型为方程（13）：

综上可得系留翼伞开环系统状态空间模型为方程（14）：

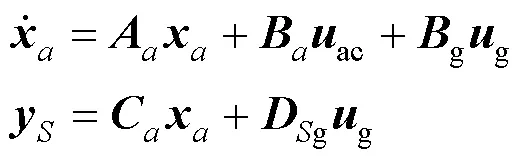
则系留翼伞闭环系统状态空间模型为方程（15）：

根据系留翼伞闭环系统状态空间模型，通过PID控制律给出典型状态下的控制环节，分析控制系统性能，进行时域仿真研究，保证系统稳定及信号跟随。计算不同给定外界激励下的系统动响应水平，分析系统抗风性能。计算不同机动输入信号下的系统动响应时域响应，分析系统操纵性能。同时考虑到系留翼伞工作环境多变及运动状态复杂的特点，开发相应的自适应控制律，以保证在全工作阶段，系统稳定可控。

4 系留翼伞刚柔混合控制技术实现

系留翼伞系统通过逻辑关系，建立刚柔混合系留翼伞动力学模型及控制律设计研究途径如图1所示。

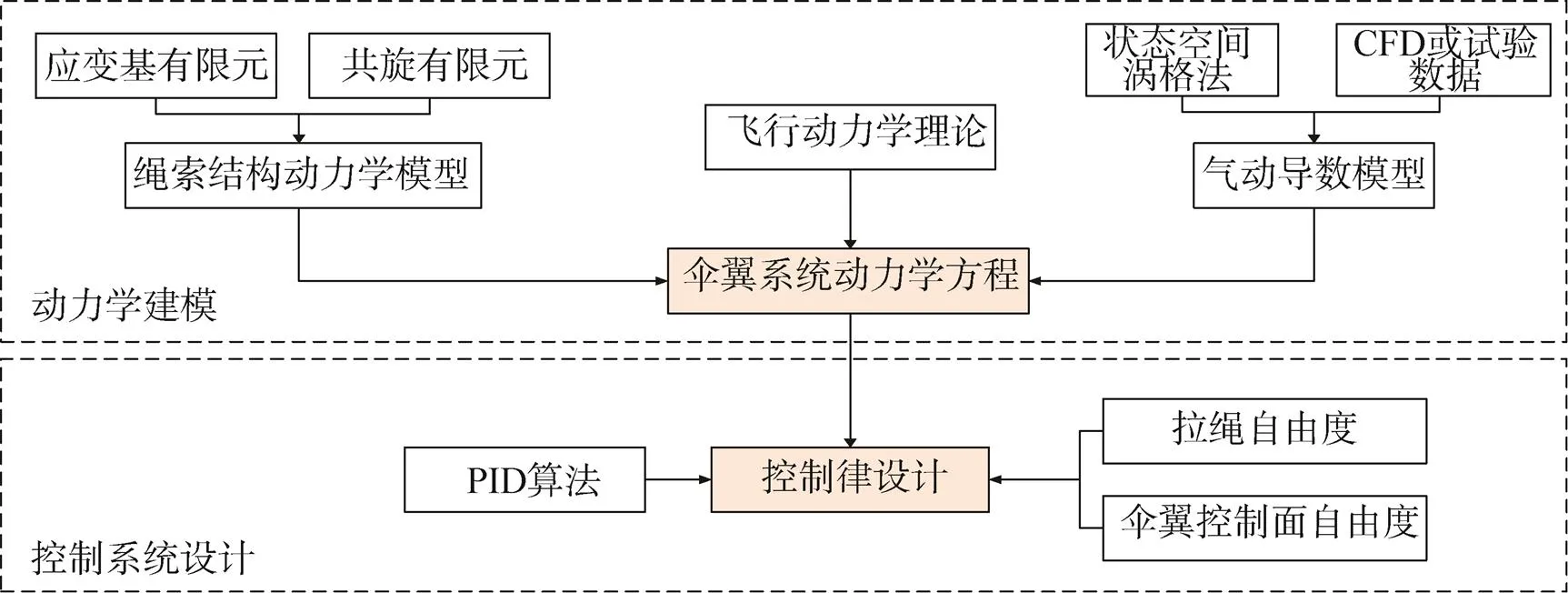
图1 刚柔混合系留翼伞动力学建模与控制技术实现方法

将系留翼伞分解为大柔性绳索单元及伞翼面膜结构单元，采用非线性有限元模型建立结构模型。由于伞翼的柔性特点，气动与伞翼具有强烈的非线性耦合作用，需考虑工程适用的理论方法计算非定常气动力，因此，采用状态空间涡格法。该方法基于势流理论建立，适用于低速情况，气动力的非线性主要源于结构大变形引起的气动边界条件改变。当结构变形较大时，需要采用几何精确的气动边界条件。非定常涡格法相较于片条理论和偶极子格网法具有非常突出的优势。首先其可以考虑气动面三维效应，同时作为时域模型便于进行动力学仿真分析及导数估算，可以计算任意运动下的非定常气动力。相比于CFD方法，状态空间涡格法计算效率高，模型划分简便。

综合考虑伞翼气动载荷，绳索上的分布式定常/非定常载荷及系留翼伞对绳索的静/动力学作用，以及有效载荷舱气动力，结合飞行动力学理论表达系统动能与势能，考虑到稳定性分析及控制系统设计需求，给出气动力载荷以线化导数方式，基于Lagrange方程可建立系留翼伞刚柔耦合飞行动力学方程。

5 模拟阵风减缓控制仿真测试试验

在建立了系统开环状态空间模型、控制律环节及舵机环节后，可以得到闭环系统状态空间模型或仿真模型。在某大柔性机翼上开展模拟阵风减缓控制仿真测试试验，以验证控制方案在飞行器结构上的适用性。以离散阵风为例，选择结构某点垂向加速度作为反馈信号，将加速度计采集的信号经过低通滤波器处理后，反馈给控制器，得到舵机输入信号，指令控制舵机偏转，驱动控制面完成对飞行器结构的阵风减缓控制。

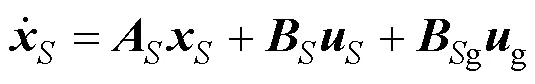
舵机环节状态空间模型为方程（18）：

控制环节传递函数为方程（19）、（20）：

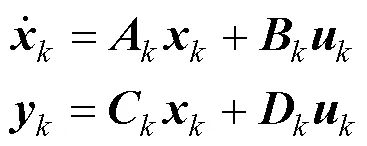
综上可得开环系统状态空间模型为方程（21）：

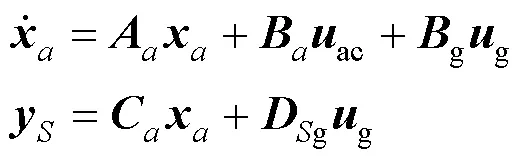
其中：

闭环系统状态空间模型为方程（22）：

根据方程（22）可以在指定控制参数的情况下，给出系统开环/闭环响应，验证控制律设计有效性。同时也可在Matlab-Simulink搭建仿真框架进行开闭环时域响应仿真，针对飞行器系统典型阵风减缓控制系统设计如图2所示。

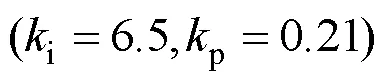
图3 风速28 m/s、阵风频率2.8 Hz阵风减缓理论仿真结果

图4 风速31 m/s、阵风频率2.8 Hz阵风减缓理论仿真结果

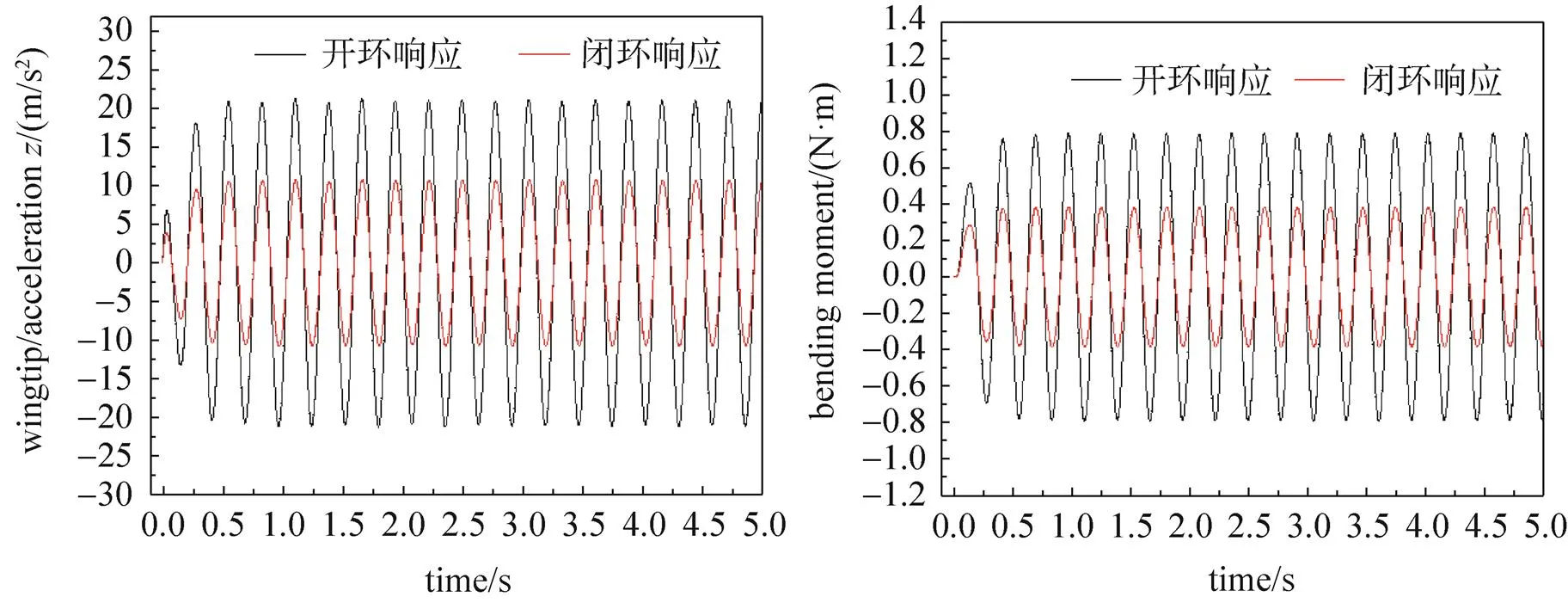
图5 风速31 m/s、阵风频率3.6 Hz阵风减缓理论仿真结果

6 结束语

刚柔混合结构建模是动力学模型建立难题之一。绳索及伞翼面都具有典型的大柔性特性，变形大，几何非线性因素突出；有效载荷舱可按具有气动外形的刚体处理。应变基有限元模型及共旋有限元模型在处理柔性绳索及膜结构等方面具有计算效率及计算精度高的优势，易与控制模型耦合。进一步考虑到翼伞飞行控制系统的设计需求，对伞翼绳索操纵作用进行建模，设计相应的传感器和具体控制方式，并对相关伺服系统进行动力学建模。考虑到控制系统的工程实施可行性，采用PID方法设计系统控制律，形成系统开、闭环控制的状态空间方程是较为有效的方法之一。在此基础上，需要进一步考虑系统的非线性因素，通过自适应PID算法，实现完整系统的工程控制，经仿真试验，验证了该方法的有效性。

[1] AKITA D. Feasibility study of a sea-anchored stratospheric balloon for long-duration flights[J]. Advanced in Space Research, 2012(50): 508–515.

[2] 梁炜, 孙青林, 贺应平, 等.复杂环境翼伞气动性能建模仿真研究[J]. 计算机仿真, 2016, 33(5): 88–64.

LIANG Wei, SUN Qinglin, HE Yingping, et al. Research on simulation of parafoil modeling of aerodynamic performance in complex environment[J]. Computer Simulation, 2016,33(5):88–64.

[3] 汪龙芳, 贺为亮. 基于索膜有限元模型的翼伞气动变形仿真[J]. 北京航空航天大学学报, 2017, 43(1): 47–52.

WANG Longfang, HE Weiliang. Parafoil aerodynamic deformation simulation based on cable-membrane finite element model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(1): 47–52.

[4] CRISFIELD MA. A consistent co-rotational formulation for non-linear, three-dimensional, beam element[J]. Computer Methods in Applied Mechanics and Engineering, 1990, 81: 131–150.

[5] 杨劲松, 夏品奇.薄壳大转动、小应变几何非线性分析共旋有限元法[J]. 中国科学: 技术科学, 2012, 42(11): 1295–1304.

YANG Jinsong, XIA Pinqi. Finite element corotational formulation for geometric nonlinear analysis of thin shells with large rotation and small strain[J]. SCIENTIA SINICA Technologica, 2012, 42(11): 1295–1304.

[6] NOUR-OMID B, RANKIN CC. Finite rotation analysis and consistent linearization using projectors[J]. Computer Methods in Applied Mechanics and Engineering, 1991,93: 353–384.

[7] 刘燚. 大柔性飞机气动弹性稳定性及动响应分析[D]. 北京: 北京航空航天大学, 2016.

[8] 王立波. 考虑气动弹性效应的飞机飞行动力学研究[D]. 北京: 北京航空航天大学, 2013.

[9] WASZAK MR, SCHMIDT DK. Flight dynamics of aeroelastic vehicles[J]. Journal of Aircraft, 1988, 25(6): 563–571.

[10] 谢长川. 飞行器气动弹性稳定性静/动耦合理论与试验研究[D]. 北京: 北京航空航天大学, 2011.

[11] PAI PF. Highly flexible structures: modeling, computation, and experimentation[M]. Reston, VA, USA: AIAA Inc, 2007.

[12] ROEMO G, FRULLA G, CESTINO E, et al. Nonlinear aeroelastic modeling and experiments of flexible wings[C]// 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, Rhode Island, 2006: AIAA-2006-2186.

[13] 钱翼稷. 空气动力学[M]. 北京: 北京航空航天大学出版社, 2004.

[14] WERTER N P M, BREUKER DE R, ABDALLA M M. Continuous-time state-space unsteady aerodynamic modeling for efficient loads analysis[J]. AIAA Journal, 2018, 56(3): 905–916.

[15] MARANIELLO S, PALACIOS R. State space realisation and model reduction of potential-flow aerodynamics for HAWT applications[J]. Journal of Physics: Conference Series. 2018, 1037(2): 022033,

[16] JOSEPH K, ALLEN P. Low-speed aerodynamics[M]. Cambridgeshire: Cambridge University Press, Second Edition, 2001.

[17] 刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2016.

[18] BI Y, XIE C, AN C. et al. Gust load alleviation wind tunnel tests of a large-aspect-ratio flexible wing with piezoelectric control[J]. Chinese Journal of Aeronautics, 2017, 30(1): 292–309.

[19] CHEN PC, LIU DD, KARPEL M. ZAERO theoretical manual version 8.2[M]. ZONA Technology Inc., 2008.

[20] TIFFANY SH, KARPEL M. Aeroservoelastic modeling and application using minimumstate approximations of the unsteady aerodynamics[R]. Reston: AIAA, 1989: AIAA-89-1188.

Research on rigid flexible hybrid model control method for tethered parafoil

LIU Songlin1, AN Chao2, ZHU Jing3, XIE Changchuan2, XU Ping2

(1. Shenzhen Baichuan Rongchuang Technology Co., LTD., Shenzhen 518110, China; 2. Beihang University, Beijing 100191, China;3. 91977 Army, Beijing 102299, China)

The tethered parachute can stay in the air for a long time with the load of wind, which has the advantages of strong wind resistance, high load weight, low power consumption and long reconnaissance range compared with the tethered UAVs. Due to the rigid-flexible coupling characteristics of the tethered parachute, the control system is difficult to design, and there is a lack of effective control models and immature technology, which restricts the application of this new hysteretic flight platform. In this paper, the tethered parachute control method based on the rigid-flexible coupling dynamics modeling, the unsteady aerodynamic modeling of tethered parachute, the rigid-flexible coupling state-space modeling of tethered parachute and the tethered parachute rigid-flexible hybrid control technology implementation are introduced, and the effectiveness of the method is verified.

Tethered parachute; Rigid flexible coupling; Coupling control; Simulation test

V212

A

CN11-1780(2022)09-0022-08

10.12347/j.ycyk.20220706001

刘松林, 安朝, 朱靖, 等.系留翼伞刚柔混合模型控制方法探索研究[J]. 遥测遥控, 2022, 43(5): 22–29.

DOI：10.12347/j.ycyk.20220706001

: LIU Songlin, AN Chao, ZHU Jing, et al. Research on rigid flexible hybrid model control method for tethered parafoil[J]. Journal of Telemetry, Tracking and Command, 2022, 43(5): 22–29.

基金项目：国防创新专项（1816318LZ00400101）；深圳市百川融创科技有限公司拖曳伞监视系统

2022-07-06

刘松林 1974生生，博士，研究员，主要研究方向为航天航空系统工程。

安 朝 1991年生，博士，副教授，主要研究方向为气动弹性力学。

朱 靖 1974年生，博士，研究员，主要研究方向为模式识别与智能系统。

谢长川 1976年生，博士，副教授，主要研究方向为气动弹性力学、飞行动力学与控制。

徐 萍 1978年生，博士，讲师，主要研究方向为可靠性与系统工程。

(本文编辑：潘三英)