基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识

李 婕 杨淑英 谢 震 张 兴

基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识

李 婕 杨淑英 谢 震 张 兴

（合肥工业大学电气与自动化工程学院 合肥 230009）

为解决采用粒子群优化算法（PSO）辨识永磁同步电机（PMSM）参数存在的计算量大、运行时间长的问题，提出一种基于有效信息迭代的快速粒子群优化算法（FPSO），该算法在最大转矩电流比（MTPA）控制策略下在线对永磁同步电机参数进行快速辨识。基于动态电压方程构建新的适应度函数，并通过迭代有效电机参数信息和增添新的迭代终止条件改进标准粒子群优化算法（SPSO）的收敛快速性。为了克服电压估算误差对辨识精度的影响，在非线性补偿算法的基础上，讨论一种剔除电流过零一定范围内数据的预处理方案。实验结果表明，在不影响系统正常运行的情况下，实现了对永磁同步电机的交、直轴电感和永磁体磁链的快速辨识，且辨识结果具有较高的精度。

永磁同步电机 参数辨识 粒子群优化算法 数据预处理

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因其自身在效率、功率密度等诸多方面的优势而被广泛应用于机器人、工业伺服系统、新能源电动汽车等领域[1]。电机控制性能对交、直轴电感、永磁体磁链等参数有着较强的依赖性，但受到磁饱和程度、温度等影响，参数量值在系统运行过程中会出现较大的变化[2]。研究永磁同步电机参数在线辨识对控制系统运行性能有着重要的现实意义。

为了实现永磁同步电机的参数在线辨识，需要解决方程组欠秩、逆变器非线性影响和辨识算法设计等问题，这也是永磁同步电机参数辨识策略研究的焦点问题。

对于方程组欠秩的研究，主要通过减少待辨识参数的个数或增加方程组中约束方程的个数来解决。文献[3]依据最大转矩电流比（Maximum Torque Per Ampere, MTPA）轨迹跟踪控制的需求，只对交轴电感和永磁体磁链两个参数进行在线辨识。文献[4]通过实验测试建立了定子电阻与永磁体磁链关于温度和交、直轴电流的数学模型，在参数在线辨识过程中，先利用获取的相关信息估算出定子电阻与永磁体磁链，再将其应用到定子电压方程对交、直轴电感进行辨识。该方案的辨识精度受所建立数学模型的精度影响，且需要检测电机温度。文献[5]通过分析参数变化的特点将电磁参数分为快变参数和慢变参数两组，然后按时间尺度分步辨识，两组辨识结果相互更新。文献[6]基于在特定电压矢量下的三相定子电压方程，经变换建立了仅包含可知量和待辨识参数的目标函数，通过测量逆变器直流母线电压和三相定子电流导数，实现对交、直轴电感的辨识。该方案辨识速度快，但对系统硬件的要求较高。文献[7]在d=0的矢量控制策略下，通过向d轴注入负序电流得到两组不同运行工况下的稳态电压方程，实现了约束方程数的增加。为保证辨识的精度，注入的扰动电流需足够大，这会造成系统转矩脉动。文献[8]同样是在d=0的矢量控制策略下，通过向转子位置信号中交替注入正、负扰动量，获取两种转子位置偏置下的稳态电压方程，建立与定子电阻及交、直轴电感无关的适应度函数，实现对永磁体磁链的辨识。

对于逆变器非线性影响，可以通过检测电路直接对定子电压进行检测[9]；也可以设计相应的补偿算法提升电压估算精度[10-12]。前者不仅需要增加额外的检测电路，且精度会受到低通滤波器特性的影响；后者补偿精度有限，且补偿效果会受到系统运行状态的影响。

对于辨识算法设计问题，目前常用的辨识算法有递推最小二乘法、扩展卡尔曼滤波器法、模型参考自适应法、神经网络法、群智能算法等。递推最小二乘法原理简单、易于实现，但抗干扰能力较差；扩展卡尔曼滤波器法虽对外部噪声干扰有较强的抑制能力，但当待辨识参数较多时，算法的运算量较大；模型参考自适应法的核心在于自适应律，通常采用李雅普诺夫稳定理论和Popov超稳定理论进行设计，能够保证待辨识参数的收敛性，但多参数辨识时，自适应律的设计难度较大，且对模型精度的依赖性较强。以上三种算法均常用于线性系统，对于非线性系统，需先转化为线性系统，这会在一定程度上影响参数辨识的结果。相比之下，人工智能算法和群智能算法的应用更加广泛且更加灵活简便。神经网络通常需要进行离线训练，具有更高的智能性，其辨识结果对先验值有一定的依赖性；遗传算法和粒子群优化（Particle Swarm Optimization, PSO）算法是较为常用的两种群智能算法，遗传算法适合数字实现，粒子群优化算法收敛速度快。在诸如新能源汽车、主轴伺服系统等应用场合，电机转速变化范围大，且变化速度快，这对参数辨识算法的快速性提出了需求。在此应用场合下，PSO算法有着较好的适应性。

PSO算法因设计简单、可移植性好、搜索精度较高且收敛速度相对较快等优点被广泛应用于各领域，但在实际应用中PSO算法同时存在易陷入局部最优、计算量大、运行时间长等缺点。为使PSO算法能更好地运用于PMSM参数辨识中，系列改进PSO算法被相继提出。文献[13]提出了由所有粒子个体最好位置的平均值定义的平均最好位置和依据柯西分布的密度函数得到的柯西变异策略相结合的柯西变异粒子群算法，对表贴式永磁同步电机的电磁参数进行了辨识。文献[14]提出了将粒子群划分为多个子种群，并以一定的通信频率交换有用信息的协同粒子群算法，对表贴式永磁同步电机的电磁参数和机械参数进行了辨识。文献[15]提出了先利用PSO算法优化算法的初始参数，再与小生镜策略和混沌变异策略相结合的初始参数优化的混沌变异小生镜粒子群优化算法，同时辨识了PMSM的定子电阻、交、直轴电感、永磁体磁链及转动惯量5个参数。这些改进方案通过增强种群多样性，在不同程度上改善了PSO算法的全局搜索能力和跳出局部最优的能力，提高了寻优的准确性。

针对PMSM运行特点和实际应用中对辨识快速性的需求，本文提出一种基于有效信息迭代的快速粒子群优化（Fast Particle Swarm Optimization, FPSO）算法，该算法在MTPA控制策略下在线对PMSM参数进行快速辨识。一方面基于离散的动态电压方程建立了新的适应度函数，以降低算法所需搜索目标的难度；另一方面在标准粒子群优化（Stand Particle Swarm Optimization, SPSO）算法的基础上，引入前一次电机参数辨识的结果，即PMSM有效参数信息，为种群的寻优提供导向作用，以提高算法的收敛速度。同时，增添新的迭代终止条件，以减少算法的运行时长。本文在采集辨识所需的数据后，对其进行预处理，剔除过零点附近一定范围内的数据，克服死区补偿误差影响，提高参数辨识的精度。最后，通过仿真和实验验证了所提方案的有效性和可行性。

1 PSO算法

PSO算法是心理学专家J. Kennedy和计算机研究学者R. Eberhart于1995年共同提出的一种群智能算法[16]。PSO算法受启发于鸟群的觅食行为，利用群体中个体间相互的信息交流，通过不断的竞争与合作实现迭代优化。PSO算法中的每个粒子都只包含自身速度和位置信息，在每次迭代过程中，算法通过速度和位置更新规律对粒子个体信息进行更新。SPSO算法的粒子信息更新规律可用公式描述为

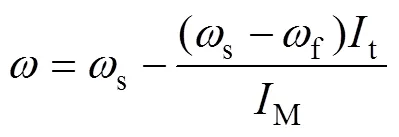
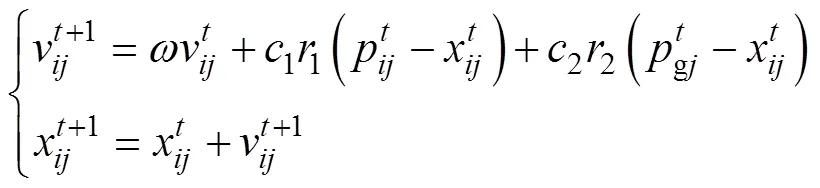
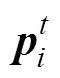
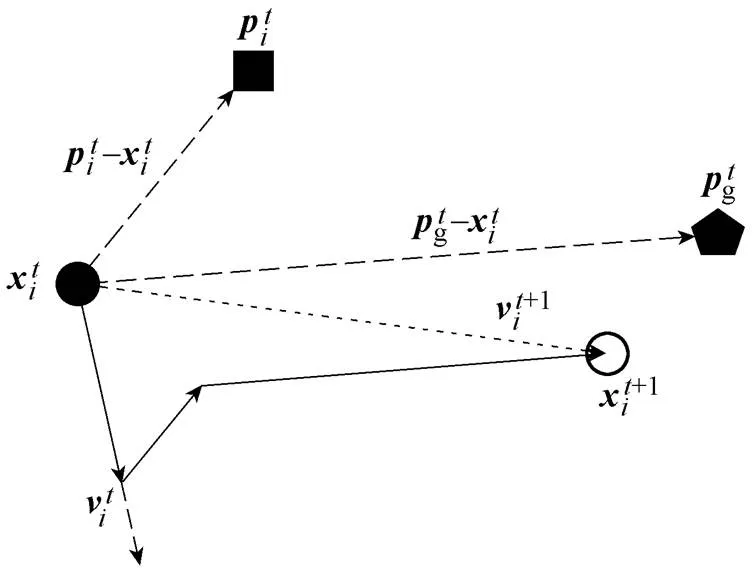
图1 粒子移动示意图

2 PMSM参数在线辨识策略

2.1 适应度函数

基于PSO算法在线辨识PMSM参数的基本思想是将参数辨识问题转化为极值优化问题[13-15]。在电机实体与可调模型具有相同输入的条件下，依据二者输出的差值，不断修正可调模型中待估计参数值，从而使其收敛到电机实际参数值，实现对参数的辨识。

PMSM在dq旋转坐标系下的定子电压方程可表示为

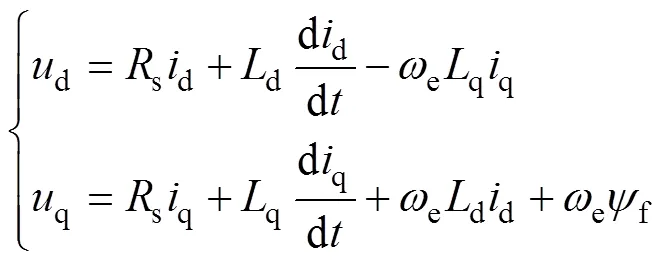
本文将动态电压方程作为可调模型，在数字实现过程中，对式（3）进行离散化，得

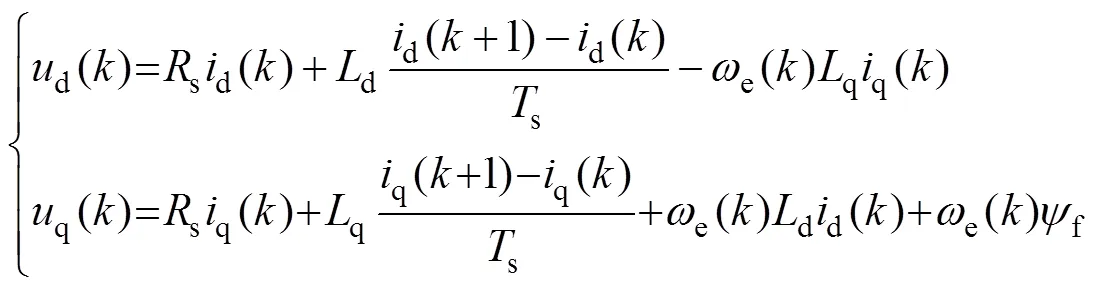
因MTPA控制策略工作点的计算与定子电阻值无关且定子电阻值对系统整体控制效果的影响较小，故本文仅对PMSM的交、直轴电感和永磁体磁链进行在线辨识。消去离散动态电压方程中的定子电阻，得

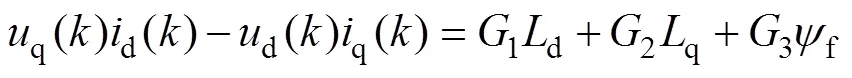
其中

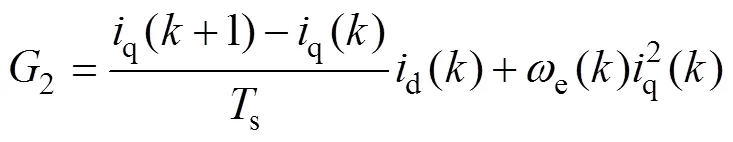
将d、q轴定子电流和转子电角速度视为电机参数辨识系统的输入信号，式（5）等号左边视为输出信号，可建立适应度函数为

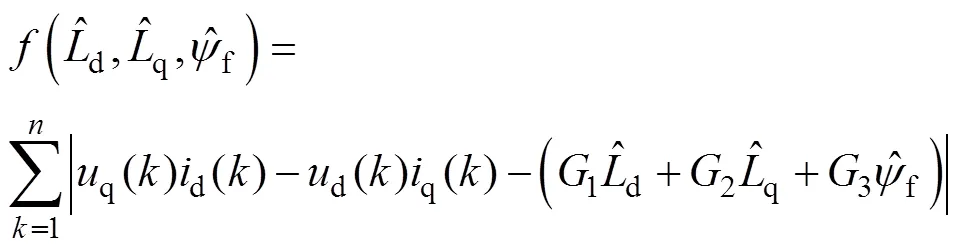
2.2 数据预处理

考虑到逆变器非线性因素的影响，在由电压指令估算定子电压时，需要进行补偿，比较典型的补偿方案[10]为

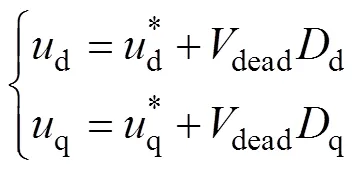
其中

图2记录了参数辨识过程中，逆变器非线性因素所带来的影响。图2a为电机三相定子电流，图2b为电机d、q轴电流，图2c为对应图2b所示电流波形由电机自身和可调模型所获得的d、q轴电压以及计算获得的参数辨识系统输出信号值，可调模型电压包含了式（7）所示的死区补偿算法。由图2a中可以看出，由于死区的存在，出现了明显的零电流钳位现象，使得电机电流过零点附近的实际电压与可调模型的计算结果存在明显偏差。为避免电压偏差对参数辨识精度的影响，将在三相定子电流过零点附近15°采集的数据剔除，不再参与辨识过程。图2d就是将图2c中的数据经预处理后得到的波形。

2.3 快速粒子群优化算法

PSO算法自被提出以来就受到了国内外学者的广泛关注。迄今为止，PSO算法的改进方案从简单的参数选取到复杂的速度、位置更新方式有着众多研究成果[17-20]。对于上述建立的适应度函数，简单的SPSO算法理论上便可以达到寻优的目的，但大量的数据使得算法的运行时长增加，影响了辨识的快速性。而一些实际应用场景对算法的快速性有着更高的需求，故本文结合PMSM运行特点，对算法寻优的快速性进行了改进，提出了一种基于有效信息迭代的快速粒子群优化算法，以期提升PMSM参数在线辨识的实时性。

文献[14]为增强PSO算法的多样性提出了基于协同策略的协同粒子群优化（Collaborative Particle Swarm Optimization, CPSO）算法，但明显损害了算法的快速性。故在运用CPSO算法对PMSM参数进行辨识时，认为通常情况下，实际PMSM参数的变化并不会非常剧烈，相邻两次参数辨识结果相近。则将前一次参数辨识的结果初始化为其中一个种群的一个粒子，用以提高CPSO算法寻优的快速性。借鉴这一思想，本文将前一次参数辨识的结果作为FPSO算法下一次参数辨识的已知有效真实参数信息，为粒子群的寻优提供导向作用，加快种群的收敛速度。

为使受到有效参数信息影响的粒子能较为快速地移动到前一次参数辨识结果附近，采用单导向学习机制来避免“振荡”现象的发生。此时粒子的移动方向和步长将由粒子自身先前的移动方向和其与前一次参数辨识结果的位置关系决定。此粒子信息更新规律可描述为

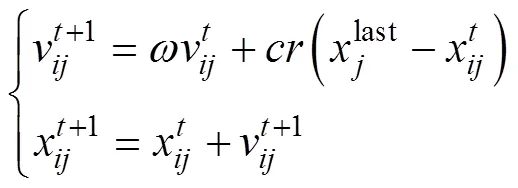
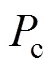
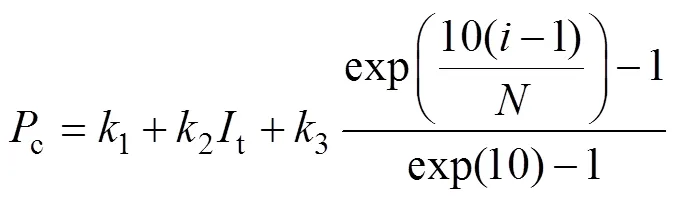
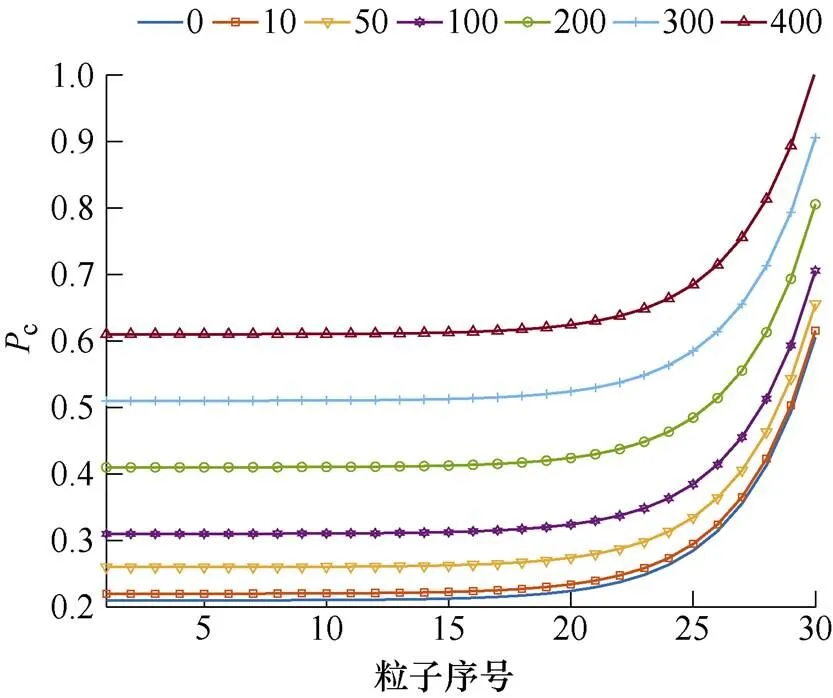
图3 粒子的值

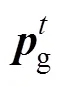
3 实验验证

为验证上述PMSM参数在线辨识策略的辨识效果，设计了如图5所示的半实物仿真实验平台，对应的PMSM控制框图如图6所示。PMSM模型在实时仿真器RT Box中运行，控制算法及参数辨识算法在DSP TMS320F28379中运行。PMSM模型参数见表1。PWM开关频率为10kHz，ADC采样频率为20kHz。

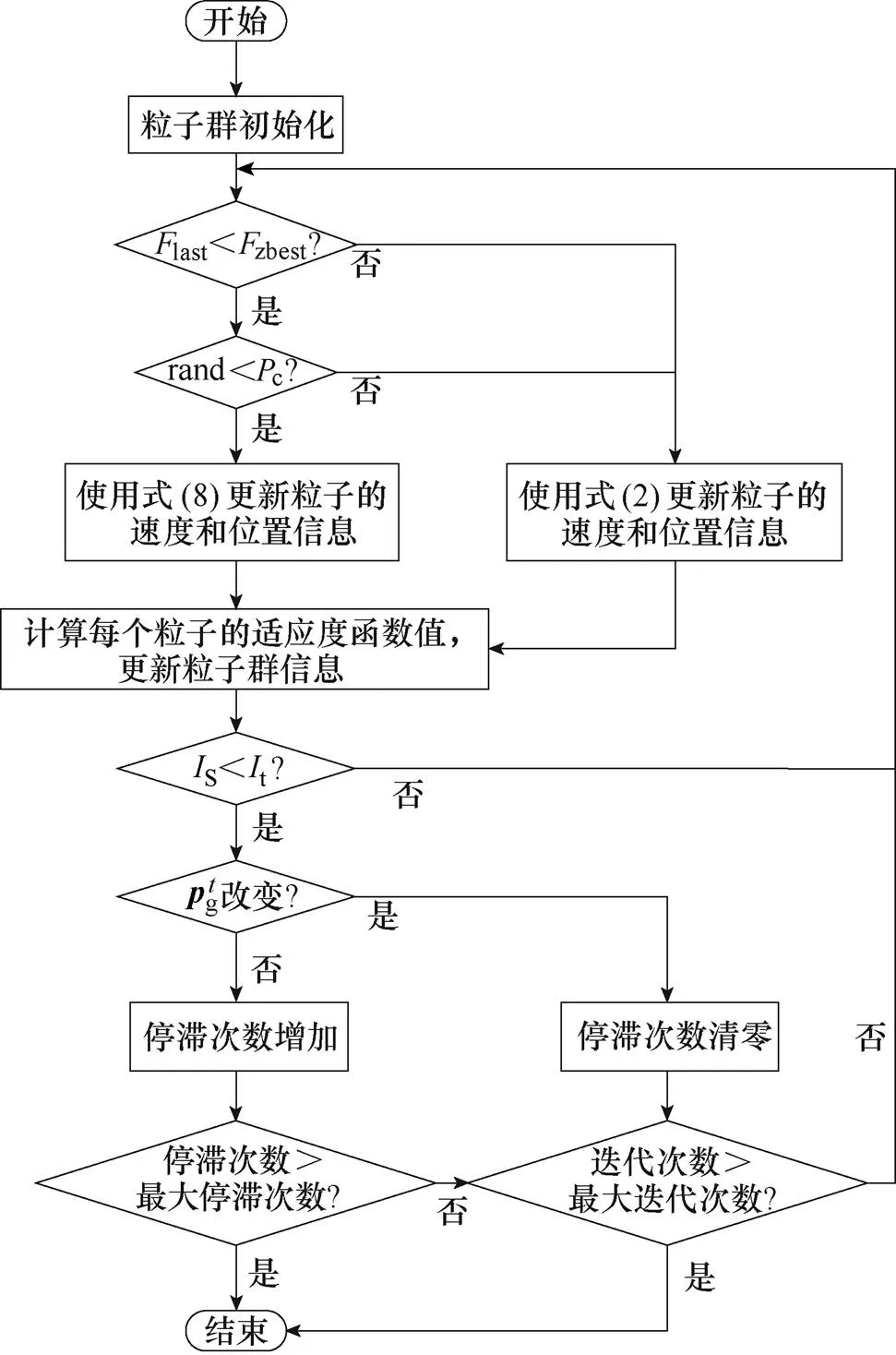
图4 FPSO算法流程

图5 实验平台

图7为在电磁转矩为15N∙m，转速为960r/min和360r/min的工况下，SPSO算法在使用数据预处理前后对PMSM的d、q轴电感和永磁体磁链单次辨识的结果。从图中可以看出，使用经过预处理的数据，降低了电压估算误差的影响，使得辨识结果的精度得到提升。

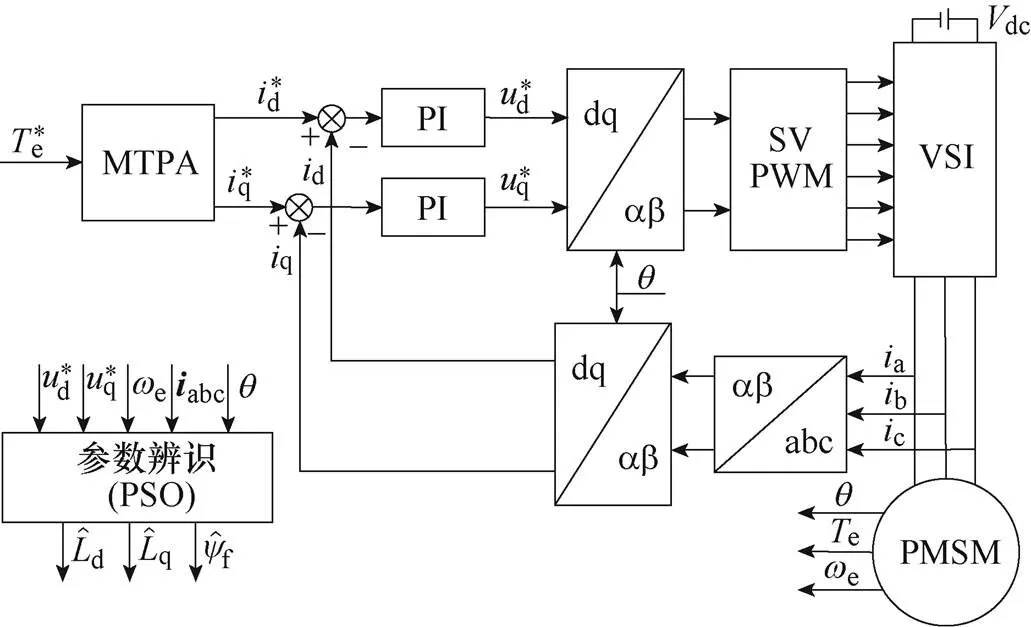
图6 系统控制框图

表1 永磁同步电机参数

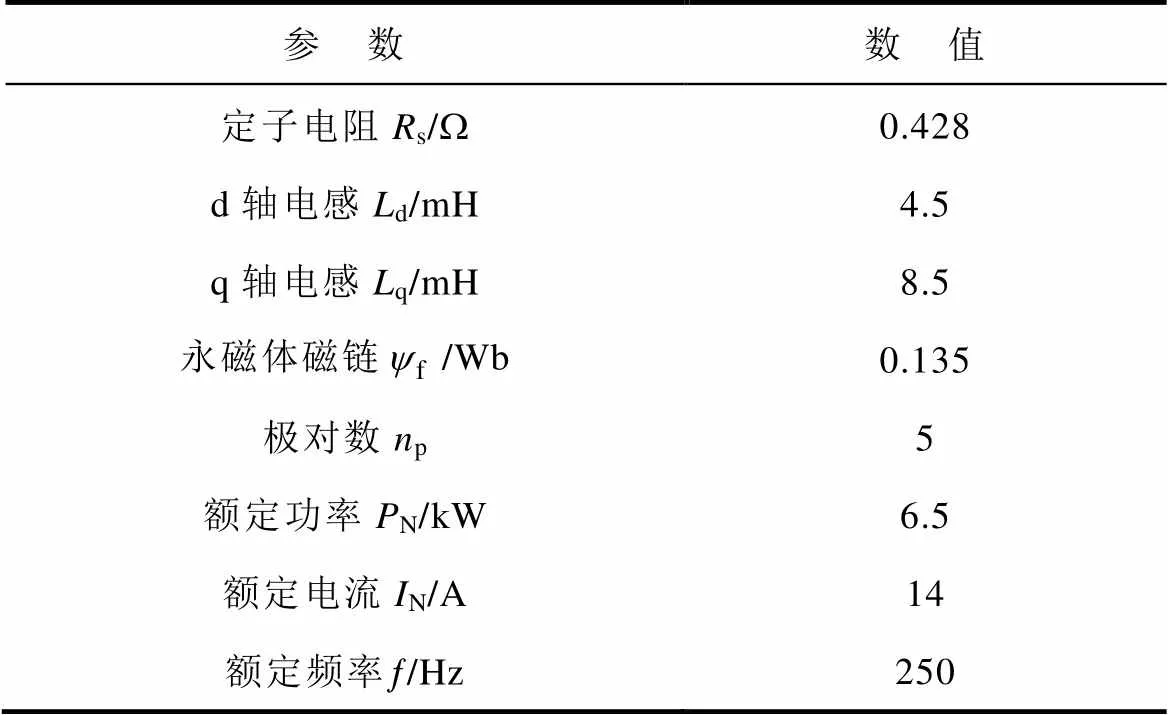
Tab.1 Parameters of the PMSM

图8为在与图7相同的工况下，SPSO算法和FPSO算法分别使用同一组采集并经过预处理后的数据对PMSM的d、q轴电感和永磁体磁链单次辨识的结果。因FPSO算法中引入前一次参数辨识结果为粒子种群寻优提供导向作用，并增添最大停滞次数作为迭代终止条件，使得算法更加多样、合理，故相较于SPSO算法，FPSO算法在保证辨识结果准确性的情况下，具有更快的收敛速度，更少的迭代次数。

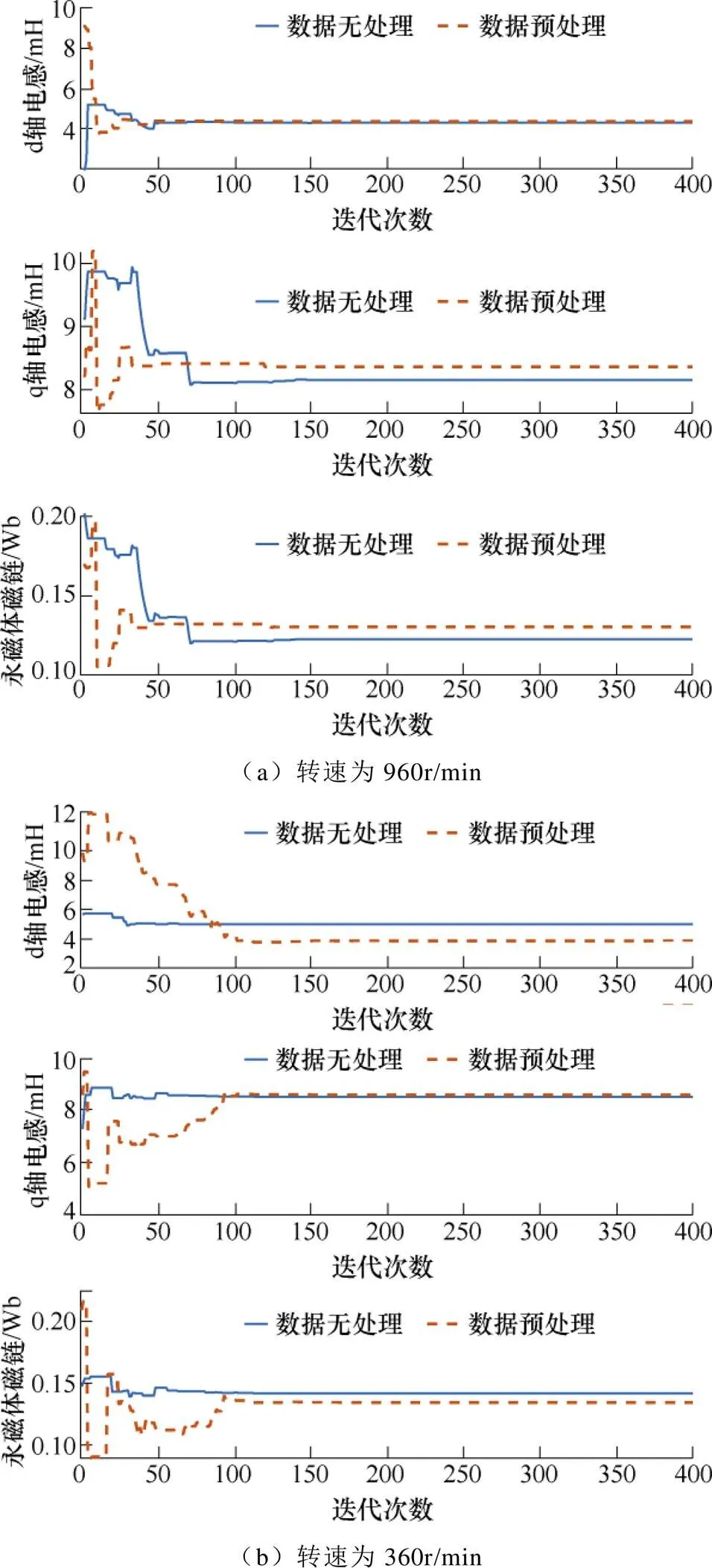
图7 数据预处理对参数辨识结果的影响

图9为在电磁转矩为15N∙m，转速为960r/min的工况下，选取不同值时，对PMSM的d、q轴电感和永磁体磁链连续辨识的波形。从图中可以看出，越大，辨识结果的稳定性和准确性越高。这是因为在实际应用场合，采样器精度、内外部环境扰动和数字延迟等因素会导致采集的数据产生不同程度的偏差，所以当用于辨识的数据量较少时，辨识的结果易受到影响，而增大数据量则能够在一定程度上降低这种不利影响，提高辨识的稳定性和准确性。同时，越大，程序的运行时间会越长，故在实际应用中，应根据需求合理选取数据量。

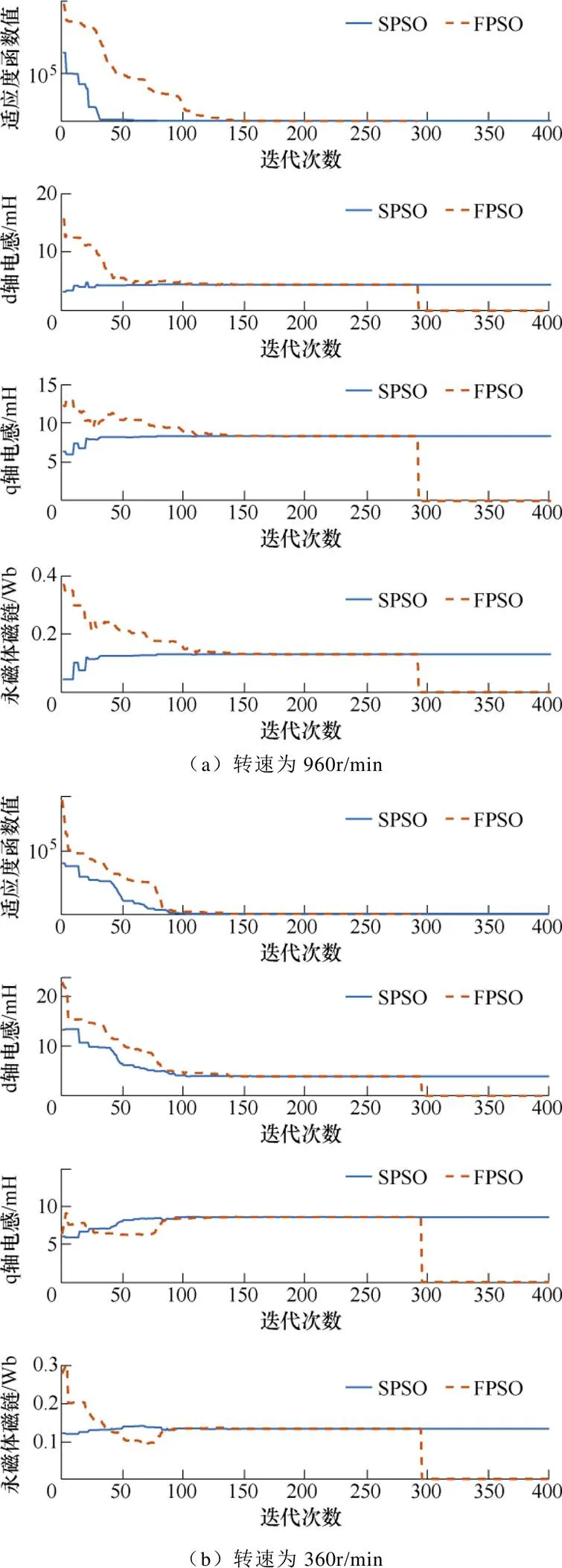
图8 FPSO算法对参数辨识结果的影响

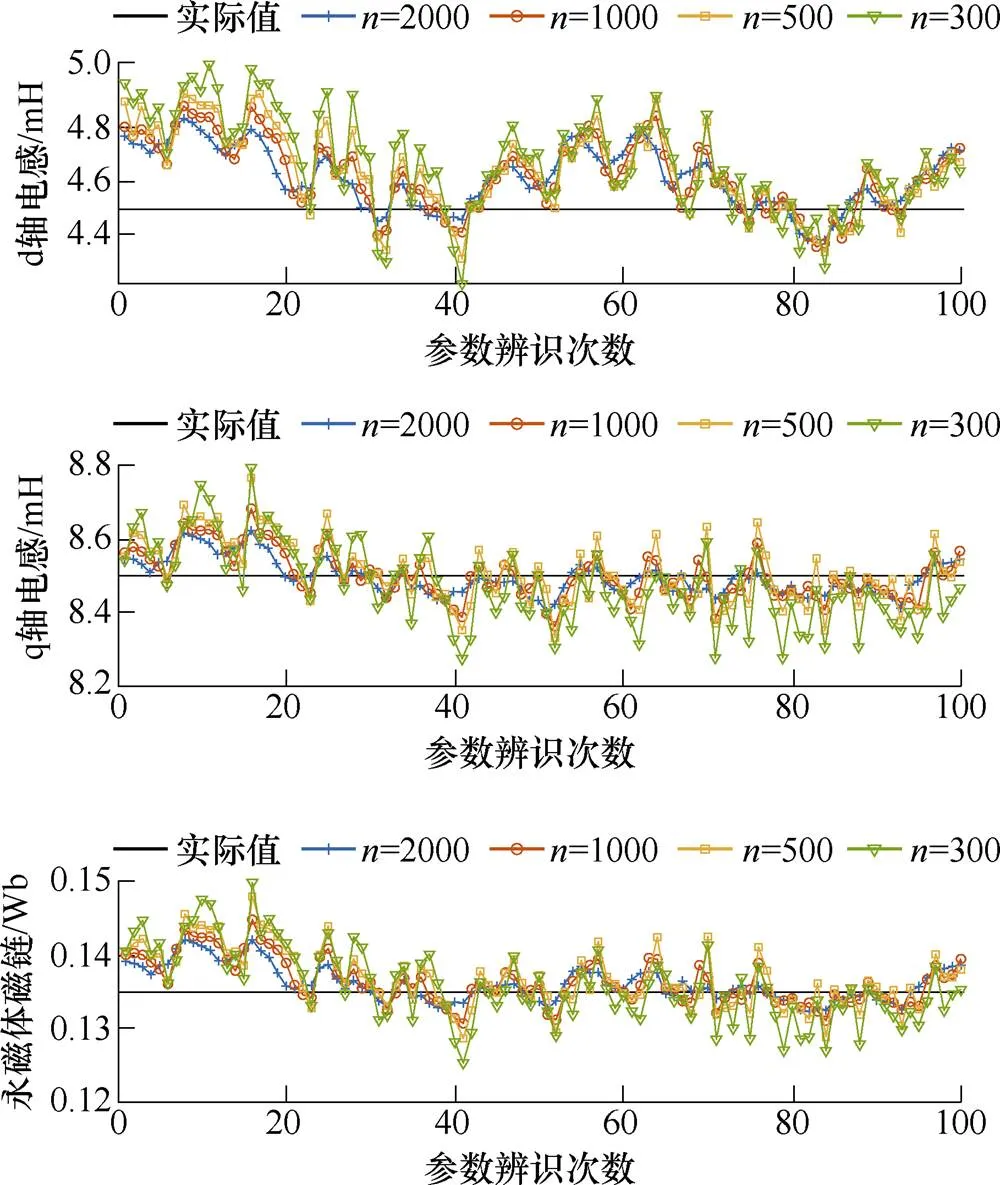
图9 稳态时PMSM参数辨识波形

上述实验中，在电磁转矩为15N∙m，转速为960r/min的工况下，DSP的主频配置为100MHz，设置为1 000时，SPSO算法在使用没有经过预处理的数据进行单次辨识时，因为SPSO算法每次辨识过程固定迭代400次，所以完成一次参数辨识DSP的运行时间约为20s。而SPSO算法在使用经过预处理的数据进行单次辨识时，因为剔除了电流过零15°范围内的数据，所以DSP的运行时间约为16s。FPSO算法在使用经过预处理的数据进行单次辨识时，因为FPSO算法辨识过程的迭代次数不是固定的，所以每次辨识DSP的运行时间会略有不同，平均约为9.5s。而所提策略时间约占完成一次参数辨识时间的3/5。可以明显看出，本文提出的PMSM参数在线辨识策略显著减少了DSP的运行时长。

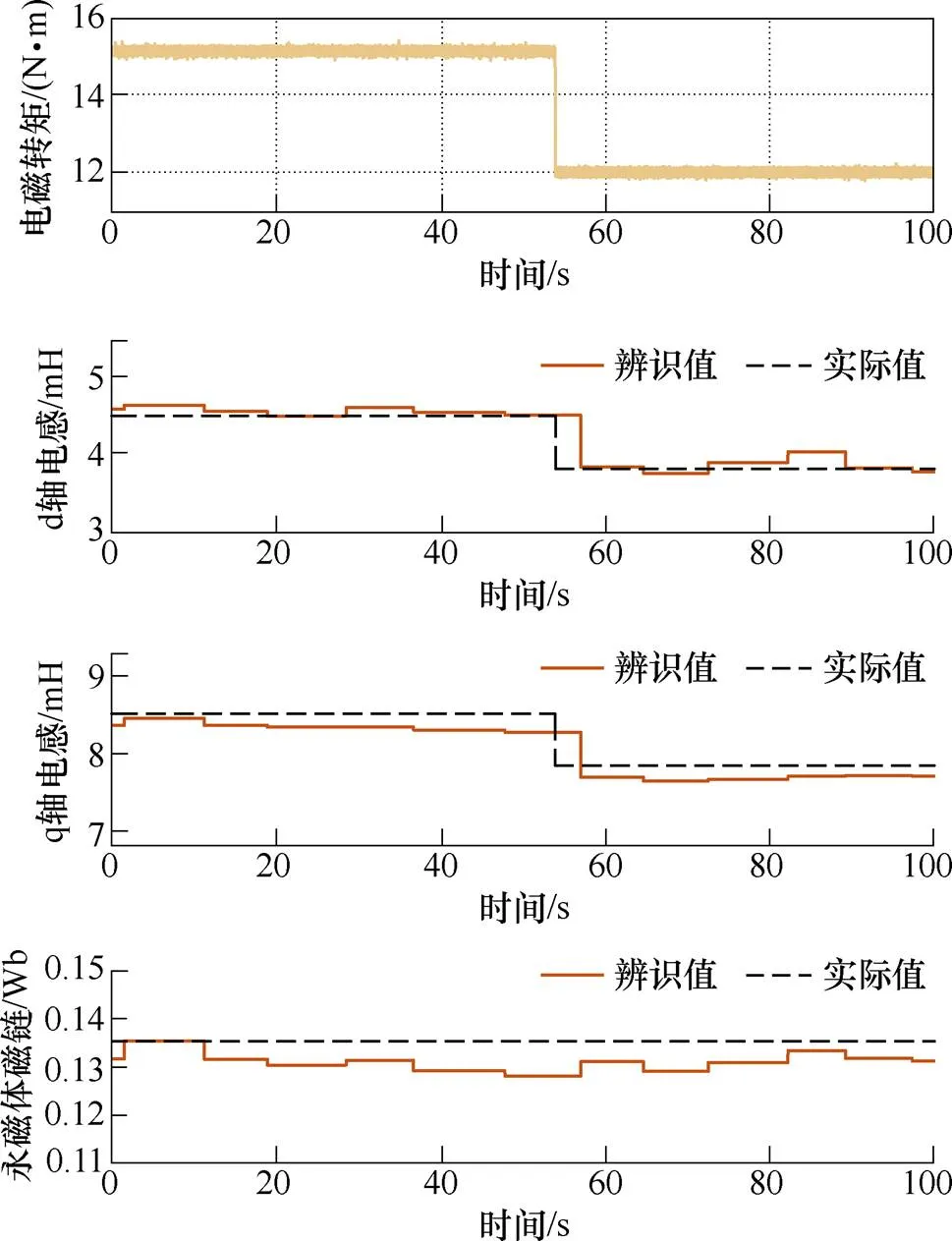
图10 电磁转矩突变时PMSM参数辨识波形

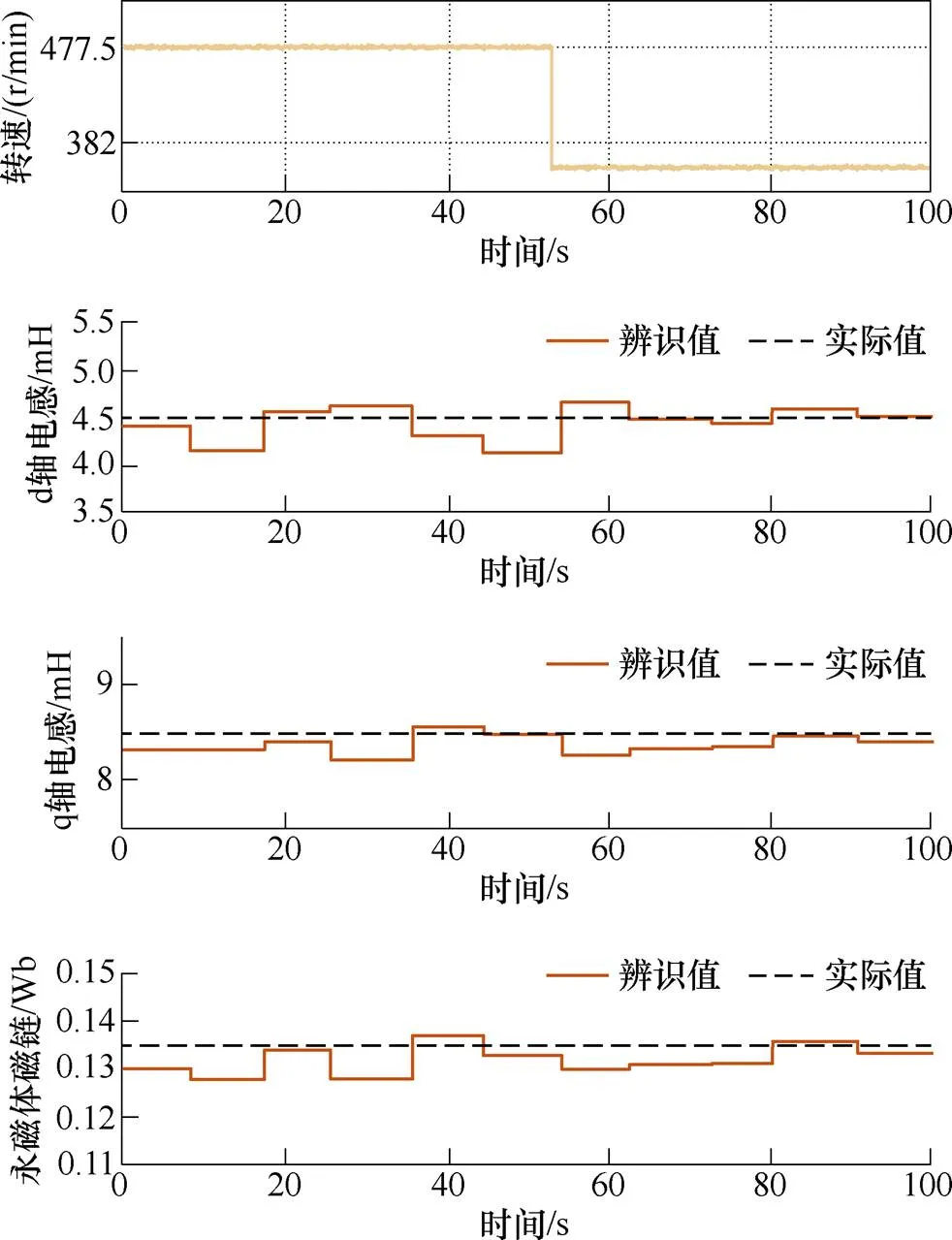
图11 转速突变时PMSM参数辨识波形

4 结论

本文提出了一种基于有效信息迭代的快速粒子群优化算法。在SPSO算法基础上，通过迭代有效电机参数信息和增添新的迭代终止条件改善了算法的收敛快速性。在MTPA控制策略下，建立了基于离散动态电压方程的新适应度函数。在电压估算上，运用系统采集并经过非线性补偿，且剔除电流过零一定范围内采样后的数据。FPSO算法实现了对PMSM交、直轴电感和永磁体磁链的在线辨识。实验结果表明，在不影响系统正常运行的情况下，该策略能够较为准确地辨识出电机的电磁参数，同时有效地减少了算法的运行时长，降低了系统的计算负担。

[1] 夏长亮, 王东, 程明, 等. 高效能电机系统可靠运与智能控制基础研究进展[J]. 中国基础科学, 2017, 19(1): 16-23.

Xia Changliang, Wang Dong, Cheng Ming, et al. Advancements of basic researches on high-efficiency motor systems reliability and intelligence control[J]. China Basic Science, 2017, 19(1): 16-23.

[2] Underwood S J, Husain I. Online parameter esti- mation and adaptive control of permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2435-2443.

[3] 金宁治, 周凯, Herbert Ho-Ching IU. 带有自适应参数辨识的IPMSM MTPA控制[J]. 电机与控制学报, 2020, 24(7): 90-101.

Jin Ningzhi, Zhou Kai, Herbert Ho-Ching IU. Model reference adaptive identification based MTPA control method for interior PM synchronous motor[J]. Electric Machines and Control, 2020, 24(7): 90-101.

[4] 连传强, 肖飞, 高山, 等. 基于实验标定及双时间尺度随机逼近理论的内置式永磁同步电机参数辨识[J].中国电机工程学报, 2019, 39(16): 4892-4898, 4991.

Lian Chuanqiang, Xiao Fei, Gao Shan, et al. Parameter identification for interior permanent magnet synchronous motor based on experimental calibration and stochastic approximation theory with two time scales[J]. Proceedings of the CSEE, 2019, 39(16): 4892-4898, 4991.

[5] Dang Dongquang, Rafaq M S, Choi H H, et al. Online parameter estimation technique for adaptive control applications of interior PM synchronous motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1438-1449.

[6] Bui M X, Faz Rahman M, Guan Deqi, et al. A new and fast method for on-line estimation of d and q axes inductances of interior permanent magnet synchronous machines using measurements of current derivatives and inverter DC-bus voltage[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7488-7497.

[7] Liu Kan, Zhang Qiao, Chen Jintao, et al. Online multiparameter estimation of nonsalient-pole PM synchronous machines with temperature variation tracking[J]. IEEE Transactions on Industrial Elec- tronics, 2011, 58(5): 1776-1788.

[8] Liu Kan, Zhu Ziqiang. Position-offset-based parameter estimation using the adaline NN for condition moni- toring of permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2372-2383.

[9] 吴春, 赵宇纬, 孙明轩. 采用测量电压的永磁同步电机多参数在线辨识[J]. 中国电机工程学报, 2020, 40(13): 4329-4339.

Wu Chun, Zhao Yuwei, Sun Mingxuan. Multiparameter online identification for permanent magnet syn- chronous machines using voltage measurements[J]. Proceedings of the CSEE, 2020, 40(13): 4329-4339.

[10] Wang Yuanlin, Xie Wei, Wang Xiaocan, et al. A precise voltage distortion compensation strategy for voltage source inverters[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 59-66.

[11] 史婷娜, 刘华, 陈炜, 等. 考虑逆变器非线性因素的表贴式永磁同步电机参数辨识[J]. 电工技术学报, 2017, 32(7): 77-83.

Shi Tingna, Liu Hua, Chen Wei, et al. Parameter identification of surface permanent magnet syn- chronous machines considering voltage-source inverter nonlinearity[J]. Transactions of China Electro- technical Society, 2017, 32(7): 77-83.

[12] 陈斌, 王婷, 吕征宇, 等. 电压型逆变器非线性的分析及补偿[J]. 电工技术学报, 2014, 29(6): 24-30.

Chen Bin, Wang Ting, Lü Zhengyu, et al. The analysis and compensation of voltage source inverter nonlinearity[J]. Transactions of China Electro- technical Society, 2014, 29(6): 24-30.

[13] 傅小利, 顾红兵, 陈国呈, 等. 基于柯西变异粒子群算法的永磁同步电机参数辨识[J]. 电工技术学报, 2014, 29(5): 127-131.

Fu Xiaoli, Gu Hongbing, Chen Guocheng, et al. Permanent magnet synchronous motors parameters identification based on cauchy mutation particle swarm optimization[J]. Transactions of China Elec- trotechnical Society, 2014, 29(5): 127-131.

[14] 程善美, 张益. 基于协同粒子群算法的PMSM在线参数辨识[J]. 电气传动, 2012, 42(11): 3-6.

Cheng Shanmei, Zhang Yi. Collaborative particle swarm optimization based online parameter identi- fication applied to PMSM[J]. Electric Drive, 2012, 42(11): 3-6.

[15] 刘细平, 胡卫平, 丁卫中, 等. 永磁同步电机多参数辨识方法研究[J]. 电工技术学报, 2020, 35(6): 1198-1207.

Liu Xiping, Hu Weiping, Ding Weizhong, et al. Research on multi-parameter identification method of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(6): 1198-1207.

[16] Kennedy J, Eberhart R. Particle swarm optimi- zation[C]//ICNN'95-International Conference on Neural Networks, Australia, 1995: 1942-1948.

[17] Xu Guiping, Cui Quanlong, Shi Xiaohu, et al. Particle swarm optimization based on dimensional learning strategy[J]. Swarm and Evolutionary Computation, 2019, 45: 33-51.

[18] Cao Yulian, Zhang Han, Li Wenfeng, et al. Com- prehensive learning particle swarm optimization algorithm with local search for multimodal fun- ctions[J]. IEEE Transactions on Evolutionary Com- putation, 2019, 23(4): 718-731.

[19] 刘朝华, 李小花, 周少武, 等. 面向永磁同步电机参数辨识的免疫完全学习型粒子群算法[J]. 电工技术学报, 2014, 29(5): 118-126.

Liu Zhaohua, Li Xiaohua, Zhou Shaowu, et al. Comprehensive learning particle swarm optimization algorithm based on immune mechanism for permanent magnet synchronous motor parameter identification[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 118-126.

[20] 周建萍, 李欣煜, 茅大钧, 等. 基于改进PSO算法的非理想电压条件下电力弹簧控制策略[J]. 电力系统自动化, 2018, 42(22): 165-171.

Zhou Jianping, Li Xinyu, Mao Dajun, et al. Control strategy of electric spring under non-ideal voltage conditions based on improved PSO algorithm[J]. Automation of Electric Power Systems, 2018, 42(22): 165-171.

Online Parameter Identification of Permanent Magnet Synchronous Motor Based on Fast Particle Swarm Optimization Algorithm with Effective Information Iterated

（College of Electrical Engineering and Automation Hefei University of Technology Hefei 230009 China）

In order to solve the problem of large computation and long running time in the parameter identification of permanent magnet synchronous motor (PMSM) by particle swarm optimization algorithm (PSO), a fast particle swarm optimization algorithm (FPSO) is proposed by introducing the effective parameter information into the present searching process. The proposed FPSO algorithm can quickly identify the parameters of the PMSM under the maximum torque per ampere (MTPA) operation online. A new fitness function was constructed based on the dynamic voltage equations, and the converging performance of the stand particle swarm optimization algorithm (SPSO) was improved by introducing an effective motor parameter information and a new iteration ending condition. Meanwhile, to overcome the negative effects of the voltage estimation errors on the identification accuracy, in addition to the nonlinear compensation, a preprocessing scheme of sampled data was proposed, where the data in the certain range of current zero-crossing were removed. The experimental results show that the scheme can identify the direct axis and quadrature axis inductances and the permanent magnet flux quickly and accurately without affecting the normal operation of the system.

Permanent magnet synchronous motor, parameter identification, particle swarm optimization algorithm, data preprocessing

10.19595/j.cnki.1000-6753.tces.211470

TM351

安徽省科技重大专项（202003a05020029）和台达电力电子科教发展计划项目（DREK2020004）资助。

2021-09-15

2021-12-17

李 婕 女，1996年生，硕士，研究方向为永磁同步电机驱动控制。E-mail: lj64_youxiang@163.com

杨淑英 男，1980年生，教授，博士生导师，研究方向为风力发电系统、电驱动系统。E-mail: yangsyhfah@163.com（通信作者）

（编辑 陈 诚）