一种新型多电平逆变器及其模块化分析

王要强 李 娜 赵朝阳 陈天锦 梁 军

一种新型多电平逆变器及其模块化分析

王要强1,2李 娜1,2赵朝阳1,2陈天锦3梁 军1,4

（1. 郑州大学电气工程学院 郑州 450001 2. 河南省电力电子与电能系统工程技术研究中心 郑州 450001 3. 河南省智能充电技术重点实验室 许昌 461000 4. 卡迪夫大学工程学院 卡迪夫 CF243AA）

为改善传统多电平逆变器有源器件数量较多以及扩展结构复杂的问题，该文提出一种降低器件数量且可模块化扩展的多电平逆变器。该逆变器由分压电容单元、开关电容单元和两个半桥组成，使用1个直流电源、4个电容、8个开关管和2个二极管实现2倍电压增益和九电平交流输出电压。该逆变器通过2个半桥代替后端H桥转换输出电压极性，可以有效降低开关管总电压应力；在所提逆变器的模块化扩展结构中，电容逐级充电的工作方式进一步提高了电压增益和输出电平数。该文研究逆变器的工作状态、调制策略、电容分析、参数计算并进行拓扑对比。最后，通过仿真与实验验证了所提逆变器的可行性和理论分析的正确性。

逆变器 多电平 开关电容 电压自平衡 模块化

0 引言

近年来，能源紧张与环境恶化问题愈发严峻，清洁可再生能源的研发迫在眉睫[1]。为了将新能源所发电能传输到电网或本地负载，而使功率变换器得到广泛研究[2-3]。其中，多电平逆变器由于能够提供可靠高质量的输出电压，在直流电转化为交流电方面有其独特优势[4-6]。

传统多电平逆变器主要分为二极管钳位型[7-8]、飞跨电容型[9-10]及级联H桥型[11-12]。随着输出电平数的升高，二极管钳位型和飞跨电容型拓扑结构中器件数量显著增加，且二者均存在电容电压不平衡的问题，需要辅助电路和复杂的控制算法来维持电容电压平衡。级联H桥型拓扑通过级联H桥模块提高其输出电平，使用非对称独立直流电源可合成最佳输出电平。但是，多个独立直流电源的需求为逆变器设计带来困难。

开关电容多电平逆变器利用电容与电源“串联充电、并联放电”的工作方式将电容作为储能元件参与放电，可有效提高输出电压增益和输出电平数量，且具有电容电压自平衡、升压能力强、功率密度大等优点，在近些年被广泛研究。文献[13-16]所提逆变器拓扑由开关电容升压单元和后端H桥构成，可大幅提高输出电压幅值。该类拓扑仅需单个直流电源，且开关电容升压单元的结构易于扩展，输出水平随其扩展而升高。其中，文献[13]所提拓扑的开关电容单元由三个开关管和一个电容构成，每个电容的额定电压相等；文献[14]所提拓扑在文献[13]的基础上用二极管替换部分开关管，大幅降低开关管数量，然而过分追求开关管数量的降低使得该拓扑不具备独立带感性负载的能力；文献[15]改进了拓扑结构中电容的充放电模式，利用电容逐级充电的工作方式提高电容电压幅值，从而提高输出电压增益；文献[16]所提拓扑利用钳位电容将直流电压均分，分压后的钳位电容与开关电容串联可实现更高的输出电平数，从而降低了输出电压总谐波畸变率（Total Harmonic Distortion, THD）。然而上述拓扑结构均需使用H桥实现逆变，H桥开关管的电压应力为峰值输出电压，使得开关器件承受的总电压应力（Total Standing Voltage, TSV）较高。文献[17-19]取消了后端H桥，有效降低了TSV。其中，文献[17]所提拓扑结构中开关管的电压应力均为输入电压；文献[18]所提拓扑结构利用开关管与电容的交叉连接，使得开关管的电压应力均被限制

在输入电压的2倍以内，且不随输出水平的升高而升高；文献[19]所提拓扑中电压应力为输出电压峰值的开关管数量减半。然而，上述拓扑的开关管数量较高，不仅增大了控制难度，也增加了变换器的体积和成本。

在上述研究的基础上，为进一步降低有源器件数量、简化逆变器扩展结构，本文提出一种新型开关电容多电平逆变器。开关电容单元仅包含2个电容、2个开关管和2个二极管，不仅结构简单对称且开关管互补的工作状态有利于简化逆变器的控制；分压电容和开关电容的逻辑组合使得逆变器以较少数量的器件实现2倍电压增益和九电平交流电压输出；所提逆变器的模块化扩展结构中，后级电容由前级电容串联充电的工作方式可进一步提高输出电压增益和输出电平数。此外，所提逆变器无需后端H桥即可生成双极性输出电压，有利于降低TSV。

1 逆变器拓扑结构及工作原理

1.1 拓扑结构

图1为本文所提多电平逆变器拓扑结构，该拓扑由分压电容单元、开关电容单元以及两端半桥构成。分压电容单元包含串联的分压电容a、b与双向开关管VT（由两个反向串联的开关管构成）；分压电容与直流电源dc并联充电且两电容的额定电压均为0.5dc；通过控制双向开关管VT的闭合与关断，控制分压电容或直流电源向输出端提供±0.5dc、±dc的电平。开关电容单元包含开关管S1、S2，电容1、2以及二极管VD1、VD2，通过控制S1、S2的闭合与关断实现电容1、2与直流电源的串并联。开关管S3、S4和S5、S6组成的两端半桥实现分压电容单元和开关电容单元输出电平的选择和逻辑组合，以及输出电压正负极性的转换。基于以上分压电容单元、开关电容单元和半桥结构，所提拓扑可以输出0、±0.5dc、±dc、±1.5dc和±2dc共九个电平。

图1 多电平逆变器拓扑结构

1.2 工作原理

图2为所提逆变器的九种工作模态，图中，虚线为阻性负载的电流路径，点画线为电容的充电电流路径，点线为感性负载的反向电流路径。表1为各个输出状态下功率器件的工作情况，0和1分别表示开关管的导通和关断状态；“C”、“D”和“-”分别表示电容的充电、放电和保持状态。为简化分析，假设拓扑中的电容值足够大，电容的电压纹波可以忽略；所有开关器件均无导通压降和导通电阻；输入电源为理想直流电源，即电压值恒定且没有串联阻抗。

表1 逆变器各输出状态下器件的工作状态

Tab.1 Working states of devices in each output state of the inverter

模态1：所提逆变器输出电压为+2dc。在此模态中开关管S1、S4、S5闭合，电容2被充电至dc，电容1与直流电源串联为负载供电。

模态2：所提逆变器输出电压为+1.5dc。在此模态中开关管S1、VT、S5闭合，电容2被充电至dc，电容1与分压电容a串联为负载供电。

模态3：所提逆变器输出电压为+dc。在此模态中开关管S2S4、S5闭合，电容1被充电至dc，直流电源和分压电容a、b并联为负载供电。

模态4：所提逆变器输出电压为+0.5dc。在此模态中开关管S2VT、S5闭合，电容1被充电至dc，分压电容a单独为负载供电。

模态5：所提逆变器输出电压为0。在此模态中开关管S2闭合，电容1被充电至dc，半桥的开关管S3、S5连接到输出端，输出为0。

模态6：所提逆变器输出电压为–0.5dc。在此模态中开关管S1、VT、S6闭合，电容2被充电至dc，分压电容b单独为负载供电。

模态7：所提逆变器输出电压为–dc。在此模态中开关管S1、S3、S6闭合，电容2被充电至dc，直流电源和分压电容a、b并联为负载供电。

模态8：所提逆变器输出电压为–1.5dc。在此模态中开关管S2、VT、S6闭合，电容1被充电至dc，分压电容b与直流电源串联为负载供电。

模态9：所提逆变器输出电压为–2dc。在此模态中开关管S2、S3、S6闭合，电容1被充电至dc，电容2与直流电源串联为负载供电。

从逆变器输出状态的电流回路可以看出，各个状态均具有与输出电平相对应的反向续流回路。当输出电压为0、±0.5dc、±dc时，反向电流路径由点线标注，其余输出状态的反向电流路径均与正向流通路径相同，即电路具有带感性负载的能力。此外，如图2和表1所示，在模态1、2、8、9中，开关管S1和S2可以同时参与电容的充电和放电过程，从而有利于减少拓扑结构中开关管数量。

本文所提逆变器可根据实际需求作为并网逆变器用于光伏发电等新能源领域。光伏阵列产生的电能经过逆变器的电能变换，除供给负载外，多余电能可经过滤波器输入电网[20]。完整的电路及控制框图如图3所示，在该电路中，控制并网电流g的幅值与给定值m相同，而相位通过锁相环（Phase Locked Loop, PLL）与电网电压g的相位保持一致，并网电流与指令值*相比后，经准比例谐振控制器i()得到的参考值r经电网电压前馈后可得控制策略的调制电压M。光伏电池可直接通过所提逆变器进行逆变升压，无须使用传统系统中的变压器[21]。

图3 单相并网逆变器及其控制结构

2 调制策略分析

多电平逆变器常见调制策略有空间矢量调制[22]、载波层叠脉宽调制[23]、混合调制[24]和消除特定谐波调制[25]等。本文采用同相载波层叠PWM方法对所提逆变器进行调制，该方法具有实现简单、THD小等优点。所提逆变器的PWM如图4所示，用8个幅值和频率相同的三角载波（t1～t8）与正弦调制波（ref）进行比较，产生的脉冲根据开关状态进行逻辑组合来控制开关管的开通和关断。调制比和电压增益分别定义为

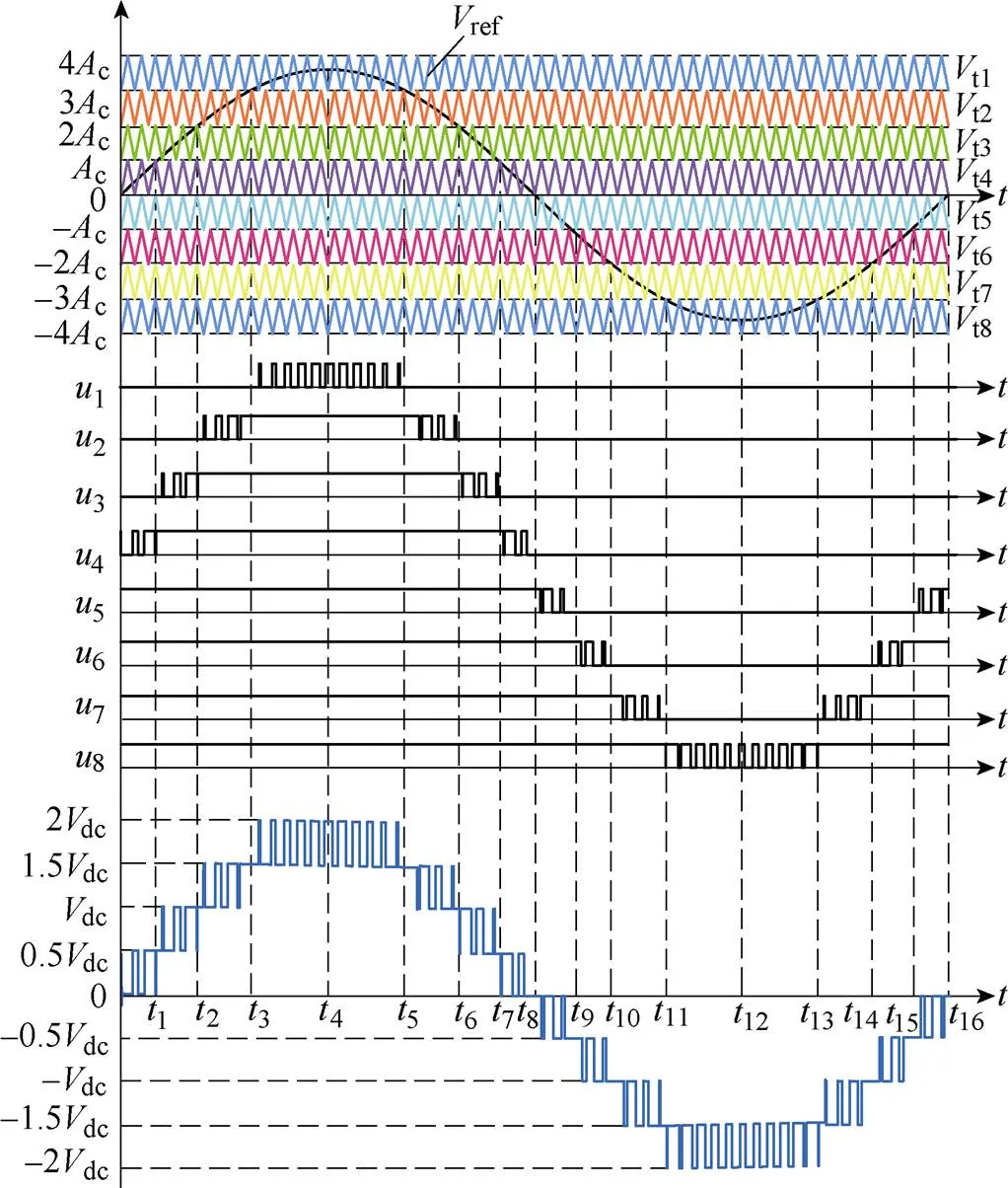
图4 所提逆变器的PWM

式中，c和ref分别为三角载波和正弦调制波幅值；out和dc分别为输出电压和直流输入电压。

通过调整调制比可以实现对输出电平数和电压增益的控制。在该调制方法中，调制比与输出电平数和电压增益的关系见表2。

表2 不同调制比下的输出电平数、电压增益

Tab.2 Output levels and voltage gain under different modulation ratio

t1～t8与ref比较形成控制开关管通断所需的基本脉冲1～8。将这些脉冲进行相应的逻辑组合，进而控制各开关管的工作状态，各开关管控制信号的逻辑关系分别为

开关管在一个完整周期内的工作状态如图5所示。通过控制开关管S1、S2和S5、S6的导通关断，控制电容C1和C2的充放电。由图5可以看出，开关管S1与S2工作状态互补；开关管S5与S6工作状态互补。由驱动波形的交替变化可以看出，电容C1和C2等量充放电。

3 电容分析及其容值计算

在开关电容多电平逆变器中，电容放电过程中会产生电压纹波，电容电压纹波过大会导致电源转换效率下降和输出波形THD上升。因此，应在满足电压纹波要求的条件下选择合适的电容值。

电容的电压纹波出现在其最大放电时间，确定电容的最大放电时间即可计算电容值。对图2和表1分析可得，电容1、a的最大放电时间出现在正半周期，电容2b的最大放电时间出现在负半周期，在一个完整的工作周期内二者最大放电时间相同，因此在本节中只对电容1和a分析计算。对逆变器工作模态分析可得，电容1的最大放电时段为2～6，电容a的最大放电时段为2～3。在载波层叠调制方式下，2～6可以表示为

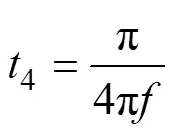
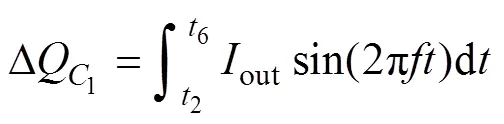
式中，out为逆变器输出电流。假定电容电压纹波小于额定电压C的10%，则电容12和a、b必须满足

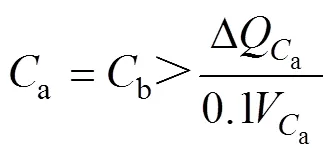
4 拓扑扩展及对比分析

4.1 拓扑扩展结构

本文所提拓扑具备模块化扩展能力，将开关电容单元向右扩展，得到如图6所示扩展拓扑结构。扩展拓扑的工作方式与图2拓扑的工作模态分析相似，通过控制直流电源与各开关电容单元的串并联转换实现电容在逆变器工作周期内的充放电以及逆变器多电平交流电压输出。

图6 模块化扩展拓扑结构

由图6可知，通过闭合开关管S11（S12），直流电源给电容12（11）充电至dc。应用逐级充电的方法，第一个模块中的电容11和12的串联组合经过S22和VD21（S21和VD22）在不同的时段为21（22）充电至2dc。对于第个开关电容单元，(i1)1和(i1)2的串联组合通过S2和VD1（S1和VD2）对C1（C2）充电至2-1dc。后级开关电容单元中电容的充电方法以此类推。此种充电方式下，电容电压可以维持在较高水平，进一步提高了输出电压增益和输出电平数。

当逆变器包含个开关电容单元时，直流电源和分压电容可以向输出端提供的电平为±0.5dc和±dc；每级开关电容电路可提供的电平为±2-1dc（=1, 2,…,）；通过分压电容单元与开关电容单元的逻辑组合，在负载侧可以获得0，±0.5dc,…, 2Vdc共2+2+1个输出电平，输出电压峰值为2Vdc。

4.2 拓扑对比分析

为了比较拓扑性能，在此将具有扩展能力的单电源多电平逆变器与本文所提逆变器在输出电平数同为2+1（≥4）的条件下进行对比分析。比较的主要指标包括功率器件数量、逆变器增益以及TSV，考虑到文献[14-17]与本文所提拓扑升压增益不完全相同，通过所有开关器件上的总电压应力与拓扑的输出峰值电压之比来计算TSV。不同拓扑的比较结果见表3，不同拓扑器件数量比较如图7所示。

表3 不同拓扑的比较结果

Tab.3 Comparative results among different topologies

图7 不同拓扑器件数量比较

分析可得，在本文所提拓扑的扩展结构中，每增加一个开关电容单元，仅增加两个开关和两个电容，然而输出电平数量几乎增加了一倍，电压增益变为原来的2倍。由表3和图7可知，与文献[14-17]相比，本文所提拓扑开关管数量最少；输出电平数较低时，本文所提拓扑由于前端分压电容和开关电容单元的串联导致电容数目过高，但随着的增长，本文所提拓扑的电容数量呈对数增长，电容数量逐渐成为最优；对比结果表明，本文所提拓扑模块化扩展后，有源器件总数随输出级数呈对数曲线增加，低于其他线性增加的拓扑，这有利于降低变换器成本、提高变换器功率密度。

本文所提逆变器升压能力较弱，这是由于前级分压电容提供了±0.5dc的输出电平，同时这将使得逆变器扩展之后输出电平数显著提升。相较于文献[14-16]，本文所提拓扑未应用末端H桥而具有较低的TSV。过高的电压应力不仅会限制这些逆变器的中/高压应用，还会使逆变器成本上升。在文献[17]中，所有开关管的电压应力都在直流电源dc以内，从而降低了TSV。然而，该拓扑使用了较多数量的开关管，大量的开关管不仅提高了控制的复杂度，也会使变换器成本上升。

5 仿真与实验分析

5.1 仿真及结果分析

为验证所提多电平逆变器理论分析的正确性，在Matlab/Simulink仿真平台对其进行仿真证明，具体电路元件及其参数见表4。

表4 电路元件及其参数

Tab.4 Parameters of circuit components

图8为所提逆变器在表4参数下的仿真结果。图8a、图8b分别为所提逆变器在阻性负载和阻感性负载下的输出电压、输出电流波形。由仿真结果可知，逆变器以九电平的形式输出电压，当输入电压为30V时，输出电压峰值约为60V；在阻性负载下，逆变器以九电平的形式输出电流，输出电流峰值约为1.96A；在阻感性负载下，输出电流更接近正弦波，输出电流峰值约为1.72A。图8c为阻感性负载下分压电容和开关电容的电压波形，开关电容1、2的电压在28.4～29.3V之间波动，最大电压纹波为1.6V（5.3%）；分压电容a、b的电压在14.6～15.4V之间波动，最大电压纹波为0.4V（4%）。结果表明，电容电压在逆变器工作周期内波动范围小，工作状态稳定，符合第3节中电压纹波系数小于10%的设定原则。对电容电压的进一步研究表明，电容1在输出电压为60V和45V时放电；电容2在输出电压为–60V和–45V时放电；其余输出电平下两电容均处于充电或保持状态，这与图2和表1中对逆变器各个工作模态的分析一致。

图8 所提逆变器仿真波形

为验证所提逆变器的动态调节能力，根据图3所示的控制框图，搭建仿真模型，具体仿真参数为：直流输入电压200V，电网电压220V/50Hz，滤波电感5mH，电容2 200mF。当逆变器的输出功率在500～1 000W之间跳变时，仿真波形如图9所示。可以看出，并网电流迅速变化到目标值，具有良好的动态响应。

图9 输出功率在500W至1kW跳变时的仿真波形

5.2 实验及结果分析

为进一步验证所提逆变器的可行性，搭建一台小型实验样机验证其稳态和动态性能，实验参数与仿真参数相同，实验平台如图10所示。

图10 实验平台

5.2.1 稳态实验及结果分析

图11为所提逆变器在50Hz基波频率、阻感性负载条件下的实验波形，输出电压为九电平阶梯波，电压峰值接近60V，约为输入电压的2倍，阻感性负载使输出电流更接近正弦波。图12、图13分别为稳态下电容1、2和a、b的电压波形。由实验结果可知，逆变器稳态实验结果与仿真结果基本一致，验证了所提拓扑理论分析的正确性。

图11 稳态下输出电压、电流的实验波形

图12 稳态下C1、C2电压波形

图13 稳态下Ca、Cb电压波形

5.2.2 动态实验及结果分析

逆变器运行过程中可能发生工作条件的变化，本节模拟输入电压突变、调制比突变、负载突变和调制波频率突变四种情况在电路元件及参数不变的条件下进行实验，验证所提逆变器的动态响应能力。

图14为所提逆变器在输入电压突变时的实验结果。由图可见，当输入电压变化时，逆变器的输出电压、电流随之变化后迅速进入新的稳态。当输入电压从30V变化至20V时，输出电压、电流在短时间内下降至期望值并稳定在该状态；输入电压从20V变化至30V时，输出状态也能迅速回到预期状态。

图15为所提逆变器在调制比突变时的实验结果。由图可知，当从0.9变化至0.5时，输出电平数从九减小至五，电压增益从2减小至1。当从0.5变化至0.9时，逆变器迅速恢复九电平电压输出和2倍增益的输出状态，与表2中的分析一致。

图15 调制比突变的输出波形

图16为所提逆变器在负载突变时的输出结果。由实验结果分析可得，输出电压状态不受负载变化影响，输出电流随负载变化并迅速稳定在期望值。上述结果验证了逆变器具有适应负载大范围变化的工作能力。

图16 负载突变的输出波形

图17为调制波频率由50Hz突变至25Hz和100Hz的实验结果。由图可知，逆变器输出频率跟随调制波频率的变化而变化，并迅速进入新的稳态。

6 结论

1）本文提出了一种新型多电平逆变器。所提拓扑的开关电容单元结构简单，有利于简化逆变器的控制。通过分压电容和开关电容的逻辑组合，以单电源输入和较少数量的器件即可实现九电平输出和2倍的电压增益。

2）在所提逆变器的模块化扩展结构中，后级电容由前级电容串联充电，此种充电方式进一步提高了输出电压增益和输出电平数。当逆变器结构中具备个开关电容单元时，输出电压峰值达到2Vdc，输出电平数达到2+2+1。

3）在拓扑的扩展结构中，本文所提拓扑结构的有源器件数量增长趋势缓慢。与近年来提出的开关电容多电平逆变器的比较结果表明，本文所提拓扑结构在输出电平数升高之后，在功率器件数量方面有明显优势，这有利于降低变换器成本、提高变换器功率密度。

4）最后，搭建的实验模型验证了所提拓扑理论分析的正确性及其可行性，结果表明，逆变器在稳态和动态条件下都具有良好的工作性能。

[1] 朱泽安, 周修宁, 王旭, 等. 基于稳暂态联合仿真模拟的区域多可再生能源系统评估决策[J]. 电工技术学报, 2020, 35(13): 2780-2791.

Zhu Zean, Zhou Xiuning, Wang Xu, et al. Evaluation and decision-making of regional multi-renewable energy system based on steady-transient integrated simulation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2780-2791.

[2] 张峰, 谢运祥, 胡炎申, 等. 临界模式混合光伏微型逆变器的特性分析[J]. 电工技术学报, 2020, 35(6): 1290-1302.

Zhang Feng, Xie Yunxiang, Hu Yanshen, et al. Characteristics analysis for a boundary conduction mode hybrid-type photovoltaic micro-inverter[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(6): 1290-1302.

[3] 李伟, 王辉, 黄守道, 等. 全桥三电平DC-DC变换器优化控制策略[J]. 电工技术学报, 2021, 36(16): 3342-3353.

Li Wei, Wang Hui, Huang Shoudao, et al. Optimal control for the full-bridge three-level DC-DC con- verter[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3342-3353.

[4] 丁凯, 邹云屏, 蔡政英, 等. 一种新型单相不对称五电平逆变器[J]. 中国电机工程学报, 2004, 24(11): 116-120.

Ding Kai, Zou Yunping, Cai Zhengying, et al. A novel single-phase asymmetric 5-level inverter[J]. Proceedings of The CSEE, 2004, 24(11): 116-120.

[5] 邱继浪, 何英杰, 焦乾明, 等. 非隔离型三电平逆变器漏电流抑制与中点电位平衡控制[J]. 电力系统自动化, 2021, 45(17): 161-170.

Qiu Jilang, He Yingjie, Jiao Qianming, et al. Leakage current suppression and balance control of neutral point potential for three-level transformerless inver- ter[J]. Automation of Electric Power Systems, 2021, 45(17): 161-170.

[6] 叶满园, 任威, 李宋, 等. 基于控制载波自由度的级联H桥逆变器改进型PWM技术[J]. 电工技术学报, 2021, 36(14): 3010-3021.

Ye Manyuan, Ren Wei, Li Song, et al. Improved PWM technology of cascaded H-bridge inverter based on control of carrier degree of freedom[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(14): 3010-3021.

[7] 刘庆丰, 冷朝霞. 二极管钳位型逆变器双频感应加热电源的解耦控制[J]. 中国电机工程学报, 2019, 39(6): 1783-1791, 1874.

Liu Qingfeng, Leng Zhaoxia. The decoupling control of double-frequency induction heating power supply based on diode clamped inverter[J]. Proceedings of the CSEE, 2019, 39(6): 1783-1791,1874.

[8] Abdullah R, Rahim N A, Raihan S R S, et al. Five-level diode-clamped inverter with three-level boost converter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5155-5163.

[9] 庄桂元, 张兴, 刘威, 等. 带飞跨电容的三电平拓扑中SiC MOSFET过电压与过电流保护[J]. 电工技术学报, 2021, 36(2): 341-351.

Zhuang Guiyuan, Zhang Xing, Liu Wei, et al. Over- voltage and overcurrent protection of SiC MOSFET in three-level topology with flying capacitor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(2): 341-351.

[10] He Liangzong, Cheng Chen. A flying-capacitor- clamped five-level inverter based on bridge modular switched-capacitor topology[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7814-7822.

[11] 林先辉, 郭谋发, 张伟骏, 等. 用于配电网故障消弧的级联H桥多电平变换器设计及仿真[J]. 电气技术, 2015, 16(12):10-14, 21.

Lin Xianhui, Guo Moufa, Zhang Weijun, et al. Design and simulation of cascaded H-bridge multilevel converters used for faults arc extinguishing of distribution networks[J]. Electrical Engineering, 2015, 16(12): 10-14, 21.

[12] 叶满园, 康力璇, 陈乐, 等. 级联多电平逆变器优化调制策略[J]. 高电压技术, 2019, 45(11): 3612- 3619.

Ye Manyuan, Kang Lixuan, Chen Le, et al. Opti- mization of modulation strategy for cascaded multi- level inverter[J]. High Voltage Engineering, 2019, 45(11): 3612-3619.

[13] Hinago Y, Koizumi H. A switched-capacitor inverter using series/parallel conversion with inductive load[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 878-887.

[14] Ye Yuanmao, Cheng K W E, Liu Junfeng, et al. A step-up switched-capacitor multilevel inverter with self-voltage balancing[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6672-6680.

[15] Barzegarkhoo R, Kojabadi H M, Zamiry E, et al. Generalized structure for a single phase switched- capacitor multilevel inverter using a new multiple DC link producer with reduced number of switches[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5604-5617.

[16] 王要强, 王凯歌, 周成龙, 等. 单相中点箝位开关电容多电平逆变器及其控制[J]. 电力自动化设备, 2020, 40(7): 89-95.

Wang Yaoqiang, Wang Kaige, Zhou Chenglong, et al. Single phase neutral-point-clamped switched-capacitor multilevel inverter and its control[J]. Electric Power Automation Equipment, 2020, 40(7): 89-95.

[17] Taghvaie A, Adabi J, Rezanejad M. A self-balanced step-up multilevel inverter based on switched-capacitor structure[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 199-209.

[18] Samizadeh M, Yang Xu, Karami B, et al. A new topology of switched-capacitor multilevel inverter with eliminating leakage current[J]. IEEE Access, 2020, 8: 76951-76965.

[19] Siddique M D, Mekhilef S, Mohamed Shah N, et al. A new switched-capacitor based Boost multilevel inverter topology with higher voltage gain[J]. IET Power Electronics, 2020, 13(14): 3209-3212.

[20] Zhu Xiaonan, Wang Hongliang, Zhang Wenyuan, et al. A novel single-phase five-level transformer-less photovoltaic (PV) inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 329- 338.

[21] 管月, 李磊, 张晋川. 适合高输入电压的高频隔离逆变器[J]. 电力系统自动化, 2020, 44(11): 163-170.

Guan Yue, Li Lei, Zhang Jinchuan. High-frequency isolated inverter for high input voltage[J]. Auto- mation of Electric Power Systems, 2020, 44(11): 163-170.

[22] 吴学智, 刘亚东, 黄立培. 三电平电压型逆变器空间矢量调制算法的研究[J]. 电工电能新技术, 2002, 21(4): 16-19.

Wu Xuezhi, Liu Yadong, Huang Lipei. Research on space vector modulation algorithm for three-level PWM voltage source inverter[J]. Advanced Techno- logy of Electrical Engineering and Energy, 2002, 21(4): 16-19.

[23] McGrath B P, Holmes D G. Multicarrier PWM strategies for multilevel inverters[J]. IEEE Transa- ctions on Industrial Electronics, 2002, 49(4): 858- 867.

[24] 叶满园, 吴韩. 混合CHB逆变器优化调制策略的研究[J]. 电力电子技术, 2019, 53(9): 95-98.

Ye Manyuan, Wu Han. Research on hybrid CHB inverter optimization modulation method[J]. Power Electronics, 2019, 53(9): 95-98.

[25] 杨克虎, 唐欣, 张奇, 等. 阶梯波多电平变换器特定谐波消除的完全解[J]. 电机与控制学报, 2017, 21(2): 27-34.

Yang Kehu, Tang Xin, Zhang Qi, et al. Complete solutions for selective harmonic elimination problem of multilevel staircase converter[J]. Electric Machines and Control, 2017, 21(2): 27-34.

A New Type of Multilevel Inverter and Its Modular Analysis

1,21,21,231,4

（1. School of Electrical Engineering Zhengzhou University Zhengzhou 450001 China 2. Henan Engineering Research Center of Power Electronics and Energy Systems Zhengzhou 450001 China 3. Henan Key Laboratory of Intelligent Charging Technology Xuchang 461000 China 4. School of Engineering Cardiff University Cardiff CF243AA UK）

In order to improve the problems of the large number of active components and the complex expansion structure of the traditional multilevel inverter, this paper proposes a multilevel inverter that reduces the number of components and can be modularly expanded. The inverter is composed of a voltage divider capacitor unit, a switched capacitor unit and two half bridges. It uses 1 DC power supply, 4 capacitors, 8 switches and 2 diodes to achieve double voltage gain and a nine-level AC output voltage. Two half-bridges are used in the proposed inverter instead of the back-end H-bridge to convert the output voltage polarity, which can effectively reduce the total voltage stress of the switches. In the modular expansion structure of the proposed inverter, the step-by-step charging method of the capacitors further improves the voltage gain and the output level number. This paper includes the working states, modulation strategy, capacitance analysis, parameter calculation, and topology comparison of the proposed inverter. Finally, the feasibility of the proposed inverter and the correctness of the theoretical analysis are verified through simulation and experiment.

Inverter, multilevel, switched capacitor, voltage self-balancing, modular

10.19595/j.cnki.1000-6753.tces.211002

TM464

国家自然科学基金项目（51507155）、河南省高等学校青年骨干教师项目（2019GGJS011）和河南省重点研发与推广专项项目（222102520001）资助。

2021-07-07

2021-11-08

王要强 男，1982年生，博士，副教授，主要研究方向为电力电子变换、可再生能源发电、电机驱动控制等。E-mail: WangyqEE@163.com

赵朝阳 男，1992年生，博士，讲师，主要研究方向为电力电子功率变换理论及其应用。E-mail: zhaoyangzhao@zzu.edu.cn（通信作者）

（编辑 陈 诚）