基于PSO-Gabor特征增强的钢板表面缺陷识别研究

姜乐兵，宋飞虎，裴永胜，吴 鑫，李臻峰

(1.江南大学机械工程学院，江苏省食品先进制造装备技术重点实验室，江苏无锡 214122；2.江苏科贸新材料科技有限公司，江苏江阴 214000)

0 引言

钢板作为钢材加工的主要材料，在生产制造、交通运输等领域得到广泛应用[1]。在钢板制造过程中，设备和工艺会造成热轧带钢表面出现裂纹和麻点等不同缺陷，这不仅影响产品美观，还对产品的耐磨性、抗疲劳强度等性能有较大影响，严重降低产品的使用寿命[2]。因此，为保证产品质量，对钢板表面的缺陷进行检测与识别研究具有重要意义。

为克服人工检测方法效率低、主观性强等缺点，徐科等[3]结合Tetrolet变换和核保局投影算法对热轧钢板表面缺陷图像实现低维特征的提取，利用支持向量机实现热轧钢板表面缺陷的识别，该方法对热轧钢板表面8类常见缺陷具有较高的识别率，但Tetrolet变换耗时较长，难以实现缺陷的在线检测。李爱莲等[4]结合LBP和LBQ进行特征提取，利用蚁群与粒子群优化支持向量机的惩罚参数和核函数参数实现缺陷分类。随着数据集的扩充及网络结构逐渐优化，卷积神经网络(CNN)用于缺陷分类成为研究热点[5-7]。汤勃等[8]选用特征灰度值一阶概率分布和x方向投影分布对钢板表面缺陷图像进行标记，将标记图像输入到卷积神经网络中实现钢板表面缺陷识别，但该算法需要先对缺陷图像进行预处理，检测步骤较复杂。

因此，为提高钢板表面缺陷的识别准确率，同时避免繁琐的人为特征提取过程，本文提出了一种基于PSO-Gabor特征增强的钢板表面缺陷识别方法，能够有效增强缺陷特征，准确快速地识别钢板表面6类缺陷，极大地提升检测速度与识别准确率。

1 钢板表面缺陷识别算法

基于PSO-Gabor特征增强的钢板表面缺陷识别主要包括3个阶段：

(1)利用PSO算法对Gabor滤波器进行参数寻优；

(2)基于最优参数构造Gabor滤波器对缺陷图像进行滤波，并计算滤波后图像的能量响应值以获得能量图；

(3)构建CNN，将能量图作为模型输入，实现缺陷图像的识别。

算法流程如图1所示。

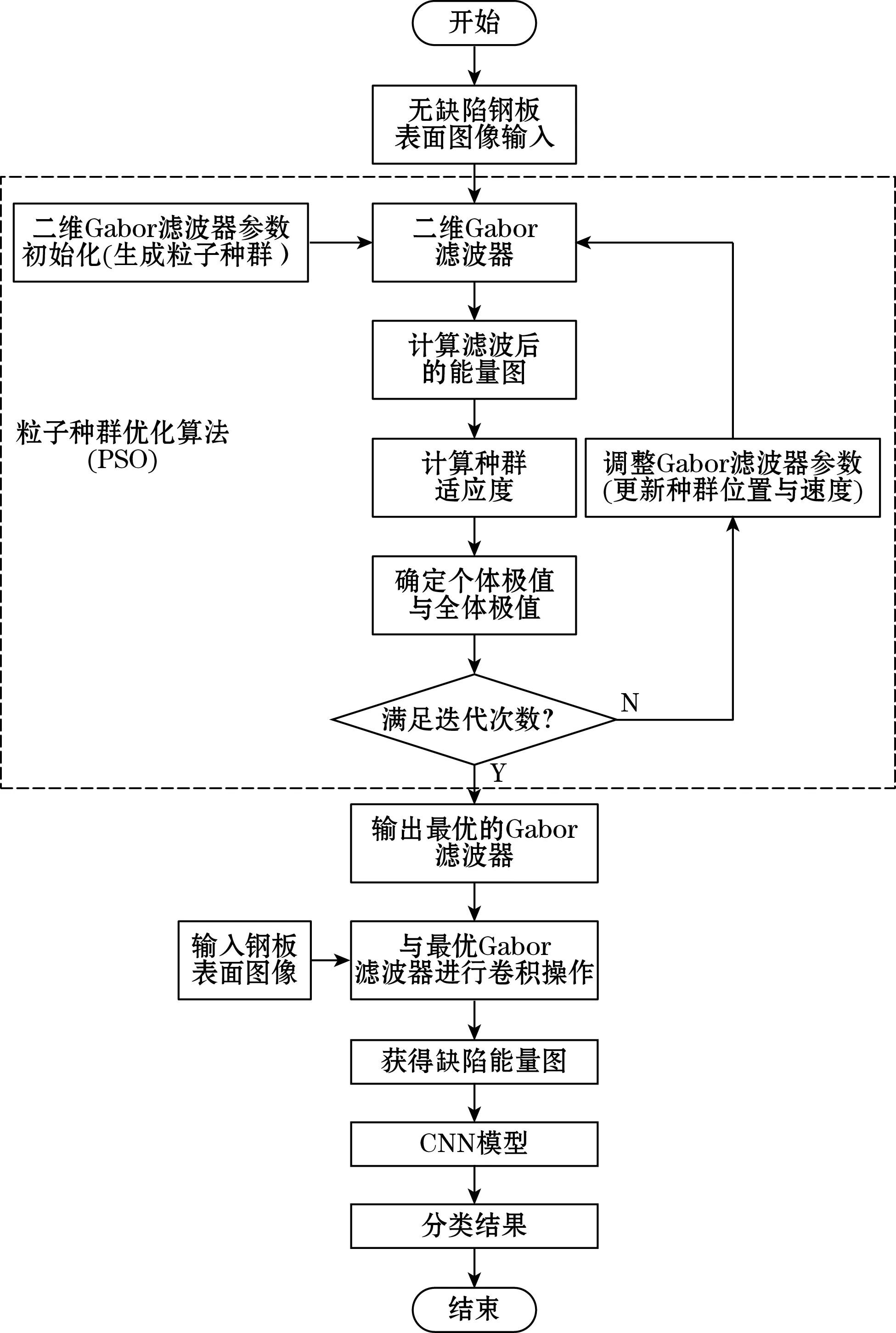
图1 缺陷识别流程图

1.1 二维Gabor滤波器

1985年，Daugman提出了二维Gabor函数[9]。二维Gabor滤波器的滤波原理为：图像在不同的频率和带宽上进行滤波，符合滤波器频率范围的信号进行提取，其他超过频率范围的信号被抑制[10]。时域中二维Gabor滤波器如式(1)所示：

(1)

式中：x和y分别表示Gabor滤波器的横纵坐标；φ为频率；θ为方向；σ为尺度；x′=xcosθ+ysinθ,y′=-xsinθ+

ycosθ。

输入图像f(x,y)与二维Gabor滤波器进行卷积可得到输出图像g(x,y|σ,φ,θ)，如式(2)所示：

(2)

式中：k取决于二维Gabor滤波器滤波窗口尺寸W；

W=2k+1。

输出图像g(x,y|σ，φ，θ)的能量响应表达式如式(3)所示：

(3)

式中：gRe(x,y|σ,φ,θ)和gIm(x,y|σ,φ,θ)分别为输出图像g(x,y|σ，φ，θ)的实部与虚部。

从式(1)可得，Gabor滤波器由频率φ、方向θ及尺度σ决定，Gabor滤波器选取不同参数获得不同的滤波效果，在时域和频域中产生不同的能量响应。研究表明，低频率、小尺度Gabor滤波器提取图像全局特征，高频率、大尺度Gabor滤波器获得图像细节特征[11-13]；同时滤波窗口尺寸W也影响Gabor滤波器对图像的滤波效果，Gabor滤波器小窗口提取图像整体特征，大窗口获得图像局部特征[11]。此外，滤波窗口尺寸还影响滤波速度，窗口尺寸越小，滤波速度越快。随着Gabor滤波器的3个参数和滤波窗口尺寸的改变，滤波后图像的能量响应也会有所不同。缺陷图像经过不同参数的Gabor滤波器滤波后的能量响应见图2。

图2中，每行代表其他3个参数保持相同，另一个参数逐渐增大的能量图对比结果。由图2可知，频率φ、方向θ、尺度σ以及滤波窗口尺寸W越小，缺陷图像的整体特征更明显，随着参数值增大，缺陷的细节特征逐渐被提取，当继续增大时，缺陷细节会逐渐消失。综上所述，φ、θ、σ以及W对Gabor滤波器的滤波性能有较大影响，因此，Gabor滤波器的参数寻优对提升滤波性能有重要意义。

(a)W=27，θ=5π/6,σ=1

1.2 PSO算法求解Gabor滤波器最优参数

PSO算法是一种全局搜索算法，通过群体中个体间的协作与信息共享来寻求最优解，其收敛速度快、无繁杂的参数设置，目前广泛用于函数求解与模式识别等领域。本文采用PSO算法对Gabor滤波器的频率φ、方向θ、尺度σ以及滤波窗口尺寸W进行寻优。PSO算法中每个粒子都代表问题的一个潜在解，每个粒子对应着一个适应度函数决定的适应度值[14-15]。粒子的速度及位置更新公式为：

(4)

(5)

搜索前期较大的w值有利于全局搜索，在搜索后期适当减小则可以加强局部搜索能力[16]，因此，对w的值线性递减可以提高粒子群寻优性能，其计算公式[17]如式(6)所示：

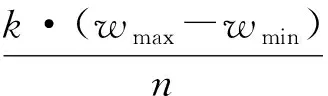
(6)

式中：k为当前迭代次数；n为迭代次数；wmax=0.9；

wmin=0.4。

根据Fisher准则构造目标函数作为PSO算法对Gabor滤波器参数进行迭代寻优的适应度函数，适应度函数如式(7)所示：

(7)

式中：μE和σE分别为无缺陷图像经过Gabor滤波器滤波后图像的能量响应均值与能量响应标准差。

在特定的搜索空间中，要找到与无缺陷图像特征相匹配的Gabor滤波器参数，则需要使图像能量响应均值μE达到最大，并使能量响应标准差σE达到最小，也就需要使适应度函数Z的值达到最大，即可获得Gabor滤波器的最优参数。

本文设定PSO算法的初始种群数为50，迭代次数为50。粒子群经过50次迭代寻优获得Gabor滤波器的4个最优参数值，如表1所示。

表1 Gabor滤波器最优参数值

根据表1的最优参数构造最优二维Gabor滤波器，与缺陷图像进行卷积操作，并根据式(3)对滤波后的图像求解能量响应值从而获得能量图，部分能量图如图3所示，其中左图为缺陷原图，右图为对应的能量图。从图3可以直观地看出，能量图中无缺陷区域与缺陷区域能量响应值差别明显，缺陷区域更加突出。

(a)裂纹

(f)划痕

为了进一步体现所构造的最优Gabor滤波器的滤波效果，图4列出了3种增强方法对划痕图像的处理结果，从图4可以看出，直方图均衡化处理后的划痕图像出现较多伪缺陷区域，进一步增大了检测的难度，对数变换后的划痕图像对划痕缺陷区域的增强效果不明显，而经过PSO-Gabor滤波器处理后的划痕能量图的背景区域得到了抑制，缺陷区域得到了增强，增大了对比度。

(a)原图未处理

为了更加清楚地观察到3种增强方法对划痕图像的处理效果，图5列出了处理后划痕图像的水平灰度分布图，图中标示出缺陷区域所在像素位置，从图中可以看出，PSO-Gabor滤波处理后的能量图中缺陷区域和无缺陷区域的像素灰度值差异更大，表现为波峰更高、波谷更低，且低灰度区域灰度值趋于均衡。综合图4和图5可知，经PSO优化后的Gabor滤波器与缺陷图像卷积可以突出表面缺陷，增强缺陷与背景对比度，达到增强的效果。将能量图作为CNN的输入，可进一步实现钢板表面缺陷识别。

图5 3种增强方法处理后划痕水平灰度分布对比图

1.3 卷积神经网络结构的设计

CNN作为一种深度前馈人工神经网络，主要包括输入层、卷积层、池化层、全连接层和输出层，在图像识别、物体检测等领域得到广泛应用[18-19]。

本文设计的CNN模型由3个卷积层、2个池化层和1个全连接层组成。其中池化层采用最大值池化下采样，激活函数采用ReLU函数，输出层是一个6类别的Softmax分类器。输入图像先经过多层卷积层与池化层的运算，再通过全连接层转换为固定维度的特征向量，最后通过Softmax分类器得到该图像特征向量对应每种缺陷的概率，从而确定图像的缺陷种类。模型及参数信息如表2所示，其中F代表核矩阵大小，s代表步长，d代表卷积核个数。

表2 卷积神经网络的模型参数

2 实验测试与分析

2.1 缺陷图像数据集

本文选取东北大学的NEU-DET图像数据集[20]进行训练和测试，主要包含裂纹(Cr)、夹杂(In)、斑块(Pa)、麻点(Ps)、氧化铁皮压入(Rs)以及划痕(Sc)共6类缺陷，每类缺陷300张样本，共1 800张图片，样本图片的大小均为200 pixels×200 pixels。图6为部分样本图像。由图6可知，同一类别缺陷在形态、大小和光照均匀性等方面存在一定的差异性，而不同类别缺陷在形态方面相似度较高，如裂纹与氧化铁皮压入，夹杂与划痕。

图6 部分缺陷样本图像

为了提高模型的泛化能力，需先对图片数据集进行扩充[21]。考虑相机实时采集图像过程中最可能出现的情况，对原有图像数据集进行如下方式扩充：旋转90°、旋转180°、加高斯噪声、运动模糊处理，数据扩充后图像数据集增大到9 000张。

2.2 CNN网络模型的参数配置

将与Gabor滤波器卷积后得到的9 000张能量图作为CNN模型的输入进行模型训练与缺陷分类。将图像数据集按照3∶1∶1的比例划分为训练集(5 400张)、验证集(1 800张)和测试集(1 800张)3部分，其中训练集和验证集分别用于模型的训练和验证，测试集用于对模型进行性能评估。

从实验训练过程可知，当迭代次数为30时，模型分类准确率趋于稳定，因此将模型训练最大迭代次数设置为30。模型训练时，初始学习率较大使得网络模型中参数较快地逼近最优值，随着迭代次数增加，线性降低学习率可以使参数更容易逼近最优值[22]。如图7所示，本文研究不同初始学习率(1×10-4、3×10-4、5×10-4、7×10-4、1×10-3、3×10-3和5×10-3)和衰减模式(衰减因子γ=0.1，步长s=5，即表示学习率每迭代5次降低为上一次的10%)对模型分类准确率的影响。由图7可知，随着初始学习率增大，模型分类准确率呈现“先缓慢上升，后快速下降”的趋势，初始学习率为1×10-3时分类准确率最高，达到98.44%。因此，本文模型设置初始学习率为1×10-3，衰减因子γ=0.1，步长s=5。

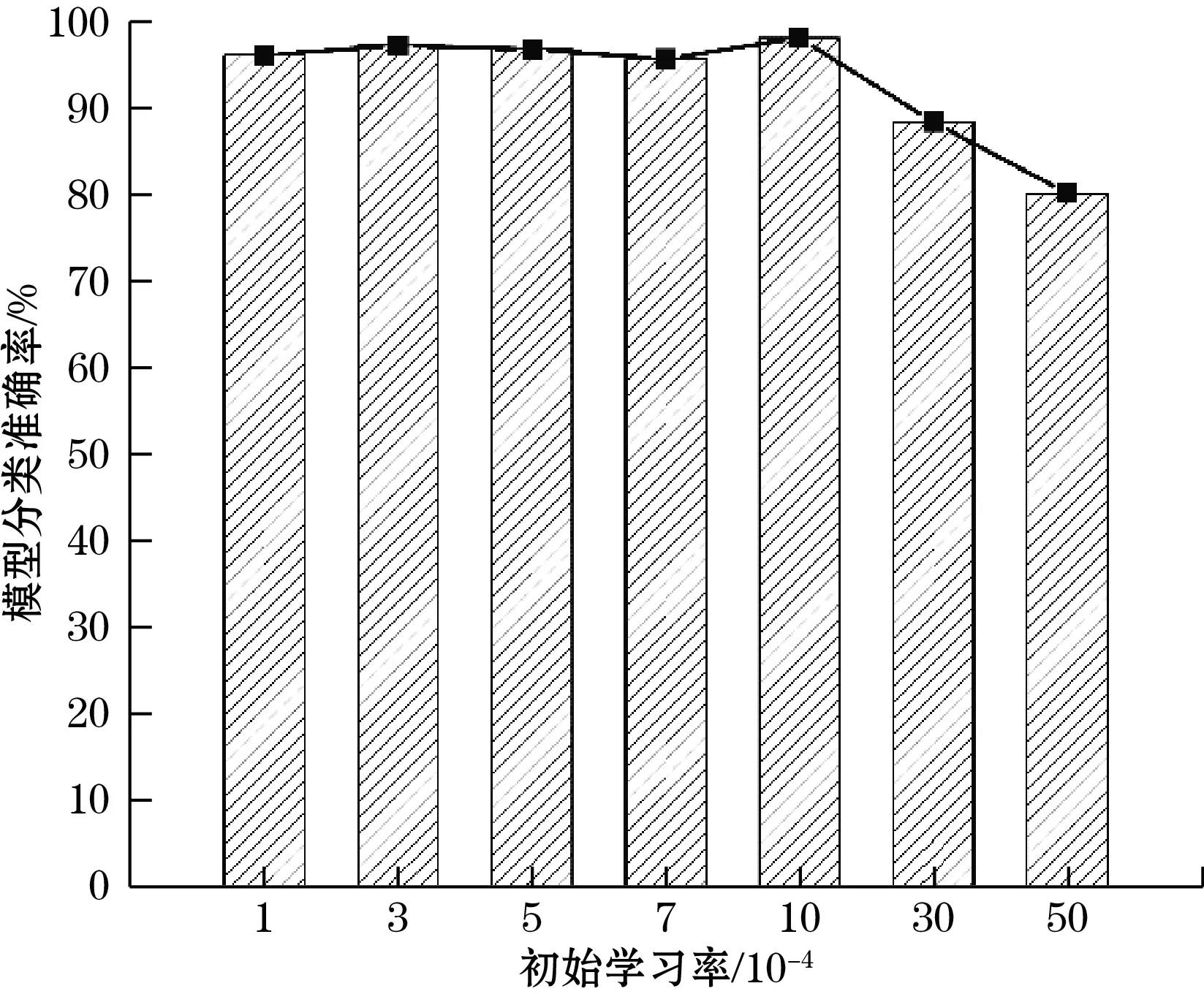
图7 不同初始学习率对分类准确率的影响

2.3 模型测试

以钢板表面6类缺陷，每类缺陷300张图像作为测试集对本文提出的基于PSO-Gabor特征增强的CNN网络模型(PSO-Gabor-CNN)的分类性能进行评估，每张图像测试时间约为50 ms。计算测试集混淆矩阵，结果如表3所示。

表3 测试集样本混淆矩阵

由测试集混淆矩阵计算该算法的分类准确率P、召回率R以及f。f综合了P和R的判断指标，f越大表示分类效果越好[23]，计算结果如表4所示。

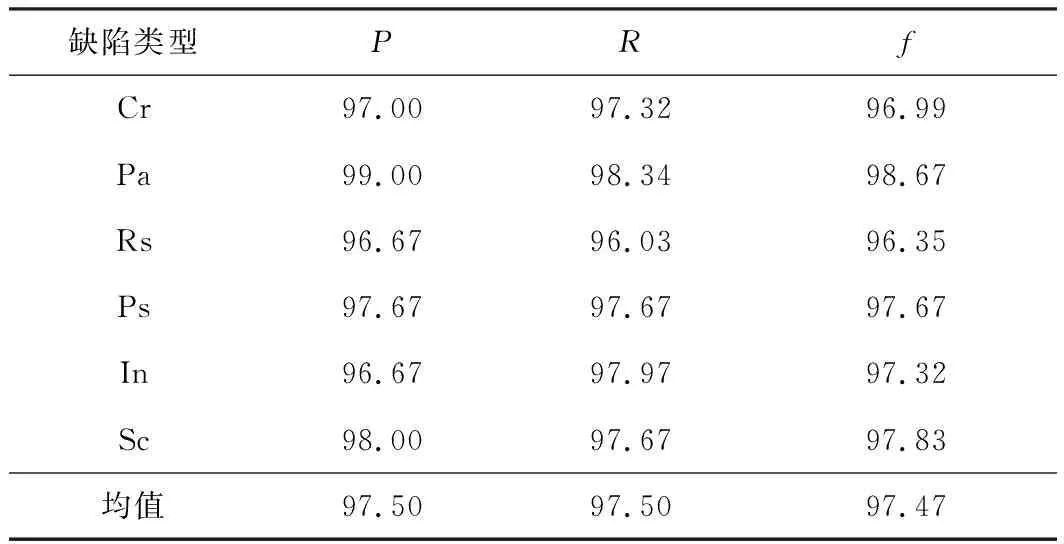
表4 网络模型性能评价指标 %

由表4可得，PSO-Gabor-CNN模型对6类缺陷的f平均值为97.47%，其中在斑块缺陷分类上表现最好，f达到98.67%；在氧化铁皮压入、裂纹缺陷分类上表现较差，f低于97.00%。其原因可能是由于氧化铁皮压入与裂纹在形态上相似，故两者易被误分，导致准确率较低。

2.4 模型比较

为了验证PSO-Gabor-CNN模型的有效性，分别从预处理方法与模型分类器方面进行对比。实验设计为：

(1)对比图像未经预处理、灰度对数变换预处理(LOG)、提取局部二值模式特征图像预处理(LBP)和PSO-Gabor预处理的CNN模型；

(2)对比基于PSO-Gabor预处理的反向传播神经网络(PSO-Gabor-BPNN)、支持向量机(PSO-Gabor-SVM)和卷积神经网络模型(PSO-Gabor-CNN)。

分别将训练集应用于上述方法进行模型训练，分类准确率与交叉熵随迭代次数变化曲线如图8所示。

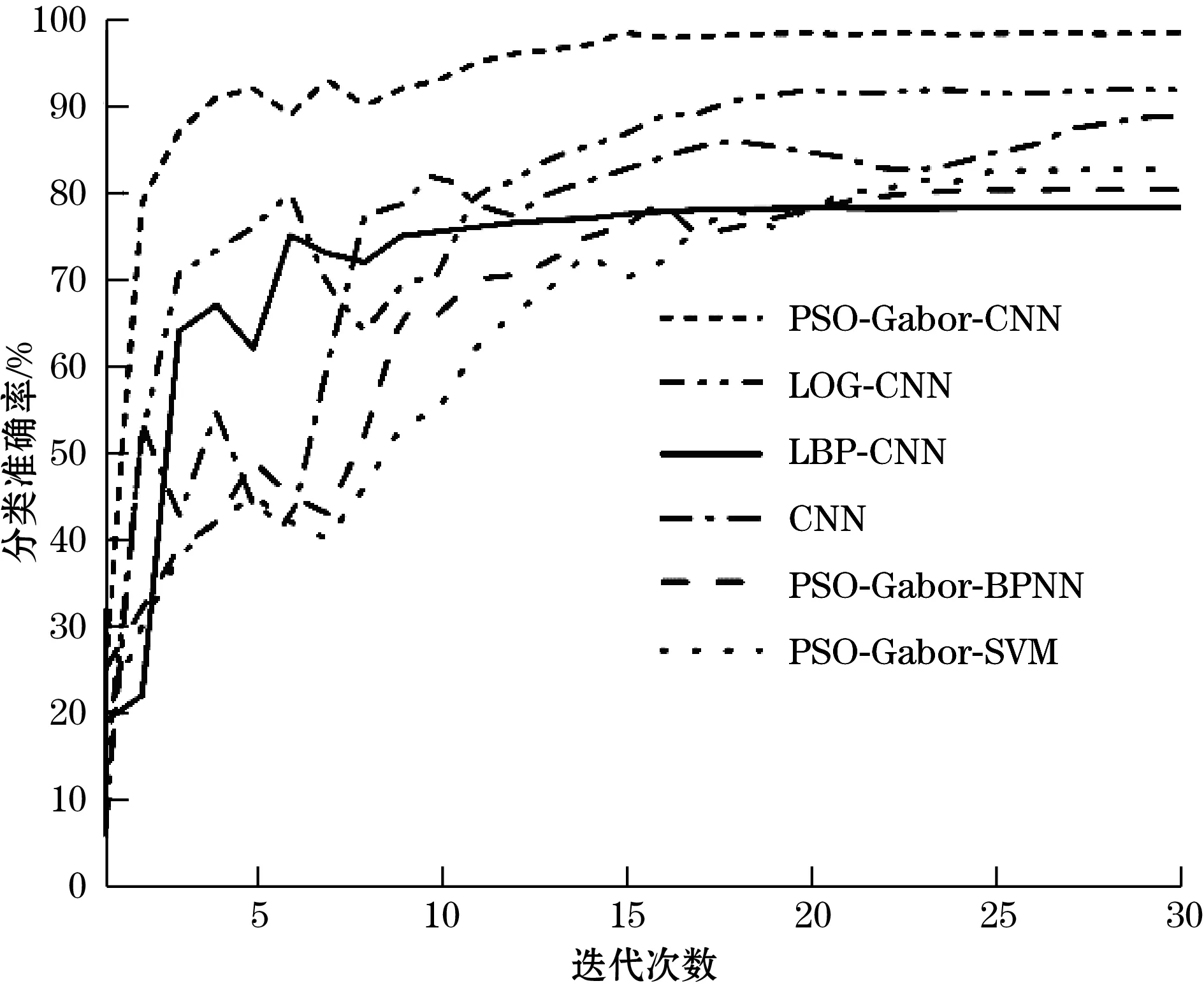
(a)分类准确率曲线

由图8可知，在模型训练过程中，CNN比BPNN和SVM更快收敛，且稳定性较高，尤其是基于PSO-Gabor-CNN的网络模型收敛速度最快，在第5代左右其分类准确率就达到90%以上，在15代左右其分类准确率稳定在98%以上；基于PSO-Gabor-SVM的网络模型收敛速度最慢，在训练次数达到25代以后其分类准确率逐渐稳定于82%。

表5给出了上述不同分类算法训练的交叉熵损失值与分类准确率稳定值。从表5可得，传统的模式识别算法BPNN和SVM分类准确率均小于85%，明显低于CNN模型分类准确率，交叉熵损失值也在1以上，明显大于CNN，模型分类效果差距较大。其原因可能是BPNN和SVM属于浅层分类器，对于提取钢板表面缺陷图像高维特征较困难，同时SVM分类器需要人工手动提取导致分类准确率偏低。另外，基于PSO-Gabor预处理方法较其他传统预处理算法可以显著提高CNN网络模型的分类准确率，文中PSO-Gabor-CNN网络模型的分类准确率与交叉熵损失值分别为98.44%和0.08，较未作预处理的CNN模型分类准确率提高11.77%，交叉熵降低0.90；较基于LBP特征提取的CNN模型分类准确率提升了20.22%，交叉熵降低1.77。综上所述，本文提出的基于PSO-Gabor-CNN网络模型分类准确率高，分类效果好。

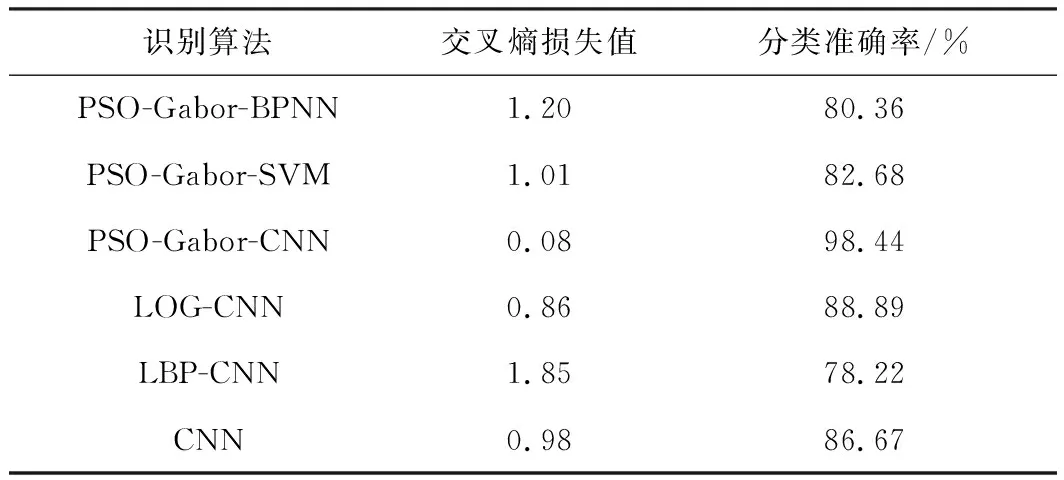
表5 不同识别算法性能对比效果

3 结束语

为了解决工业生产中钢板表面缺陷的类内缺陷形态差异大、类间缺陷相似度高且识别准确率较低的问题，本文提出了基于PSO-Gabor特征增强的钢板表面缺陷识别方法。首先研究了Gabor滤波器的频率φ、方向θ、尺度σ以及滤波窗口尺寸W对Gabor滤波器滤波性能的影响；然后采用PSO算法优化Gabor滤波器的4个决定性参数，并获得Gabor滤波器的最优参数分别为：φ=4.48、θ=3π/4、σ=1.5、W=31，根据最优参数构造Gabor滤波器并与钢板表面缺陷图像进行卷积操作，计算其能量响应值获得对应的缺陷能量图；针对滤波后的缺陷能量图设计卷积神经网络模型，最终模型的缺陷分类准确率达到97.5%，识别时间约为50 ms，极大地提升了缺陷分类识别的能力；并通过缺陷分类识别实例及对比实验验证了本文方法的有效性。本文对钢板表面的6类常见缺陷进行检测与识别，后期研究可扩大缺陷种类，进一步完善分类模型。