基于单目视觉的光电跟踪传感器设计

兰建军

(福建水利电力职业技术学院电力工程学院，福建永安 366000)

0 引言

由于受光伏组件现有发电效率的制约，提高光伏发电效率的研究热点主要聚焦在光电跟踪和最大功率点跟踪方面[1]。在光电跟踪方面，主要采用主动式、被动式和混合式方案，主动式跟踪依据视日运动轨迹进行跟踪，其跟踪精度低，通常用于粗跟踪，因此被动式跟踪成为光电跟踪的研究重点[2]。被动式跟踪方案中较多利用光敏电阻或光敏晶体管等器件实现[3-5]，为了实现双轴跟踪，王正、王海澜、赵卫东等利用隔板对光敏电阻进行了四象限布局改进后实现了双轴跟踪[6-8]，为进一步提高跟踪的范围和精度，宁宇等又提出了光敏器件的六象限布局改进方案[9]。尽管在光敏器件布局上进行了改进，但上述光敏器件仍然是离散分布，难以实现连续的高精度跟踪。为解决离散分布问题，曲春英等提出一种基于PSD的检测方案，在实现连续检测的同时，将检测精度提升至0.2°[10]。柯熙政、H. J. Kim等又先后提出了基于质心算法的图像检测方案，方案中太阳光直接照射摄像头，摄像头图像容易受背景杂光影响，因此检测精度只能提升至0.1°左右[11-12]。

本文设计了一种新型的传感器结构，传感器利用入射面上的环形光缝将太阳光线引入传感器投影面后形成圆形光环，利用单目视觉检测方式测量光环的中心坐标后，实现太阳的方位角和高度角测量。针对光环成像椭圆化的问题，利用椭圆的几何特征方法对Hough变换椭圆识别算法进行了改进，最后利用设计标定实验板对传感器进行了实验测试，给出了实验测试数据，实验结果表明本传感器方案方位角检测精度可达0.05°。

1 传感器结构与原理

1.1 传感器结构

图1为传感器结构示意图，参照图1(a)，其外形结构为不透光的密闭圆柱形容器，容器的顶部和底部设置有光线入射面和光线投影面，二者相互平行。光线入射面上的圆环形透光缝可将光线导入密闭容器，并在底部的投影面上生成圆形光环。入射面底部的摄像头用于检测圆形光环的中心坐标。太阳光线垂直照射时，投影面上的光环处于投影面中心位置；光线斜射时，光环将偏离投影面中心，计算出光环中心位置后实现太阳方位角和高度角的测量。参照图1(b)可知，以投影面为参考面，入射面高度为H，摄像头高度为H1。入射面为不透光的钛合金圆盘，圆盘厚度n、直径D1，光缝外径D2、宽度d，摄像头安装于圆盘中心处。

(a)整体结构图(b)剖面图图1 传感器结构示意图

1.2 工作原理与分析

图2为针孔成像模型示意图，Ow—XwYwZw为世界坐标系，Oc—XcYcZc为相机坐标系，Op—XpYpZp为图像坐标系，O—UV表示像素坐标系。Oc为相机光心(相机坐标系原点)，OcZc为相机光轴。设p为世界坐标系中的点，p点在相机坐标系和世界坐标系的坐标分别为(Xc，Yc，Zc)和(Xw，Yw，Zw)，p点的像点p′在图像坐标系和像素坐标系中的坐标分别为(x，y)和(u，v)。

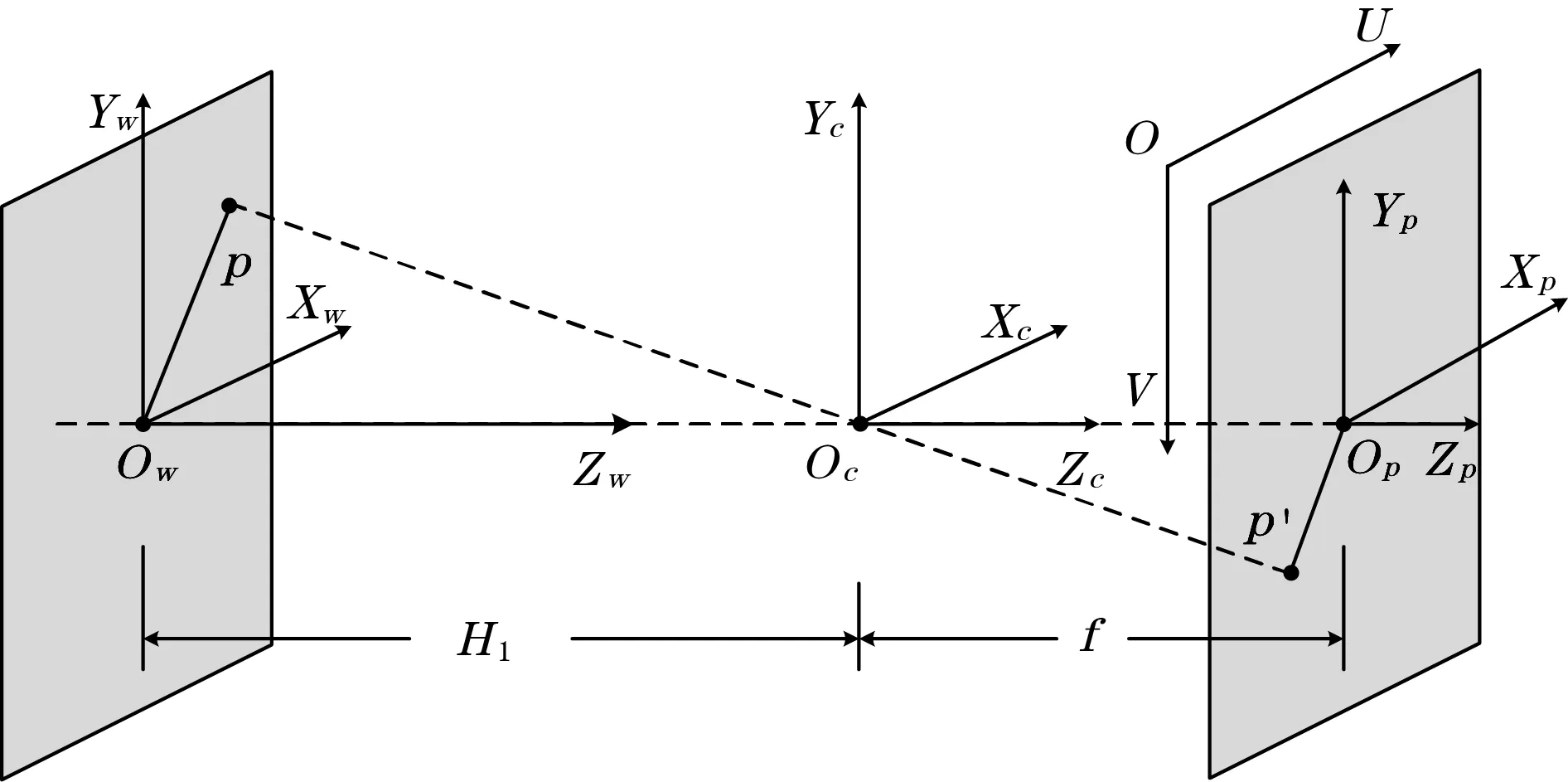
图2 针孔成像模型示意图

根据光孔成像模型三次坐标变换关系可知[13]，世界坐标系和相机坐标系的关系可通过如式(1)所示旋转矩阵和平移矩阵描述。

(1)

式中：R、T分别为旋转矩阵和平移矩阵，也称为摄像头外参数。

相机坐标系和图像坐标系之间的转换关系如式(2)所示：

(2)

式中：f为摄像头焦距；dx和dy分别为摄像头在x和y方向的像元尺寸，也称为摄像头内参数；u0、v0分别为摄像头光心在像素坐标系中的坐标。

图像坐标系和像素坐标系在同一个平面中，只是二者度量单位和坐标原点不同。图像坐标系原点Op为摄像头光轴和像平面的交点，位于像平面中心，二者关系可以通过式(3)表示。

(3)

图3所示为方位角和高度角计算原理示意图，当入射光线由垂直照射变成斜射时，假设圆环中心从B点移动至C点，根据C点坐标(x，y)即可通过式(4)完成方位角和高度角测量。

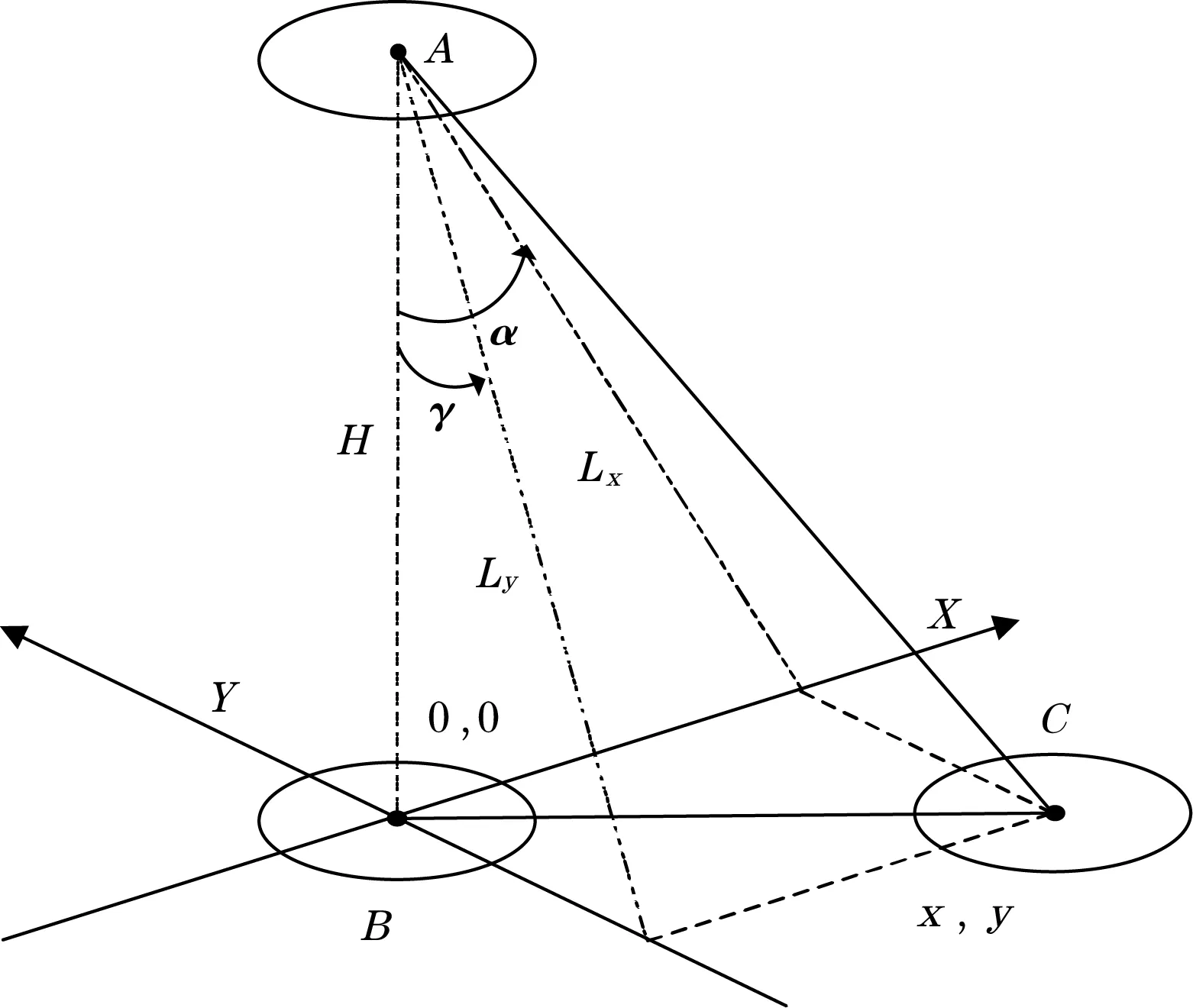
图3 方位角和高度角计算原理示意图

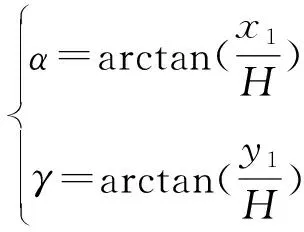
(4)

式中：H为入射面和投影面之间的距离；α为方位角；γ为高度角。

2 传感器标定测试

2.1 传感器参数确定

摄像头选择OV5640，其像元尺寸1.4 μm×1.4 μm，最高分辨率2 592 pixel×1 944 pixel，焦距配置为手动调节模式。测试时，在投影面上铺设了同心圆环刻度坐标，打开入射面底部的微弱光源。调节摄像头的位置和焦距，保证摄像头准确聚焦的同时，让摄像头宽度视场尽可能接近100 mm，图4所示为传感器样机安装调节后的测试图像，调试完成后的传感器尺寸参数如表1所示。

图4 传感器测试图像

表1 传感器尺寸参数表 mm

2.2 理论计算与参数标定

依据传感器测试图像的分辨率和宽度视场信息，在不考虑图像畸变时，图像测量的分辨率为100 mm/1 944=0.051 mm，代入式(4)，可计算出传感器的理论检测精度为0.033°。同时，根据式(5)所示的相机焦距计算公式，式(2)中的摄像头焦距f标定结果为2.18 mm。

f=(P·D)/W

(5)

式中：P为像宽(像素宽度×像元尺寸)，P=2 721 μm；W为实际物体宽度(图像高度视场)，W=100.0 mm；D为物距，D=80.0 mm。

由于入射面、投影面和摄像头镜面平行，即物体平面、摄像头平面和像平面平行，且OcZc同时通过世界坐标系原点Ow和像素坐标系原点Op，不存在旋转关系，并且物距长度H1固定，故式(1)中的R、T矩阵均可忽略。

3 实验测试与数据分析

3.1 图像预处理

由于传感器为密闭不透光容器，因此拍摄的图像受环境光线影响较小，简单的背景分割后就可进行边缘检测。对图像进行灰度变换、二值分割、形态学滤波和边缘提取等图像预处理过程后，就可以利用相应算法进行光环检测，图5所示为各环节图像预处理后的效果图。

(a)转灰度处理

3.2 Hough变换椭圆检测

当投影面上的光环偏离投影面中心时，圆环中心和透镜光轴存在一定夹角，光环在成像过程中存在椭圆化问题[14]，因此对光环图像边缘检测需采用椭圆曲线方案。另外，尽管光环图像背景简单，但光环边缘存在噪声，为了精确求解图像边缘椭圆曲线的相应参数，选用鲁棒性好、精度高的Hough变换图像曲线检测方案。

基本Hough变换椭圆拟合思路是将式(6)所示的椭圆旋转一般参数方程映射到图像边缘点集中，将图像边缘点集中的任意点(xk，yk)看作常量，遍历点集中的每组(a，b，p，q)参数，满足式(7)条件后参数累加器加1，参数累加器中最大值对应的参数(a，b，p，q)就是最优参数[15]。

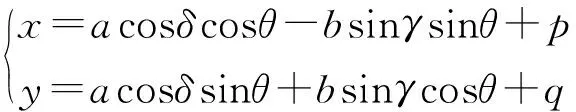
(6)

式中：δ为圆心角；θ为旋转角；p、q为椭圆中心坐标；a、b分别为椭圆短轴和长轴。

(7)

3.3 改进Hough变换算法

基本Hough变换进行多到一的映射后将生成多维空间，运算量巨大。根据椭圆几何特征可知，椭圆的短轴是平面上所有点到椭圆边界上点的最大距离的最小值。利用椭圆几何特征，可将多维空间降低为二维空间，改进后的Hough变换椭圆检测算法流程如图6所示。

图6 改进Hough算法流程

图7为改进的Hough变换算法进行椭圆识别的输出图，图中正方形区域为椭圆中心，像素坐标(1 374 pixel，1 551 pixel)，短轴和长轴像素长度分别为a=202 pixel，b=208 pixel，原始图像外围的轮廓为拟合的椭圆曲线。依据椭圆中心像素坐标，联立式(1)～式(4)后可求解光环位置对应的方位角和高度角。

图7 Hough变换结果输出图

3.4 实验数据与分析

为验证传感器的实际测量精度，传统方式是将传感器固定在可二维旋转的云台上进行标定测试。但由于太阳光线角度时刻变化，加之传感器固定平台也存在误差，因此选用图板标定方案对传感器进行标定测试，设计了如图8所示的9张白色背景标定测试板，圆环为黑色，直径、宽度和实际太阳光环大小相同。相邻测试板的圆心坐标在X和Y轴方向上的间隔均为5 mm，测试数据如表2所示。

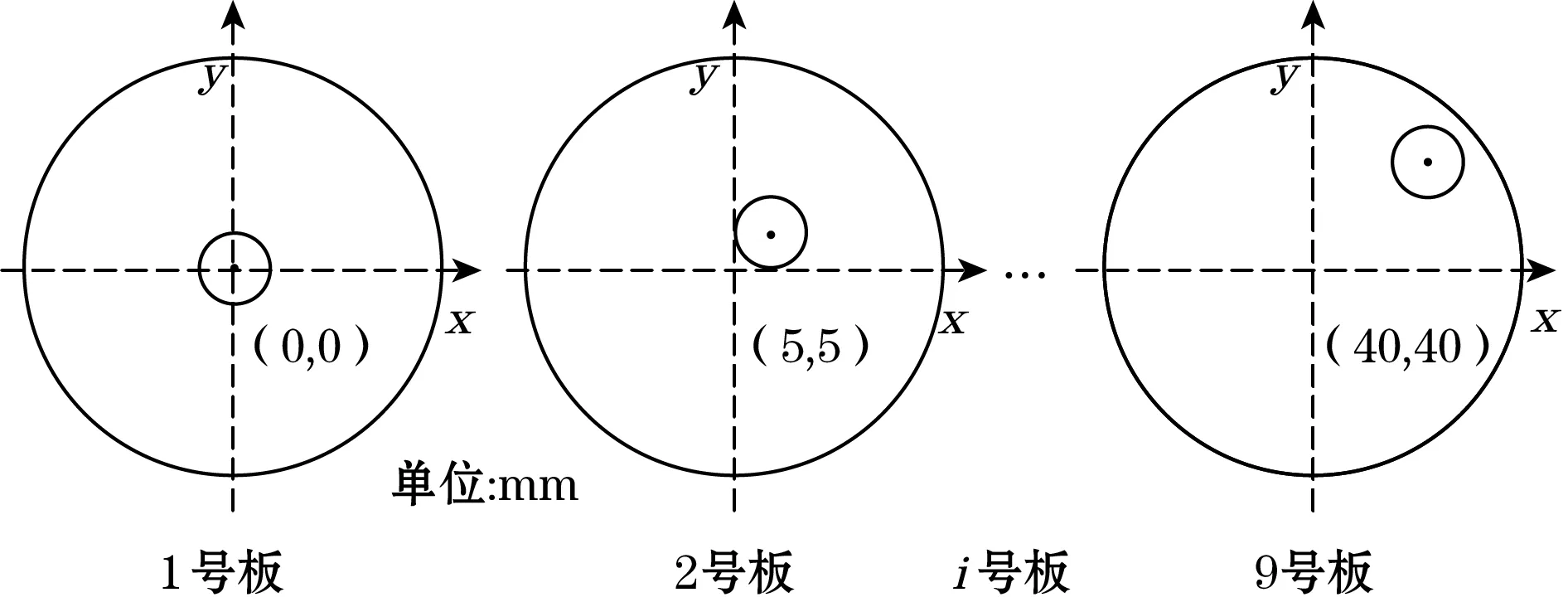
图8 白色背景标定板示意图

表2 测量数据及误差分析表 (°)

4 结论

本文设计的光电跟踪传感器利用镂空圆形缝隙将光线导入传感器投影面，通过摄像头捕捉光环图像后，经图像处理完成光环中心坐标测量，方位角和高度角的测量精度为0.05°，可应用光伏发电等场合的太阳跟踪。