一种模态局部化压力传感器的设计与仿真
2022-09-26曾一笑
康 昊,曾一笑
(1.西安近代化学研究所,陕西西安 710065;2.成都凯天电子股份有限公司,四川成都 610000)
0 引言
基于MEMS 技术的谐振式压力传感器具有体积小、质量轻、功耗低、与集成电路工艺兼容、易于大批量生产、抗干扰能力强以及稳定性高等优点[1]。其具有较高的检测精度,适合远距离传输,并且信息采集与处理更加便捷。同时由于其与集成电路工艺兼容,可应用于高精度的智能化测控系统。因此,基于MEMS技术的谐振式压力传感器在航空航天技术领域,尤其在人造卫星、飞机导航、飞行控制、飞行器、机载大气数据系统、飞行参数记录仪等方面,以及爆炸场中准静态压力的测量具有重要的作用[2]。
基于MEMS技术的谐振式压力传感器是国内外研究单位的研究热点,并且取得了研究成果,改善了谐振式压力传感器的灵敏度、非线性等性能指标[3-8]。但是,基于现有微机械加工的条件和结构设计,谐振式压力传感器灵敏度等性能指标很难得到明显改善。近年来,模态局部化效应被应用于各种谐振式传感器[9-16],并被证明具有超高的灵敏度和良好的环境适应性。模态局部化现象由P. W. Anderson[17]在固态物理中发现。对于谐调系统其振动能量均匀分布于整个结构,若系统的参数存在失调,很小的失调量就会使系统中的能量分布发生变化,能量将集中于系统的某个区域,这就是模态局部化现象[18-22]。因此,多自由度谐振器系统中微弱的质量或者刚度的变化将会使得该系统发生模态局部化现象,从而极大提高了谐振式传感器的灵敏度。本文将模态局部化现象应用于谐振式压力传感器,提出一种基于二自由度谐振器系统的压力传感器,对传感器进行了理论和仿真分析,利用幅值比作为输出,仿真结果表明基于幅值比的输出灵敏度相比频率输出得到了大幅的提高。
1 传感器结构设计与理论分析
1.1 传感器结构设计
本文提出的基于二自由度谐振器的模态局部化压力传感器的结构截面图如图1(a)所示,传感器基于SOI(silicon on insulator)硅片制备。传感器由敏感膜片和二自由度谐振器系统组成,敏感膜片用于直接感知外界待测压力,二自由度谐振器系统中的一个谐振器通过2个锚点分别固定于2个敏感膜片,另一个谐振器通过2个锚点固定于硅基底。
二自由度谐振器系统的结构示意图如图1(b)所示,二自由度谐振器系统由2个谐振器组成,2个谐振器结构相同,通过耦合结构连接,每个谐振器设计有驱动梳齿用于驱动谐振器,使谐振器处于谐振状态。在每个谐振器谐振梁的一侧设计有调谐电极,用于改变谐振器的有效刚度。每个谐振器设计有平板电容用于检测谐振器的振幅信号。

(a)传感器结构截面图
本文提出的基于二自由度谐振器的模态局部化压力传感器的结构设计参数如表1所示。
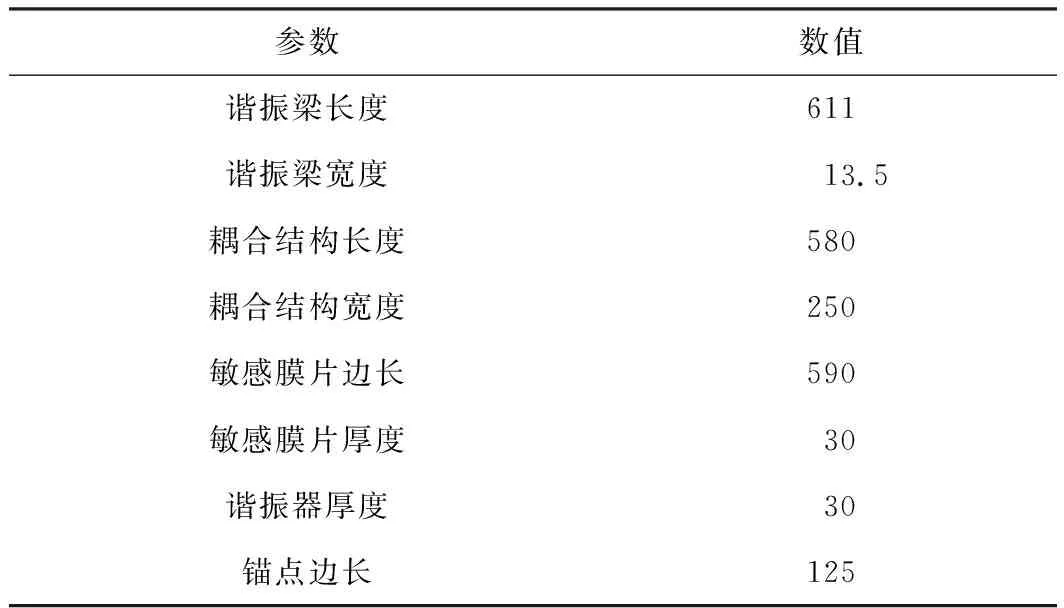
表1 传感器结构设计参数 μm
1.2 传感器工作原理
当给驱动电极和谐振器分别施加交流电压和直流偏置电压时,谐振器系统在谐振频率处振动。在理想情况下,即2个谐振器的结构参数完全相同,2个谐振器的振幅是相等的。当外界压力作用于敏感膜片时,敏感膜片会发生变形,在垂直于敏感膜片的z轴会产生位移,导致位于敏感膜片上的锚点发生偏转,如图2所示,从而使得锚点在y轴方向,即谐振器的轴向,会产生位移,相当于力载荷在轴向作用于锚点,改变了谐振器的刚度。由于只有一个谐振器的锚点位于敏感膜片上方,因此其中一个谐振器的刚度改变相当于对谐振器系统引入了一个刚度扰动,导致2个谐振器的参数发生失调,从而使得该谐振器系统产生模态局部化效应,使振动能量不在2个谐振器均匀分布,最终表现为2个谐振器振幅的不相等。因此,通过检测谐振器的振幅比可以获得输入压力的大小。

图2 敏感膜片变形下的锚点偏转
1.3 敏感膜片理论分析
本文中设计的敏感膜片为方形,属于薄板。板的平面尺寸与厚度之比在5~80之内的称为薄板,小于5的称为厚板,大于80的称为薄膜。方形膜片的谐振频率可由式(1)计算。
(1)
式中:t为膜片厚度;a为膜片的宽度;E为弹性模量;ρ为材料的密度;ν为泊松比。
文中敏感膜片受压时的变形是基于薄板的小挠度变形理论。薄板小挠度变形理论是指薄板受到垂直于板面的压力载荷后,薄板的最大形变不大于板厚度的1/5。压力施加到敏感膜片上时,其变形呈抛物线形状,膜片不同位置处的挠度为
(2)
式中:x、y为以膜片中心点为0点坐标系中的横、纵坐标;2a为膜片的边长;d0为膜片中心处的挠度。
膜片为四边固支,因此在膜片的边缘处,即x=±a,y=±a时,膜片的形变为0,而在膜片的中心点处(x=0,y=0)的变形最大,该点的挠度d0为
(3)
式中p为施加于敏感膜片的压力载荷。
在x和y方向的应力分别为
(4)
为了使传感器获得较大的灵敏度,应增大敏感膜片变形时谐振器锚点的偏转,并且应处于应力最小的区域。由分析可知,从膜片边缘至中心处变形从0逐渐增大、应力从最大逐渐减小。因此,将锚点的中心布设于膜片中心点与边缘间的中心处(即x=0,y=±0.5a),如图3所示。

图3 锚点位置示意图
1.4 谐振器理论分析
二自由度谐振器系统可等效为质量-刚度-阻尼模型,如图4所示。在该模型中,2个谐振器的初始参数相同,质量、刚度、阻尼分别为m、k、c,振动位移分别为x1、x2,谐振器之间的耦合刚度为kc,由于谐振器在真空环境下工作,忽略其阻尼,假设其中一个谐振器的刚度因敏感膜片的变形发生Δk的刚度变化,此时二自由度谐振器系统的自由振动方程可由式(5)表示。

图4 二自由度谐振器等效模型
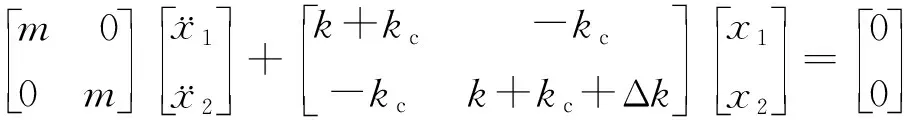
(5)
求该动态微分方程的特征值和特征向量,可以得到二自由度谐振器在一、二阶模态的谐振频率和幅值比分别为:
(6)
(7)
因此,基于频率和幅值比输出的灵敏度分别为:
(8)
(9)
由式(8)和式(9)可以得出,基于幅值比输出的灵敏度相比频率输出提升:
(10)
因此,当耦合刚度kc远小于谐振器刚度k时,基于幅值比输出的灵敏度相比频率输出可获得大幅的提升。
2 传感器仿真分析
本文利用COMSOL有限元软件对基于二自由度谐振器的模态局部化压力传感器进行了仿真分析,包括二自由度谐振器系统的模态分析、敏感膜片的静态载荷分析以及传感器的灵敏度分析。
2.1 仿真模型及方法
基于二自由度谐振器的模态局部化压力传感器的仿真模型如图5所示。为了保证仿真的准确性,仿真模型为全对称结构,包含了4个膜片和2自由度谐振器系统,为了简化仿真模型,模型中忽略了驱动梳齿和平板电容,将两部分的质量与谐振器质量进行了等效以保证仿真的准确性,仿真模型的结构参数如表1所示。对4个膜片的4个侧边施加固定约束,对敏感膜片1、2施加z方向的静态载荷压力,用于对其中一个谐振器施加刚度扰动,最后通过“稳态”和“特征频率”研究模块对二自由度谐振器系统的模态进行求解,可得到谐振器各阶模态的谐振频率和振型。

图5 压力传感器仿真模型
2.2 模态分析
二自由度谐振器的初始振动模态如图6 所示,在第1阶模态,2个谐振器在相同方向运动,一阶模态称为同相模态;在第2阶模态,2个谐振器在相反方向运动,二阶模态称为反相模态。由于谐振器不受载荷作用,2个谐振器的结构参数完全相同,因此两谐振器在前两阶模态的振幅相等,一阶模态的谐振频率为58 443.552 Hz,二阶模态的谐振频率为58 735.058 Hz,频差为291.506 Hz。

(a)同相模态
2.3 静态载荷分析
对谐振器1所固定的2个锚点所在的敏感膜片在z轴方向施加了2 MPa的压力载荷,应力和位移分布图如图7所示。敏感膜片位移分布图如图7(a)所示,敏感膜片中心处位移达到最大值,最大位移为0.79 μm,仅为敏感膜片厚度的2.63%,符合薄板变形理论的条件;敏感膜片应力分布图如图7(b)所示,敏感膜片四边边缘中心处应力最大,在膜片中心处应力最小,与理论分析一致,应力最大值为212.01 MPa,远小于硅材料的断裂强度。因此,传感器可在2 MPa的压力载荷下正常工作。
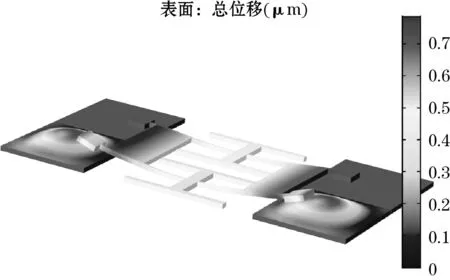
(a)位移分布
2.4 灵敏度分析
对传感器在0~2 MPa载荷内的频率和幅值输出进行了仿真,仿真结果如图8所示。由图7(b)可以看出,当压力载荷施加于敏感膜片时,锚点向内偏转,相当于锚点受到了压应力,即谐振器在压力的作用下产生了收缩,谐振器的刚度变小,使得谐振器在压力的作用下频率减小。根据图8,基于频率输出的灵敏度为2 221.8 Hz/MPa;基于幅值比输出的灵敏度为17.952/MPa。由于幅值比为无量纲输出,为了与频率(Hz)在同一尺度进行比较,得到了基于频率和幅值比输出的相对变化,如图9所示,基于频率输出的相对灵敏度为0.038 ppm/MPa,基于幅值比输出的相对灵敏度为17.998 ppm/MPa,为频率输出的473.6倍。1 ppm=10-6。
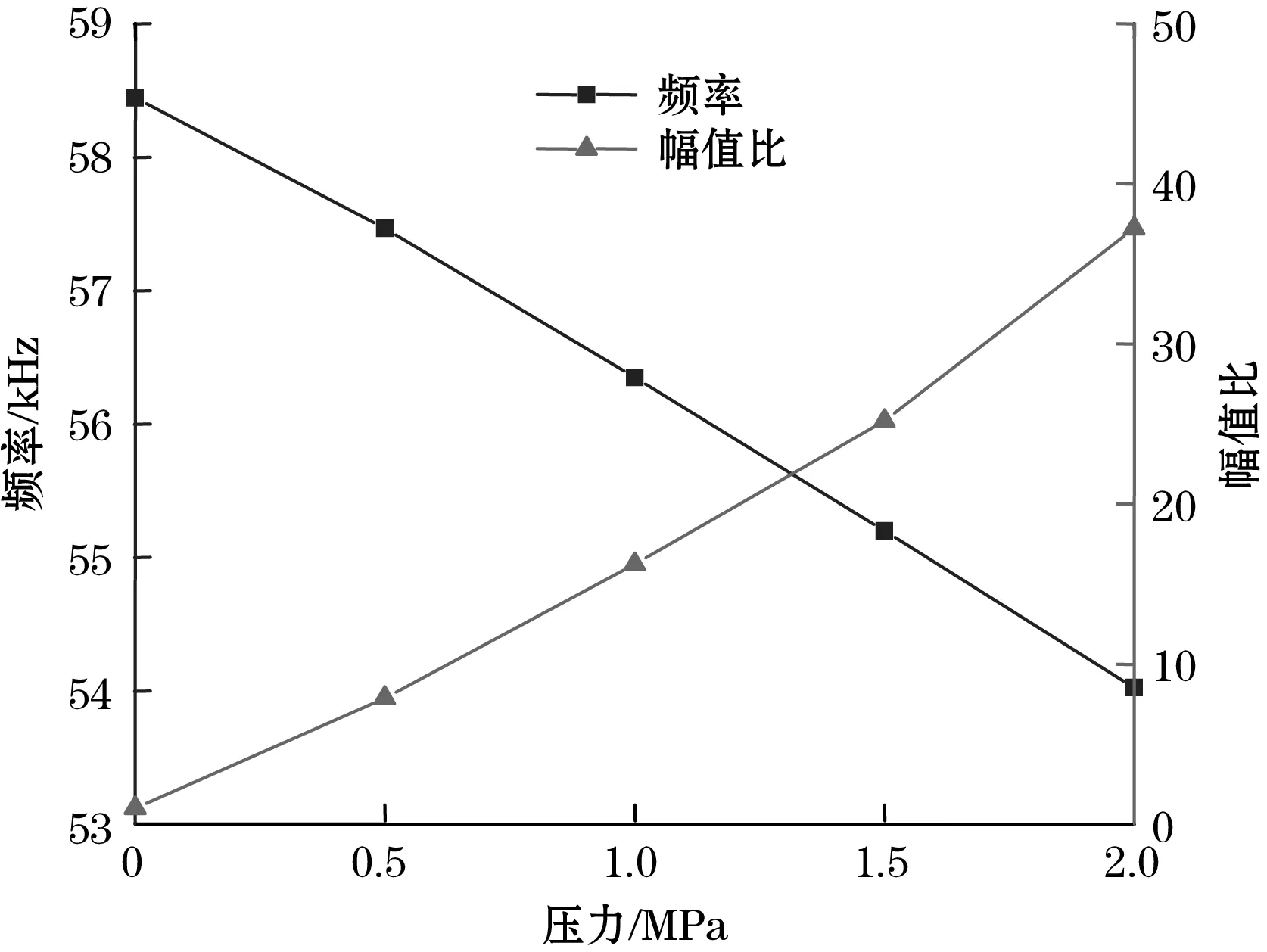
图8 幅值比和频率输出

图9 幅值比和频率相对变化
3 结束语
本文提出了一种基于二自由度谐振器的压力传感器,将模态局部化效应应用于谐振式压力传感器。本文对传感器的敏感膜片和二自由度谐振器进行了理论分析,利用COMSOL有限元软件对传感器的静态载荷和模态振型进行了分析。仿真结果表明,传感器可在2 MPa压力载荷范围内正常工作,基于幅值比输出的灵敏度为频率输出的473.6倍。本文提出的模态局部化压力传感器为进一步改善谐振式压力传感器的性能提供了途径。
