基于ANSYS的润滑油路静电传感器建模与仿真特性分析

谷 猛,刘若晨,贝绍轶,孙见忠

(1.江苏理工学院汽车与交通工程学院，江苏常州 213001;2.南京航空航天大学民航学院，江苏南京 211106)

0 引言

基于静电感应原理和荷电机理的静电监测技术已在国内外的航空发动机气路监测中应用[1-2]。BOOTH、HARVEY等对油液磨损静电监测的研究表明静电监测技术也可运用于油路[3-4]。对于润滑油路静电传感器的理论研究，黄文杰、陈志雄等通过建立点电荷感应数学模型进行传感器分析[5-6]，刘若晨等运用润滑油路静电传感器数学模型对特性参数进行分析[7-9]。但使用数学模型进行计算的过程中需要运用大量的公式比较繁琐且难以对一些器件材料和工作环境进行考虑，导致所得结果可能会出现误差。为了解决理论研究存在的一些弊端，仿真的实验方法开始广泛运用。孙见忠等提出了一种使用ANSYS软件来对航空发动机砂尘吸入物静电监测的仿真实验方法[10-11]；殷逸冰等采用有限元分析工具对环式静电传感器空感应情况进行仿真[12]；白杰等应用ANSYS来计算静电传感器的空间感应电势和电场[13]。本文结合润滑油路静电传感器的结构特点，采用ANSYS进行有限元建模，并对其特性参数空间灵敏度和传感器效率进行仿真计算和分析，验证该方法用于静电传感器特性研究的适用性和准确性。

1 润滑油路静电监测原理

润滑油路静电传感器(oil-line sensor，OLS)一般用来对流经传感器内部的润滑油所携带的带电颗粒进行监测。机械系统摩擦磨损会产生大量的带电颗粒，因此将静电传感器安装在循环润滑油路中，当润滑油中的带电颗粒经过传感器探极感应面时，电场线将集中指向探极感应面，探极的近端会产生相反电位的电荷，将相同电位的电荷驱赶到探极表面的远端，输出监测到的电荷信号。OLS监测示意图如图1所示。

图1 静电传感器监测示意图

OLS的结构示意图与实物图分别如图2、图3所示，主要由用来对润滑油中带电颗粒进行监测的探极感应面；用来防止电荷外泄保证感应电荷可靠性的绝缘层；用来将探极与外界隔离防止监测时外界干扰影响的屏蔽层等部分组成。其中传感器的两端采用法兰将传感器与管道连接起来，使油液能够流通到传感器的内部，微型接触器用来对监测到的静电信号进行输出。

图2 OLS结构示意图

图3 OLS实物图

2 静电传感器有限元模型建立

2.1 模型建立与参数设置

根据有限元法建立的理论数学模型中OLS产生的静电场满足的条件方程如下：

(1)

式中：φ(x,y,z)为静电场中的电势分布；ε0为真空介电常数；ρ(x,y,z)为静电场内的电荷密度分布；Γp、Γi、Γt分别为探极、绝缘层、屏蔽层的边界；σ(x,y,z)为探极感应的电荷密度；E(x,y,z)为静电场中生成的电场强度。

由静电场理论与高斯定理可知感应电荷量Q为

(2)

式中：S为传感器的表面积；D(x,y,z)为传感器表面上的磁通量分布；dS为面积微元。

运用式(2)直接对传感器上所产生的感应电荷量进行计算存在困难，所以采用有限元仿真进行计算。

对于三维静电场有限元分析，结合OLS的结构尺寸和形状，单元类型选用solid122单元，所建模型如图4所示。管道长度设置为100 mm，管道壁内径与感应电极直径一致均设置为20 mm，感应电极的初始长度尺寸设置为10 mm。仿真模型各部分的材质设置情况如表1所示。

图4 简化仿真模型

表1 材质选用

2.2 网格划分与激励施加

采用映射网格对OLS模型进行网格划分，通道单元每隔1 mm进行一次划分，并对传感器进行必要的细化，可以满足实际的高精度需求。考虑到传感器的实际使用情况，防止感应面感应到的静电信号受到外界电场的影响，传感器屏蔽层和通道都是接地的，因此需要给通道和屏蔽层施加0 V的电势，且由于探极感应面为等势面，因此需要将感应面的节点进行耦合，使其电势相等。网格划分和激励施加效果图如图5所示。

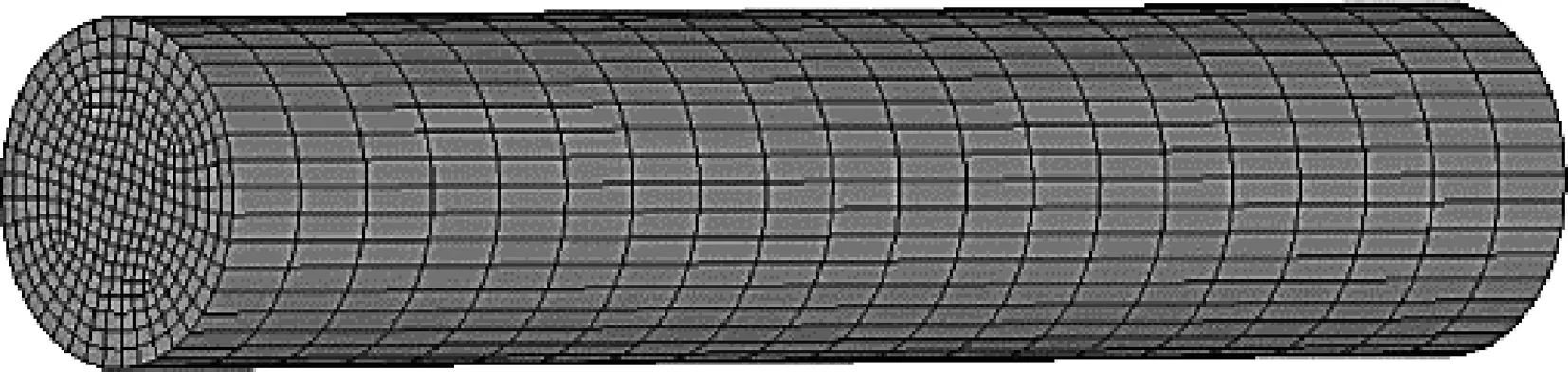
(a)网格划分

ANSYS中，在不设置的情况下，系统一般默认使用波前求解器，由于本文的仿真模型并不复杂，因此采用波前求解器就能够求解出在点电荷下感应面的感应电势，但实际需要的是探极感应面在点电荷下所感应的电荷量，而其只与垂直于感应面的电场强度有关，因此在计算感应电荷量时，还需要先提取垂直感应面的电场强度来计算探极上的感应电荷量。

3 静电传感器有限元仿真结果分析

3.1 空间灵敏度特性

基于静电感应原理，点电荷在管道内的位置不同时，产生的静电场也不相同，导致静电传感器所感应的电荷量改变，为了清晰地反映OLS在空间上所感应的电荷量随点电荷在空间位置变化的规律，引入空间灵敏度作为性能参数指标。理论公式如下：

s=|Q/q|

(3)

式中：s为传感器的空间灵敏度；q和Q分别为点电荷自身的带电量和探极在点电荷下产生的感应电量。

对于OLS空间灵敏度特性的研究主要集中在以下2个方面：探极尺寸不变的情况下，改变施感电荷在管道中的径向和轴向位置观察空间灵敏度的分布规律；探极尺寸变化的情况下分析施感电荷在管道中同一径向位置在不同轴向上的空间灵敏度分布规律。

根据初始设定探极直径D=20 mm，长度H=10 mm进行仿真后的传感器空间灵敏度分布结果如图6所示。

(a)不同径向位置灵敏度沿轴向的分布

从图6(a)可以看出，径向位置固定，随着|z|的减小，灵敏度不断增大，并在z=0处的灵敏度达到最大，即点电荷位于探极的中心的横截面上时，灵敏度最大。从图6(b)看出，轴向位置固定，当|z|<5即点电荷位于探极的内部时，灵敏度随着|z|的减少而减小，即点电荷越接近探极中心轴线时，灵敏度越小，并在中心轴线x=0处达到最小。而当|z|>5即点电荷位于探极的外部时，灵敏度随着|x|的减少而增大，即点电荷越接近探极的中心轴线时，灵敏度越大，并在探极中心轴线x=0处达到最大。

对于探极尺寸变化的空间灵敏度研究主要是固定探极长度或直径观察另一参数的变化对空间灵敏度的影响。分别对探极长度和直径参数进行设定，得出点电荷在同一径向位置x=0处仿真后的灵敏度分布如图7所示。

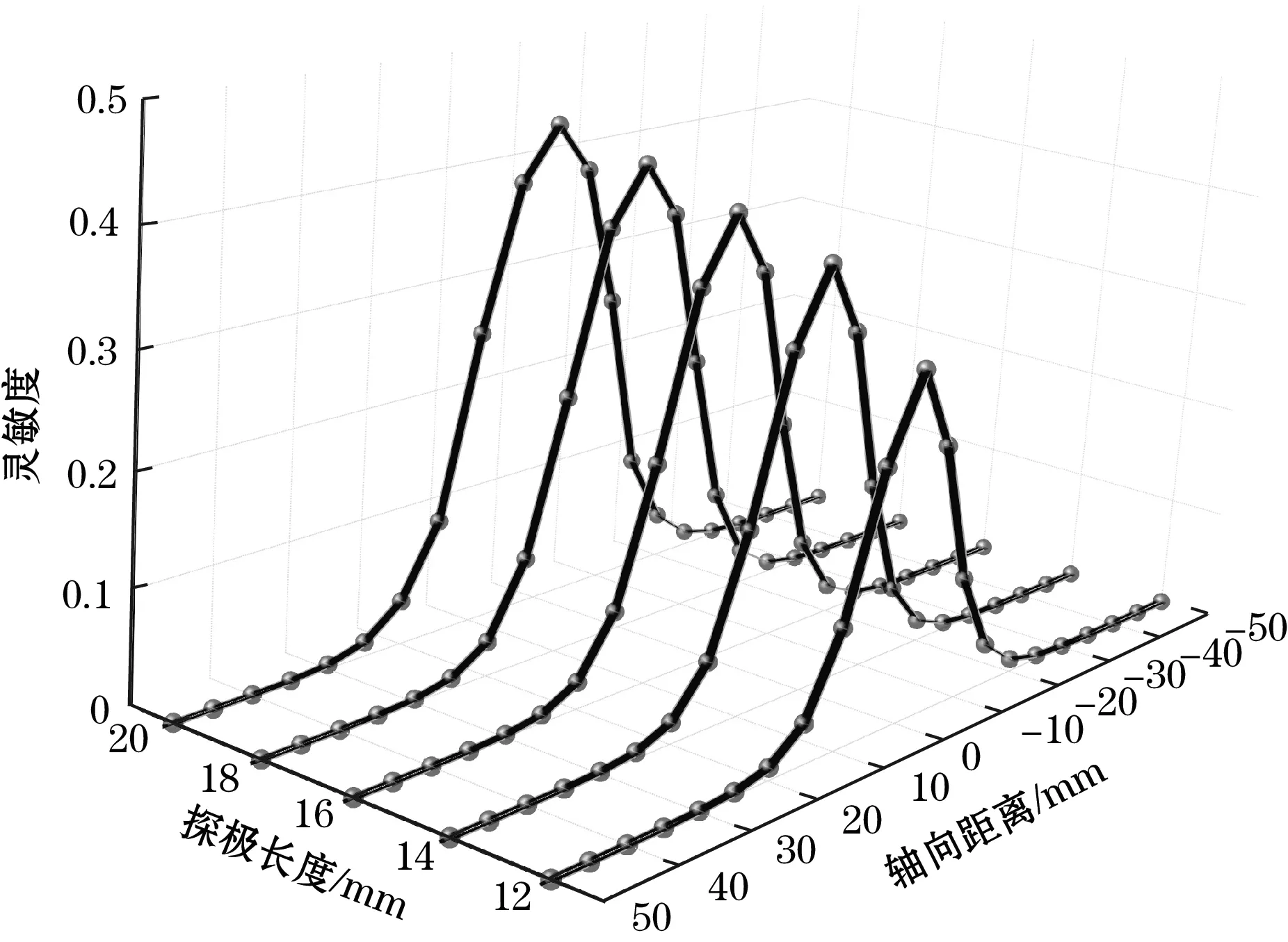
(a)探极直径D=20 mm固定，长度变化

从图7(a)中可看出，当在同一径向位置时，随着探极长度的增大，传感器灵敏度也在增大。说明当探极直径固定时，通过增大传感器的长度可增大传感器的灵敏度。从图7(b)中可看出，图中灵敏度分布分为两部分，点电荷在探极对应长度的外部时，灵敏度随着探极直径的增大而增大，而点电荷在探极对应长度的内部时，灵敏度随着探极直径的增大而不断减小。对于传感器的研究工作更注重探极内部区域的灵敏度情况。因此当探极长度固定时，减小传感器的直径可增大传感器的灵敏度。

3.2 传感器效率特性

传感器效率分为理论效率与工作效率，理论效率可以通过仿真计算得到，而工作效率需要通过实验获取，因此本文将依据仿真得到的结果着重对理论效率进行分析。理论效率公式表示为

η=-QC/q×100%

(4)

式中：η为传感器理论效率；QC为点电荷在C处时探极感应的电量。

根据式(4)可知传感器的理论效率也可以看成为传感器在某一特定位置的空间灵敏度。

由3.1中探极尺寸变化所引起的空间灵敏度分布规律可以发现，当探极的长度与直径之间的比值越大时探极内的空间灵敏度也就越大。因此为了更直观对传感器理论效率进行分析，引入探极长度与直径之间的比值λ来进行研究。传感器探极区域内测点是多样的，可以分布在传感器内任何一处，因此需要固定测点才能研究λ与传感器效率之间的关系。基于以上对传感器空间灵敏度的研究可以看出传感器探极中心O点的灵敏度变化最明显，因此可以将O点作为研究传感器效率的参考点。

固定λ，改变探极长度观察传感器灵敏度在轴向上的分布，当λ=0.5和λ=1时的灵敏度分布如图8所示，从图8可以看出当λ固定时，无论探极长度发生怎样的改变，中心轴线上0点处的灵敏度始终聚在一点，大小保持相等，但当λ值改变时，对应的0点处的灵敏度也随着变化，也即意味着传感器效率在变化。固定λ，改变探极直径也有相同的结论。

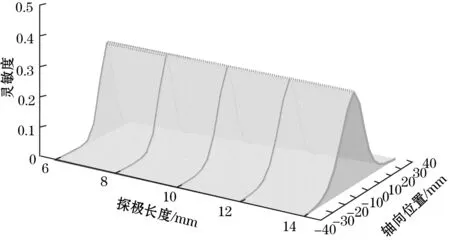
(a)λ=0.5时不同H的点电荷在轴向的灵敏度分布

为了验证规律，取不同λ下仿真出的灵敏度变化趋势(传感器理论效率的变化趋势)如图9所示。从图9可看出，λ越大时，传感器效率也越大，但随着λ的增大，效率先增长较快，当增大到λ=2后，将趋于平缓，理论效率会始终低于0.5。

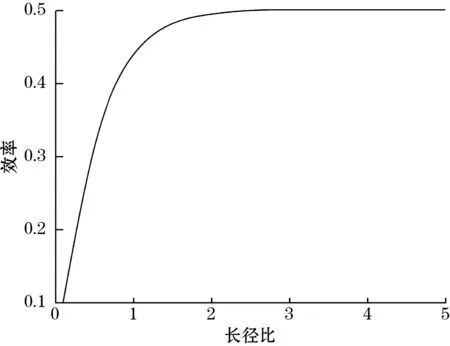
图9 O点处传感器效率随λ的变化趋势

3.3 有限元与数学模型对比

在数学模型中，为了得出环状探极感应的电荷量Q，需要建立以环形探极中心O为原点，探极轴向为z轴，探极中间截面为xOy平面的理论模型，如图10所示。探极的长度为2L,直径为2R，假设点电荷q在探极内的位置为A(x,0,z)，A点在平面内的投影为Ax，x和z分别表示点电荷在探极内的径向和轴向位置。此时，探极上感应电荷量Q为

(5)

式中φ为探极在平面上任一点Aφ与坐标原点的连线和OAx之间的夹角。

图10 OLS数学模型

利用数学模型和公式可以完成对OLS的空间灵敏度与效率的特性计算分析，结果显示当施感电荷越靠近探极感应面，探极中产生的探极感应量也越大即空间灵敏度越大；探极的长径比是影响传感器效率的直接因素，效率随着长径比增大而增大。将有限元仿真结果与理论结果进行对比发现两者关于传感器特性的结果是一致的，验证了所建有限元模型的正确性。同时在使用有限元仿真分析过程中不仅结合了传感器整体的物理结构，而且对于影响传感器监测的外界因素也进行了相应的考虑，从而能够在一定程度上减少一部分需要假设的条件，使对静电传感器的分析研究更简便和准确。

4 结束语

本文根据静电监测原理，基于ANSYS对润滑油路静电传感器进行有限元建模，针对空间灵敏度和传感器效率等特征参数进行仿真分析，结果表明径向位置固定时，点电荷距离探极中心的横截面越近时灵敏度越大；轴向位置固定时，探极内部点电荷越接近探极中心轴线时灵敏度越小，探极外部灵敏度分布规律则相反。传感器探极长度与直径的比值是影响传感器效率的重要结构参数，其效率随探极长度与直径的比值的增大而增大。且该仿真结果与理论模型计算结果变化趋势相一致，进一步验证了有限元仿真方法对静电传感器特性研究的适用性，对后续使用该方法研究结构更复杂的润滑油路静电传感器的性能提供参考。