基于复Morlet小波的列车走行部轴承故障监测系统
2022-09-26李俊曹伍川辉李恒奎
李俊曹,伍川辉,李恒奎
(1.西南交通大学机械工程学院,四川成都 610031;2.中车青岛四方机车车辆股份有限公司,山东青岛 266111)
0 引言
随着轨道交通行业的快速发展,列车的运载要求剧烈增加,走行部作为列车与钢轨接触的重要部分,是保证车辆安全、稳定运行的核心部件。走行部的故障会对列车产生巨大的安全隐患,但常规的检测方式难以在车辆运行时掌握走行部的状态,因此列车的走行部在线监测系统是保障列车安全运行的重要措施。
早期的走行部轴承监测系统采用轴温检测的方式[1-2],其检测原理为轴承在故障后会产生大量的热量,通过温度传感器采集温度,判断是否超过报警阈值,但该方法有较大的局限性。不同的位置,轴承温度报警的标准不同,而且轴承的大部分故障对温度并不敏感,当温度达到报警值时,轴承已经出现比较严重的故障。
硬件共振解调[3-4]是一种常用的轴承故障诊断方法。其检测原理为使用加速度传感器采集轴承的振动信号,再将电压信号经过共振解调模块转化为冲击信号,经过高通滤波后对冲击信号调制,再求出信号的频谱图,根据轴承的故障特征频率判断轴承是否出现故障。该方法对轴承的故障检测较可靠。但该方法的共振频率不能改变,易受外界干扰,采样频率较低,难以发现轴承的高频故障,系统的适用性受到限制。
本文提出的列车走行部轴承故障监测系统,将数据采集、数据处理,数据传输和存储分开设计,并将故障诊断数据通过MVB系统传递给列车主控,提高该系统的实时性,为解决硬件共振模块采样频率低,难以检测高频故障等缺点,该系统采用数字化处理方式,提高系统的采样频率,使用谱峭度[5]找出轴承的共振频率,再用复Morlet小波[6]对数据进行故障诊断,提高轴承故障诊断的精度。
1 系统整体设计
走行部轴承故障监测系统为车载系统,在车辆运行时动态对轴承进行故障诊断,确保轴承故障在早期及时发现,保证列车运行的安全。
该系统由数据采集模块、数据处理模块、数据储存模块和通信模块组成。为满足系统与列车主控的通信和数据的存储,在列车的动车箱安装了通信板和硬盘;为了保证监测系统的稳定性,本系统采用双主机冗余设计,避免一台主机故障后,故障信息不能及时上报、数据丢失等状况。系统的整体框架设计如图1所示。
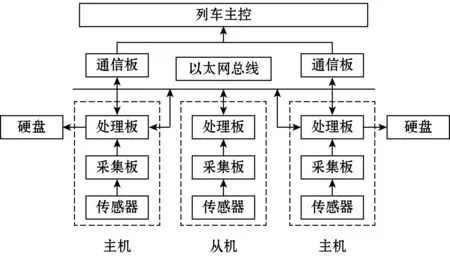
图1 系统设计图
1.1 数据采集模块
数据采集模块主要完成轴承振动和温度数据的采集,并传输给数据处理模块,该模块由复合传感器、A/D转换芯片和数据采集板组成。
复合传感器具有灵敏度高、测量范围广、抗干扰能力强等特点,能可靠测量轴承的振动和温度信号,广泛运用于铁路等领域,将其安装在走行部的轴箱、齿轮箱、电机等位置,实物安装图如图2所示。

(a)传感器安装图
A/D转换芯片采用AD7606,是一款8通道同步采集模数转换器,每通道最快采样速度为200 KSPS,每通道的位数为16。能够满足系统的采样频率的要求。将复合传感器输出的电压信号转换为数字信号。
数据采集板采用ARM Cortex-M4内核的STM32F407微处理器,通过FSMC总线通信协议,采集AD7606转换的振动信号,FSMC为16位的并行采样电路,能极大地提高数据采集的频率,采集板采用分时复用的方法采集各个轴箱、齿轮箱、电机箱的振动信号,并通过SPI总线将采集的数据传输给数据处理模块。
1.2 数据处理模块
数据处理板采用ARM3354芯片,该芯片支持运行linux系统,能够支持多线程运行,支持系统完成多任务操作。处理板需要接收采集板的数据,对数据进行轴承故障诊断算法处理,将诊断结果与原始数据上传给主机,主机将各车厢的原始数据和诊断结果保存到硬盘,并将诊断结果上传给列车主控,处理板的安装图如图3所示。

图3 处理板安装图
处理板对轴承的诊断流程如图4所示,该方法利用快速谱峭度法求出轴承的共振频率和带宽,以此确定复Morlet小波的小波系数,可以根据信号自适应地确定小波系数,提高了故障诊断的自适应性与精确性。

图4 故障诊断流程图
诊断的具体步骤如下:
(1)使用快速谱峭度法对传感器采集的振动信号x(t)进行分析;
(2)根据最大谱峭度原则确定共振频率和带宽;
(3)根据共振频率和带宽,确定复Morlet小波的中心频率和尺度;
(4)根据小波系数对信号进行小波变换;
(5)构造解析信号;
(6)对解析信号进行包络解调;
(7)对包络信号进行FFT变换,求出频谱图;
(8)根据轴承内环、外环、滚动体的故障频率与频谱图峰值较大的频率进行比较,以此确定轴承的故障状态。
系统运行的整体流程如图5所示。
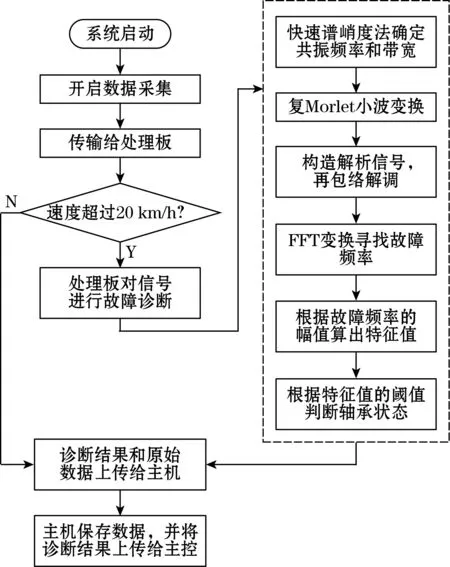
图5 系统流程图
2 轴承故障诊断原理
共振解调法在工程中广泛应用,其基本原理为故障轴承工作时会产生宽频带的冲击信号与传感器产生共振,根据共振频率对采集的数据进行带通滤波,然后进行包络解调,分析轴承的故障。但共振解调法难以确定信号的共振频率,所以该方法不能有效地消除噪声的干扰,诊断精度不高。
本文提出了一种基于谱峭度和复Morlet小波的轴承故障诊断方法,利用谱峭度对瞬态信号敏感、抗干扰能力强的特点,自适应地提取信号中的共振频率和带宽,以此可以确定复Morlet小波的系数,利用复Morlet小波兼具带通滤波与信号包络的特性对信号进行处理,提高故障诊断的精度。
2.1 谱峭度
谱峭度是基于峭度发展的一种高阶统计量,其本质是计算出每根谱线的峭度值,从中找出信号中的非平稳成分,并计算出所在的频带。
轴承的振动信号为非平稳信号,对于非平稳信号可以采用Wold-Cramer分解[7-8],将输入信号x(t)分解为Y(t):

(1)

(2)
式中:Y(t)为系统响应;H(t,f)为系统的时变传递函数,即Y(t)在频率f处的复包络;X(f)为与x(t)相关的谱过程;j为虚数单位。
实际的系统中H(t,f)并不确定,可使用H(t,f;w)表示,w表示滤波器时变性的随机变量。
非平稳信号的特征信息可以通过统计指标来获取,在此引入瞬时矩。瞬时矩是关于时间和频率的函数,广泛用于非平稳过程的分析,由此求出信号的2n阶瞬时矩为
S2nY(t,f)=E{|H(t,f)dX(f)|2n|w}df
=|H(t,f)|2nS2nX
(3)
式中S2nY(t,f)为Y(t)的2n阶瞬时矩。
对周期内的瞬时矩取平均可以得到:
(4)
式中:〈S2nY(t,f)〉t为时均矩;T为时间周期。
非高斯性是非平稳过程的最大特点,谱积累量常来表示信号的非高斯性。在非高斯过程中,阶数大于等于4的谱积累量不为0,则4阶谱积累量为
(5)
信号的非高斯性程度越大,其4阶谱积累量越大。所以信号概率密度在频率f处的峰值可以用4阶谱峭度来测量,其定义如下;
(6)
对轴承的振动信号建立简化的数学模型如下:
W(t)=X(t)+S(t)
(7)
式中:W(t)为加速度传感器采集信号;X(t)为共振信号;S(t)为其他噪声信号。
S(t)与X(t)为独立的信号,则可以算出W(t)的谱峭度为
(8)
式中:S2S(f)为噪声信号S(t)的时均矩;S2X(f)为共振信号X(t)的时均矩;ρ(f)为噪信比。
谱峭度KW(f)是关于频率f的函数,从式(8)可以看出,当ρ(f)较小时,近似等于KX(f);当ρ(f)较大时,KW(f)近似为0。使用快速谱峭度法能对轴承的振动信号进行全频段的分析,可以确定出轴承的共振频率和带宽。
2.2 复Morlet小波
小波变换解决了短时傅里叶变换窗口大小不能随频率变化而改变的缺点,将傅里叶变换的三角函数基变为有限长会衰减的基,通过对小波基的伸缩平移来对信号进行时频分析。
根据实际应用需求可以选择不同的小波基,本文为了分析轴承的故障采用复Morlet小波,其波形与冲击信号类似,因此广泛应用于冲击信号检测。复Morlet小波[9]的定义为
(9)
式中:t为时间;f0为中心频率;σ为控制小波窗口宽度;i为虚数单位。
将f0设置为1 Hz,σ设置为1.5,画出复Morlet小波实部在时域的波形,如图6所示。

图6 复Morlet小波实部时域图
Morlet小波时域到频域的转换公式为
(10)
根据式(10)将复Morlet小波从时域转换为频域,画出不同σ对应的小波的频域,如图7所示。可以看出复Morlet小波在频域内具有高斯窗口函数的形状,不同的σ可以控制小波在相同频率下的带宽,因此复Morlet小波可以作为中心频率和带宽可调的带通滤波器。

图7 复Morlet小波频域图
根据式(9)可以将复Morlet小波分为实部和虚部,表达式为:
(11)
(12)
式中:Ψr(t)为实部;Ψi(t)为虚部。
根据式(11)和式(12)可以发现,信号经过复Morlet小波变换后,其实部和虚部的相位相差90°,与Hilbert变换的效果一致,将振动信号x(t)进行小波变换得到解析信号S(t),对S(t)进行包络为
(13)
式中:X(t)为包络后的信号;Re为解析信号的实部;Im为解析信号的虚部。
3 轴承诊断效果验证
将故障数据导入数据采集板,模拟采集板采集的轴承振动信号,再传给数据处理板进行轴承故障诊断,以此来验证振动算法的有效性。
本文使用的验证数据来自美国凯斯西储大学轴承数据中心,实验设备由1.5 kW的电动机、扭力传感器、功率测试仪和电子控制器组成。
该实验平台分别对驱动端轴承和风扇端轴承的振动信号进行采集,驱动端轴承采用6205-2RS JEM SKF 深沟球轴承,风扇端轴承采用6203-2RS JEM SKF 深沟球轴承,其参数表如表1所示。

表1 轴承参数表 mm
该实验室分别采用12 kHz和48 kHz的采样频率对正常轴承、内环故障轴承、滚动体故障轴承、3点钟外环故障轴承、6点钟外环故障轴承、12点钟外环故障轴承在不同转速和不同损伤直径下采集轴承的振动数据。
本文采用驱动端轴承的数据进行分析,使用转速为1 797 r/min,采样率为12 kHz,内环故障直径为0.177 8 mm的振动数据,根据相应参数计算出该轴承的故障特征频率[10],如表2所示。

表2 轴承故障特征频率 Hz
取内环故障轴承振动数据中的1 s进行分析,其原始数据如图8所示。

(a)内环故障轴承原始数据时域图
从图8(b)可以看出,轴承的故障信号被淹没在大量的噪声中,直接使用傅里叶变换不能有效地提取出轴承的故障信息。
使用快速谱峭度法[11-12]对振动数据进行分析,得到谱峭度图如图9所示。根据图9可以看出,谱峭度最大值对应的中心频率为1.750 kHz,带宽为500 Hz,根据谱峭度最大值原则确定共振频率为1.500~2.000 kHz,根据快速谱峭度法求得的共振频率和带宽f,可以求出复Morlet小波的尺度为
scal=fs·wcf/f
(14)
式中:scal为复Morlet小波的尺度;fs为采样频率;wcf为复Morlet小波的中心频率;f为带宽。
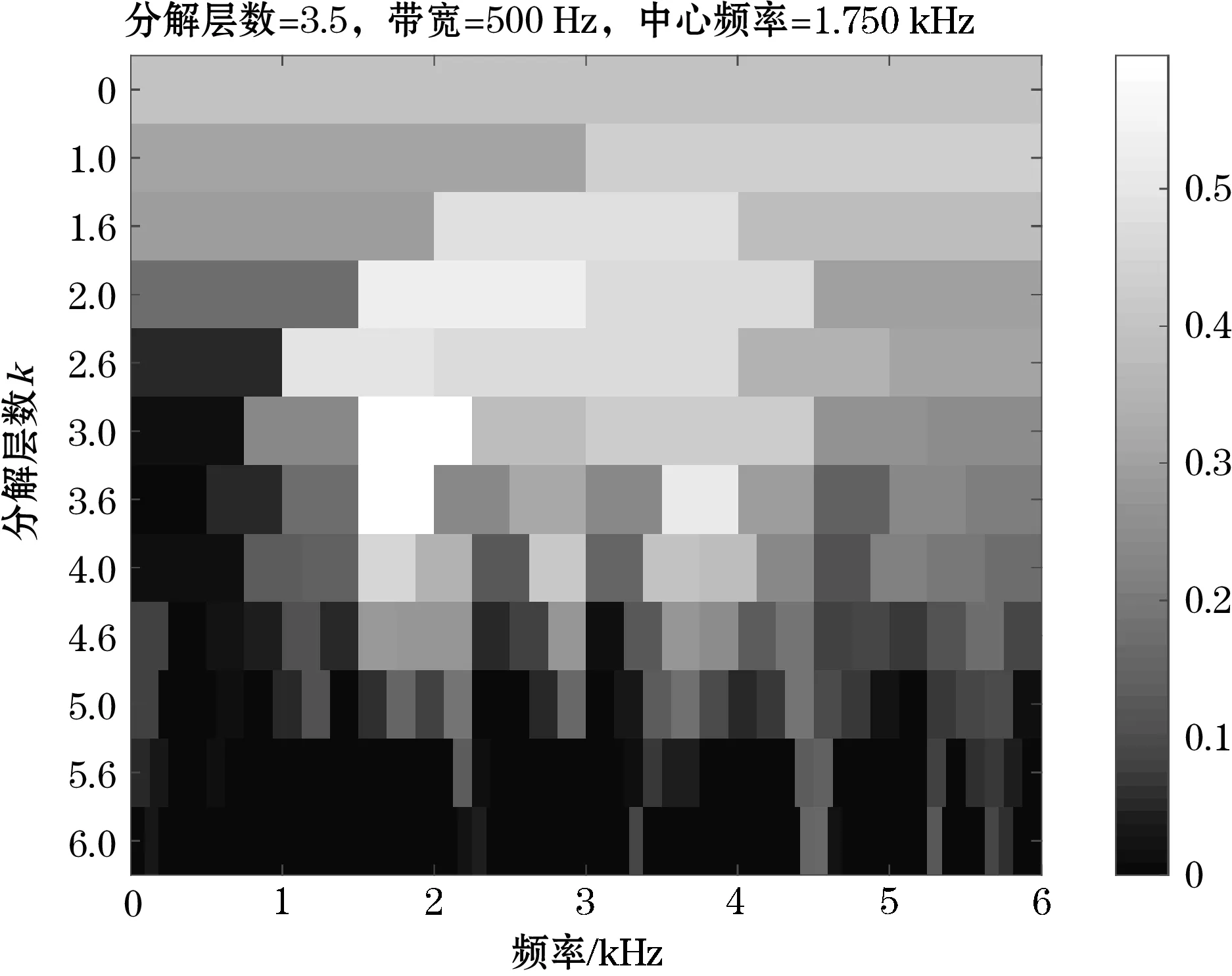
图9 内环故障轴承振动数据谱峭度图
根据复Morlet小波的中心频率和尺度可以求出其小波系数,对原始信号进行小波变化后,得到解析信号如图10所示。再对该解析信号进行包络解调,如图11所示。

图10 内环故障轴承小波变换后的解析信号
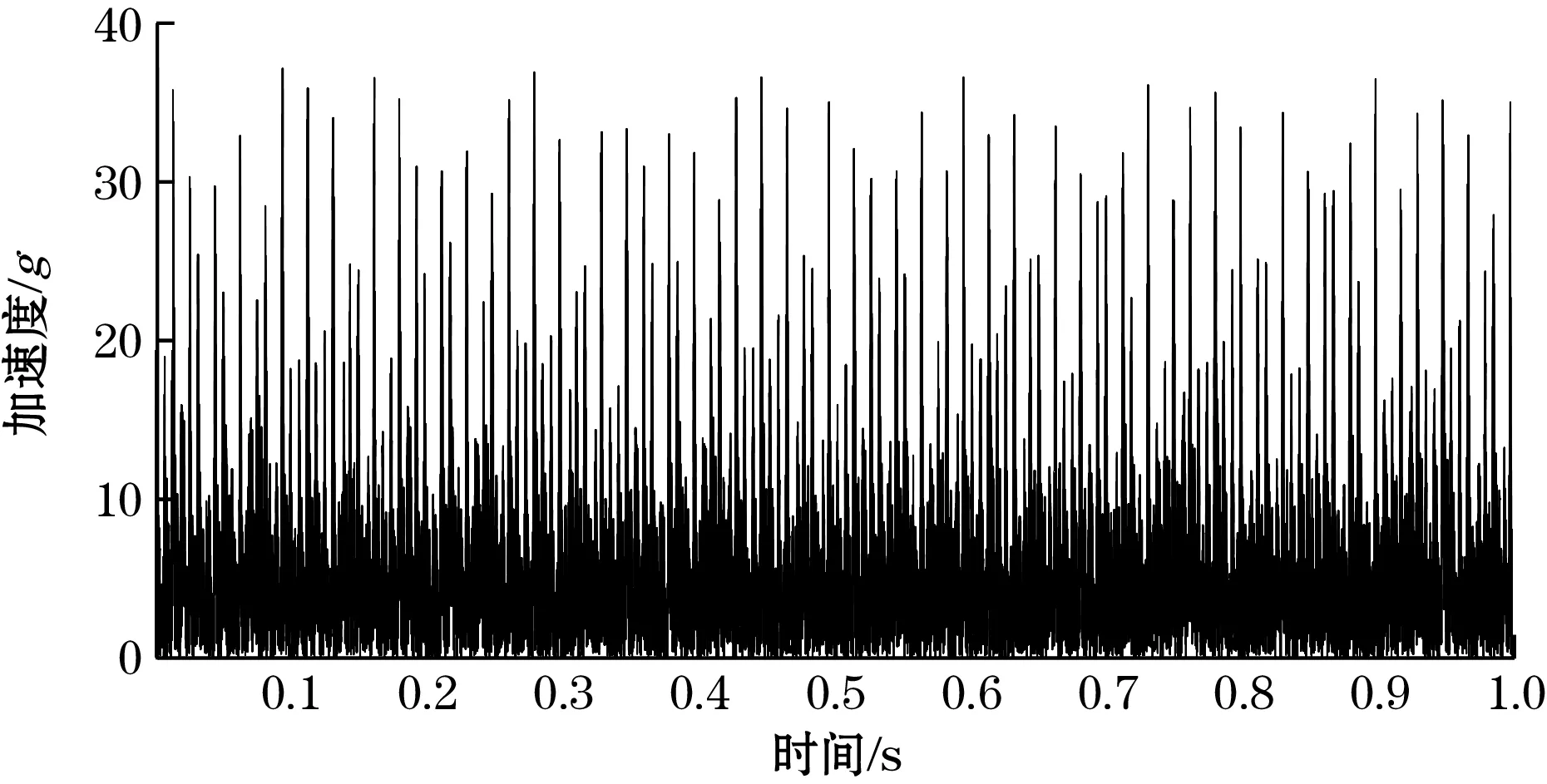
图11 内环故障解析信号包络时域图
对包络信号进行FFT变换找出轴承的故障频率,如图12所示。根据表2可以找出此轴承内环故障频率为162.2 Hz,从图12可以看出,在163 Hz处出现峰值,与轴承内环故障频率接近,该算法精准地找出了内环轴承的故障。

图12 内环故障解析信号包络频域图
找到故障频率对应的幅值,将其转换为dB值,转换公式为
dB=20·lg(x/y)+B
(15)
式中:dB为信号强度;x为故障频率对应的幅值;y为轴承正常时的幅值;B为信号强度的补偿值。
判断轴承内环故障频率求出的dB值是否超过报警阈值,来确定报警等级。
4 结束语
本文提出的走行部轴承故障监测系统,将数据采集与数据处理分离,通过快速谱峭度法确定信号中的共振频率,并且可以根据振动信号自适应地调节复Morlet
小波的中心频率和尺度,以此更好地抑制外界噪声的干扰,提高轴承故障诊断的准确性。基于模拟轴承故障实验,该系统能精确地检测出轴承的故障特征,并上报给列车主控,能够满足轴承故障检测的需要,为走行部轴承故障检测提供了有效的检测方法。
