基于DSP与FPGA的电容绝对式编码器的设计

邵小彪，丁红昌,2，曹国华,2

(1.长春理工大学机电工程学院，吉林长春 130022；2.长春理工大学重庆研究院，重庆 401135)

0 引言

编码器精度高、灵敏度高、结构简单、功耗低，被广泛应用于各个领域，能够及时有效地测量和反馈角度和位移信息[1-3]。目前，绝对式编码器具有精度高、寿命长、测量方便、能反映绝对位置信息等优点。然而，传统传感器细分电路复杂，响应速度慢。对于增量式编码器，只能确定旋转角度，不能及时有效地反馈绝对位置信息。单圈绝对式编码器只能确定一圈内的绝对位置信息，当角度大于360°时，部分信息会丢失。绝对式编码器虽然可以有效反馈大于360°的角度信息，但需要多套码盘，设计较复杂。

因此，本文仅使用2组码道，利用DSP的高速信号采集和计算能力以及FPGA的灵活性和并行处理能力，计算出这2组码道的波形，确定其绝对位置信息[4-5]，最后通过RS485通信接口将得到的数字角位置传输给计算机。大量的实验数据表明，文中编码器能耗低、结构简单、测量精度高以及测量稳定，可以实现对角度在线测量[6]。

1 基本原理与设计

1.1 传感元件

电容式编码器的基本传感元件由定子和转子组成，均采用标准PCB技术制成。定子通过螺孔固定在金属外壳上，转子与随元件旋转的轴连接。定子面对转子的一侧覆盖着发射电极和接收电极。转子分为两部分，外圈对应精机，采用64对极的锯齿波形，内圈对应粗机，采用3对凹形图形。为了减小电容角位移传感器的结构尺寸，信号处理电路安装在接收极定子的另一侧。精机发射电极和粗机发射电极做成栅状分布，各个栅极间存在屏蔽电极，防止相邻电极间的电容耦合。激励信号通过半孔和过孔引线连接到发射电极群。在接收电极和反射电极周围，使用圆形保护电极以减少外部干扰的影响。编码器整体示意图如图1所示。

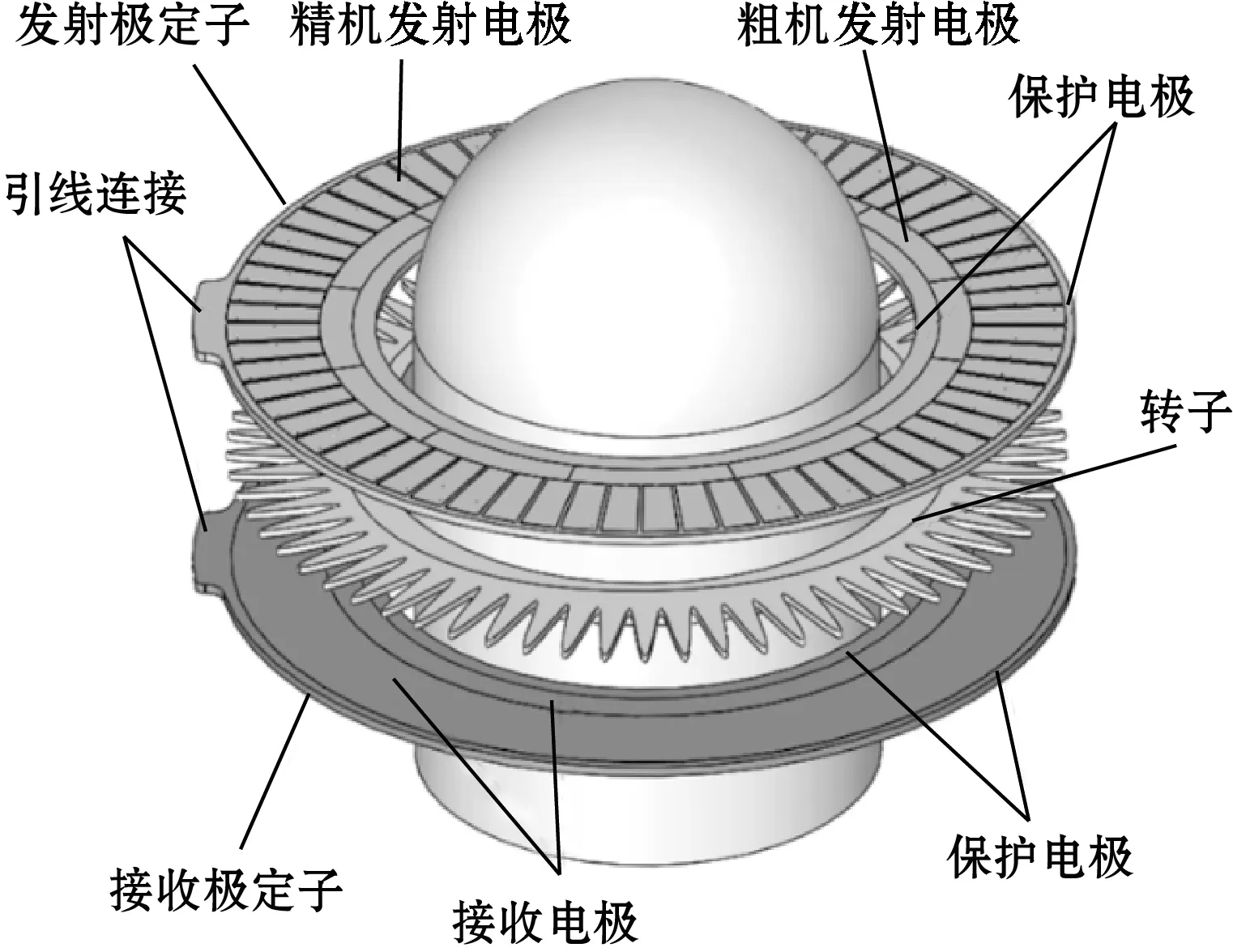
图1 电容式编码器的结构模型

1.2 测量原理

电容式旋转编码器的原理图和电路模型如图2和图3所示。图中曲线表示转子的轮廓，分为外圈的正弦形状和内圈的凹形形状，转子旋转时可以产生相关的幅度调制正余弦信号；扇区表示定子的发射极，分成N组栅极的外圈精机和M组栅极的内圈粗机。转子的内外圈波形在极坐标下的方程表示为：

(1)

式中：R为精机中心圆半径；Am为精机幅值；φ为机械转角；N为精机栅极组数，设计为64组；r为粗机中心圆半径；Bm为粗机幅值；M为粗机栅极组数，设计为3组。

图2 电容式编码器的示意图

图3 电路模型图

(2)

式中：λ为每个发射段的角宽度，每一发射段处于正弦波的4个相位之一，且0<λ<(2π/N)；θ为转子旋转角度，θ=N·φ，表示电旋转角度是机械角的N倍。

同理，可计算粗机发射电极与粗机接收电极之间形成的可变电容，表示为：

(3)

式中：γ为每个发射段的角宽度，每一发射段处于正弦波的4个相位之一，且0<γ<(2π/M)。

图2中的精机发射极的电极组A、B、C、D和粗机发射极E、F、G、H连接到由FPGA产生的4路相位相差π/2的方波V1、V2、V3和V4，其频率为25 kHz。用函数表示为：

(4)

式中n=1,2,3,4,5，…。

一组电极上的电荷是电容乘以4个激励电压，则整个精机传感器的电压为

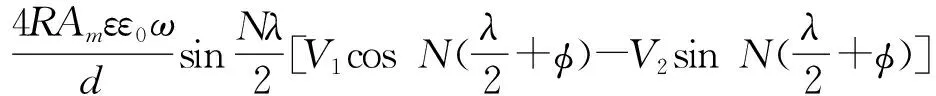
(5)

同理，第二发射极和接收极的工作情况与上述相同，粗机整个传感器得到的电压输出为

(6)

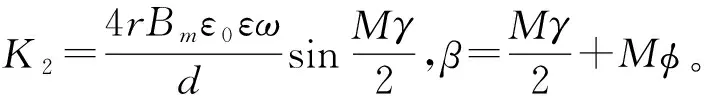
电容式编码器输出精、粗两路调制电压为U(t)和V(t)。但精机sinα、cosα信号或粗机sinβ、cosβ信号，相对于高频方波激励信号，变换非常缓慢，方波激励信号可认为是其载波信号，因此，需要通过幅频检波电路把正余弦信号进行提取，检波的原理图如图4所示。

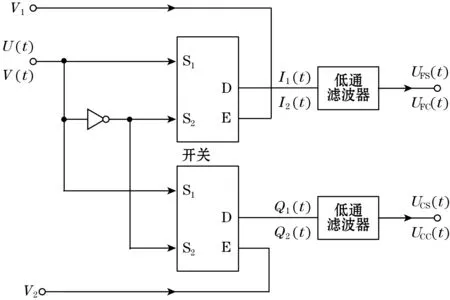
图4 检波原理图

本文设计的编码器选用同步检波方法，由于采用方波激励信号，不能采用乘法方式进行检波，因此采用开关电路对调制信号进行检波。方波激励信号V1、V2作为开关选择信号，对调制信号进行频谱迁移，使调制信号的相角α、β信息迁移到低频区，激励频率迁移到高频区，得到信号I1、I2、Q1和Q2，然后经过低通滤波器过滤掉高频信号，可得到相位角正余弦信号UFS、UFC、UCS和UCC。信号I1、I2、Q1和Q2表示如下：

(7)

相位角正余弦信号UFS、UFC、UCS和UCC表示如下：

(8)

通过反正切可求得α和β，最后再通过正切细分法，经过DSP和FPGA软件计算可得到精确的角度信息。

2 硬件电路设计

2.1 总体方案设计

样机的信号处理架构如图5所示，包括激励模块、转换电路模块与角度解算模块部分。

图5 电容绝对式编码器的信号处理结构

信号激励模块由FPGA和放大电路组成。通过FPGA产生4路90°相位差的25 kHz方波激励信号，该信号经过放大处理后作为编码器的激励源。

转换电路模块包括信号放大电路、信号检波电路以及增量转换电路。高频激励信号施加在发射电极后，动板的转动影响敏感区电容的耦合，产生的精机和粗机两路微弱的信号，经过信号放大电路然后进行检波和滤波处理，最后再进行增量转换形成可供AD采集的信号。

角度解算模块包括AD采集角度解算以及RS485通讯。经过转换电路后的信号送至DSP中的AD转换器进行采集，然后进行角度解算，最后通过RS485发送至上位机，在上位机中可以实时显示角度位置的变化，以供后续误差分析使用。

2.2 激励信号

激励信号电路的设计如图6所示。由FPGA控制器A1、A2、B1、D1引脚产生4路相差T/4周期的方波信号作为电容角位移传感器的激励信号。4路激励信号施加到芯片HEF4104BT的4、5、11、12引脚上，HEF4104BT芯片将4路激励信号保持和取反输出并且激励信号由芯片1引脚的电势作为参考电压，使激励信号幅值放大4倍，得到8路高压激励信号，4路用于精机，4路用于粗机，直接施加到精机和粗机的发射电极上。

图6 高频激励信号电路

2.3 信号转换电路

2.3.1 信号放大电路

高频激励信号施加在发射电极后，动板的转动影响敏感区电容的耦合，产生精机和粗机两路微弱的信号。因此，信号需要经过放大，便于后续滤波和检波。本文设计放大电路采用电流和电压两级放大，主要采用AD8512ARM芯片进行电路的放大设计，其电路设计如图7所示。

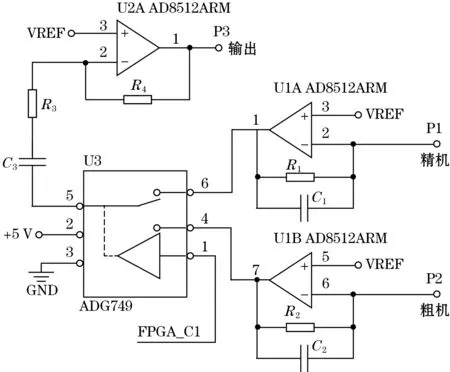
图7 放大电路

信号输入到AD8512ARM芯片的2引脚和6引脚中，在3引脚和5引脚上施加参考电压，电流放大器采用交流锁相电容放大器，负反馈调节。放大的电流信号输入ADG749芯片的6引脚和4引脚，FPGA的C1引脚控制ADG749芯片对粗机、精机通道进行选择，5引脚输出电流信号过滤掉交频信号，进入电压放大器。经过两级放大和滤波后，信号具有较好的质量。

2.3.2 检波电路

经放大电路处理过的信号中含高频激励信号和噪声信号，因此需要一种有效的检波电路对信号进行频谱分离和滤波，使含有动板机械角度的基波与高频信号分离。电容角位移传感器采用同步检波，设计开关选通电路对信号波处理，电路如图8所示。

图8 检波电路

检波电路采用ADG749芯片的开关电路对调制信号进行同步检波。反向电路由电阻R1、R2和运算放大器U1B构成，对信号取反，U1B放大器的输出信号与输入信号同频同幅，相差T/2个周期。U2、U3芯片对两路信号进行检波调制，FPGA输出同频的方波信号V1、V2作为开关的选择信号，对两路相位差180°的调制信号U(t)和V(t)交替选通，进行频谱迁移，含动板机械角度的正余弦调制信号迁移到低频区，激励频率迁移到高频区，高频调制信号与基波信号的分离，有利于细分电路对基波相位角的提取。

2.3.3 增量转换电路

增量转换电路用于动板旋转方向的判别，设计如图9所示。通过电压比较器LMV726把正余弦信号转换成正交增量A、B脉冲信号。正余弦信号转换成TTL脉冲信号，以便实现对传感器整周期信号进行四倍频计数。由可DSP正交编码模块对脉冲信号上升沿/下降沿采集，判别电容角位移传感器动板的转向等问题。

图9 增量转换电路

3 软件系统设计

3.1 软件流程

电容角位移传感器信号处理系统的结构体由电路硬件设计完成，具体功能依靠软件设计实现。为实现编码器的高效计算速度，采用以可编程逻辑器件FPGA和数字信号处理芯片DSP双处理器为核心的软件计算，提高传感器的响应速度。软件设计主要包括DSP和FPGA同步时钟、激励信号的产生、AD采集模块、角度计算与转换模块(含细分)、与上位机通信等，软件流程如图10所示。

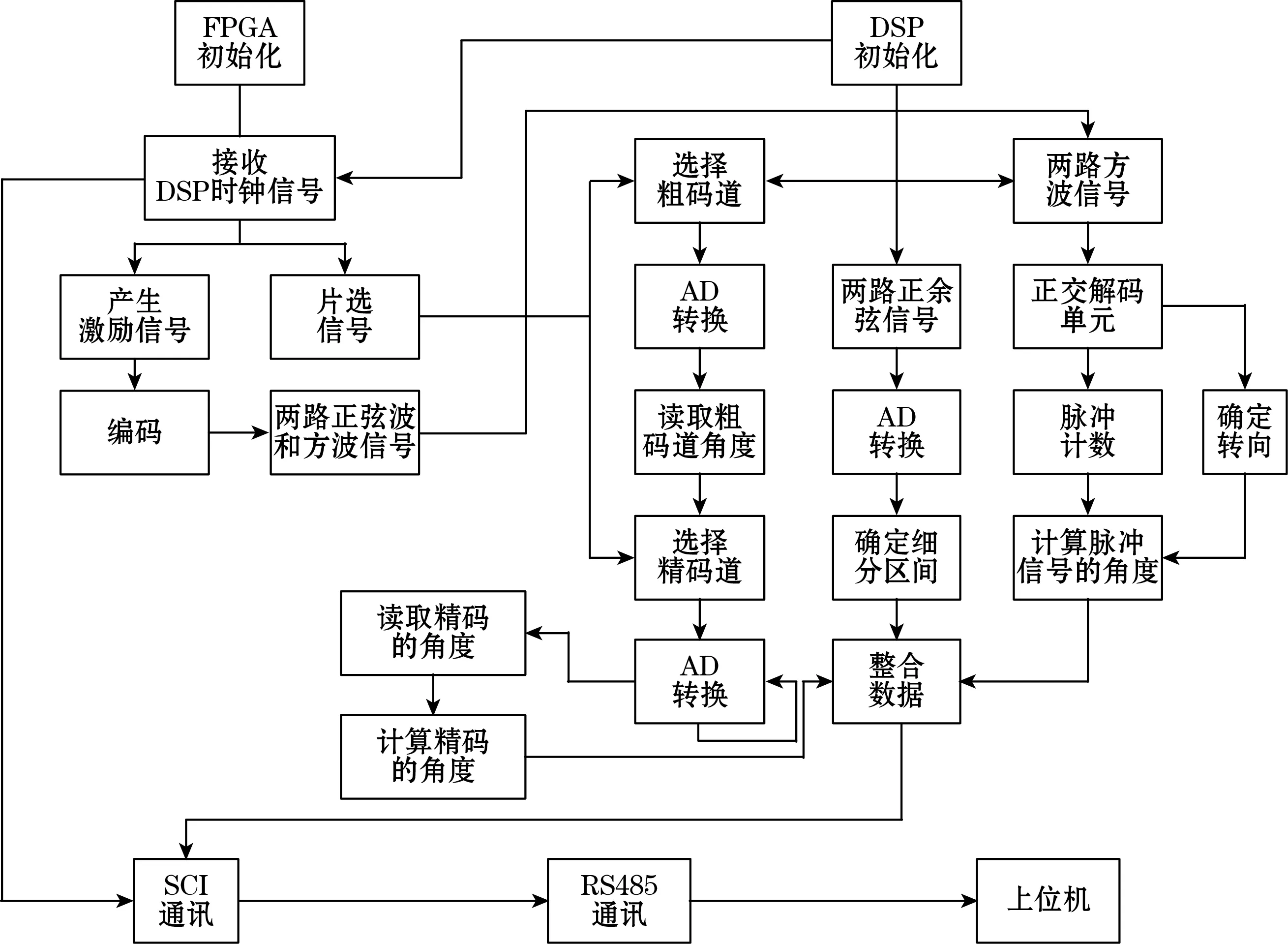
图10 软件流程图

编码器上电后，FPGA接收DSP发送的时钟信号，产生4路方波激励信号和开关选通信号，控制放大电路分别采集2组码道信号。信号经过硬件电路处理后，得到两路方波信号和两路正余弦信号。使用DSP中的ADC采集正余弦信号后，即可得到初始位置。方波信号则由正交解码模块解算，以确定旋转的粗略角度。ADC获取正弦和余弦信号再进行细分得到精确的角度。ADC采集和QEP设置中断，角度发生变化时，数据将会实时采集和更新，将采集到的数据取出，为计算角度做准备。角度计算完成后由DSP发送给FPGA，再由FPGA通过RS485接口将获得的角度值发送至上位机。

3.2 细分和绝对位置计算

使用细分将正弦和余弦信号划分为区域以提高精度[8-9]。根据正余弦信号的幅值、交点、峰值的关系，将1个周期分为8个区间，每个区间为45°，对45°区间进行处理，得到一个无符号的正余弦函数波形。象限Ⅱ和象限Ⅳ的正弦和余弦函数波形完全相同，周期可以从2π减小到π/2，如图11所示。

图11 正弦和余弦信号的细分

通过比较2组码道的角度，将编码器的实际位置颠倒过来。由于2组码道所表达的角度信息是相同的，因此可以使用以下公式计算：

360/12·M+a=360/64·N+b

(9)

式中：a、b为DSP解析的准确角度信息；M的取值范围为0～63；N的取值范围为0～3，为整数。

如果给出参考误差，则可以确定初始绝对位置信息，如图12所示。

图12 绝对位置计算

4 实验结果与分析

4.1 实验结果

该软件是根据实验原理设计的。对2个方波的脉冲数进行分析得出的总脉冲数，总脉冲数减1，乘以360/64就是粗略的旋转角度。精确的角度值由ADC收集。脉冲通过QEP1A和QEP1B连接。收集的脉冲数在QPOSCNT寄存器中。设置时钟频率为100 MHz，采用QEP计数模式，自由运行模式，标记第1个索引事件的发生，并在索引信号的上升沿锁存。如果发生索引事件，计数器的值将被重置。在这种模式下，读取的值需要除以4才能得到脉冲总数。将测量的角度通过加减360°，确保它在0°和360°之间。

如图13所示，q为采集的脉冲数，c11和c22为采集的正余弦信号。在计算出正交解码单元和反正切函数后，可以有效地计算出编码器旋转过的角度，加上起始位置的角度，可以确定最终的绝对位置信息Z并转换为0°到360°的范围，用变量W表示。

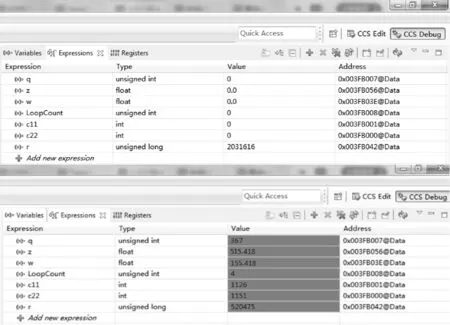
图13 DSP数据解决方案图

4.2 样机和实验平台

图14和图15为测试原型的实验装置示意图和实物图。该装置由高精度光电编码器、实验台、信号采集电路和步进电机等组成，转台分辨率0.62″。步进电机用来改变角位置和角速度，传感器安装系统的设计目的是将转台与转子连接起来，调整转子与定子之间的同心度和平行度。转子直接安装在转台的轴上，定子固定在安装系统的支架上。使用高精度光电编码器测量转子的角位置作为参考。当转子停在某个位置时，可以测试编码器的精度，当转子以某个速度旋转时，可以测试整个范围内的速度和动态非线性，角位置通过数据采集模块发送给上位机。

图14 试验台结构示意图

图15 检测试验台

4.3 测量结果

当步进电动机静止时，数据采集电路采集电容传感器转子角位置，用Matlab软件将采集的数据绘制出来，其角位置波动程度如图16所示。从图中可以得出结论，电容角位移传感器测量误差在0.006°上下波动，传感器测量精度优于0.007°。

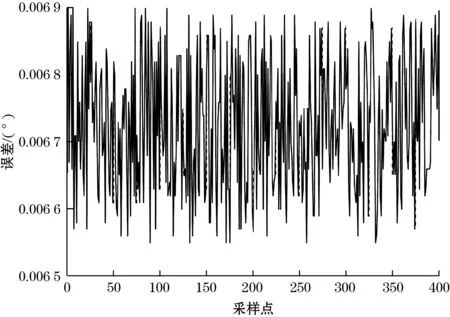
图16 转子静止时测量角度波动

当步进电机以一定速度匀速旋转时，数据采集电路采集到的角位置数据通过串口通讯，发送给计算机，Matlab绘制角度变化如图17所示，从图可得出动板旋转一个周期需要0.006 s，这和示波器测量出的正余弦信号和增量方波信号的周期吻合，相位关系保持一致。

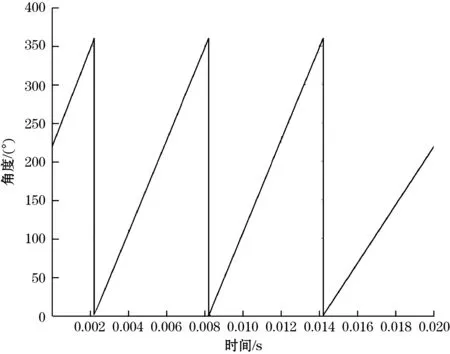
图17 转子旋转时测量角度变化

表1列出了随着步进电机的旋转，作为位置反馈的光电编码器和待检测的电容编码器一个周期内动板机械角度变化的实验数据。表1中列出20组实验数据，最大误差为8.70″，最小误差为0″，计算20组数据的平均误差为4.749″。从实验数据中可得出，本文设计的电容角位移传感器测量精度较高，满足大多数伺服控制系统和测量系统的精度要求。

表1 实验数据和参考基准数值比对

5 结论

文中设计了一种电容绝对式编码器，可以有效计算绝对位置信息，利用DSP的信号处理能力，配合FPGA的灵活性提高效率。编码器转子为正弦图形，转子将角度位置转换为基于正交调制的相位/频率调制信号。然后在基于正交解码和细分原理的DSP和FPGA处理器中，将相位/频率调制信号数字解码为角度位置。这种数字解调系统可以避免信号不平衡问题。在没有外壳屏蔽的情况下，电容式编码器的精度优于9.0″。为了进一步评估和改进电容绝对式编码器的性能，正在搭建更好的实验环境。提高电容式编码器的信噪比、分析边缘场效应以及误差补偿是今后的发展方向。