电阻式传感器智能感知节点误差校准方法研究
2022-09-26郑一鸣陈非凡
陈 猛,郑一鸣,陈非凡
(1.清华大学精密测试技术及仪器国家重点实验室,北京 100084;2.国网浙江省电力有限公司电力科学研究院,浙江杭州 310014)
0 引言
智能感知是智能物联的基础,各类传感器及其智能感知节点是智能物联系统的关键组成部分[1-3]。电阻式传感器被广泛应用于温度、应变、压力、重量、磁场和气体等领域的测量[4-7],在各类智能物联系统的感知网络构建中具有重要地位。
面对众多电阻式传感器的感知需求,若智能感知节点能自动适应不同传感器的阻值测量范围,则可显著减少感知所需的节点种类,从而降低智能物联系统的设计与构建成本。这就需要智能感知节点中的电阻测量电路具有较大的阻值测量范围。
在电阻式传感器测量方法中,比例式电阻测量电路由于不依赖激励电流精度且具备噪声抵偿特性[8],因此常被用于测量铂电阻等高精度电阻式传感器[9-11]。但比例式电阻测量电路的测量范围被限制在参考电阻自身的阻值范围内,扩大电路量程就意味着需要采用更大的参考电阻并降低激励电流,这必然导致小电阻的测量误差较大。为了解决这一问题,本文提出了一种增益自动调节型大范围高精度比例式电阻测量电路的测量误差校准方法,所有校正系数的测定和存储均可由感知节点自身自动完成,大幅降低了节点校准的难度和人工干预程度。在节点10 Ω~22 kΩ的测量范围内选取5个标准电阻进行测量评估,结果表明:该误差校准方法可将节点的电阻测量误差降低90%~99%,校准后节点的测量误差低于±0.01%,可满足铂电阻和热敏电阻等电阻式传感器的阻值宽范围和高精度的自适应测量需求。
1 电阻式传感器智能感知节点
图1给出了电阻式传感器智能感知节点原理框图。节点带有2组完全一致的四端子传感器接口,每个接口均可直接接入1路二/三/四线制的电阻式传感器;MCU负责控制节点的信号调理电路以实现传感器阻值的自适应测量,并将阻值自动转换成传感器的感知信息(如温度等);节点中的测控网络器件可为节点提供自组网测量能力,基于近年提出的信息管道技术[1,12],可与其他功能相同或不同的节点构成分布式智能测控物联网络。
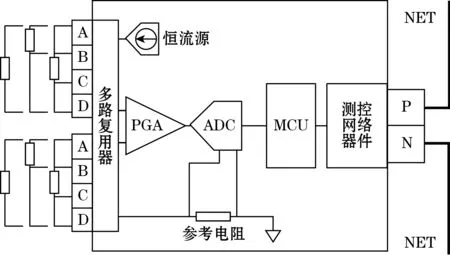
图1 节点原理框图
图2给出了电阻式传感器智能感知节点所采用的增益自动调节型多线制比例式电阻测量电路的工作原理。图2所示的测量电路在传统的比例式电阻测量电路基础上,通过扩大参考电阻阻值并引入可自动配置的多路复用器(multiplexer,MUX)、可编程增益放大器(programmable gain amplifier,PGA)等功能部件,实现了不同线制电阻式传感器的阻值自适应测量,通过动态调节PGA增益,可提升小电阻的测量分辨力。

图2 增益自动调节型多线制比例式电阻测量电路
由于PGA的放大效应,图2所示测量电路的测量误差在不同增益条件下的传递存在明显区别,需要通过某种测量误差校准方法才能实现全量程范围内的高精度测量。
2 测量误差校准方法
图3给出了图2所示智能感知节点电路的测量链路及其误差源分析示意图。其中,Rx为被测传感器的阻值;Dx为被测电阻为Rx时ADC模数转换输出的数字量;N为ADC的转换位数;Is、Rref、A分别为激励电流、参考电阻、PGA所设定增益倍数的标称值;δIs、δRref、δA分别为激励电流、参考电阻、PGA增益倍数相较于各自标称值的相对误差;V1和V2分别为PGA前、后链路中各器件的等效误差电压,主要由偏置电压和噪声电压构成,V1会被PGA放大,而V2则不会;δINL为ADC转换误差,表征ADC实际转换曲线与理论特性曲线之间的偏离程度。

图3 测量链路及其误差源分析示意图
如图3所示,在不考虑各误差源影响时,测量电路的理论测量转换方程为
(1)
可见Dx与Rx成正比,式(1)可改写为
Dx=k0·Rx
(2)
k0为理论测量转换方程的斜率:
k0=A·2N-1/Rref
(3)
由式(2)可得电阻的理论测量方程为
Rx=Dx/k0
(4)
将图3中各误差源引入式(1),可通过如下推导得到电路的实际测量转换方程:

(5)
可见Dx与Rx依然可以保持原有的线性关系,但其测量转换方程的斜率和截距却随各种误差因素的影响而发生明显变化。将式(5)改写为标准方程形式:
Dx=k·Rx+b
(6)
则斜率k和截距b与各误差源的关系为:
(7)
图4直观地给出了电路测量转换关系在图3所示误差源影响下的变化情况。

图4 误差源导致的测量转换关系变化情况
如图4所示,被测电阻Rx接入测量电路后,当ADC模数转换输出的数字量Dx=Dout时,若按照式(2)所示测量转换方程进行转换,则被测电阻的测量值应为Rx=Rmeasure,而按照式(6)所示测量转换方程进行转换,则被测电阻的测量值应为Rx=Rcalibrate。由此,可通过以下推导得出从测量阻值Rmeasure到校准阻值Rcalibrate的校正方程:
(8)
令:
(9)
则式(8)所示电阻测量误差校正方程可改写为
Rcalibrate=α·Rmeasure-δ
(10)
式中:α和δ为电阻测量误差校正系数。
将式(3)和式(7)代入式(9),可进一步推导得到校正系数α、δ与各误差源的关系为:
(11)
可见,校正系数α和δ的大小与增益倍数A及其相对误差δA直接相关。因此电路在不同PGA增益档位下的校正系数存在显著区别,有必要对不同PGA增益档位下的校正系数进行分别测定。
图5给出了PGA为Ai增益档位时电路的电阻测量误差校正系数αi和δi的测定原理。在Ai档位下,只需设定Rx=0和Rx=Ri两个不同的电阻标定点,将测量转换结果代入式(6),即可联立求解得到Ai增益档位的电路实际测量转换方程的斜率ki和截距bi。然后将ki、bi以及Ai增益档位的电路理论测量转换方程的斜率(k0)i代入式(9),即可求解得到Ai增益档位的电阻测量误差校正系数αi和δi。

图5 电阻测量误差校正系数测定原理
假设测量电路中的PGA具有A1、A2、…、An共n个增益档位,由于每个档位至少需要包括零点在内的2个标定点才能完成校准,故n个增益档位需要2n个标定点。但由于所有增益档位均包含1个Rx=0的零点标定点,因此只需选择n个基准电阻R1~Rn和1个零点共n+1个标定点即可实现全部增益档位下的自动校准。
校准Ai增益档位所需的基准电阻Ri的阻值应位于Rref/Ai+1~Rref/Ai范围内。选定n个基准电阻后,需通过高精度电阻标定仪器测得所有基准电阻的精确阻值R1~Rn,并通过智能物联网络将其一次性配置入所有待校准的感知节点中。
上述准备工作完成后即可开始电阻测量误差校正系数的测定。感知节点内置有一个工作流程(如图6所示)的电阻测量误差校正系数自动测定程序,可帮助节点实现PGA多增益档位条件下的自动校准。节点整个校准过程主要包括以下3个步骤:
(1)将电路输入端短接,相当于设置公共标定点Rx=0,节点会自动地逐一将PGA的增益配置为A1~An档位,并在每个增益档位下多次采集并计算ADC输出量的平均值(D0)i;
(2)将n个预先选定好的基准电阻依次接入节点,节点会根据接入的基准电阻的阻值Ri自动将PGA增益配置为对应的Ai档位,然后多次采集并计算ADC输出量的平均值DRi;
(3)节点基于图5所示测定原理求解得到A1~An所有增益档位对应的电阻测量误差校正系数α1~αn及δ1~δn,并将其统一存储于节点内置的校正系数数据表中。
由于图6所示程序可根据接入的基准电阻自动选择增益档位并测定出校正系数,校准每个感知节点时,基准电阻无需按增益档位顺序接入,也无需上位机参与增益选档和参数计算,所有校正系数的测定和存储均可由感知节点自身自动完成,由此大幅降低了节点校准的难度和人工干预程度。

图6 电阻测量误差校正系数自动测定程序流程图
完成电阻测量误差校正系数的测定后,感知节点将具备对整个测量范围内的阻值测量结果进行自适应校正的能力,从而可在全量程范围内实现传感器阻值的高精度测量。
当电阻式传感器被接入节点后,节点首先将根据传感器的阻值范围为其自动配置适合的PGA增益档位Ai,从而获得尽可能高的电阻测量分辨力;其次将采用式(4)所示电阻理论测量方程得到被测电阻的理论测量值Rmeasure;最后,节点于内置的校正系数数据表中调取Ai档位对应的误差校正系数αi和δi,然后通过式(10)所示的电阻测量误差校正方程将Rmeasure校正为实际阻值Rcalibrate,从而获得更高精度的电阻测量结果。
3 实验验证
3.1 误差校正系数测定
测量误差校准和评估实验所采用的节点是基于图1和图2所示原理设计的一种面向铂电阻和热敏电阻温度传感器的电阻式传感器智能感知节点。
智能感知节点测量电路中的PGA具有1/2/4/8/16/32/64/128共8档增益倍数,ADC为24位Σ-Δ型ADC。由于Pt100、Pt1000等铂电阻温度传感器的最大测温范围可达-196~600 ℃,NTC-1k和NTC-2k型热敏电阻温度传感器的常用测温范围为-20~160 ℃,欲测量上述电阻式温度传感器,节点的电阻测量范围需覆盖10 Ω~22 kΩ。为此,节点中的参考电阻采用阻值为22 kΩ,精度等级为0.1%,温漂小于±5 ppm/℃的PCF0805-13-22KBT1型金属薄膜电阻。为降低传感器自热误差,激励电流设定为0.1 mA。1 ppm=10-6。
图7给出了智能感知节点测量误差校准系统的示意图。系统包含N个所述感知节点和1个供电节点以及1个网桥节点,所有节点通过一条测控网络线缆连接起来组网工作。其中,感知节点通过开尔文夹具夹持基准电阻以排除线阻的干扰;供电节点可为网络中所有节点提供总线式供电;网桥节点通过以太网与上位机相连,用于配置和采集信息。由于智能感知节点具有自组网测量特性,因此可一次性对多个节点进行校准。
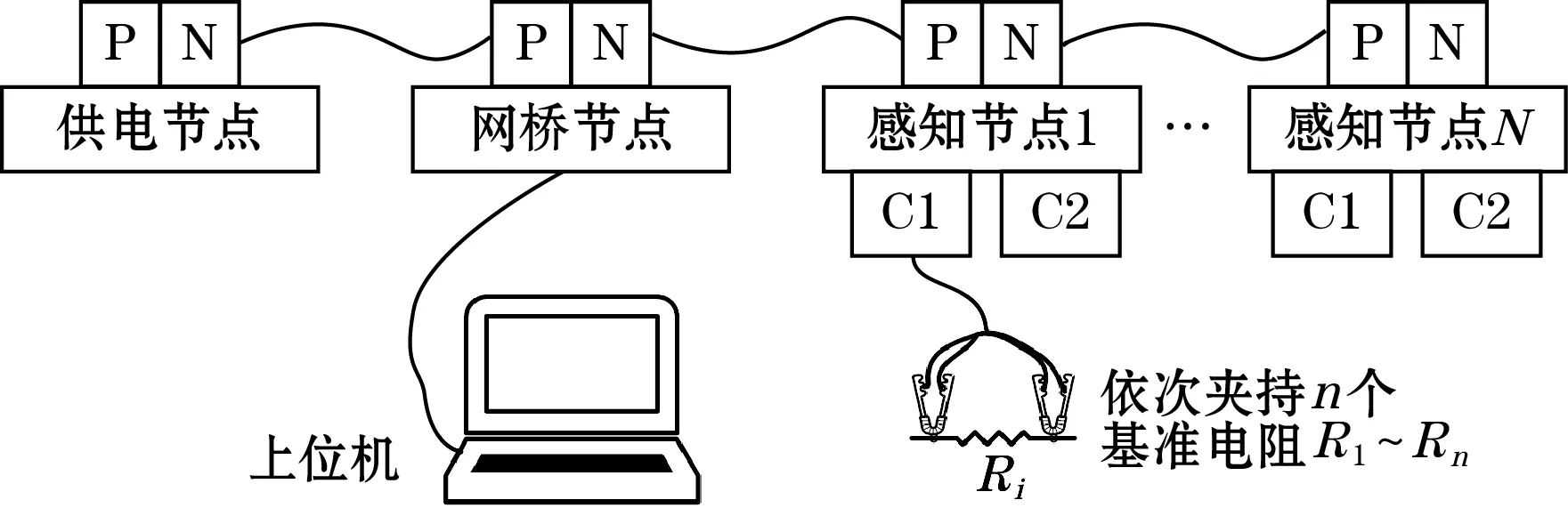
图7 测量误差校准系统示意图
图8为测量误差校准系统的实物图,电阻标定仪器为Agilent-34401A六位半台式万用表。

图8 测量误差校准系统实物图
PGA具有8个增益档位,为每个档位选择了一个温漂小于±5 ppm/℃的EE系列金属薄膜基准电阻,其阻值Ri先由Agilent-34401A标定得到,并由上位机通过图7所示测控网络配置到感知节点内部。
将开尔文夹连接到待校准感知节点的传感器接口上,只需将2个夹子短接1次,随后依次夹持每个基准电阻1次,即可自动完成所有增益档位电阻测量误差校正系数的测定和存储。
表1给出了各增益档位的误差校正系数αi和δi的测定结果。

表1 电阻测量误差校正系数测定结果
3.2 误差校准效果评估
为了进一步验证以上测量误差校准方法对智能感知节点电阻测量精度的提升效果,在节点10 Ω~22 kΩ的电阻测量范围内,另外选取了5个标准电阻10 Ω、100 Ω、1 kΩ、4.3 kΩ、21 kΩ来模拟电阻式传感器,并接入感知节点进行测量对比实验。5个被测标准电阻的阻值散落在整个测量范围内,因此可较好地表征整个测量范围内的测量性能。
首先,采用Agilent-34401A测得5个标准电阻的实测阻值Rstandard分别为9.999 10 Ω、100.023 Ω、999.726 Ω、4 300.17 Ω、21 010.2 Ω,将其作为智能感知节点测量结果的对比基准。
其次,将上述标准电阻分别接入智能感知节点,节点以预先设定的2.5 SPS的测量频率自动完成100次测量,并分别给出校准前的电阻测量值Rmeasure和通过式(10)所示校正方程校准后的阻值Rcalibrate。
最后,通过式(12)计算得到校准前、后的电阻测量绝对误差Δ1、Δ2:
(12)
图9(a)~图9(e)给出了校准前后的电阻测量绝对误差对比曲线,其中横坐标为测量点的序号,纵坐标为节点测量结果的绝对误差。
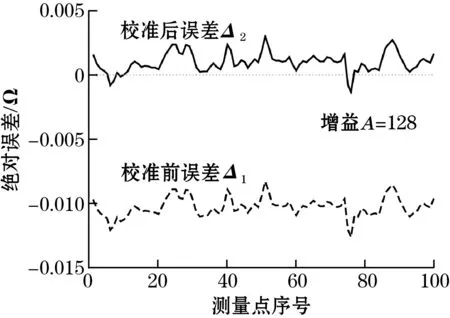
(a)10 Ω标准电阻测量误差
观察图9可知,节点校准后,所有被测标准电阻的测量绝对误差均大幅降低,电路测量精度获得显著提升。由于式(10)所示的电阻测量误差校正方程为线性方程,因此校准前后误差曲线中的波动部分高度相似。
表2给出了对节点上述100次测量数据的统计分析结果。由表2可知,对于全部5个标准电阻,最大测量误差由校准前的-0.1%降低至校准后的0.01%。对于100 Ω、1 kΩ、4.3 kΩ、21 kΩ 4个标准电阻,校准后的最大测量误差仅为0.001%。表2最后一列给出了校准后节点测量结果的绝对误差相对于校准前绝对误差的降低程度,可见校准可使节点测量误差降低90%~99%,能够显著提升电阻式传感器的测量精度。

表2 校准前后的电阻测量结果统计分析表
4 结束语
本文提出了一种增益自动调节型大范围高精度比例式电阻测量电路的测量误差校准方法。该方法中所有增益档位的校正系数的测定和存储均可由感知节点自身自动完成,大幅降低了节点校准的难度和人工干预程度。
节点的电阻测量范围设计为10 Ω~22 kΩ,搭建了节点误差校准系统,并在整个测量范围内选取了5个标准电阻对节点校准前后的测量误差进行评估。实验结果表明:本文提出的误差校准方法可使全部被测标准电阻的测量误差降低90%~99%,校准后节点的测量误差低于±0.01%,足以满足工业现场对电阻式传感器大范围和高精度的测量需求,有望应用于高精度现场测温等智能感知场景。
