多层薄膜的二次电子发射蒙特卡罗模拟研究

彭 敏，程文杰，曹 猛

(西安交通大学 电子与信息学部 电子物理与器件教育部重点实验室，西安 710049)

0 引言

自Campbell发现二次电子发射现象至今已有 120 多年历史，关于二次电子发射的理论及机理研究也经过了长足发展[7-12]。目前,多层薄膜结构实验研究方面进展表明多层薄膜结构样品SEY及其变化趋势与样品的层结构有着很强的相关性。Jokela等[13]利用溅射沉积和移除顶层样品的方法，改变了样品顶层的成分及厚度，实验观测研究了氧化铝(Al2O3)、氧化镁(MgO)、二氧化钛-氧化镁(TiO2/MgO)薄膜表面出射的SEY对表面成分及薄膜厚度的依赖。西班牙马德里自治大学的Nistor等[14]提出的Al基部件镀Ni、镀Ag及化学刻蚀工艺技术，试验结果表明该工艺处理得到的多孔膜层SEY有明显降低。在国内，吴朵朵等[15]在多孔银(Ag)膜结构表面采用了EPLSD法沉积二氧化钛(TiO2)薄膜层，并用化学镀方法沉积了金(Au)膜层，形成了多孔Ag/TiO2/Au膜层，表现出了制备简单、灵活且具有低SEY的优点。

从上述的实验结果不难看出，多层薄膜可以有效影响样品SEY。然而，在已有的文献报道中，对二次电子发射的研究大多基于单层结构，设计特定的陷阱结构以降低材料的SEY。例如，曹猛等[16]建立的二次电子发射多代MC模型，把材料内的电子散射与粗糙表面的多重相互作用一起考虑，模拟了单层矩形沟槽陷阱结构、三角形沟槽陷阱结构和具有高斯统计分布的随机粗糙表面的SEY。二次电子发射的MC模拟鲜少应用于多层结构金属材料样品。

文章首先介绍了多层薄膜二次电子发射MC模拟所基于的理论基础，然后以多层薄膜结构为例研究了二次电子发射MC模型，其中实现要点包括多层薄膜二次电子散射过程、穿过薄膜时受表面势垒的影响和电子运动过程的位置判据，最终得到了多层薄膜平面结构和多层薄膜陷阱结构MC模拟结果，并对多层薄膜平面结构进行了入射角相关性分析。

1 二次电子发射MC模拟理论

二次电子发射现象涉及到的物理机理繁多复杂，涉及到了一系列的复杂物理过程，如电子射入固体、电子在材料内部的散射、激发以及输运等。众多学者采用各种各样不同的方法和模型来研究这一问题并在不同程度上得出了二次电子发射的模拟近似结果，其中MC模拟为经典方法之一。它依靠随机数来进行物理计算和试验，在样本数量足够大的情况下，MC模拟具有很高的计算精度。初始电子发生何种散射、电子在材料内部激发内二次电子过程、内二次电子的出射以及出射真二次电子的数量和角度等二次电子发射现象涉及的复杂过程均是具有一定发生概率的随机事件，因而利用MC方法模拟二次电子发射过程有着充分且合理的数学基础。

多层薄膜二次电子发射MC模拟的关键在于模拟电子在材料内部的散射、激发、输运过程，即电子在材料中的一系列弹性散射、非弹性散射及薄膜穿越过程。多层薄膜可能存在复杂的陷阱结构，因此需要考虑到次级电子的出射和再入射过程，计算出电子每一过程的能量损耗，完整模拟出电子在材料中的运动轨迹。只有穿过最外层薄膜出射的电子才被定义为下一代次级电子。追踪多代次级电子中的每一个电子，直至电子出射或者电子能量在材料内部耗尽，电子被材料吸收。

文中利用Mott截面[17]描述弹性散射过程，并通过介电函数模型计算非弹性散射的截面。Mott截面用于计算不同状态电子发射的弹性散射概率，是Mott于1929年在已有方法的基础上进一步修改完善给出的考虑电子自旋的Mott截面表达式。Mott微分截面由式(1)给出。

(1)

其中|f(θ)|和|g(θ)|表示电子直接散射和自旋翻转散射的振幅，可以由式(2)、式(3)表示。

本次研究以PO2、PCO2、6 min步行实验、术后住院天数、胸管留置时间、胸管引流总量为效果判定指标。6 min步行实验以病房区走廊内的30 m为范畴，要求患者在下午3时到4时之间进步行，并测试步行前后的脉氧、脉搏、血压等指标。同时，以Borg分级方法对胸外科患者的呼吸困难及全身疲劳情况进行评价，共划分为四个等级：1级不足300 m；2级介于300 m到375 m；3级介于375 m到450 m；4级超过450 m。级别越高则说明胸外科患者的心肺功能恢复情况越高，3级或者4级是心肺功能正常的表现。

(2)

(3)

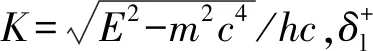
对于电子非弹性散射的模拟，描述电子输运轨迹至关重要。在介电函数模型中，通过介电函数ε(q,ω)描述电子在材料内部的非弹性散射过程，其代表的物理过程是入射电子发生能量损失，引起材料中内层电子或是价电子激发到费米能级之上或电离，内层电子激发需要的能量大于价电子激发。该介电函数最初由Penn[18]提出，由Ding和Shimizu[19]进一步改进发展。电子的非弹性散射微分截面由式(4)给出。

(4)

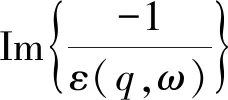
Δs=-λ·lnR

(5)

其中R是均匀分布在0到1之间的随机数，是平均自由程。具有一定能量的次级电子会进一步散射，直到它从表面逃逸出来，或者能量耗尽停留在材料内部而被材料吸收。

电子穿过材料表面的过程模拟需要考虑到表面势垒对电子能量和方向的影响。对于电子发射，它的能量由于材料的表面势垒U0而降低。同时，电子通过材料表面后的弹射方向由式(6)给出。

(6)

(7)

表面势垒对入射电子的影响也作类似的处理。电子能量的增量是U0，方向改变如式(8)所示。

(8)

在多层薄膜二次电子发射的薄膜穿越过程中，原则上电子在出射和再次入射之间的运动会受到材料表面附近局部电场的影响。由于材料界面处材料种类不同，电子排布发生改变而形成该局部电场。这种局部电场本身很微弱，加之实金属材料界面存在随机粗糙度，即非理想情况下的微小凹凸，致使出射和再次入射之间的电子轨迹均满足电场可忽略的情况。但对于半导体和绝缘体材料，表面会积累大量的电荷，达到稳态后，会明显改变初级电子和再入射电子的能量，其影响不能忽略。

2 多层薄膜的MC模拟研究

2.1 多层薄膜MC模型

构建多层薄膜二次电子发射MC模型，首先要构造多层薄膜结构。设定多层薄膜材料输入参数，并在直角坐标系中对X、Y坐标划分若干网格和格点，通过二维矩阵给各个格点赋值即为Z坐标值，并采用反距离加权插值法构造界面。通过多次矩阵输入赋值构造出的多层薄膜默认为无限大，同时不考虑边缘效应。此外，程序中多层薄膜结构的合理性需要验证，即判断电子是否交叉重叠。

多层薄膜二次电子发射MC模拟不仅要考虑材料中的电子散射、电子激发、次级电子的级联过程、次级电子的再入射等过程，还要考虑因输入材料不同电子可能存在的界面穿越或反射。若输入薄膜材料为半导体和金属，则在半导体-金属界面上存在欧姆接触；若程序输入材料均为金属，则不存在电子的界面穿越或反射。整个模拟过程中判定流程如图1所示。初级电子以一定能量和入射角度，进入已构造好的由多层薄膜多种金属材料构成的样品之中，电子在样品中以一定的步长不断散射。电子在材料中运动，其平均自由程与弹性平均自由程、非弹性平均自由程的关系如式(9)所示。

图1 MC模拟多层薄膜二次电子发射过程判定流程图Fig.1 The flow chart of judgment in the SEE process of MC simulation on multilayer thin films

(9)

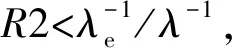
材料中的次级电子输运遵循与初级电子相似的散射过程，MC模拟思想类似于将二次电子发射视为级联过程[20]的输运理论。对于再入射电子的处理与初级电子类似，但穿过最外层薄膜出射再入射的电子，其代际将会增加。对比单层材料二次电子发射MC模型，多层薄膜结构二次电子发射流程最大的区别在于电子在材料内须判定是否发生界面穿越或界面反射。在发生界面穿越或反射时，界面两侧材料不同参数会影响判定结果及后续过程。若电子位置至不同膜层的交界面上时，电子能量大于材料逸出功才有穿越的可能，且须根据随机过程来判断电子能否穿越。

2.2 多层薄膜MC模拟结果

二次电子发射模拟中随机过程众多，要求样本数足够大，文章均设定10000个电子作为初始电子。选取铜(Cu)基片作为衬底，设定Cu-Au-Cu三层薄膜结构，Au 膜和Cu 膜的厚度均为2nm, Cu基片厚度默认为5000nm，其结构示意图如图2所示。模拟电子束单点入射，得到了金属Cu样品和Cu-Au-Cu多层薄膜结构的SEY与入射电子能量的关系曲线，如图3所示。结果表明，多层薄膜影响了二次电子发射过程，在电子初始能量达到400eV之后，多层薄膜有效降低了SEY。需要说明的是，铜基底MC模拟结果较以往实验数据较低，原因在于其非弹性散射截面数据可能存在近似处理误差，但这并不影响采用MC模拟探究该规律性问题。

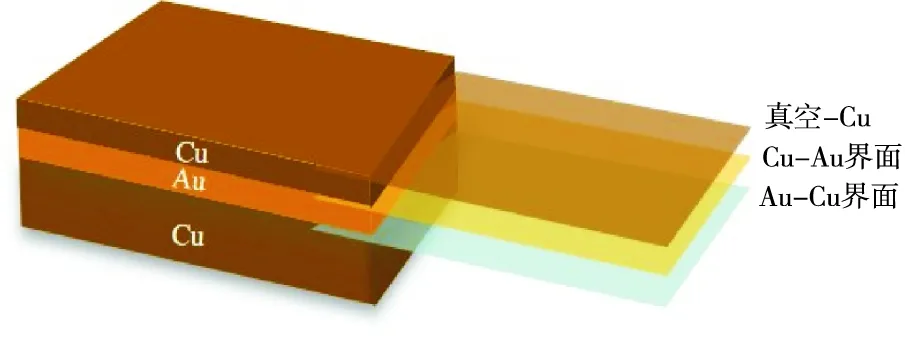
图2 多层薄膜Cu-Au-Cu平面结构示意图Fig. 2 Schematic diagram of the planar structure of Cu-Au-Cu multilayer thin films

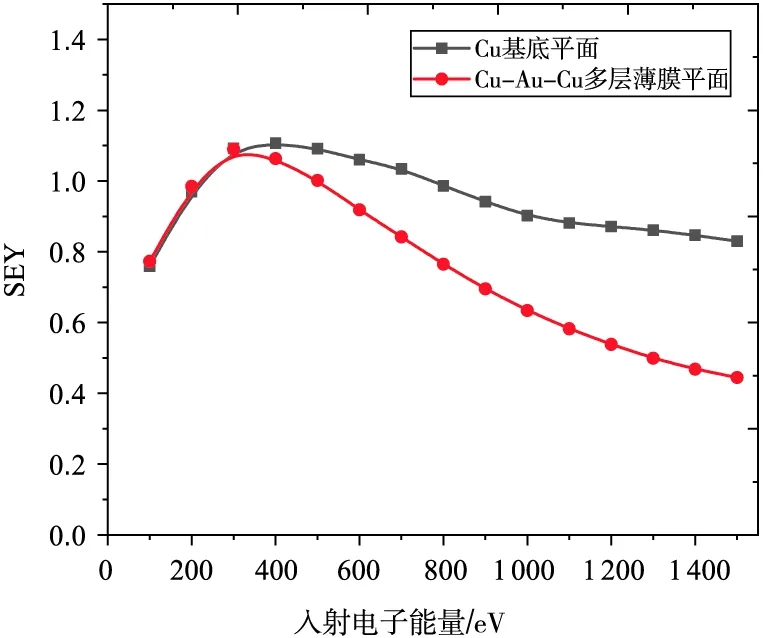
图3 Cu样品和Cu-Au-Cu多层薄膜样品SEY与入射电子能量关系曲线图Fig. 3 The curves between SEY and primary electron energy of Cu and Cu-Au-Cu samples

为探究多层薄膜厚度与样品 SEY 的关系，改变Cu-Au-Cu样品中除基底外的薄膜材料厚度，依次设置Cu-Au两层薄膜厚度分别为5nm和10nm，得到的SEY与入射电子能量关系曲线如图4所示。结果表明，表层Cu薄膜厚度增大到35.4nm时，1500eV以下的入射电子产生的二次电子发射特性与Cu基片趋于相同。原因在于当入射电子能量达到1500eV时，模拟得到的电子最大散射深度是35.4nm。当表层铜薄膜厚度超过35.4nm时，入射电子能量无法使电子穿透薄膜材料，全部的次级电子均由表层薄膜材料产生，因此样品的SEY不再受厚度影响。

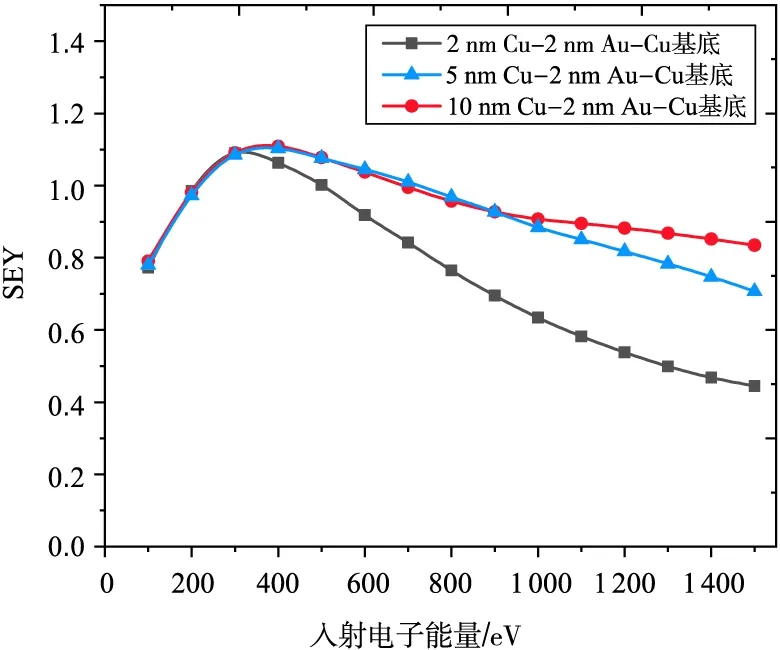
图4 不同厚度Cu-Au-Cu多层薄膜样品SEY与入射电子能量关系曲线图Fig. 4 The curves between SEY and primary electron energy of Cu-Au-Cu samples with different thickness of thin films

在实际工程中，表面陷阱结构被证实能够有效降低样品SEY，故以矩形沟槽为例，研究多层薄膜在矩形沟槽结构中二次电子发射特性。多层薄膜材料的选取须考虑其物理化学特性及成本。Ag的物理化学性能优异，电导率为1.65×10-8Ω·m，其SEY约为1.5。同时，Ag薄膜相比于块体Ag材料成本更低，但因Ag易被氧化，通常有必要在Ag薄膜表面再镀一层Au膜作为保护。Au表面阻抗较低，电导率是2.4×10-8Ω·m，其SEY约1.46，物理化学特性稳定，抗氧化性能优异。因此，模拟Au-Ag-Cu多层薄膜矩形沟槽样品的SEY，其结构示意图如图5所示，设置该矩形沟槽尺寸为d：w：t=1：1：1进行模拟。图6 给出了图5中Au-Ag-Cu多层薄膜矩形沟槽表面和Cu基底平整表面以及Cu基底同尺寸矩形沟槽表面的MC模拟SEY与入射电子能量关系曲线对比图。结果表明，多层薄膜的矩形沟槽结构比其他两种具有更强的次级电子俘获能力。

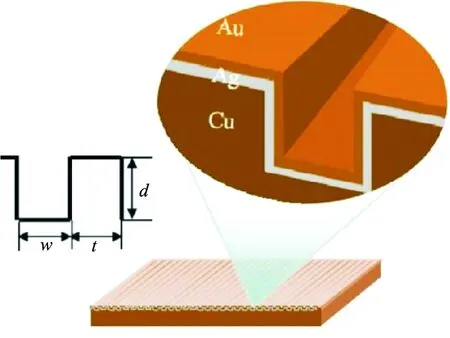
图5 Au-Ag-Cu多层薄膜表面矩形沟槽结构示意图Fig. 5 The structural diagram of rectangular grooves on Au-Ag-Cu multilayer film surface

图6 Cu平整表面、Cu矩形沟槽表面和Au-Ag-Cu多层薄膜矩形沟槽表面SEY与入射电子能量关系曲线对比图Fig. 6 The comparison diagram of the curves of Cu planar surface and Cu rectangular grooves surface as well as Au-Ag-Cu rectangular grooves surface between SEY and primary electron energy

下面研究平整表面多层薄膜二次电子发射的入射角相关性，图7给出了当入射电子能量为600eV时Au-Ag-Cu多层薄膜样品在不同入射角θ下的SEY。多层薄膜的SEY值随着入射电子入射角的增加而增加，这是由于在较大入射角条件下激发的内次级电子更接近于最外层表面而易逸出。

图7 不同厚度Au-Ag-Cu多层薄膜样品SEY与入射角的相关性曲线Fig. 7 The correlation curves between SEY and incident angle of Au-Ag-Cu multilayer thin film samples with different thickness of thin films

图8给出了不同厚度多层薄膜结构的SEY相对增长率比值曲线图。与单层材料Cu相比，当入射角θ较大时，多层薄膜结构的相对SEY会明显大于单层材料。这是由于当入射角θ较小时，多层薄膜结构明显降低了表面SEY，而当入射角θ逐渐增大，电子入射深度变浅而致使其无法穿透薄膜材料，此时次级电子均由单种薄膜材料受激产生，其最终SEY与单层材料基本相同，因而相对SEY会更大。

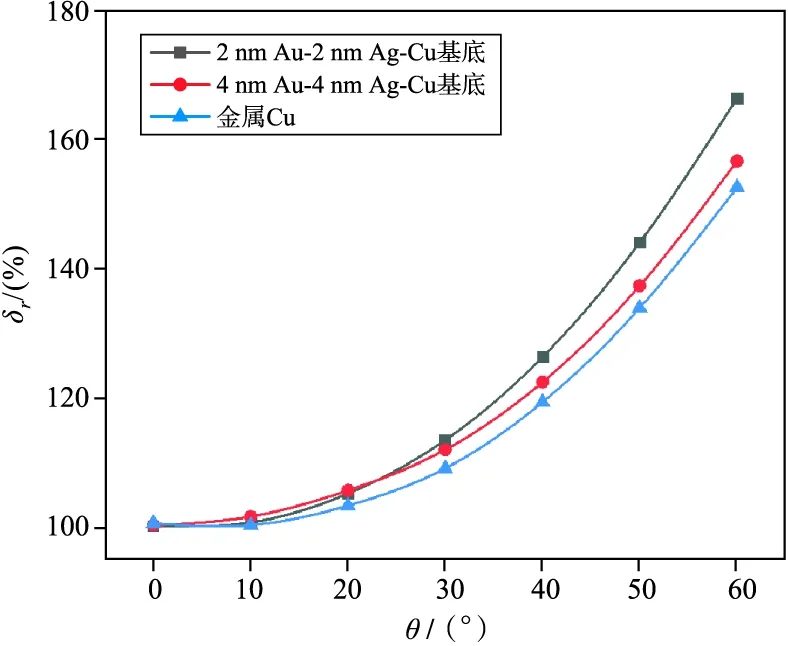
图8 不同厚度Au-Ag-Cu多层薄膜样品的SEY相对增长率比值与入射角的关系曲线Fig. 8 The curves between the relative ratio of SEY growth rate and its incident angle θ of Au-Ag-Cu multilayer thin film samples with the different film thickness

3 结论

基于二次电子发射理论和金属材料复杂表面二次电子发射多代MC模型，构建了多层薄膜二次电子发射的MC模型，实现了对多层薄膜材料的二次电子发射MC模拟，探究了多层薄膜的SEY与多层薄膜厚度之间的关系，并分析了多层薄膜平整表面和矩形沟槽陷阱结构的SEY差异。此外，研究了多层薄膜平面结构中SEY的入射角相关性。通过研究得到以下结论：

1)MC模拟结果表明，多层薄膜的SEY值较基底表面SEY确有降低。MC模拟得到的多层薄膜样品二次电子发射特性曲线与基底金属材料二次电子发射特性曲线分布规律类似，即入射电子能量较小时，SEY随入射电子能量的增大迅速增大；当SEY达到最大值后，SEY随入射电子能量的增加而缓慢减小。

2)在一定厚度范围内，多层薄膜厚度越小，其SEY越低。当表层薄膜厚度增大至入射电子能量不足以使电子穿透薄膜材料入射基底材料时，全部次级电子此时均由薄膜材料产生， SEY不再受膜层厚度增加的影响。

3)陷阱结构和多层薄膜的SEY抑制效果可以叠加，更有效地降低SEY。

4)多层薄膜的入射角相关性与单一基底平面相似。