灌木切割试验装置切割振动分析
2022-09-25薄仕文李耀翔王海滨
薄仕文,李耀翔,王海滨
(东北林业大学 工程技术学院,哈尔滨 150040)
0 引言
灌木作为森林生态系统的重要组成部分,具有不可忽视的经济价值[1-3]。目前,我国灌木切割方式已由传统的人工收割方式向机械化收割发展,主要有小型便携式切割器和大型车载式切割机。切割质量是评价切割机械性能的重要标准[4],而灌木切割过程中产生的振动严重影响了灌木切割质量,进而影响灌木的经济效益。灌木切割装置的振动特性研究对我国灌木机械发展意义重大。
圆锯式切割装置产生振动的主要原因来自灌木切割时的外部激励,外部激励主要为切割时切割平面上受到的切割力与垂直于切割平面刀具受到灌木植株的挤压力。国内外对切割系统进行了大量研究。杨康等[5]设计并优化了秸秆切割器等滑切角刀刃曲线,获取了理论最优滑切角;Chucheep等[6]利用层次分析法进行切割锯片的选择,并得出了最佳方案;Kwon等[7]提出了无支撑灌木切割理论;赖晓等[8]和周敬辉等[9]通过试验研究了液压油缸、发动机和物流架等构件的安装位置对切割系统轴向振动的影响规律。上述研究多为切割器参数优化及在发动机激励下的振动响应,很少涉及灌木切割时所受外部激励作用下的振动响应。
针对上述问题,本文通过对圆锯式灌木切割试验平台的振动理论分析与虚拟振动仿真,研究切割装置在切割时外部激励作用下的振动特性,为后续灌木切割机切割振动理论分析提供参考。
1 整体机构与工作原理
图1为灌木切割设备总体结构图,割灌机主要由龙门架、主体连接轴、调速电机Ⅰ、切割装置、调速电机Ⅱ、固定基架和同步带传动装置组成。同步带传动装置以调速电机Ⅱ为驱动力,电机轴通过联轴器与传动轴相连接,传动轴带动同步带轮转动,同步带从而带动滑块在导轨中行进,以实现整体装置匀速前进且速度可调。切割装置以调速电机Ⅰ为驱动力,锯片通过锯片连接杆与电机轴相连,以实现切割速度可控。
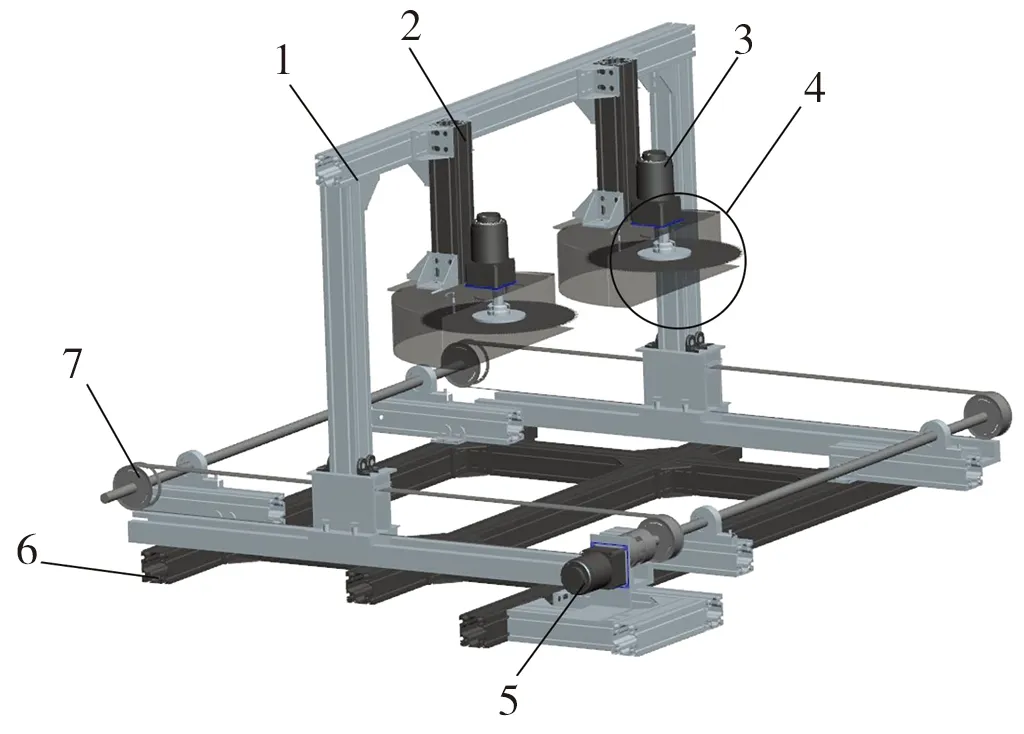
1.龙门架;2.主体连接轴;3.调速电机Ⅰ;4.切割装置;5.调速电机Ⅱ;6.固定基架;7.同步带传动装置。
2 切割装置力学分析
2.1 模态分析理论基础
振动模态是弹性机械结构固有特性[10],可以通过模态分析方法研究切割装置在特定频率范围内的各阶主要模态特性[11-12]。由达朗贝尔原理[13]解算其动力学方程。
(1)
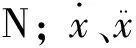
本次模态分析过程中由于分析对象材料为金属,其阻尼非常小,故可忽略其对最终模态分析结果的影响,故取C=0;并且模态分析过程中分析对象无外力作用,取切割装置的等效载荷{F}=0,由公式(1)得到其动力学方程如下。
(2)
切割装置的自由振动可视为简谐运动,其位移矢量矩阵可表示为
{x}={x0}sin(ωt+φ0)。
(3)
式中:{x0}为切割装置的n阶位移向量;ω为位移向量的自振频率;t为切割装置的振动时间;φ0为初相角。
将公式(3)与公式(2)联立解得
(K-ω2M){x0}=0。
(4)
切割装置的刚度矩阵K和质量矩阵M皆为n阶方阵,最终切割装置的n阶固有频率为ωi(i=1,2,3,…,n)。
2.2 振动力学计算
图2为切割装置受力简图。A点与B点分别为锯片连接轴的支撑点;O为锯片圆心点;D点为刃尖,同时也是锯片切割时的受力点,AB段为简支梁,BO段为外伸梁。锯片工作时,受到灌木植株的垂直挤压力、切割力的反作用力等外部激励,均可分解为垂向力和径向力,当在锯片上加装质量块,质量块对锯片的压力FG模拟外部激励在垂直方向分力,质量块产生的向心力FR模拟外部激励的径向分力。
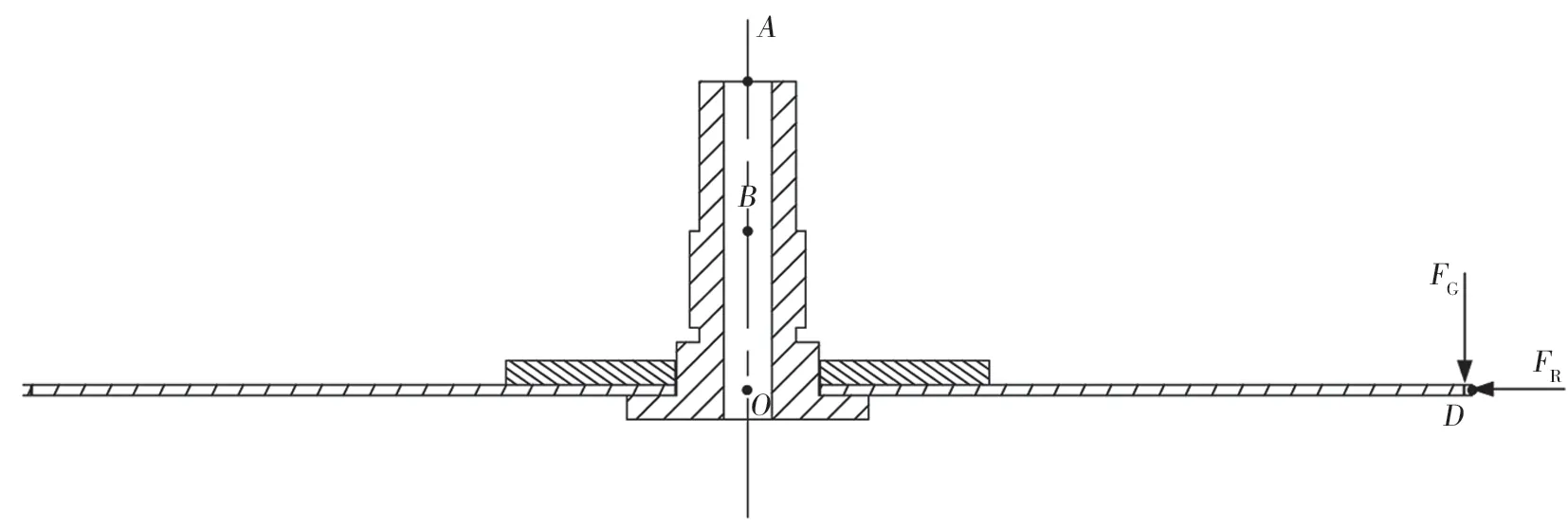
图2 切割装置受力简图
假设模拟质量块的力作用于D点处,只有质量块对锯片的压力FG作用情况下,计算对锯片质心O作用的挠度
τ=mglOD。
(5)
式中:τ为模拟质量块在锯片质心O处的力矩,N·m;m为模拟质量块质量,kg;g为重力加速度,mm/s2;lOD为点O和D间距离,即为锯片半径R,mm,lOD=150 mm。
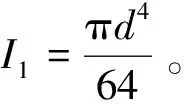
(6)
(7)
式中:I1为简支梁AB的截面惯性矩,mm4;I2为外伸梁BO的截面惯性矩,mm4;d为简支梁AB的直径,mm,d= 20 mm;D为外伸梁BO的直径,mm,D=24 mm。
(8)
(9)
式中:ω1为锯片只在压力FG作用情况下对锯片质心O作用的挠度,mm;θ1为锯片只在压力FG作用情况下对锯片质心O作用的挠角;lBO为点B和O间距离,mm,lBO=28 mm;lAB为点A和B间距离,mm,lAB=31 mm;E为锯片的弹性模量,MPa,取E=2.1×1011MPa。
向心力FR表示为
FR=mRω2。
(10)
式中:ω为锯片转速,r/min,ω=1 350 r/min。
同理,锯片只在向心力FR作用情况下,可计算对锯片质心O作用的挠度ω2和挠角θ2。
由梁的位移叠加原理,可计算出锯片质心O点处的挠度ω0和挠角θ0为
ω0=ω1+ω2。
(11)
θ0=θ1+θ2。
(12)
在锯片高速转动过程中,由于刀盘质心会相对旋转中心产生偏移,会发生动不平衡现象,此时在离心力作用下O点处的挠度ω3和挠角θ3为
FO=m0ω2ω0。
(13)
(14)
(15)
式中:FO为锯片高速旋产生的离心力,N。
则锯片质心O处的总挠度ωt为
ωt=|lOD×sinθ3|。
(16)
因此,可以通过改变模拟质量块质量来模拟不同情况下锯片振动情况,进而研究锯片的振动特性。
3 仿真结果与分析
3.1 振动模态分析
将三维建模软件PRE/O中建立的切割装置模型导入到有限元分析软件ANSYS中,锯片参数见表1。材料设定见表2。

表1 锯片参数

表2 ANSYS材料属性设定
设置材料属性,对切割结构网格进行划分,网格划分时锯片因为结构简单,可选择六面体单元,因此选择三维20节点的solid185号实体单元,切割悬挂梁由于其机构相对复杂,选择六面体会加大计算难度,因此选择三维10节点的solid187号实体单元。共有37 808个节点,划分16 744个网格,最小网格边线长度为3.913 3×10-4m,如图3所示。
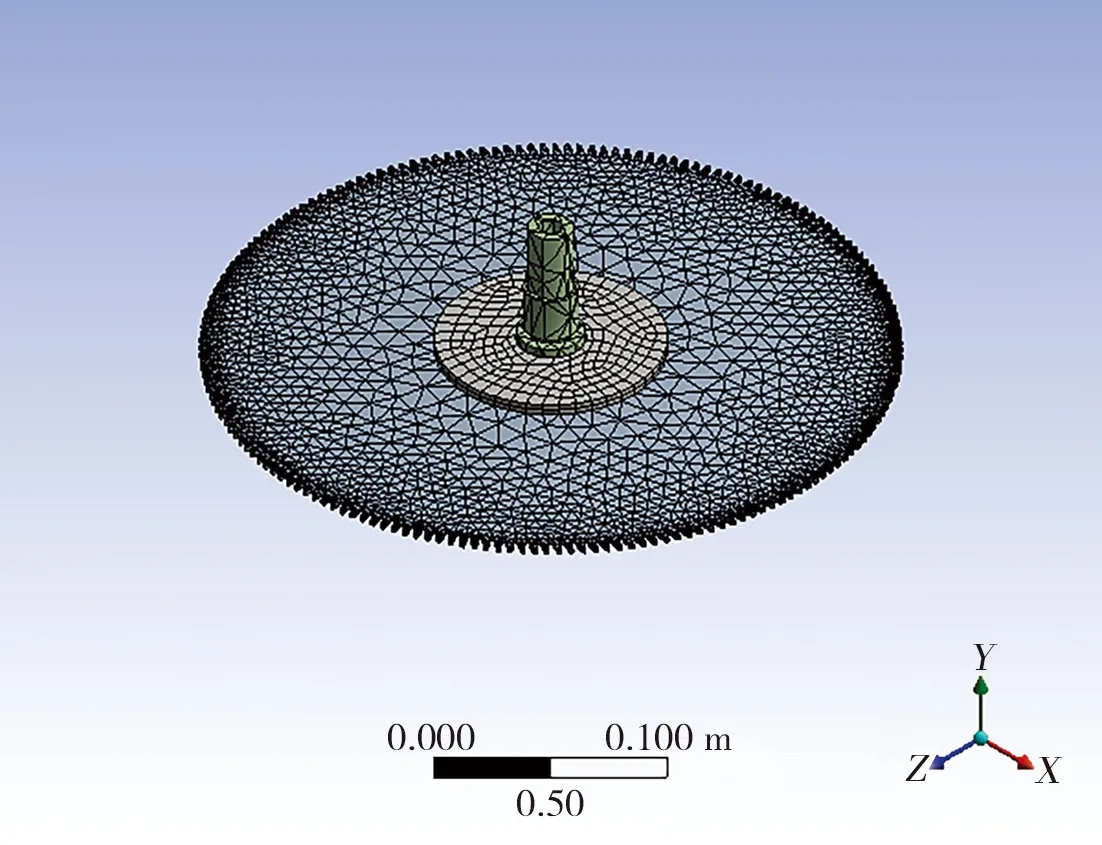
图3 切割装置有限元模型
在ANSYS中采用Block Lanczos法[14-15]对切割装置进行前6阶模态提取,并分析其固有频率和振型。前6阶模态计算结果见表3。

表3 切割装置模态计算结果
前6阶有限元模态分析振型如图4所示。切割结构在第1阶固有频率为1.115 2×10-3Hz,应变幅度为0.610 87 mm,因此可视为无明显振动,如图4(a)所示;第2阶固有频率199.35 Hz处锯片沿Z轴负方向旋转振动,最大应变幅度为1.720 5 mm,与第1阶振型相比巨幅增大,如图4(b)所示;第3阶固有频率200.86 Hz处锯片绕x轴正方向旋转振动,最大应变幅度为1.763 6 mm,且第 2、3阶固有频率接近,如图4(c)所示;第4阶固有频率261.8 Hz处锯片沿Z轴与Y轴叠加弯曲振动,最大应变幅度为1.836 9 mm,与第3阶相比固有频率和振幅出现跳跃增长,如图4(d)所示;第5阶固有频率263.6 Hz处锯片沿Z轴与X轴叠加弯曲振动,最大应变幅度为1.838 9 mm,与第4阶固有频率相比出现小幅度变化,如图4(e)所示;第6阶固有频率347.97处锯片沿Y轴起伏振动,最大应变幅度为1.290 7 mm,如图4(f)所示,随着阶次增加,固有频率也在增大,振型也在不断变化。

图4 切割装置前6阶振型
切割装置作业过程中,其工作频率为
(16)
式中:f0为切割装置工作频率,Hz;n为转速,r/min,n=1 350 r/min。
由公式(16)计算得到切割装置工作频率f0=22.5 Hz,与切割装置前三阶固有频率差距较大,故切割装置结构稳定,不易损坏。
3.2 振动仿真分析
3.2.1 切割装置振动响应分析
为探究切割装置振动特性,对其做受迫振动分析,利用模态频响曲线法分析[16-17],通过施加周载荷观察待测机械结构的位移响应[18]。将切割装置有限元模型导入到动力学仿真软件ADAMS中,利用振动模块,定义全局Z向作用力为输入激励1,作用点为锯片刃齿边缘;定义全局Y向角速度为输入激励2,作用点为锯片连接轴;定义锯片质心点Z向位移响应为输出通道。得出锯片质心位移频率响应曲线如图5所示。切割装置在垂直激励以及旋转激励作用下产生振动,锯片质心在Z向发生位移,在0.01~7.34 Hz时,锯片轴向振幅一直在增大,此过程动刚度减小,振幅在7.34 Hz处达到最大值,激励频率接近刚体动力学固有频率,产生共振,振幅分别为141 mm与56 mm,而后振幅开始下降,缓慢归零。
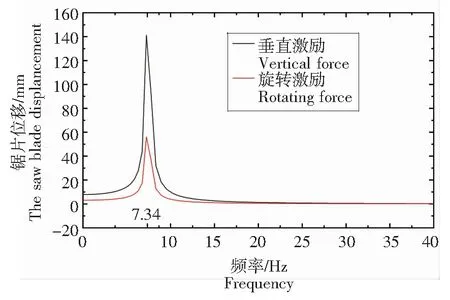
图5 锯片质心位移频率响应曲线
3.2.2 切割力仿真分析
振动会影响切割装置的各个零部件,进而影响切割机械的整体切割性能[19-20],为探究切割装置在外部激励下的振动对切割质量的影响,在有无质量块载荷影响的情况下,利用ADAMS进行切割力仿真,设定质量块的质量为0.2 kg,设定切割装置行进速度为500 m/s,切割转速为1 350 r/min,分析结果如图6所示。切割装置在启动时振动剧烈,需在切割装置运行平稳后进行切割,故将切割装置设置在距灌木植株模型一定距离处。在图6中,切割装置于0.632 s处开始进行切割作业,随着灌木植株材料单元的撕裂,切割力出现波动,当锯片刃尖与灌木截面接触面积最大时,切割力达到最大值,最后归至零。在无外部激励作用下时,切割力在0.68 s时达到峰值,为1 499.8 N;在外部激励作用下时,切割力在0.695 s时达到峰值,为2 011 N,轴向产生的振动幅度大,切割过程与无外部激励情况下相比略显迟滞,切割力最大时间在时间轴上靠后。此时发生的振动容易引起灌木植株发生劈裂现象。外部激励作用下的切割力最大值大于无外部激励作用下的切割力,具体影响还需后续试验验证。
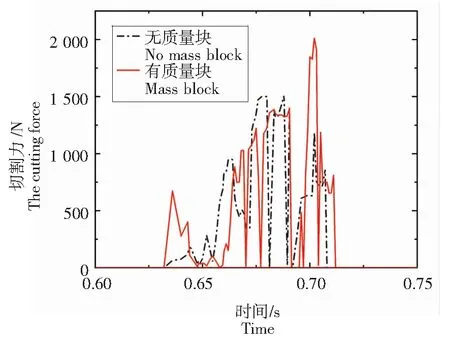
图6 切割力对比时域曲线
4 切割力仿真分析试验
虚拟样机可以在同样的时间内进行更多的试验,有利于初步振动理论的研究[21],因此采用虚拟样机试验法,通过在锯片边缘处添加模拟质量块模拟切割装置作业时所受到的外部激励,以质量块的质量、切割进给为试验变量,以切割力为试验指标,以此探究切割振动对灌木切割时切割力的影响。图7为将Pro/e中建立的灌木切割试验装置的三维模型导入到ADAMS中进行模型优化得到试验装置整体模型。对灌木植株模型进行定义,输入灌木植株各项参数:泊松比为0.3,弹性模量为2.75×109N/m2,密度为540 kg/m3[22]。
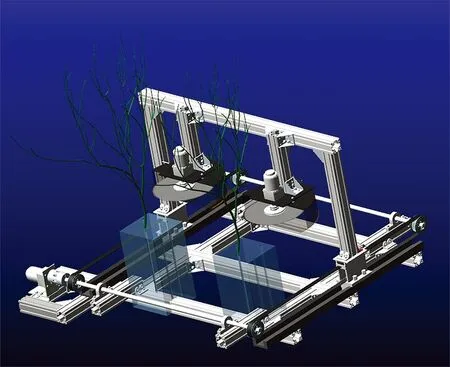
图7 虚拟试验结构图
4.1 锯片振动对切割力的影响
设定切割进给速度为500 mm/s,虚拟样机试验结果见表4。
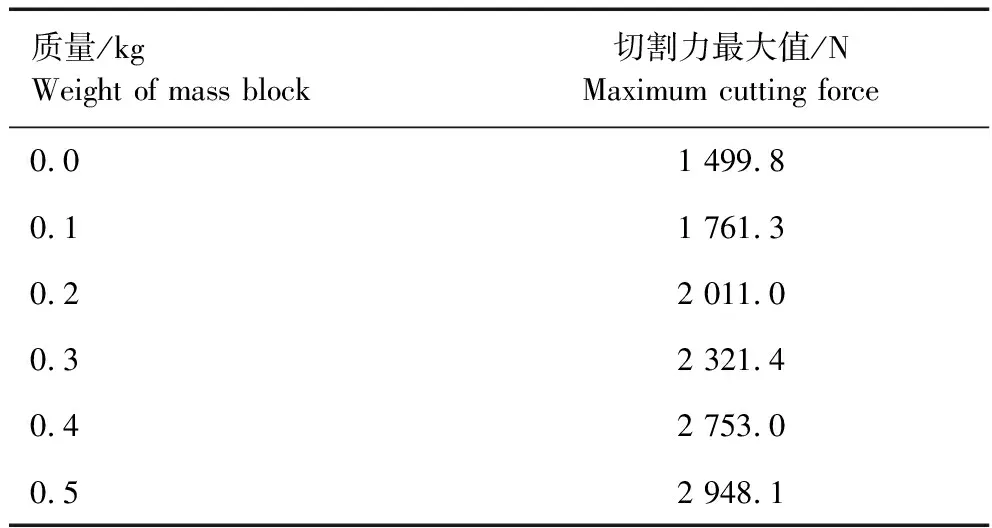
表4 模拟质量试验结果
将模拟质量的虚拟样机试验结果进行回归分析,拟合曲线如图8所示。
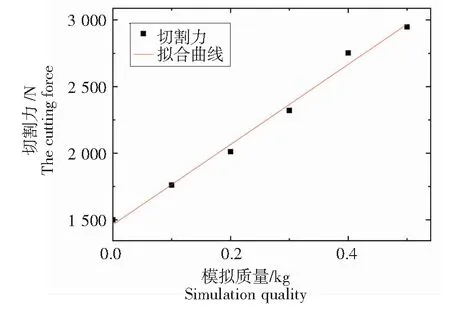
图8 模拟质量试验结果拟合曲线
拟合结果表明,模拟质量与切割力相关系数为0.994,误差为42.9,由此可以得出二者相关性很高并且误差较小,随着模拟质量的增加,即振动幅度的加剧,切割力也随之增大,拟合曲线为y=3 008x+1 464,R2=0.989。
4.2 进给速度对切割力的影响
不考虑模拟质量的影响,将模拟质量设定为0 kg,将进给速度作为自变量,进行虚拟样机仿真试验,试验结果见表5。
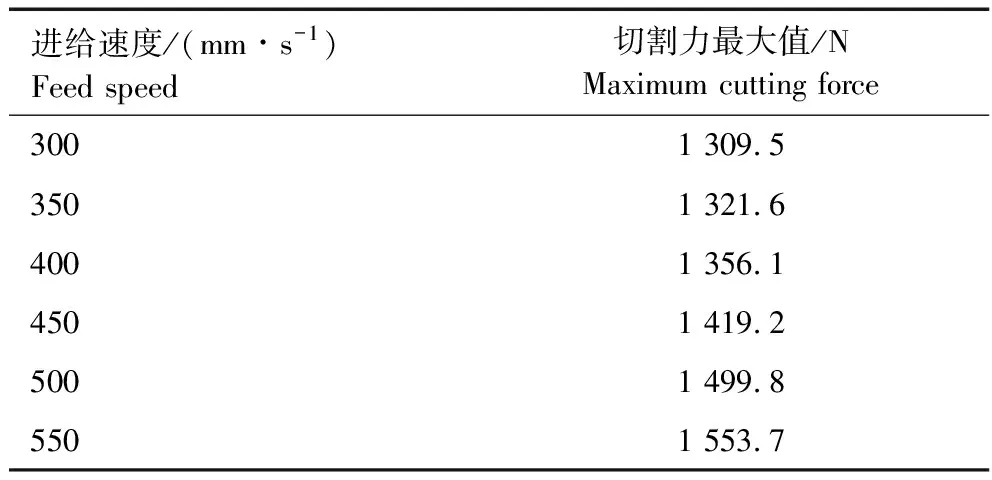
表5 进给速度试验结果
对进给速度试验结果进行拟合分析,如图9所示。
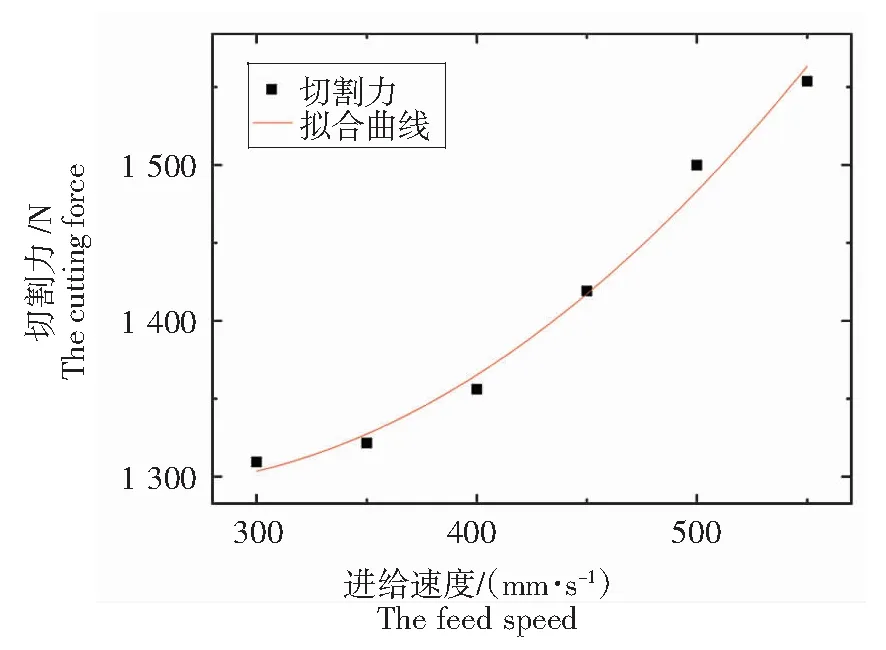
图9 进给速度试验结果拟合曲线
拟合曲线的方程为:y=1 455.365 71-1.349 24x+0.002 81x2,R2=0.982,由此可知在试验范围内,随着进给速度的增加,切割力的最大值也随之增加,这是由于切割灌木时随着进给速度的增加,每齿的进给量也加大,导致锯片与灌木纤维碰撞加剧,进而切割时所产生的切割力变大。
将模拟质量与进给速度拟合曲线对比分析可得,锯片振动对切割力的影响更加明显,因此在灌木切割装置的设计过程中应优先考虑外部激励振动的影响,避免切割时振动对切割质量产生破坏。
5 结论
(1)本文通过在锯片刀盘边缘处安装质量块模拟切割装置工作时受到的外部激励,通过计算证明可以通过加装模拟质量块模拟锯片由于外部激励产生的振动情况。
(2)对切割装置进行有限元模态分析,得出切割装置各阶固有频率以及振型;有无外部激励下对锯片做受迫振动对比分析,得出锯片质心在Z向发生位移,在7.34 Hz处,激励频率接近刚体动力学固有频率,产生共振,振幅分别为141 mm与56 mm。
(3)利用虚拟样机试验法,分析外部激励与进给速度对切割力的影响。结果表明,锯片由于外部激励产生的振动与进给速度均对切割力有着显著影响,且随着模拟质量与进给速度的增大,切割力也随着增大,进而影响切割质量,且模拟质量作为自变量时切割力变化更为剧烈。
