间歇性时间序列的可预测性评估及联合预测方法

郎祎平，毛文涛，2*，罗铁军，范黎林，任颖莹，刘侠

（1.河南师范大学计算机与信息工程学院，河南新乡 453007；2.“智慧商务与物联网技术”河南省工程实验室（河南师范大学），河南新乡 453007；3.株洲中车时代电气股份有限公司，湖南株洲 412001；4.盾构及掘进技术国家重点实验室，郑州 450001）

0 引言

在重型车辆制造、盾构掘进、风电等复杂装备制造企业中，配件的库存价值通常在库存总成本的占比中超过60%［1］。准确的配件需求预测是企业实现产能规划和库存优化的决策依据，也是企业为了提高后市场服务效能、实现全生命周期智能制造的关键环节；然而，在实际业务中，配件计划常与新上线项目挂钩，或与维修现场配件缺失而产生的零星需求有关，导致需求数据的时间序列呈现出典型的间歇性和块状分布，缺乏明确的周期性特点，因而较难以从此类序列中提取充分的波动规律，影响预测效果。如何从间歇性时间序列中提取内在的演化规律，实现准确的序列趋势预测，是当前制造企业配件管理中的迫切需求，同时具有明确的理论研究价值。

目前，间歇性时间序列预测主要基于时间序列预测模型。常用的时间序列预测方法有指数平滑［2］、移动平均［3］等统计学习方法和支持向量回归（Support Vector Regression，SVR）［4］、极限梯度 提升算法XGBoost（Extreme Gradient Boosting）［5］、随机森林［6］和人工神经网络［7］、长短时记忆（Long Short-Term Memory，LSTM）网 络［8］、卷积神经网络（Convolutional Neural Network，CNN）［9］等浅层与深度机器学习模型。此类方法多适用于周期性和趋势性较强的时间序列，对于随机性较强、连续性较差，尤其是样本数较小的间歇性序列，则无法有效提取序列中包含的演化规律，预测结果精度不高。为了实现对间歇性序列的准确预测，一些学者从分析间歇性序列分布特性入手，提出了平均需求间隔（Average Demand Interval，ADI）和变异系数（Coefficient of Variation，CV2）［10-11］等描述间歇性序列的指标，通过挖掘序列的统计特征，实现间歇性序列预测［12-13］。另一种典型做法是对序列进行层次聚类［14-15］，将原有整体规律不明显的序列分为多个具有较显著规律的序列簇，再对各簇选择合适的回归预测算法进行预测。作为代表性工作之一，Shi 等［16］提出BHT-ARIMA（Block Hanker Tensor-AutoRegressive Integrated Moving Average）模型，通过张量分解提取和表示多维小样本序列间的内在相关性，进而使用张量化的ARIMA（AutoRegressive Integrated Moving Average）算法，提取多条小样本序列的公共演化规律，以增加预测模型的信息含量，实现对多条电脑配件序列的联合预测。整体来说，上述方法虽已取得一定结果，但仍存在一定局限：1）只考虑到间歇性序列的统计特征，未能挖掘序列中蕴含的稀疏度、趋势性等其他数据特征；2）多建立在所有序列都具有预测价值的假设上，而忽略了对序列可预测性的细粒度分析。事实上，在企业实际业务中，部分配件一年中仅出现若干次需求，序列数据分布极为稀疏，基本不具有可预测价值，此时在建模中并不适合采用智能预测方法进行走势评估，通常可由人工派单或进行保守备件。

综合上述分析可知，提高间歇性序列预测精度的关键在于：1）如何从不同角度挖掘序列的数据分布特性，定义一个综合考虑多维度信息、具有较好实用性的可预测性度量指标；2）如何有效利用序列间的结构化关系，提高小样本间歇性序列的预测精度。针对以上两点，本文在进行间歇性序列可预测性的分析基础上，提出了一种间歇性时间序列的可预测性评估及联合预测方法。首先，通过统计序列中零需求的频次和位置，并结合最大信息系数（Maximal Information Coefficient，MIC）和ADI，提出了一种新的间歇相似度指标（Intermittent-Similarity，InterSim）；其次，在上述指标的基础上，构建了一个间歇相似度层次聚类方法，进而引入多输出支持向量回归（Multi-output SVR，M-SVR）模型，构建多条序列的联合预测模型，实现对序列间结构化信息的有效利用。本文方法在具有间歇性数据特点的两个公开数据集（UCI 礼品零售数据集和华为电脑配件数据集）和某大型制造企业实际配件售后数据集上进行了对比实验，实验结果证明了本方法的有效性。

本文的主要工作可概括如下：

1）提出了一个面向间歇性序列的可预测性度量指标InterSim。与现有代表性的间歇性度量指标相比，该指标不仅考虑序列自身的稀疏性，同时可有效评估序列的趋势信息和波动规律，从而实现对间歇性序列可预测性的准确量化，具有良好的实用性和普适性。

2）构建了一个基于可预测性聚类的间歇性序列联合预测模型。与现有间歇性序列预测方法相比，该模型可有效选择相似性高、可预测性强的序列，实现对序列预测价值的细粒度分析，并利用序列间的结构化信息提高整体预测效果。根据作者文献调研，目前尚未有基于可预测性的间歇性时间序列预测研究。

1 相关理论

1.1 间歇性特征

ADI和CV2能够很好地描述间歇性需求数据的特点，因此在实际企业业务中常用来对序列分类，依据［11］如下：

1）平稳需求（ADI≤1.32，CV2≤0.49），需求相对稳定，零需求周期较少。

2）不稳定需求（ADI≤1.32，CV2＞0.49），需求不稳定，可变性较大，且需求的发生较为频繁。

3）间歇需求（ADI＞1.32，CV2≤0.49），需求呈现不规则和零星分布，且需求相对较稳定。

4）块状需求（ADI＞1.32，CV2＞0.49），需求模式随机出现，大量时间段没有需求且各个时期的需求之间差异较大，伴随有大量零需求阶段。

1.2 层次聚类

层次聚类是一类常用的聚类方法，主要采用自下而上的凝聚层次聚类或者自上向下的分裂层次聚类方法：最常用的方法为凝聚层次聚类［17］，主要以所有样本作为初始样本簇，依据某种准则合并这些类簇，迭代进行直到将所有数据划分到设定的类簇数目；分裂层次聚类方法［17］则将所有样本初始化为一个类簇，然后依据某种准则逐渐地分裂，直到达到设定的类簇数目。这两种方法的区别在于类间距离的定义不同。由于层次聚类算法存在矩阵计算，因此时间和空间复杂度较高，适用于较小的数据集。通过定义序列之间的相似度指标，层次聚类适合于实现时间序列聚类［17］，同时聚类结果可直观体现序列与序列之间的相关程度。

1.3 多输出回归

多输出回归又称为多输入-多输出（Multiple-Input Multiple-Output，MIMO）问题［18］，指同时对多个输出维度进行回归预测，通过挖掘多条序列之间的结构化关系，提高预测精度和稳定性。多输出回归的核心在于利用输出端之间的相关性信息，弥补小样本回归模型的信息量。人工神经网络具有天然的多输出结构，但通常依赖一定数据量进行模型训练，在小样本回归上容易产生过学习、初始值敏感等问题。而深度神经网络虽然可实现特征自适应提取、进行端到端建模，但同样需要大量数据进行建模。由于实际应用中的间歇性序列通常数据量较小，且数据分布稀疏，小样本特点明显，因此传统神经网络和LSTM 等深度神经网络并不适用于该类序列的趋势预测。相比神经网络，M-SVR 在传统SVR 基础上，引入多个输出维度的统一损失函数，以此实现输出端信息的共享和对序列之间结构化关系的利用，适合于小样本回归预测，因此，本文选择M-SVR 构建多元间歇性序列的MIMO 预测模型，利用多条序列的演化信息，提升联合预测效果。M-SVR 的详细介绍请参考2.2 节。

2 间歇性时间序列的可预测性评估及联合预测方法

本章提出了一种新的间歇性时间序列预测方法，主要包括可预测性评估和多序列联合预测两部分。可预测性评估中，综合多个维度的序列演化规律信息，构建了一个新的间歇相似度指标和对应的层次聚类方法，其作用在于从原始时间序列中剔除极度稀疏、没有预测价值的序列；多序列联合预测旨在利用多条序列的结构化信息进行联合预测，提高小样本下间歇性序列预测效果。本文方法流程如图1所示。

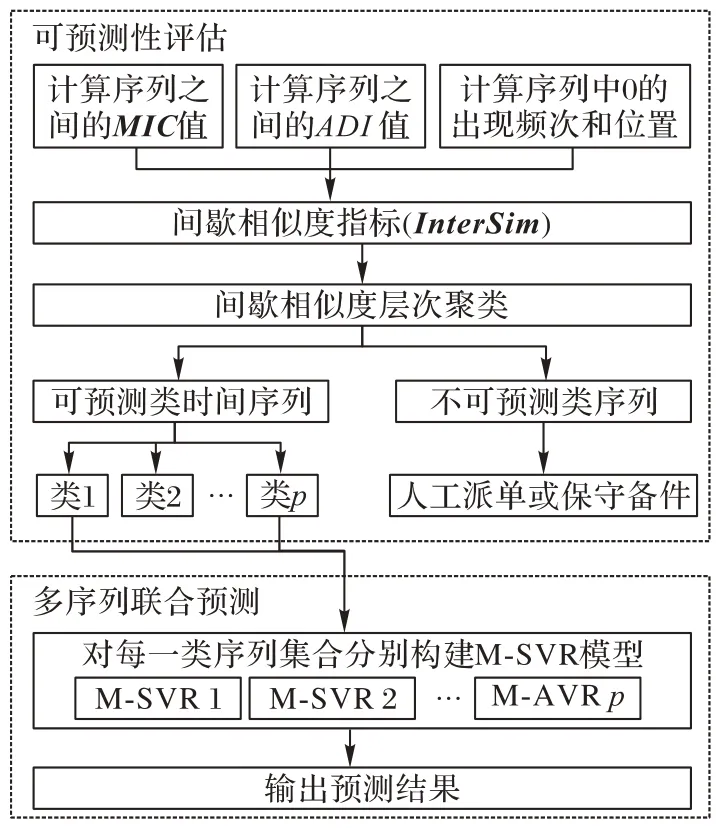
图1 本文方法流程Fig.1 Flowchart of the proposed method

2.1 间歇相似度指标构建

由1.1 节分析可知，现有序列间歇性特征ADI和CV2仅仅统计单条间歇性序列的演化信息，此类信息虽能反映序列的稀疏性，但主要反映的是序列中“0”元素出现的频次，无法体现对应的位置关系，也不足以体现序列的演化趋势，而后者对时间序列预测起到重要作用。为衡量两条间歇性序列演化趋势的相关性，本节引入MIC指标。MIC可有效衡量两条序列的非线性相关性，探索序列间的非函数关系，因此可有效度量序列的演化趋势，具体计算方法见文献［19］。对于间歇性时间序列，MIC无法充分体现出两条序列中关于“0”频次和位置的相似度，换言之，“0”元素将导致MIC计算失真。

此处给出一个算例予以说明。如图2 所示，以序列b为基干序列，通过调整序列中“0”元素的数量、位置和出现频次，得到序列a、c、d。这4 条序列的趋势性和稀疏性各不相同。经过计算序列间MIC可得：1）MIC(a，c)=0.311 2，与MIC(a，b)=1 相比降幅明显，表明序列趋势的变化对于MIC影响较大；2）MIC(a，d)=0.311 2，与MIC(a，c)相同，即“0”元素数量和位置有较大差别的两条序列c和d与序列a的MIC值相同。这表明MIC对于序列中“0”的位置和频次改变并不敏感，有必要在MIC度量基础上进一步引入评价“0”元素出现位置的信息。

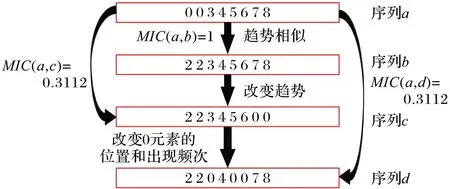
图2 间歇性序列MIC计算示意图Fig.2 Schematic diagram of MIC calculation of intermittent sequences

基于上述分析，本文首先设计了两个指标Zero-Dist和ADI*，用来度量两条间歇性序列中“0”元素位置和出现频次的差异。Zero-Dist(Ti，Tj)实现如下：

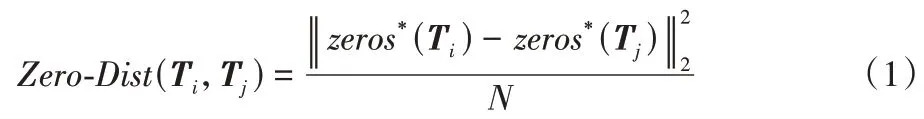
由式（1）可知，Zero-Dist可有效体现两条序列中“0”元素位置的分布差异，若两条序列中“0”元素的位置分布越相近，该值越小；反之，则说明两条序列中“0”元素位置的分布相差越大。此外，考虑到ADI仅适合于统计单条序列中的“0”元素出现频次，本节设计ADI*指标，用以表示两条序列间歇度的差异（即“0”元素出现频次的差异），如下：

其中：ADI(Ti)表示序列Ti的间歇度，k为可变系数。可以看出，两条序列之间的ADI值相差越小，则这两条序列的ADI*值越小。

基于Zero-Dist和ADI*，并结合MIC，构建了一个新的间歇相似度指标（InterSim）。对于给定序列集合T={T1，T2，…，TM}，M为序列个 数，其中第i条序列Ti={xi(1)，xi(2)，…，xi(N)}，N为序列中元素个数，则InterSim如式（3）所示：

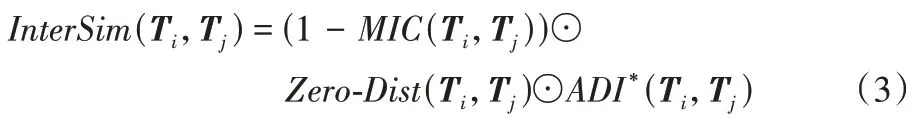
其中：MIC(Ti，Tj)表示序列Ti和序列Tj之间的MIC值，⊙表示哈达玛（Hadamard）积，即矩阵对应位置元素相乘，Zero-Dist(Ti，Tj)表示序列Ti和序列Tj中“0”元素位置的分布差异，ADI*(Ti，Tj)表示序列Ti和序列Tj中“0”元素出现频次的差异。式（3）不仅考虑了两条间歇性序列之间的趋势信息，还兼顾了序列中“0”出现的位置和频次，从而更好地度量序列中间歇度信息和波动规律的相似性。虽然现有ADI和CV2等指标也可表示单条序列的间歇度信息，但并未考虑序列之间的相关性信息，也就无法支撑序列的可预测性。本文提出的InterSim 指标既考虑到了序列间的相关性信息，也提高了方法挑选可预测性序列的能力。InterSim 指标值越小，意味着两条序列之间的波动规律和序列趋势越相似，包含的可预测信息越多。

2.2 间歇性时间序列的可预测性评估及联合预测方法

考虑到间歇性序列的小样本特点，若对单条序列进行预测分析，则模型得到的预测结果精度有限，且易产生波动。本节引入M-SVR，通过对具有可预测价值的序列进行相空间重构，实现对多条序列的联合预测，提高间歇性序列的预测精度。这一思路基于如下假设：对于一个制造企业来说，相关配件序列之间的订货需求存在内在相似性，例如，同一个工程的实施通常需要订购整套的配件，而这些配件之间的序列趋势彼此相关。因此，可同时对多条相关序列联合预测，利用各序列的演化规律信息提升整体预测效果。

首先，利用2.1 节得到的InterSim 指标，采用层次聚类方法，构建了一个间歇相似度层次聚类方法，将序列自适应聚为可预测类和不可预测类。步骤如下。

步骤1 将已知各序列视为一类；

步骤2 利用式（4）计算类簇之间的距离，将距离最近的两类聚合成新类；

其中：1 ≤i，j≤M(i≠j)，A和B表示参与距离计算的类簇A和类簇B，|A|和|B|分别代表对应类簇中的序列数。

步骤3 重复步骤2，直到达到设定的类簇数目。

步骤4 计算步骤3 得到的类簇中每条序列的ADI，并计算每个类簇中的平均ADI值，ADI超过预设阈值的为不可预测类，其余的为可预测类。

其次，对可预测类中的序列，引入M-SVR 构建联合预测模型。由1.3 节中介绍可知，M-SVR 是一种适合做小样本回归的MIMO 建模算法［18］。该方法通过利用多条序列之间的结构化信息，同时提高多个变量序列的预测效果。优化目标如式（5）所示。

综合上述步骤，本节构建了间歇性时间序列联合预测方法如下所示。

输入间歇性序列T={T1，T2，…，TM}，其中Ti={xi(1)，xi(2)，…，xi(N)}，类簇数K，嵌入维度d，时延τ。

步骤1 构建间歇相似度层次聚类方法，实现间歇性序列聚类。

1）将Ti设定成一个类别classi，得到类簇：

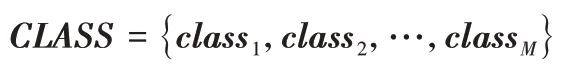
2）从类簇CLASS中寻找距离最短的两个类别classi，classj。距离计算公式如下所示：

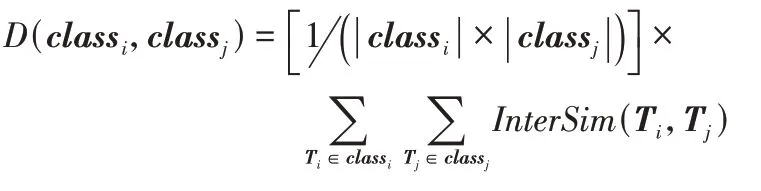
3）将 类classi和classj合并成新 类classn，更新类簇CLASS。

4）若|CLASS|=K，则转入步骤5）；否则转入步骤2）。

5）分别计算CLASS中每条序列的ADI，并计算各类中所有序列的平均ADI值。

6）若平均ADI大于预设阈值，则对应类设为不可预测类CLASS_1，其余的为 可预测类 ：CLASS_2={class1，class2，…，classp}，p+1=K。

步骤2 对于CLASS_2 中每一类序列集合构建M-SVR模型。

1）对CLASS_2 中的序列进行相空间重构。对于第i类classi={Ti(1)，Ti(2)，…，Ti(Li)}(i=1，2，…，p)，则第j条序列重构后的序列为：

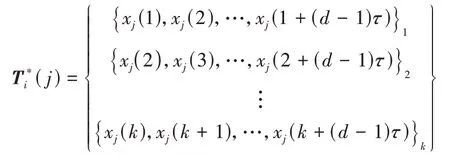
其中k=N-(d-1)τ。

2）构建得到CLASS_2 的重构集合，其中第i类classi的重构序列

3）对CLASS_2 中每一类依次构建单步预测模型。对第i类进行M-SVR 建模，以时间点1 到N的重构数据为输入，以N+1 时间点为输出，构建式（5）所示优化目标，并采用连续迭代的加权最小二乘方法求解，依次得到classi中第j条序列在N+1 时间点的预测结果

输出CLASS_2 中序列第N+1 个时间点的预测值，其中第i类序列的预测结果为

上述方法的复杂度主要集中在步骤1。该部分的复杂度分析主要包括两部分：1）InterSim(Ti，Tj)的计算复杂度；2）基于该指标的层次聚类复杂度。InterSim(Ti，Tj)的计算如式（3）所示，其中1 -MIC(Ti，Tj)的复杂度为O(M2)，Zero-Dist(Ti，Tj)的复杂度为O(M2)，ADI*(Ti，Tj)的复杂度为O(M2)，M为序列条数。在计算InterSim(Ti，Tj)时，将上述三部分的结果进行哈达玛积计算，因此，InterSim(Ti，Tj)的复杂度为O(M2)。此外，由文献［17］可知，基于InterSim(Ti，Tj)的层次聚类复杂度为O(M2)。综上，序列聚类方法的时间复杂度为O(M2)。

3 实验分析

由于本文的实验数据为间歇性数据，序列中包含的“0”元素较多，因此选择均方误差（Mean Squared Error，MSE），平均绝对误差（Mean Absolute Error，MAE）评价方法的性能，计算公式如下：

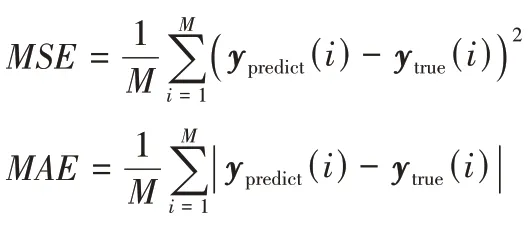
3.1 数据集介绍

为了验证本文方法的性能，在两个公开数据集（UCI 礼品零售数据集［20］和华为电脑配件数据集［16］）进行方法性能测试，并在某大型制造企业实际配件售后数据的需求预测中验证应用效果。数据集详细信息见表1，数据原始分布如图3 所示，图3 及下文各效果图的上方数字均为对应的配件编号。

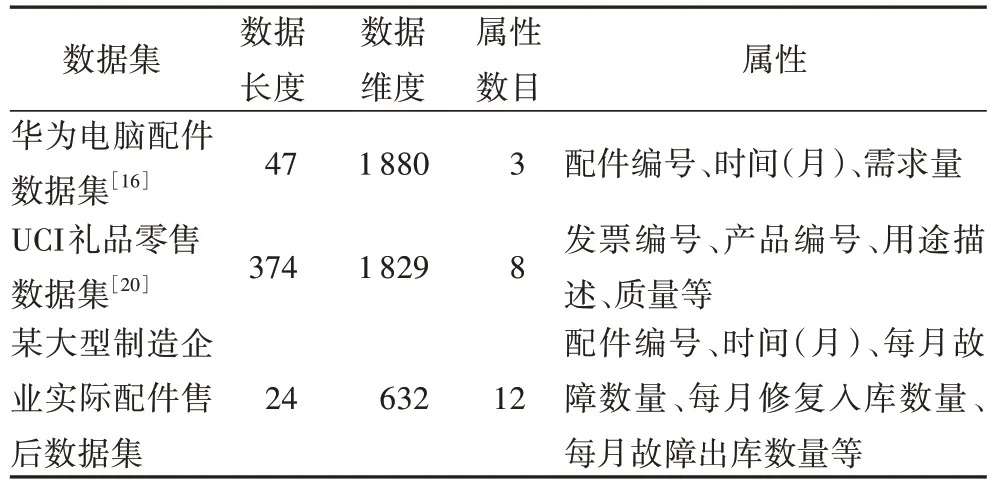
表1 实验数据集信息Tab.1 Experimental dataset information

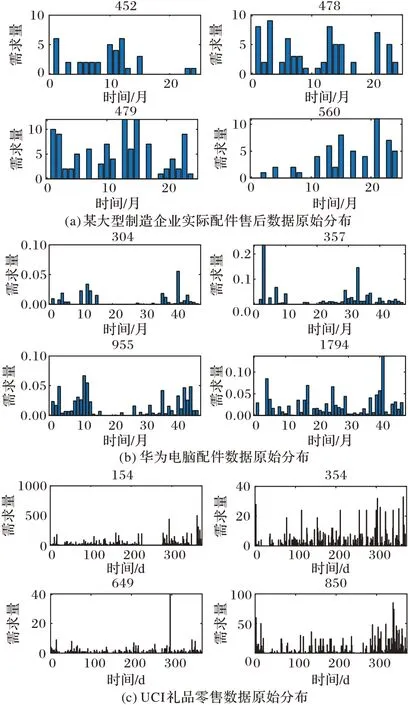
图3 本文实验数据走势分布情况Fig.3 Trend distribution of experimental data in this paper

为直观展现表1 中序列的间歇性分布特点，本节随机挑选出部分序列，并使用间歇性特征指标ADI和CV2展示序列分布特性，具体结果如图4 所示。图4 中两条红线依次表示ADI=1.32，CV2=0.49。根据文献［11］得 到ADI＞1.32，CV2＞0.49，即表示数据呈块状分布特性，意味着序列中大量时间段没有需求、且各个时期的需求差异过大，并伴随有大量零需求阶段。3 个数据集中的序列块状和间歇分布特点明显。尽管如此，部分月份数据的变化趋势仍然存在一定的相似性。

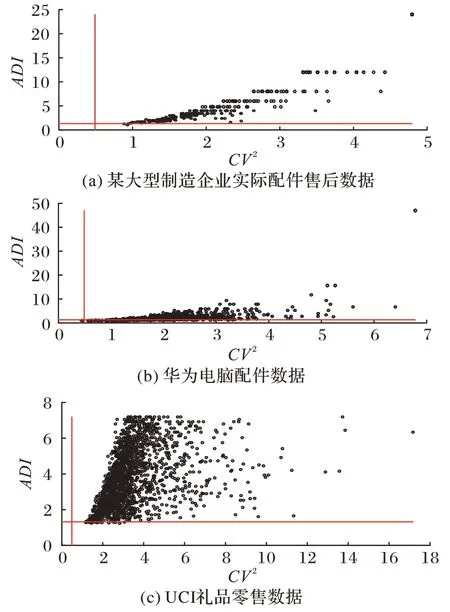
图4 本文实验数据的ADI和CV2分布情况Fig.4 Distribution of ADI and CV2 in experimental data

3.2 对比方法

本文的对比方法既包括传统的浅层机器学习模型，也包括LSTM 等深度模型，同时包括最新的多元时间序列预测方法BHT-ARIMA，如表2 所示。

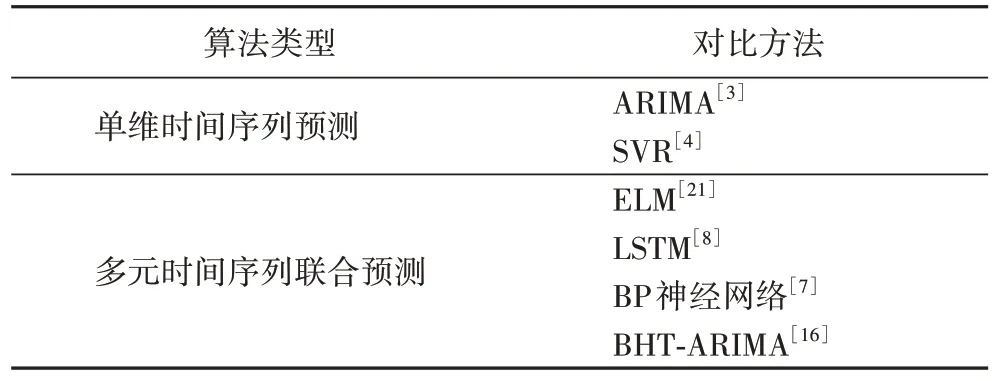
表2 对比方法Tab.2 Comparison methods

实验中，M-SVR 的核函数 为RBF 核函数K(Ti，Tj)=，其核参数为σ，在实验时华为电脑数据集中设置σ=1，UCI 礼品零售数据集和某大型制造企业实际配件售后数据集中设置σ=2-2，正则化参数C为22，松弛变量ε为0.01；SVR 参数和ELM 参数都由网络搜索得到最优；BP 神经网络训练步数为1 000，训练目标最小误差为0.001，学习率为0.01；LSTM 网络设置隐藏层数为100，使用单层网络，学习率为0.01，时间步为5。为消除ELM 和BP 神经网络算法的随机性，预测结果取重复10 次实验的平均值。

3.3 公开数据集的结果分析

采用2.2 节中间歇相似度层次聚类方法对于华为电脑配件数据集和UCI 礼品零售数据集序列进行聚类，聚类结果如图5 和图6 所示。为了便于展示效果，此处仅将序列聚为两类：可预测（A 类）与不可预测（B 类）。可以看出，A 类序列中“0”元素样本相对较少，各个时间点的数据较为密集，序列呈现较明显的演化趋势，因此预测价值较高；而B 类中数据分布更为稀疏，“0”元素时间段较多，数据随机性较高，波动性较大，趋势信息和波动规律表现不够充分，因此将该类序列视为不可预测序列，在进行预测时将其舍弃。

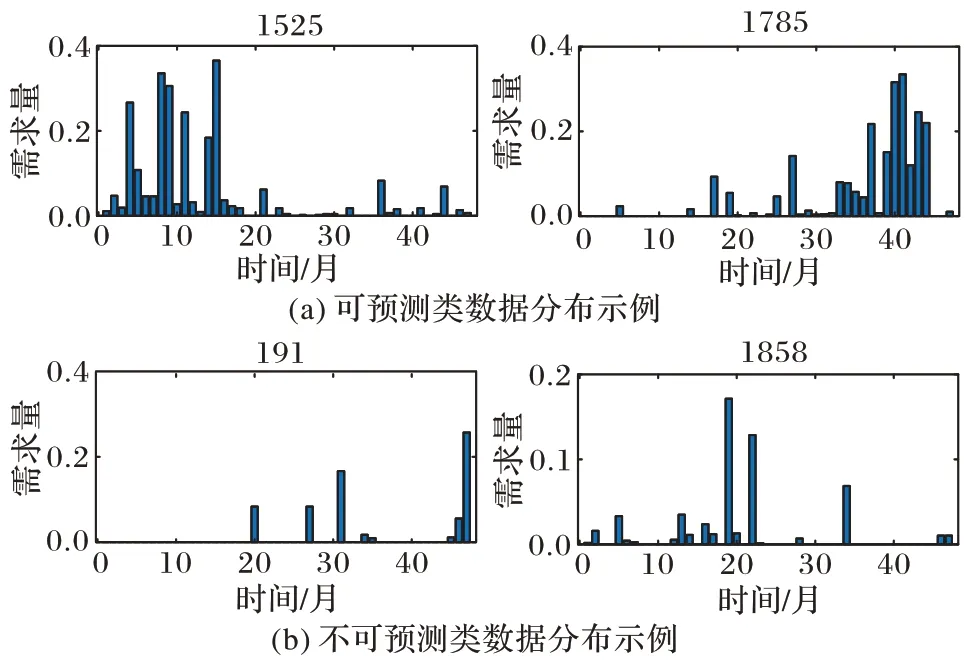
图5 华为电脑配件数据集部分聚类结果示例Fig.5 Some clustering result examples of Huawei computer accessory dataset

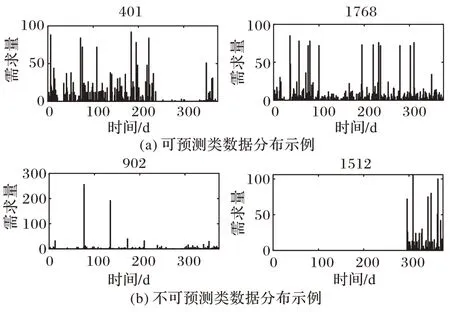
图6 UCI礼品零售数据集部分聚类结果示例Fig.6 Some clustering result examples of UCI gift retail dataset

在序列聚类基础上，对得到的A 类序列进行联合预测建模，不同方法的预测效果见图7 和图8，对应的MSE 和MAE误差见图9。考虑到数据集中的序列长度均较短，在本实验中将华为电脑配件数据集前46 个时间点做训练，预测第47个时间点的需求；将UCI 数据中前373 个时间点做训练，预测第374 个时间点的需求。

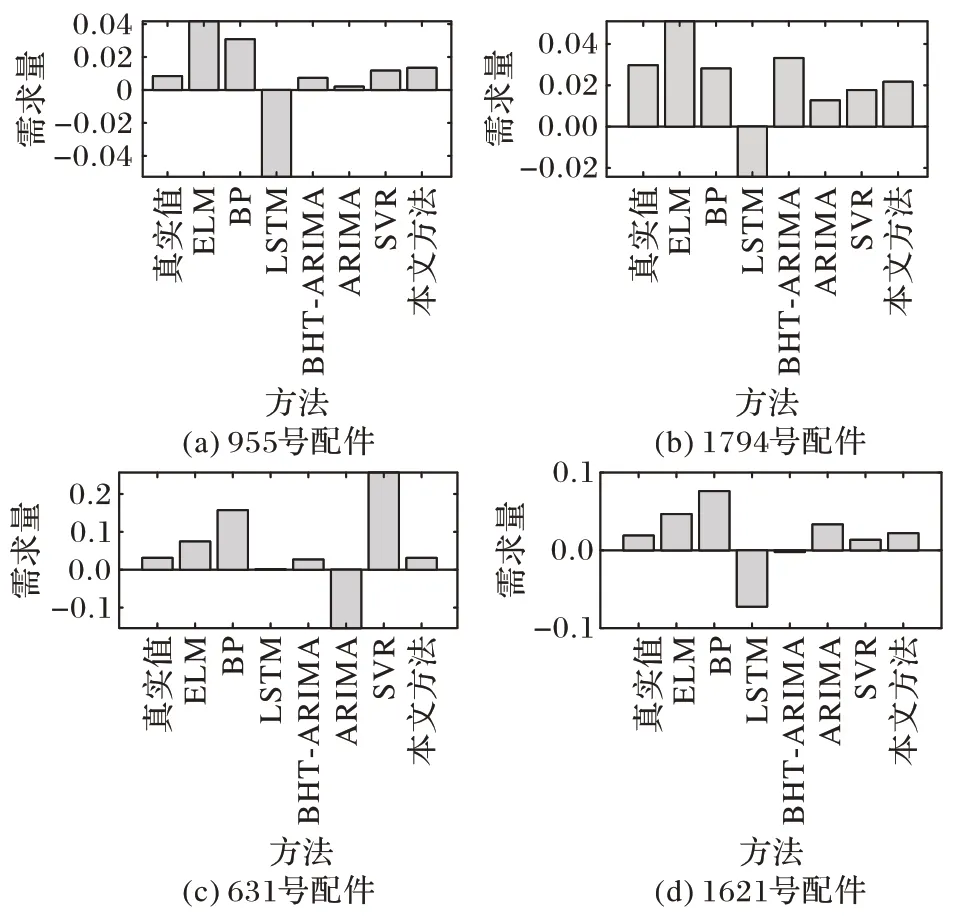
图7 华为电脑配件数据集上不同方法预测结果对比Fig.7 Prediction results comparison by different methods on Huawei computer accessory dataset

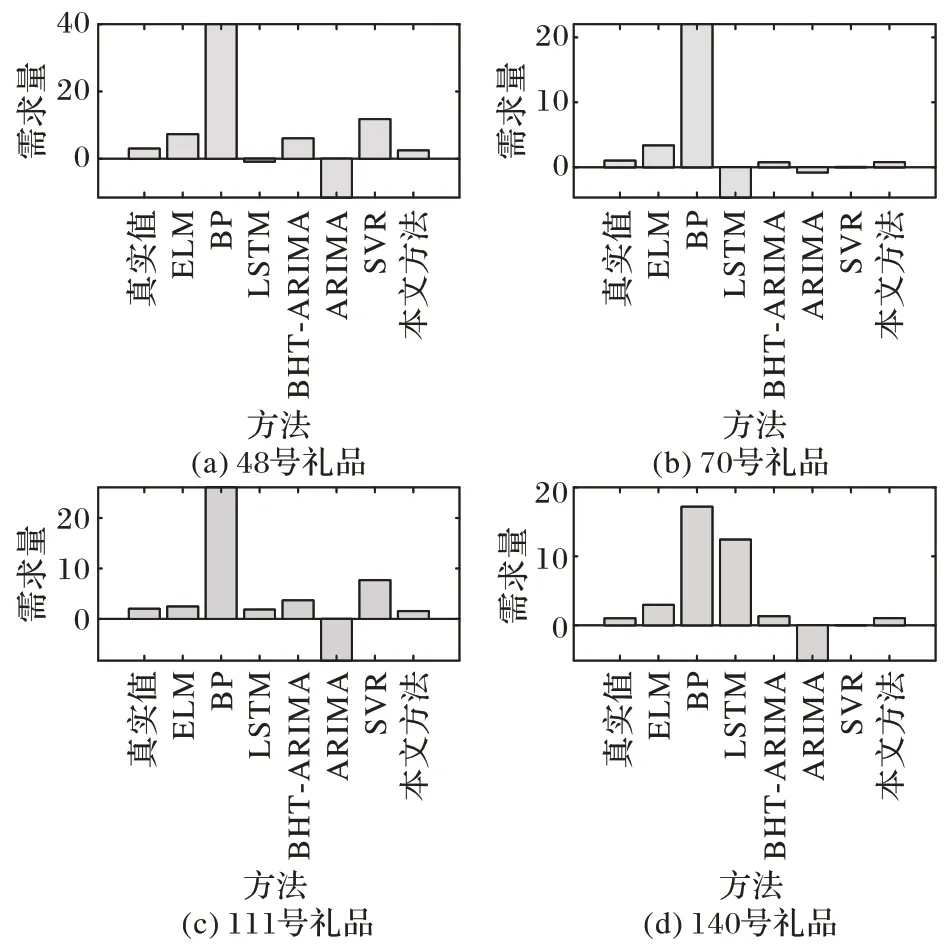
图8 UCI礼品零售数据集上不同方法预测结果对比Fig.8 Prediction results comparison by different methods on UCI gift retail dataset

由图7 和图8 可以看出，对比单条时间序列预测方法ARIMA 和SVR，本文方法预测得到的需求值和真实值更为接近，与多元时间序列预测方法ELM、BP 神经网络相比也取得了更低的误差值，但在部分序列上（例如，图7 中955 号和1794 号），预测误差略高于BHT-ARIMA，图9 同样显示在华为电脑配件数据集上本文方法的预测误差高于BHTARIMA。这是因为BHT-ARIMA 算法适合处理间歇度较小、数据较连续的序列预测问题。此处为了直观展示数据特点对算法的影响，图10 给出了图7 中4 条序列的数据分布，可以看出，图10（a）中，BHT-ARIMA 误差更低的序列更为连续、间歇度更低，而图10（b）中本文方法误差更低的序列的分布则明显更为稀疏。这表明本文方法更适合于预测间歇性明显的序列。

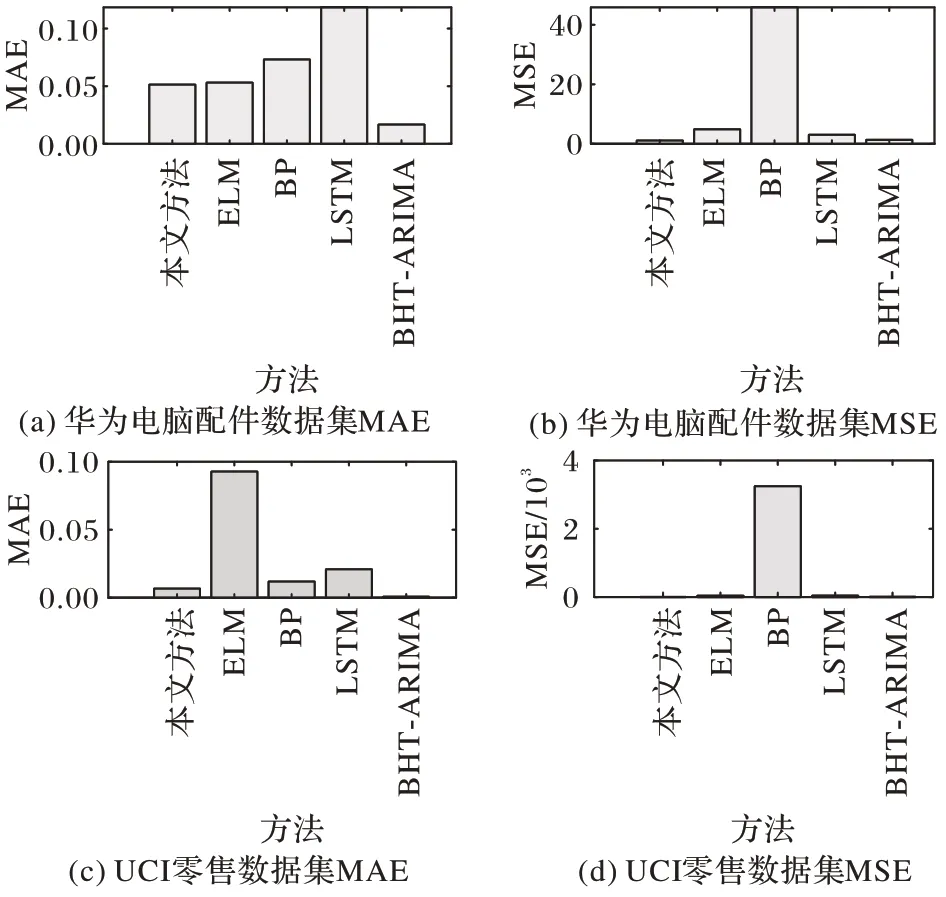
图9 公开数据集上不同预测方法的性能对比Fig.9 Performance comparison of different prediction methods on public datasets

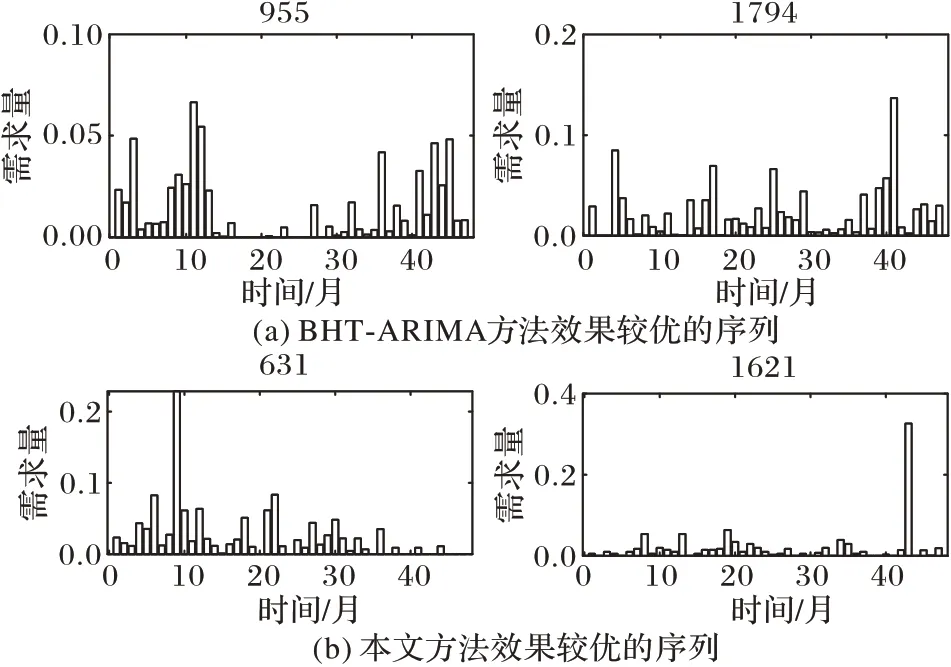
图10 华为电脑配件数据集上结果异常的序列分析Fig.10 Analysis of sequences with abnormal results on Huawei computer accessory dataset

同时，从图7 和图8 中可以看出，SVR 和ARIMA 不仅预测误差较大，后者甚至出现了较多负值。这是因为该两种方法并不适用于对序列长度较短、数据走势波动较大的序列进行预测。而对于ELM 和BP 神经网络这类浅层网络来说，其对数据规模的依赖性较强，但是对于间歇性序列预测，数据量普遍较小，因此，此类算法无法在模型训练过程中学习到充足的数据演化趋势规律，预测误差较大。LSTM 同样存在类似问题。为了进一步探究本文所提方法中参数σ、正则化参数C和松弛变量ε对于方法性能的影响，图11 给出了不同参数取值所对应的MSE，可以看出上述3 个参数对于MSE 的影响在一定取值范围内可保持稳定，但当参数值超过该范围时，则会产生突变。这种变化是由于间歇性序列数据分布零散的特点所致。数据中较大的块状稀疏性使得预测结果只有在部分敏感的参数才会有大的变动，因此，本文所提方法的参数设置较为灵活。在本实验中，在华为电脑配件数据集上设置σ=21，UCI 礼品零售数据集上设置σ=2-2；参数C的设置建议选择C≤22，本文实验中统一设置为C=22；松弛变量ε的设置建议选择C≤2-2，在实验中将ε统一设置为2-2。

图11 公开数据集上不同参数取值所对应的MSEFig.11 MSE corresponding to different parameter values on public datasets

3.4 某大型制造企业实际配件售后数据集结果分析

为了验证本文方法在实际应用中的效果，本文采用某大型制造企业实际业务中配件的售后数据进行实验。图12 展示了聚类结果。可以看出，A 类序列相对于B 类序列来说分布更为密集，趋势信息和波动规律明显，具有较好的可预测性，而B 类中的序列分布极为稀疏。经过与企业沟通，B 类中序列主要是造价昂贵、制作周期较长、需求量较小的配件，可预测价值不高，主要采用紧急派单的方式临时发货，不适用于智能需求预测。这也是本文研究思路的出发点。

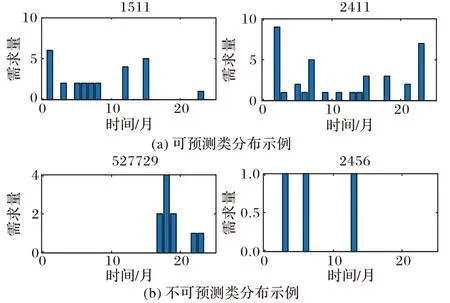
图12 实际配件售后数据集上部分聚类结果示例Fig.12 Some clustering result examples on real-world spare parts after-sales dataset

图13 和图14 展示了M-SVR 模型对于A 类中部分序列的预测结果。可以看出，本方法整体预测效果较为理想。以125 号和1145 号配件序列为例，虽然预测值和真实值存在一定差异，但是由图中预测值的数据走势可以看出，在第24 个时间点的位置，可有效捕捉到序列的下降趋势。此外，需要说明的是，与企业沟通得知，在实际进行备件决策的过程中，预测值和真实值的差异若在[-30%，+30%]，即可视为有效预测。本文预测结果均位于这一区间，由此证明本文方法的有效性。

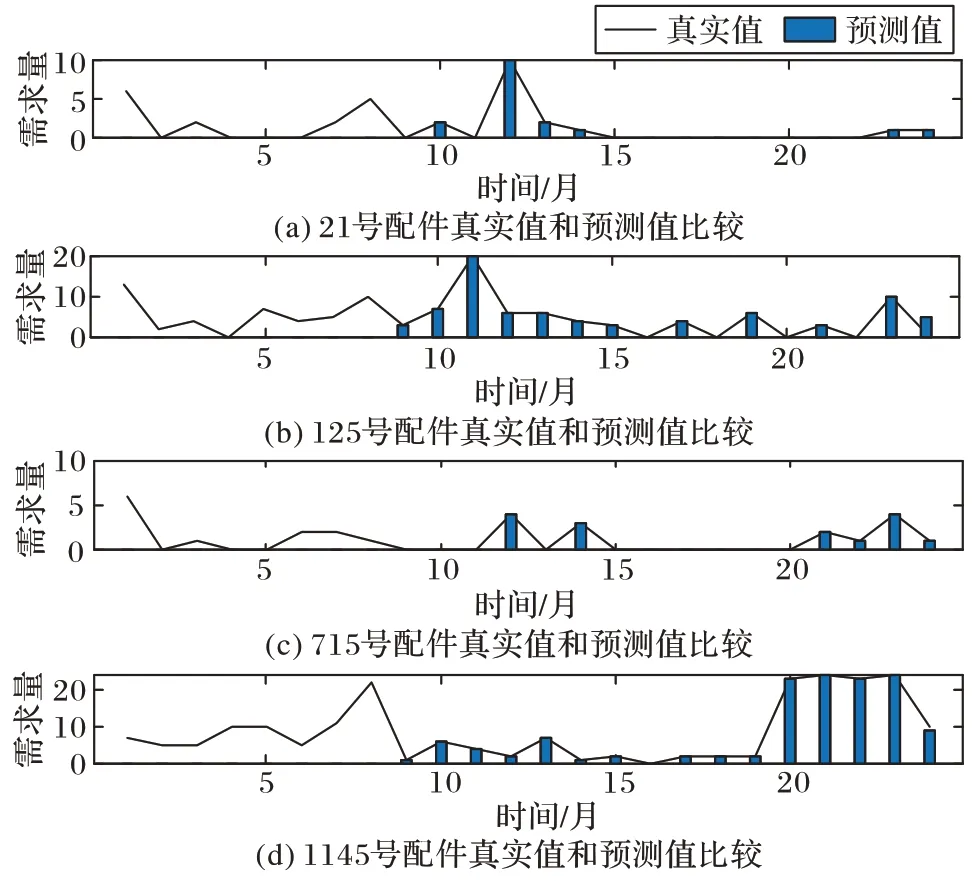
图13 本文方法在21号等配件序列的预测结果Fig.13 Prediction results of the proposed method on sequences such as No.21

图15 给出了对比算法在该企业数据上的预测结果，图16 给出了不同算法的性能。对比单维时间序列预测方法和多元时间序列预测方法，本文方法预测误差明显降低。可以看出，ARIMA 多数预测结果为负值，这与图7 和图8 的结果一致，再次证明了ARIMA 并不适合于间歇性数据的预测。SVR 效果相对较优，这是因为该方法对于预测点附近的值较为敏感，若预测点附近数据分布相对密集（可参见图13 和图14），则SVR 得到的预测结果更为准确，但仍然有部分序列的预测值和实际值相差较大（如1145 号和21638 号）。这从另一方面证明了借助多条序列之间的结构化关系进行联合预测的必要性。对比多元时间序列预测方法，无论是浅层的机器学习模型（ELM、BP 神经网络），还是深度学习模型（LSTM），在该数据上的预测效果都较差。这同样是由于该数据集小样本特点明显所致，上述算法难以从较少的数据量中充分学习到序列的演化趋势信息。虽然BHT-ARIMA 可利用张量分解提取来提取多维序列间的内在相关性，但是由于序列存在较多零需求，最终导致预测误差高于本文方法。

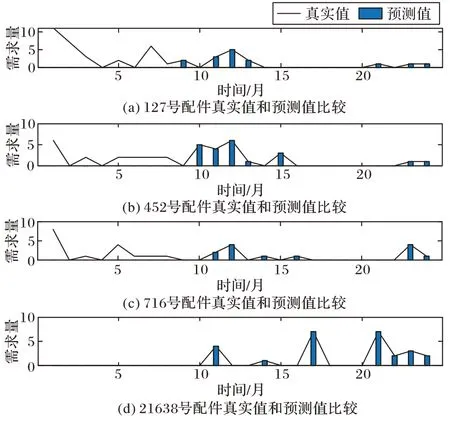
图14 本文方法在127号等配件序列上的预测结果Fig.14 Prediction results of the proposed method on sequences such as No.127

图15 实际配件售后数据集上不同方法预测结果对比Fig.15 Comparison of prediction results by different methods on real-world spare parts after-sales dataset

图16 实际配件售后数据集上不同预测方法性能对比Fig.16 Performance comparison of different prediction methods on real-world spare parts after-sales dataset

4 结语

从间歇性序列可预测分析出发，本文提出了一种间歇性时间序列的可预测性评估及联合预测方法。该方法可有效地从间歇性序列的间歇度差异和演化趋势信息等方面对序列的可预测性进行评估，同时利用序列间的结构化信息进行联合建模，提高小样本下间歇性序列的预测精度。实验结果表明，“0”元素的频次和位置信息对于间歇性序列预测的影响较大，在评估序列可预测性时需要综合考虑序列的稀疏性和趋势性；同时，本文方法能有效预测不同间歇性分布特点的序列趋势，具有良好的实用性，可以满足实际企业的备件要求。

在下一步工作中，我们计划围绕间歇性序列可预测性分析展开进一步研究，通过引入张量，寻找非“0”元素间的低阶演化规律，为可预测性度量提供抽象信息支撑。此外，现实业务中间歇性序列数据量通常较小，因此，采用数据增强技术、扩充有代表性的序列数据同样是我们的关注重点。