结合图自编码器与聚类的半监督表示学习方法

杜航原，郝思聪，王文剑，2*

（1.山西大学计算机与信息技术学院，太原 030006；2.计算智能与中文信息处理教育部重点实验室（山西大学），太原 030006）

0 引言

网络是真实世界中复杂系统的一种存在形式，在日常生活中存在各种网络，如：社交平台中，用户和用户之间关系构成的社交网络；学术网站中，论文和论文之间相互引用构成的引文网络；国家与国家、城市与城市之间运输交通构成的交通网络等。这些网络很好地表达了现实世界物体以及物体之间的联系，分析和研究网络数据具有广泛的学术价值和应用价值，这使得如何从网络数据中学习到有用的信息成为学术界的一大热点［1］。当今世界信息飞速发展，产生的信息网络规模庞大，数据复杂，这对网络研究和分析提出了巨大挑战，而网络研究和分析的有效性，很大程度取决于网络的表示方式。网络表示学习，又被称为网络嵌入，是衔接网络中原始数据和网络应用任务的桥梁，其目的是将网络信息表示为低维稠密的实数向量，从而作为特征输入到后续的网络任务中，如节点分类、链接预测和可视化等［2］。

目前已有的网络表示学习方法从实现手段可以归纳为3 类：1）基于矩阵分解的方法。较早的网络表示学习方法多采用矩阵分解的方式学习网络表示，此类方法以矩阵的形式表示网络节点之间的连接，关系矩阵一般使用邻接矩阵或Laplace 矩阵，利用矩阵分解将高维节点表示嵌入到潜在的、低维的向量空间中，如全局结构信息图表示学习（learning Graph Representations with global structural information，GraRep）［3］、高阶邻近性保持嵌入（High-Order Proximity preserved Embedding，HOPE）［4］、模块化非负矩阵分解（Modularized Nonnegative Matrix Factorization，M-NMF）［5］等方法都是通过矩阵分解生成节点嵌入向量。2）基于随机游走的方法。此类方法利用随机游走来捕获节点之间的结构关系。首先对网络节点进行采样生成随机游走序列，然后用Skip-gram 模型对随机游走序列中每个局部窗口内的节点对进行概率建模，最大化随机游走序列的似然概率，并最终使用随机梯度下降学习参数，从而学习每个节点的网络表示。深度游走（DeepWalk）［6］和node2vec［7］利用不同的随机游走策略捕捉全局或局部的结构信息，并利用Skip-Gram 模型来学习节点嵌入。3）基于深度学习的方法。网络结构复杂多变，并不都是简单的线性结构，此类方法可以提取复杂的非线性网络结构特征，利用深度学习技术学习网络节点表示。结构化深度网络嵌入（Structural Deep Network Embedding，SDNE）［8］、用于学习图表示的深度神经网络（Deep Neural networks for Learning Graph Representations，DNGR）［9］、基于生成式对抗网的图表示学习（Graph representation learning with Generative Adversarial Nets，GraphGAN）［10］采用深度神经网络学习网络嵌入，捕捉到了非线性的结构信息。

早期的研究当中人们将网络表示学习当作一种无监督的过程，关注的是属性和拓扑结构的保持，在现实的网络任务中，节点标签也是一种重要的信息，如节点分类任务当中，节点标签与网络结构和节点属性有很强的相关性，这种相关性在确定每个节点的分类中起着至关重要的作用。继而研究者开始探索如何在网络表示学习的过程中利用标签信息，从而产生了半监督的网络表示学习方法，如图卷积网络（Graph Convolutional Network，GCN）［11］、用数据的转导式或归纳式嵌入预测标签和邻居（Predicting labels and neighbors with embeddings transductively or inductively from data，Planetoid）［12］、可扩展的转导网络嵌入（Transductive Largescale Information Network Embedding，TLINE）［13］等，在进行网络表示学习的同时将已有的部分节点标签信息作为监督信息来指导网络表示的产生，以此获得更优的网络表示。

基于以上问题，本文提出了一种结合图自编码器与聚类的半监督表示学习方法（Semi-supervised Representation Learning method combining Graph Auto-Encoder and Clustering，GAECSRL），利用网络中的部分节点标签来寻求更有效的网络表示方法，主要工作包括：

1）使用图自编码器保持原有网络的结构信息。首先编码器将图编码为低维稠密的嵌入，再通过解码器解码重构原始的图，以此保持原有的网络结构信息；同时利用图神经网络强大的拟合非线性函数的能力捕获高度非线性的网络特征。

2）将图自动编码器和k-means 统一到一个框架中，形成自监督机制。用聚类分布指导网络表示的学习，网络表示学习目标反过来监督聚类的生成，提高网络表示的性能。

3）利用节点的标签信息，指导聚类结果，并增强网络表示的可区分性。

4）在真实数据集上进行节点分类、链接预测，与基准方法结果进行对比分析，实验结果验证了所提方法的有效性。

1 相关工作

1.1 网络表示学习

随着信息技术的发展，信息网络成为人们生活中不可或缺的一部分，分析这些网络可以揭示社会生活中的各种复杂关系，如何捕获网络节点的特征成为网络研究的一个重要任务。网络表示学习的目的就是学习网络节点的潜在、低维表示，同时保留网络的拓扑结构、节点内容和边等其他信息［14］。生成的网络表示可以直接作为节点的特征输入到机器学习任务中，如节点分类、链接预测等，提高网络分析的效率。

给定一个网络G（V，E，X），其中：V表示节点，|V|表示网络G中节点的个数，E表示连接节点的边，X表示节点属性矩阵。网络表示学习的任务就是学习网络数据到表示向量之间的映射函数f，映射函数f保留了原始网络信息，使得原始网络中相似的两个节点在网络表示向量空间中也相似。

1.2 图神经网络

Sperduti 等［15］在1997 年首次将神经网络应用于有向无环图，激发了对有向无环图的早期研究。图神经网络的概念最初由Gori 等［16］提出，并在Scarselli 等［17］和Gallicchio 等［18］的论文中进一步阐述，通过迭代传播邻域信息来学习目标节点的表示，直到达到一个稳定的不动点，这个计算过程非常复杂，最近研究者提出了越来越多的方法来应对这些挑战。经过十几年的发展，近年来图神经网络已成为一种应用广泛的图分析方法。

网络表示学习的目的是将原始网络信息转化为低维向量，其本质问题是学习这个转化过程中的映射函数。一些早期的方法，如矩阵分解、随机游走等，假设映射函数是线性的，然而网络的形成过程复杂，且高度非线性，因此线性函数可能不足以将原始网络映射到嵌入空间。而图神经网络可以为网络表示学习提供一个有效的非线性函数学习模型［19］，将网络结构和属性信息高效地融合到网络表示学习中；同时，图神经网络可以提供端到端的解决方案，在具有高级信息的复杂网络中，利用图神经网络模型的端到端网络嵌入解决方案可以有效分析复杂网络信息［20］。

1.3 图自编码器

Kipf 等［21］于2016 年提出了变分图自编码器（Variational Graph Auto-Encoder，VGAE），还提出了一种不变分的图自编码器，自此开始，图自编码器（Graph Auto-Encoder，GAE）凭借其简洁的Encoder-Decoder 结构和高效的编码能力，在很多领域被广泛应用。图自动编码器的基本思想是：首先输入网络的邻接矩阵A和节点的特征矩阵X，然后通过编码器学习节点低维向量表示Z，再利用解码器重构网络。图自编码器由于其使用的非线性映射函数能捕捉网络的高度非线性结构，与大多数现有的用于节点分类和链接预测的无监督网络表示学习模型相比，图自编码器具备较强的网络表示能力。

2 结合图自编码器与聚类的半监督表示学习方法

为了同时保持网络的标签信息、结构信息和属性信息，本文提出了一种结合图自编码器与聚类的半监督表示学习方法（GAECSRL），该方法的框架如图1 所示，该方法包括图自编码器模块、自监督模块和半监督模块3 个部分。首先，利用图自编码器生成网络表示；然后，在生成网络表示的基础上，将图自动编码器和k-means 统一到一个框架中，形成自监督机制，用聚类分布指导低维嵌入的学习，嵌入目标反过来监督聚类的生成；最后，在网络表示学习过程中使用标签信息来监督图自动编码器的训练过程，使具有相同类别标签的节点具有相近的低维向量表示。

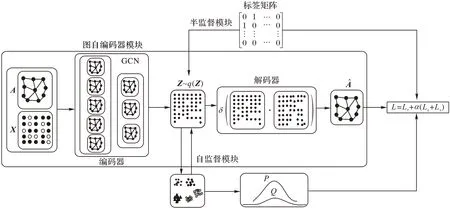
图1 结合图自编码器与聚类的半监督表示学习框架Fig.1 Framework of semi-supervised representation learning combining graph auto-encoder and clustering

2.1 模型结构

给定一个图G（V，E，X）且节点个数为|V|=N，邻接矩阵A表示节点和节点之间的连接关系，矩阵X表示节点特征。

图自编码器模块 使用图自动编码器得到网络的低维向量表示，将邻接矩阵A和特征矩阵X输入到图自编码器中，通过编码器编码可得到低维表示Z。网络表示Z可由式（1）计算得到：

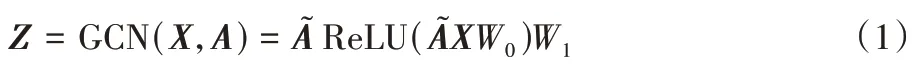
解码器采用简单的内积得到重构的邻接矩阵：

图自编码器的主要工作就是利用图神经网络将网络数据逐层降维，最终投影到一个低维潜在空间中从而达到数据降维的目的。图自编码器使用GCN 作为解码器来学习潜在的网络表示，将网络的邻接矩阵和特征矩阵输入到GCN 中，GCN 每层神经网络之间的激活函数起到了将“线性”转化为“非线性”的作用，这使得图自编码器可以很好地捕捉到网络中的非线性结构，经过GCN 中多层神经网络的层层编码得到最终的网络表示；然后将学习到的网络表示作为输入，输入到内积解码器中解码得到重构邻接矩阵，构建损失函数，通过迭代最小化损失优化图自编码器，使得重构的邻接矩阵与原始邻接矩阵尽可能相似，从而得到最优的网络表示。

自监督模块 将图自编码器和k-means 结合起来，统一到一个框架中，有效地对两个模块进行端到端的训练，使它们相互促进、相互监督，形成自监督机制。

将网络表示输入到k-means 中进行聚类，对于第i个样本和第j个聚类，使用学生分布来度量数据表示zi与聚类中心向量μj之间的相似性：

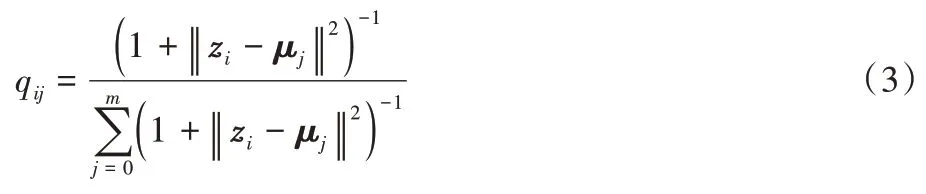
其中：zi是嵌入Z的第i行，μj在预训练图自编码器学习的表示上用k-means 进行初始化，qij可以看作是将样本i分配给聚类j的概率。在得到聚类结果分布Q后，通过学习高置信赋值来优化数据表示。

目标分布P由分布Q确定：

在目标分布P中，Q的每个任务都被平方并标准化，使任务具有更高的置信度。由于目标分布P是由聚类结果分布Q定义的，所以聚类的效果影响着网络表示的生成，而网络表示的优劣是聚类结果可信的关键，在不断迭代更新的过程中，可信度高的聚类结果使得网络表示更优，更优的网络表示又导致更好的聚类效果，从而达到自监督的目的，最终使学习到的网络表示保留更多的网络信息，与原始网络相似度更高。

半监督模块 GAECSRL 方法设计了一个标签矩阵来保存网络的类别信息，将标签矩阵记为B=[bij]。标签矩阵定义如下：

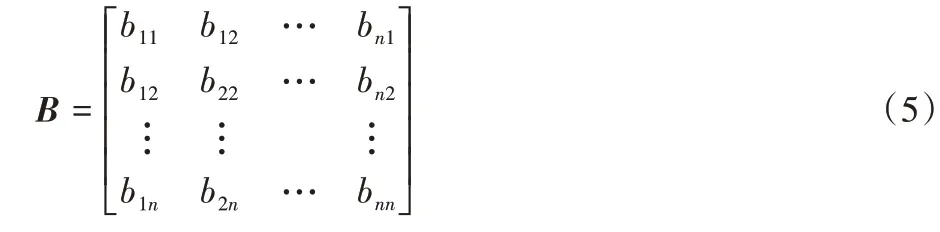
对于任意两个节点vi和vj：若有同一个类别标签，bij被赋值为1；否则，bij被赋值为0。如果不知道节点vi或节点vj的标签信息，bij也被赋值为0。

在现实网络中，节点通常具有监督信息，即节点类别标签。标签信息在许多任务中都起着积极作用，例如节点分类。然而，采用无监督的方式学习网络表示模型，忽略了节点的类别属性。GAECSRL 将网络中少数的真实标签利用起来，监督网络表示的学习，提高了网络表示的可区分性。

2.2 模型优化

GAECSRL 方法的最终目标函数如下：

其中：Lr、Lc和Ls分别是重构损失、聚类损失和半监督损失，超参数α＞0。

重构损失函数Lr采用交叉熵作为损失函数，直观上来看，合适的网络表示能使重构出来的矩阵与原始矩阵尽可能相似。损失函数采用如下的形式：

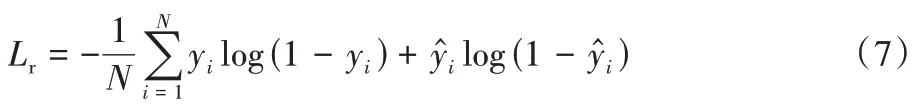
其中：y是原始邻接矩阵A中的值（0 或1）是重构邻接矩阵中的值（0 到1 之间）。

自监督模型的目标函数Lc如下：

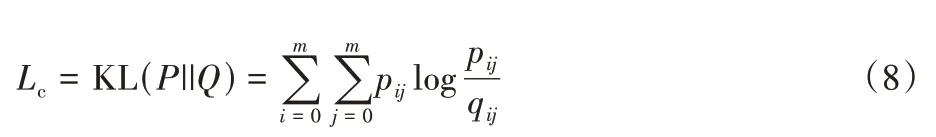
通过最小化Q分布和P分布之间的KL 散度（Kullback-Leibler divergence）损失，目标分布P可以帮助图自编码器模块学习到更好的聚类任务表示，监督Q的更新，又因为目标分布P是由分布Q计算出来的，而分布Q反过来监督分布P的更新，这种相互监督机制就是自监督机制。在相互促进的过程中生成的网络表示更有利于后续任务的进行。

在潜在表示空间中，期望具有相同标签的点之间的距离更近。半监督模型的目标Ls定义为：

半监督损失Ls代表网络表示｛zi｝与先验信息B的一致性，最小化半监督损失可以最小化违反约束的代价，从而能学习到符合指定约束的特征表示。如果zi和zk属于同一类，则zi和zk在潜在空间Z中的距离较小，使来自同一类的节点更加接近。通过这种使用先验信息以某种方式纠正不适当的网络表示，使网络表示的结果更优。

在训练过程中，使用随机梯度下降（Stochastic Gradient Descent，SGD）和反向传播对簇中心μ和网络表示Z进行同步更新。分布Q在训练过程中监督目标分布P的更新。由于目标的不断变化会阻碍学习和收敛，在每次迭代中都用Q更新P会导致自训练过程的不稳定性，因此设置了一个迭代间隔M，每M次迭代更新一次P，以避免上述可能出现的不稳定性。

每个数据点zi的梯度计算公式为：

在空间Z中，每个簇中心μj的梯度由式（11）计算得到：

在反向传播过程中，通过传递梯度L/zi来更新图自编码器的参数，梯度L/μj通过SGD 更新聚类中心。在达到最大迭代次数时，停止算法。

综上所述，GAECSRL 流程如算法1 所示。

算法1 结合图自编码器与聚类的半监督表示学习方法。

输入 原始网络G，邻接矩阵A，特征矩阵X，节点类别数K，标签集D，最大迭代次数MaxIter，目标分布更新间隔M。

输出 网络表示Z。

3 实验结果及分析

3.1 数据集

为了验证GAECSRL 方法的有效性，选取了一些基本方法在真实数据集上通过节点分类和链接预测任务与该方法进行对比。

在实验中使用了以下4 个不同规模的真实数据集：Cora、CiteSeer、PubMed、Wiki。

Cora 数据集包含2 708 份科学出版物表示的节点，分为7类。引文网络由5 429 条表示引文关系的边组成。每个出版物的特征由一个1 433 维向量编码。

CiteSeer 数据集包含来自6 个类和4 732 条边的3 312 个出版物。每条边表示两份出版物之间的引用关系。每个节点表示出版物，每个节点的特征用3 703 维向量表示。

PubMed 引文网络由19 717 篇科学论文和44 338 个链接组成。每个出版物特征都用500 维向量描述，并分为3 类。每个节点表示一篇科学论文，每条边表示一个引用关系。

Wiki 数据集由2 405 个文档组成，分为19 个类，它们之间有17 981 条边。每个节点表示一个文档，一个节点特征向量有4 973 维。

数据集的详细统计信息如表1 所示。

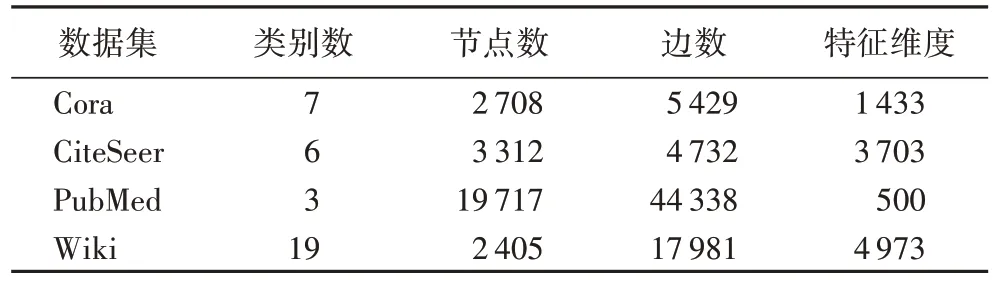
表1 数据集的统计信息Tab.1 Statistics of datasets

3.2 对比方法

实验过程中选取了DeepWalk、node2vec、GraRep、SDNE、Planetoid 作为对比方法验证GAECSRL 的有效性。

DeepWalk 是一种无监督的网络嵌入方法，它分为随机游走和生成表示向量两个部分。首先利用随机游走算法（Random walk）从网络中提取一些节点序列；然后借助自然语言处理的思路将生成的节点序列看作由单词组成的句子，所有的序列可以看作一个大的语料库；最后利用自然语言处理工具word2vec 将每一个节点表示为一个维度为d的向量。

node2vec 是一种无监督网络嵌入方法，它扩展了DeepWalk 的采样策略。它结合广度优先搜索和深度优先搜索，在图上生成有偏置的随机游走，保持了图中的高阶相似性，同时广度优先搜索和深度优先搜索之间的平衡可以捕获图中的局部结构以及全局社区结构。

GraRep 是一种基于矩阵分解的无监督网络嵌入方法，使用不同的损失函数来捕获不同的k阶局部关系信息，利用奇异值分解（Singular Value Decomposition，SVD）技术对每个模型进行优化，并结合从不同模型中得到的不同表示来构造每个节点的全局表示。

SDNE 是一种基于深层神经网络的网络表示方法。整个模型可以被分为两个部分：一个是由Laplace 矩阵监督的建模第一级相似度的模块，另一个是由无监督的深层自编码器对第二级相似度关系进行建模。最终SDNE 算法将深层自编码器的中间层作为节点的网络表示。

Planetoid 是一种半监督的网络表示学习方法，它扩展了随机游走方法，在嵌入算法中利用节点标签信息。联合预测一个节点的邻居节点和类别标签，类别标签同时取决于节点表示和已知节点标签，从而进行半监督表示学习。

3.3 评价指标

在本节中，对数据集进行节点分类、链接预测，以评估提出GAECSRL 方法性能。采用Micro-F1 和Macro-F1 作为节点分类的评价指标，AUC（Area Under Curve）作为链接预测的评价指标。

基于二分类问题可为每一类都建立如表2 混淆矩阵，其中：真正例（True Positive，TP）表示将正类预测为正类的个数，假反例（False Negative，FN）表示将正类预测为负类的个数，假正例（False Positive，FP）表示将负类预测为正类的个数，真反例（True Negative，TN）表示将负类预测为负类的个数。

表2 混淆矩阵Tab.2 Confusion matrix

根据矩阵，可计算出第i类的精确率（Precision，P）和召回率（Recall，R），如下所示：

F1 的计算公式如下：

1）Macro-F1。

对各类别的精确率（P）和召回率（R）求平均：

再利用F1 公式计算出来的值即为Macro-F1：

2）Micro-F1。

先计算出所有类别的总的精确率P和召回率R：

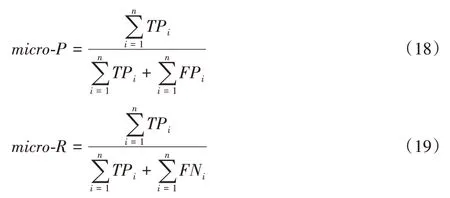
再利用F1 公式计算出来的值即为Micro-F1：

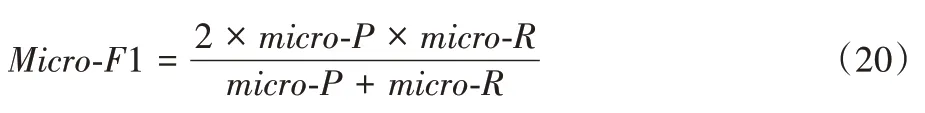
3）AUC。

ROC 曲线下的面积被称为AUC，是评估算法预测能力的一项重要指标。分别结算模型结果的“真正例率”（True Positive Rate，TPR）和“假正例率”（False Positive Rate，FPR），将TPR作为纵坐轴，FPR作为横坐轴作图，即可得到ROC 曲线。TPR和FPR的计算公式如下：

AUC的计算公式如下：

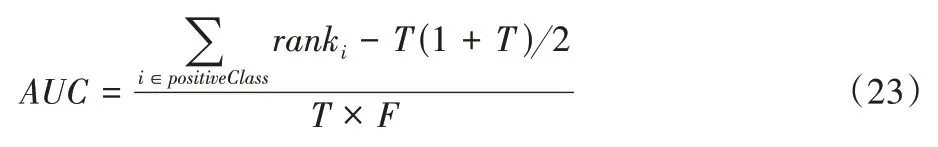
首先将得分从小到大排序，然后只对正样本的序号相加，并减去正样本之前的数，最后除以总的样本数得到AUC。

3.4 实验结果与分析

为了验证方法的有效性，在4 个真实数据集上分别通过节点分类和链接预测任务来评估GAECSRL 和对比方法的性能。在实验中随机抽取一部分标记的节点，并将它们的表示作为特征进行训练，剩下的用于测试，在训练中将标记节点比率从10%提高到90%。使用3 个小型网络Cora、CiteSeer和Wiki 以及1 个大型网络PubMed 来评估所有方法的性能。节点分类任务中采用Micro-F1 和Macro-F1 作为评价指标，链接预测任务中采用AUC 作为评价指标。对于所有方法，分别运行每种方法10 次，节点分类任务产生的平均Micro-F1和Macro-F1 如表3 和表4，链接预测任务产生的平均AUC 如表5。实验以PyTorch 为框架，网络表示空间维度设置为10。下面对GAECSRL 和基线方法产生的实验结果分别进行分析比较，最好的结果用粗体显示。

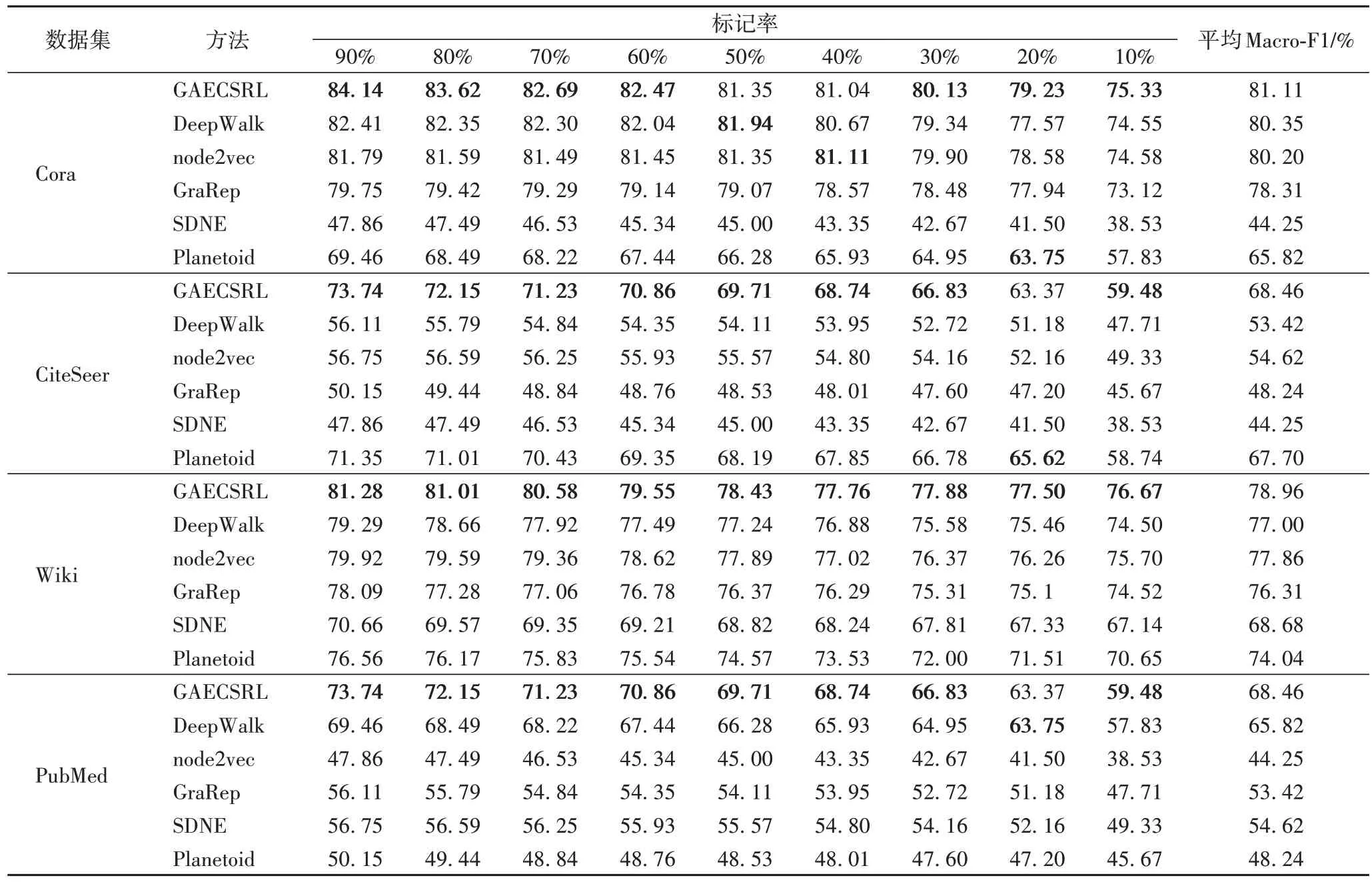
表4 不同数据集上节点分类的Macro-F1值 单位：%Tab.4 Macro-F1 values of node classification on different datasets unit：%

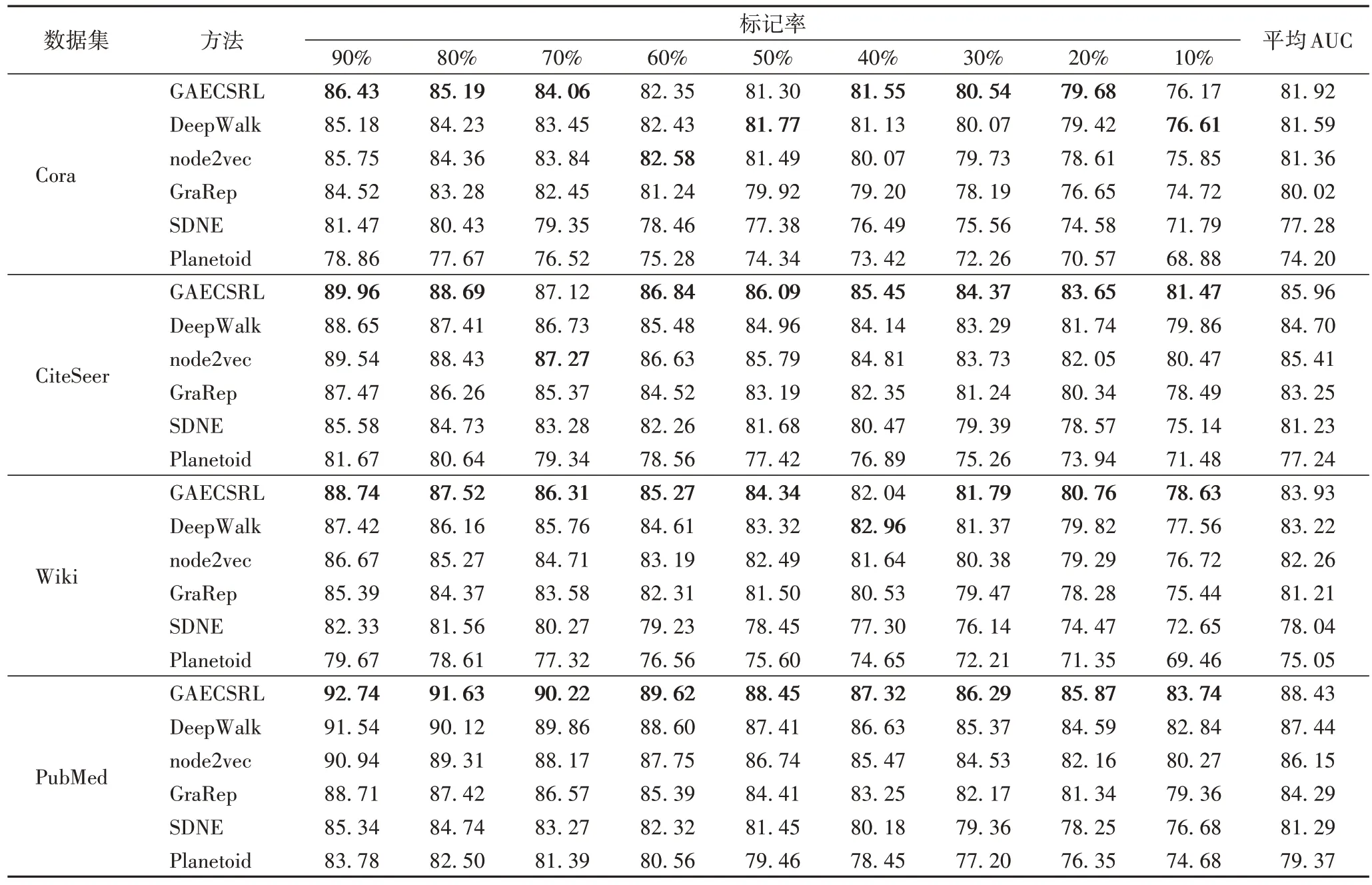
表5 不同数据集上链接预测的AUC值 单位：%Tab.5 AUC values of link prediction on different datasets unit：%

从表3～5 中可以看出，随着节点标记率的提高，GAECSRL 和基线方法在节点分类和链接预测中的评价指标有所提高，说明节点标签在生成网络表示的过程中起着重要作用，加入节点标签，使得GAECSRL 学习到的节点表示更具有代表性，与原始网络更接近。

表3 不同数据集上节点分类的Micro-F1值 单位：%Tab.3 Micro-F1 values of node classification on different datasets unit：%

表3 展示了在不同数据集上进行节点分类的Micro-F1值，在Cora 数据集上，GAECSRL 在标记率为50%和60%时Micro-F1 值仅次于DeepWalk，但是相差仅为0.36 和0.4 个百分点，其他情况优于基线方法；在CiteSeer 和Wiki 数据集上，GAECSRL 与基线方法相比最优；在PubMed 数据集上，标记率为20%时，GAECSRL 次于node2vec，仅比node2vec 低0.38个百分点。除此之外，GAECSRL 相较基线方法，在Cora 和Wiki 数据集上GAECSRL 提高了0.9～11.37 个百分点，在CiteSeer 和PubMed 数据集上提升了9.43～24.46 个百分点，效果较为明显，这是由于CiteSeer 和PubMed 为两个较大的数据集，且节点的标记率较高，使得GAECSRL 学习到的节点表示更优。

表4 展示了在不同数据集上进行节点分类的Macro-F1值，在Cora 数据集上，GAECSRL 在标记率为40%和50%时Macro-F1 值仅次于DeepWalk 和node2vec，相差分别为0.59和0.07 个百分点，其他情况优于基线方法；在CiteSeer 和Wiki 数据集上，GAECSRL 在标记率为20% 时，次于Planetoid，分别相差0.20 和2.25 个百分点；在PubMed 数据集上，GAECSRL 与基线方法相比最优。在Cora 和Wiki 数据集上，GAECSRL 相较基线方法提高了0.76～10.85 个百分点，在CiteSeer 和PubMed 数据集上提升了2.04～24.20 个百分点，效果较为明显，同样是由于CiteSeer 和PubMed 数据集较大、节点标记率高，获得了更优的网络表示。

表5 展示了在不同数据集上进行链接预测的AUC 值，在数据集Cora 上，GAECSRL 在标记率为50%和60%时，结果仅次于DeepWalk 和node2vec，相差0.47 和0.13 个百分点；在CiteSeer 数据集上，GAECSRL 在标记率为60% 时次于node2vec，相差0.15 个百分点；在Wiki 数据集上，GAECSRL在标记率为40%时，结果比DeepWalk 低0.92 个百分点，其他情况都是最优。在不同数据集上，与基线方法相比，GAECSRL 提升的百分点都在10 以内。

接下来研究了参数的敏感度，即参数α对节点分类性能的影响。实验中将节点分类训练比设置为50，α的取值范围为（0，1），在不同数据集上随着参数α变化，Micro-F1 和Macro-F1 值如图2 所示，可以看出Micro-F1 和Macro-F1 值受参数影响较小，参数敏感度低，所提GAECSRL 方法具有较好的鲁棒性，故在实验中设置α=0.5。

图2 不同数据集上α值对评价指标的影响Fig.2 Influence of α value on evaluation indexes on different datasets

4 结语

现实世界的网络数据具有丰富伴随信息，如标签信息和属性信息等，这些伴随信息对网络表示的生成有积极意义。所提方法将节点的标签信息、结构信息和属性信息加入网络表示学习的过程中，提出了一种结合图自编码器与聚类的半监督表示学习方法（GAECSRL）。该方法保持了网络的结构相似性和属性特征，用节点标签信息指导网络表示学习，提高了网络表示学习的可区分性。在真实数据集上进行节点分类和链接预测任务，与基准算法进行对比，实验证明了GAECSRL 方法的有效性。

GAECSRL 方法在实验过程中表现出了较好的性能，但是时间复杂度较高；此外，网络中仍存在其他高级的信息，如文本信息和语义信息等，而GAECSRL 只利用了节点的标签信息。今后的工作中，将考虑如何降低GAECSRL 的时间复杂度，同时将其他的高级信息融合到网络表示中。