基于自回归神经网络的多维时间序列分析

邱玉祥, 蔡 艳, 陈 霖, 万 明, 周 宇

(1. 南京南瑞信息通信科技有限公司, 南京 210003； 2. 南京航空航天大学 计算机科学与技术学院, 南京 211106)

时间序列是日常生活中常见的一类按时间顺序排列的数据, 其基本单元是由时间与数据构成的二元组. 目前， 数据挖掘领域对时间序列的研究较多, 包括时间序列相似性搜索、 子序列搜索、 降维、 分割、 可视化等[1]. 时间序列分析广泛应用于股市[2]、 天气[3]、 销售[4]、 异常检测[5]等领域. 本文对时间序列进行分析预测, 通过对历史序列所隐含的规律进行充分挖掘, 实现对未知序列的合理预测. 时间序列通常在每个时间点处包含多个相关特征, 称为多维时间序列. 各特征之间可能存在一定的相关性, 如何捕获并利用这些特征之间的依赖关系是多维时间序列分析的关键.

传统的基于自回归的预测方法包括Holt-Winters[6]和差分自回归移动平均模型(autoregressive integrated moving average model, ARIMA)[7]， 但这些方法只能捕获一维时间序列中的线性关系, 不能对多个特征及其之间的相关关系进行建模. 对于高维非线性的时间序列, 一些机器学习方法效果较好, 例如基于相似性搜索的k近邻(k-nearest neighbor,kNN)方法[8]、 基于结构风险最小化的支持向量机(support vector machine, SVM)算法[9]等.

近年来， 机器学习模型中的深度神经网络在相关领域得到广泛应用, 尤其在自然语言处理(natural language processing, NLP)领域和计算机视觉(computer vision, CV)领域产生了巨大影响. 例如能保存序列数据中隐含上下文信息的循环神经网络(recurrent neural network, RNN)[10]、 长短期记忆(long short-term memory, LSTM)网络[11]和门控循环单元(gate recurrent unit, GRU)[12]被用于对复杂序列数据进行建模. LSTM是对RNN的改进, 能捕获序列中的长期依赖, 缓解了RNN在训练过程中产生的梯度消失问题[13]. GRU能在提高训练效率的同时获得与LSTM相似的效果. 卷积神经网络(convolutional neural networks, CNN)[14]可有效从输入图像中按不同粒度提取局部和平移不变性特征. 目前, 深度神经网络已广泛应用于时间序列分析任务中[15-22], 即使用过去观察到的时间序列预测一段时间后未知的时间序列, 预测的时间点距离当前时间点越远, 预测难度越大. 因此, 神经网络更适合处理具有复杂周期性重复模式的多维时间序列.

差分自回归移动平均模型源于Box-Jenkins方法[16], 使用差分的方式构建平稳的时间序列, 通过偏自相关系数(partical autocorrelation coefficient, PAC)和自相关系数(autocorrelation coefficient, AC)检验数据的平稳性. ARIMA模型因其统计学特性和模型选择过程中的Box-Jenkins方法而得到广泛使用. 文献[17]用ARIMA模型和神经网络相结合的方式, 充分利用神经网络能处理非线性数据的特点将ARIMA模型预测获得的残差进行建模, 最后将二者的结果进行融合. 文献[18]用SVR和ARIMA的混合模型进行时间序列分析, 并在数据预处理部分使用了集成经验模态分解方法. 虽然ARIMA模型具有很多优势和变体, 但由于其较高的计算成本, 因此很少用于多维时间序列分析.

时间序列分析问题可视为带有时变参数的标准回归问题. 因此, 可将包含不同损失函数和正则化项的各种回归模型应用于时间序列分析任务. 例如, 向量自回归(vector autoreg ression, VAR)模型由AR模型扩展到多维得到, 由于其简单性在多维时间序列分析中应用广泛[19]； 线性岭回归(linear ridge regression, LRidge)是在传统线性回归损失函数的基础上添加了正则化项以防止过拟合. 由于机器学习社区具有高质量求解器, 因此这些线性方法在多维时间序列分析中更方便. 但这些线性模型可能也无法捕获多维数据的复杂非线性关系, 从而导致其性能低下. Flunkert等[20]提出了一种DeepAR技术, 通过假设时间序列的潜在分布进行概率预测. 利用多层感知机(multi-layer perception, MLPs)估计每个时间点的分布参数, 可得到目标变量的概率密度函数. 陈海鹏等[21]采用小波变换与极限学习机(extreme learning machine, ELM)相结合的方法， 对短时空剩余停车泊位进行了预测； 魏晓辉等[22]针对现有方法利用网络信息相对割裂难以描述链接次数与相似性分数关系的问题, 提出了一种动态网络中的链接预测方法, 用节点相似性分数和链接次数组合时间序列模型进行预测; Bahdanau等[23]提出了一种用编码器和解码器结构对原句子进行编码, 并在解码器阶段使用注意力(Attention)机制决定应该关注原句子的哪些部分产生目标单词; Qin等[24]通过在传统循环神经网络的输入和输出部分加入Attention机制, 提出了基于双阶段注意力机制的DA-RNN(dual-stage attention-based recurrent neural network)模型； Fan等[25]针对时间序列多步预测提出了一个端到端的深度学习框架, 结合Attention机制在每个未来时间步使用解码器的隐含状态关注到多个不同的历史周期.

1 框架设计

1.1 问题描述

本文考虑多维时间序列分析, 即每个时间点的数据是一个包含多个特征的向量， 表示每个时间点的数据含有多个维度的特征， 每个特征对应的时间序列位于不同的范围. 首先需对它们分别进行均值和方差归一化处理， 然后通过滑动窗口的方式批量采集数据, 形成〈输入,输出〉的数据对, 输入数据的格式为XT=(x1,x2,…,xT)∈n×T, 其中T表示滑动窗口的长度, 即一次预测需要回看多少个时间点的数据,xT表示当前时间点的特征向量,n表示特征向量的长度.输出数据用Y=yT+d∈表示, 其中d表示延迟步数, 即预测目标是当前时间点d个时间步后的数据.

本文实验采用单步预测评估模型效果, 即每次预测未来一个时间点的数据.实际中可设h=1, 并通过滚动预测的方式实现多步预测, 即每次用每个特征的预测值代替真实值, 形成新的窗口(x2,x3,…,xT+1)并预测得到yT+d+1的数据.多步预测不宜预测过长的时间点, 因为预测结果存在偏差, 使用预测数据取代真实数据会导致预测结果的偏差逐渐增大.一般情况下, 滑动窗口的长度T和延迟步数d由实际环境的要求设定.本文提出的自回归神经网络(autoregressive neural network, ARNN)整体结构如图1所示.该模型是专为含有动态相关关系和复杂周期性重复模式的多维时间序列设计的一个深度学习框架.

1.2 卷积部分

本文提出的自回归神经网络由卷积部分和循环部分组成, 输入同时传入到这两部分中.卷积部分结构如图2所示.卷积神经网络不包含池化层, 目的是提取时间维度的短期模式和特征维度的依赖关系[26].其使用多个长度为ω、 宽度为n(n为特征维度的大小)的卷积核, 操作如下： 第k个卷积核扫过输入矩阵X并产生

fk=RELU(Wk*X+bk),

(1)

其中*表示卷积操作,fk表示输出向量, RELU(x)=max{0,x}.首先通过在输入矩阵X的侧边进行零填充, 使每个输出向量fk长度为T.卷积操作的输出矩阵大小为dc×T, 其中dc表示卷积核的个数.然后通过展平和全连接操作将输出矩阵映射成一个固定长度的向量c， 该向量表示卷积部分提取的信息, 长度与循环部分的输出向量保持一致, 目的是平衡两部分对最后预测结果的影响[27].

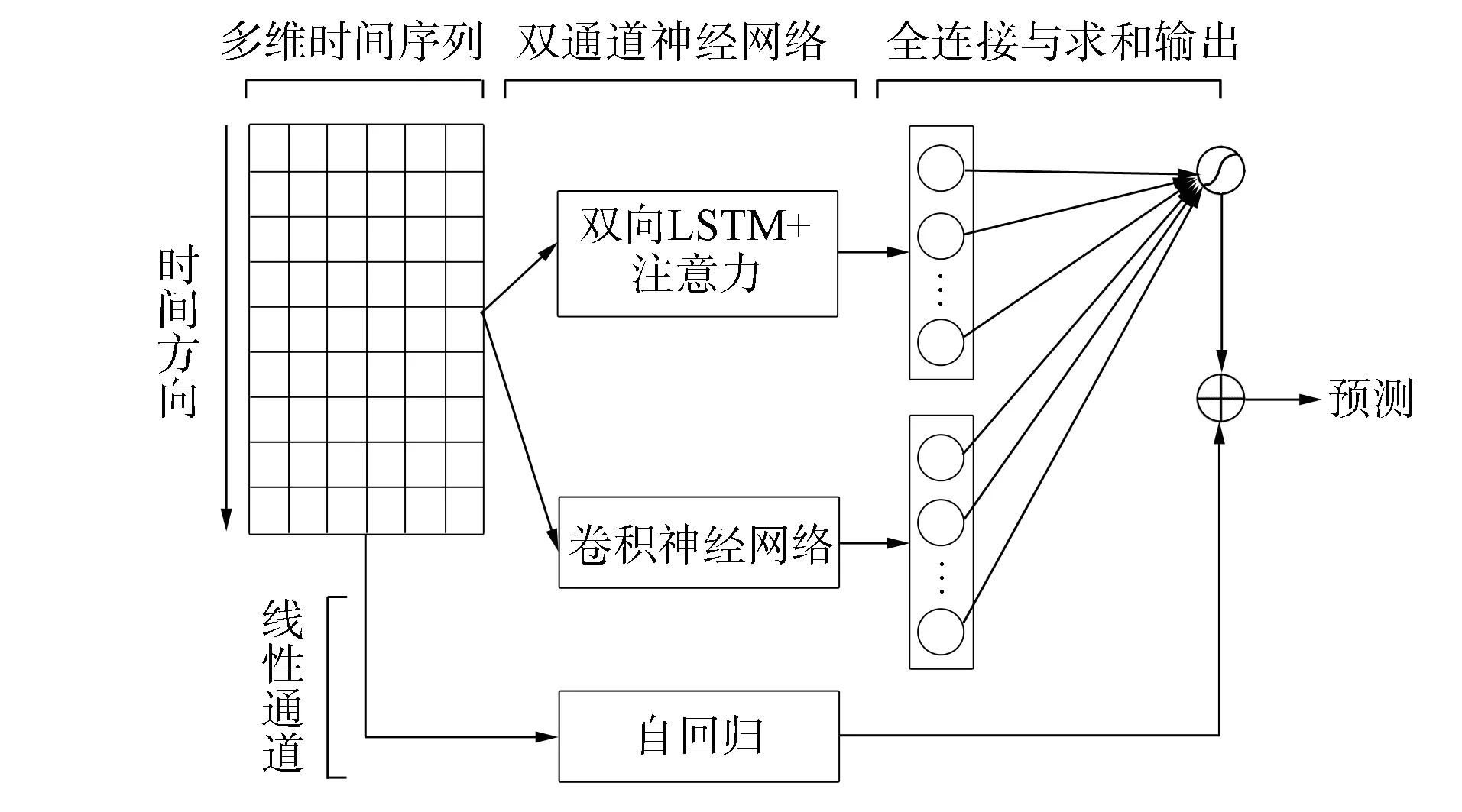
图1 模型结构Fig.1 Model structure

图2 卷积部分结构Fig.2 Convolutional component structure

1.3 循环部分

循环部分利用时间序列的顺序敏感性, 使用双向LSTM层捕获正序和逆序两个方向上的长期模式, 并将它们的结果合并. 双向LSTM能捕获可能被单向LSTM忽略的模式， 其结构如图3所示. 计算过程如下：

其中式(4)表示向量拼接操作. 每个方向的LSTM引入了一个新的跨越多个时间步的数据流, 具有跨越时间步的信息[28], 在时间t处循环单元的隐含状态计算公式为

其中xt和ht-1分别表示当前时刻的输入和上一时刻的隐含状态, 式(5)表示模型当前的输入值, 式(6)～(8)分别表示输入门、 遗忘门和输出门, 式(9)表示对状态的更新, 式(10)表示模型当前的输出值.

图3 循环部分结构Fig.3 Recurrent component structure

1.4 时间注意力层

双向LSTM的输出由两个方向上最后一个循环单元的隐含状态拼接得到. 由于双向LSTM在循环单元的计算中存在梯度消失等问题, 只取最后一个循环单元的隐含状态可能会存在信息丢失的情况.因此, 本文在循环部分的输出层引入注意力机制[23], 有选择性地关注每个循环单元的隐含状态.本文设计的时间注意力层可表示为

其中ht表示每个循环单元的隐含状态,αt表示每个ht对应的权重向量,HT=(h1,h2,…,hT)是由每个循环单元隐含状态堆叠形成的矩阵, score表示基于乘法的注意力分数计算方式， 式(11)和式(12)通过softmax归一化操作求得每个ht对应的权重后对其进行加权求和，r表示时间注意力层的输出, 即整个循环部分的输出向量.

使用全连接层组合神经网络中卷积部分和循环部分的输出.全连接层的输入包括卷积部分的输出向量c和循环部分的输出向量r.使用hD作为全连接层的输出, 即图1中神经网络在当前时间点处的预测结果, 形式化表示为

hD=Wrr+Wcc+b.

(14)

1.5 自回归层

由于卷积和循环神经网络很难捕捉数据的线性特征, 因此本文借鉴LSTNet[29]使用自回归(autoregression, AR)模型对丢失的线性信息进行特征提取. 将AR部分的预测结果表示为hL∈, 内部参数表示为Wa∈q×n和ba∈n, 其中q是输入矩阵上输入窗口的大小,n是输入数据特征维度的大小.AR模型形式化表示为

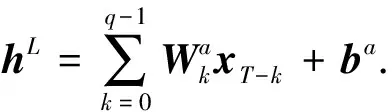
(15)

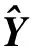
(16)

1.6 目标函数

在回归问题中常用的目标函数有绝对值损失(L1损失)和平方损失(L2损失).绝对值损失的优势在于其在含有异常值的时间序列中更能保证模型的鲁棒性[30]； 平方损失是许多预测任务默认的目标函数, 在优化过程中更稳定和准确.两个目标函数形式化表示为

(18)

其中Θ表示模型中的参数集合,Ωtrain是用于训练的数据集合, ‖·‖F是Frobenius范数. 具体使用哪个目标函数将在实验部分通过模型在验证集上的评估结果决定. 目标函数的优化策略可选用动量梯度下降(SGD)或其变体Adam[31].

2 实 验

为验证自回归神经网络的预测效果, 在两个不同领域的数据集上使用4种方法(包括本文方法)分别进行实验.

2.1 对比方法

本文使用如下方法进行对比实验：

1) AR表示自回归模型, 它等价于一维VAR模型, 多维时间序列通过展平操作可变为一维.

2) LRidge是添加了L2正则化项的向量自回归模型, 由于其简单性和高效性， 因此在多维时间序列分析中广泛使用.

3) DeepAR是基于自回归循环神经网络的概率预测模型, 通过综合结果得到预测值.

2.2 评价指标

模型使用均方根误差(RMSE)、 平均绝对值误差(MAE)和R2作为度量指标, 分别定义为

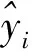
2.3 数据集

实验使用两个数据集.数据集valve(https://github.com/Caleb411/ARNN/tree/mian/data)是某电网内冷水系统各项指标的真实数据, 每0.5 h采集一次, 共29 056个时间点, 不包含缺失值. 该数据集包含4个维度的特征, 分别是进阀温度、 出阀温度、 进阀压力和冷却水电导率, 本文预测进阀温度.

另一个负荷数据集power(https://archive.ics.uci.edu/ml/machine-learning-databases/00235/)源于UCI数据库. 由于原始数据采集频率较高且含有缺失值, 因此首先要对该数据集按小时进行重采样并按各特征维度的均值进行缺失值填充. 最后得到包含34 587个时间点的数据集, 包含7个维度的特征, 分别是有功功率、 无功功率、 电压、 强度等, 本文预测有功功率.

本文实验采用数据集中所有的维度作为特征, 仅预测某一个指标. 两个数据集都根据6∶2∶2的比例按时间顺序划分为训练集、 验证集和测试集. 因为具有较低离散程度和平稳性的时间序列可预测性更强， 所以针对本文使用的两个数据集, 分别计算预测特征的方差， 并进行时间序列平稳性(ADF)检验. 方差使用无偏估计, 公式为

(22)

平稳性代表了某种程度上的时间平移不变性, 如果时间序列的性质随时间的偏移不发生明显变化, 则认为时间序列是平稳的. 若序列平稳, 则ADF存在单位根, 否则不存在单位根. ADF的原假设是数据存在单位根, 当检验值小于1%时则称显著拒绝原假设. 数据集预测指标方差和ADF值列于表1.

表1 数据集预测指标方差和ADF值

由表1可见, 两个数据集都是平稳的, 但数据集valve由于方差更小, 预测效果可能会更好. 两个数据集中需要预测的特征随时间的变化分别如图4和图5所示. 为检验其中存在的重复模式, 进一步绘制自相关函数图， 结果如图6和图7所示.

图4 数据集value进阀温度随时间的变化Fig.4 Inlet valve temperature of valve dataset changes with time

图5 数据集power有功功率随时间的变化Fig.5 Active power of power dataset changes with time

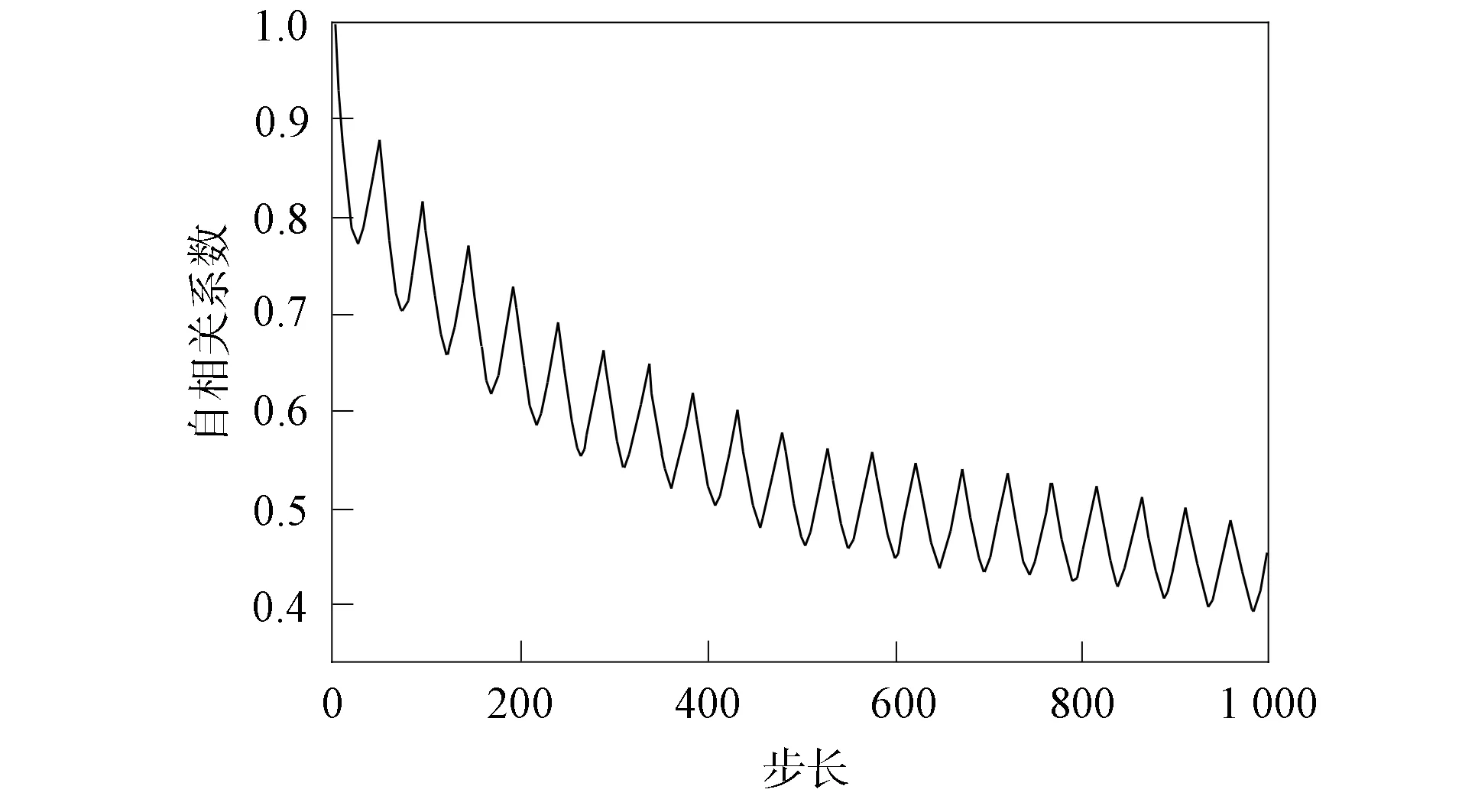
图6 数据集valve进阀温度自相关函数Fig.6 Autocorrelation function of inlet valve temperature of valve dataset

图7 数据集power有功功率自相关系数Fig.7 Autocorrelation coefficient of active power of power dataset

自相关函数, 也称为序列相关函数, 其反映了时间序列与其自身延迟副本之间的相关关系随延迟阶数τ的变化情况, 定义为

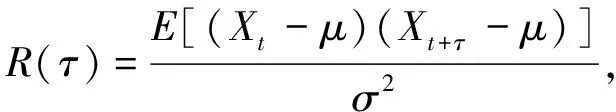
(23)

其中Xt表示某个时间点的数据,μ表示均值,σ2表示方差.实际应用中使用无偏估计量计算自相关系数.由图6和图7可见， 两个数据集均存在一定的周期性重复模式, 其中数据集power更明显.理论上， 如果数据中存在周期性重复模式, 则模型将取得较好的预测效果， 周期性重复模式越明显的数据集越能发挥本文模型的优势.

2.4 实验参数设置

实验中模型各部分的参数设置列于表2， 其中T表示滑动窗口的长度.在本文模型的卷积部分中, 参数filters表示卷积通道的数目, kernel_size表示卷积核的长度, output_size表示输出向量的长度,这里与循环部分保持一致. 对比模型DeepAR和本文模型循环部分中LSTM的隐含状态长度hidden_size均与filters保持一致, 输入数据批量的长度batch_size均设置为128. 对于其他可调整的超参数, 在两个数据集的验证集上分别进行调整获得最好的效果. 对比模型LRidge的正则化系数λ从{0.1,1,10}中选取. 本文模型中AR部分的输入窗口大小q从{3,6,12,24,48}中选取. 利用Adam[27]算法对模型的参数进行优化.

表2 超参数设置

2.5 实验结果

不同模型在两个数据集上的对比结果分别列于表3和表4. 这里将延迟步数d设置为3, 即在数据集valve中预测1.5 h后的数据, 在数据集power中预测3 h后的数据. 由表3和表4可见, 本文提出的自回归神经网络在两个数据集上的R2指标分别达到95.58%和31.63%, 在数据集valve上相比于基准模型分别约提升3%,2%和1%, 表明本文模型对于具有平稳性的时间序列能较好地捕获其中存在的重复模式.

表3 不同模型在数据集valve上的对比结果

表4 不同模型在数据集power上的对比结果

由两个数据集的对比结果可见, 数据集valve上的预测效果整体比数据集power好, 但数据集power相较于对比模型效果提升更明显. 在数据集power中本文模型相比于AR模型提升了91%, 相比于LRidge模型提升了75%, 因为AR和LRidge这两个传统模型只捕获到了时间序列中的线性关系, 未能捕获到其中存在的非线性关系. 与DeepAR模型相比, 本文模型在R2上高出12%. DeepAR模型仅考虑了时间方向上的依赖关系, 未涉及到多个输入特征之间的相关关系. 数据的方差越小, 离散程度越低, 模型的预测效果越好, 且对于周期性重复模式更明显的数据集, 本文模型的优势更明显.

2.6 消融实验

为验证本文框架设计的性能, 在自回归神经网络中去除某些组件, 进行消融实验. 首先, 将去除或替换某些组件后的模型命名如下.

1) ARNNw/oAR： ARNN模型去除AR部分;

2) ARNNw/oCNN： ARNN模型去除卷积部分;

3) ARNNw/oTA： ARNN模型中的循环部分去除时间注意力层, 取双向LSTM两个方向上最后一个时间点的输出向量合并作为循环部分的输出向量;

4) ARNN-GRU： ARNN模型中循环部分的LSTM替换成GRU.

对于不同的比较基准, 调整模型的隐含维度使其与完整的自回归神经网络ARNN有相似的参数量, 以去除由模型复杂度导致的性能增益.

测试结果使用RMSE，MAE和R2三个指标进行评价, 结果分别列于表5和表6. 由表5和表6可见, 本文模型在两个数据集上都获得了最好的效果. AR部分作为自回归神经网络的线性部分关注时间序列的局部尺度变化, 对整体模型的性能有提升作用. 去除神经网络的卷积部分后, 在两个数据集上模型性能均有下降, 表明卷积部分在提取序列数据中的局部信息方面具有重要作用. 去除时间注意力层后在数据集power上出现了性能较大的下降, 表明有选择性地关注每个时间点的输出信息比只关注最后一个时间点的输出更有效. LSTM使用GRU替换后性能有所下降, 表明使用计算量更少的GRU在获得更快训练速度的同时, 也可能存在欠拟合的情况.

表5 不同模型在数据集valve上消融实验的对比结果

表6 不同模型在数据集power上消融实验的对比结果

为直观观察本文模型对于时间序列线性和非线性部分的捕获能力, 即对于数据尺度变化的鲁棒性, 将去除AR部分的ARNNw/oAR和本文模型ARNN的预测效果进行对比. 在数据集valve测试集上选取尺度变化较大的250个连续时间点, 预测结果分别如图8和图9所示， 其中实线表示真实数据, 虚线表示模型的预测结果.

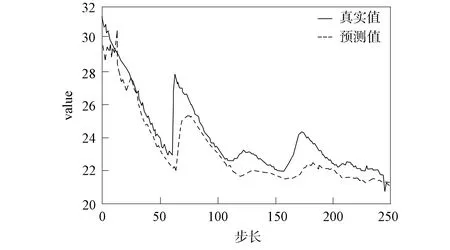
图8 ARNNw/oAR预测效果Fig.8 Prediction effects of ARNNw/oAR

图9 ARNN预测效果Fig.9 Prediction effects of ARNN

由图8和图9可见, 本文模型ARNN在峰值附近的预测效果好于ARNNw/oAR, 对时间序列随时间的尺度变化更敏感. 该消融实验证实了本文模型架构设计的效率. 所有部分对于整体模型的高效性和稳定性均有贡献.

综上所述, 针对多维时间序列分析传统方法多数需要依靠手动建立时间依赖关系探索历史数据中隐含规律的问题, 本文提出了一种新的基于自回归神经网络的方法进行多维时间序列分析. 通过结合卷积、 循环神经网络和自回归层, 在两个不同领域的数据集上与多个经典模型对比并获得了较优性能. 本文方法卷积部分能捕获多维输入变量间的局部模式, 循环部分能保持序列中两个方向的长期依赖信息, 自回归层专门针对线性关系进行特征提取. 同时, 在循环部分加入了能关注到每个时间点输出结果的时间注意力机制. 在数据探索阶段通过绘制自相关函数图, 用求方差和单位根的方式对数据的平稳性和周期性进行检验. 实验结果表明， 本文模型成功捕获了数据中存在的重复模式, 并通过结合线性和非线性模型提升了模型的鲁棒性.