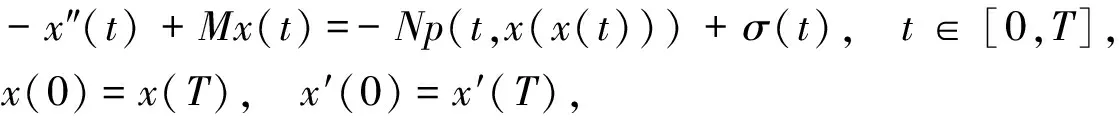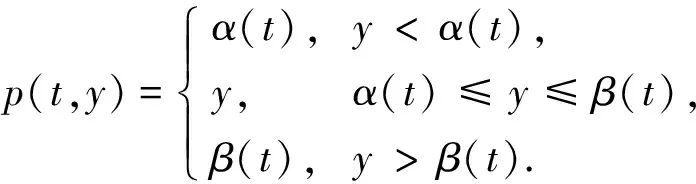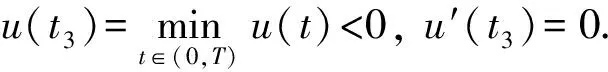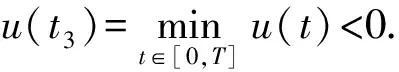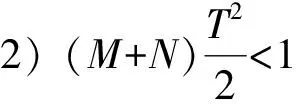一类二阶迭代微分方程周期问题解的存在性
2022-09-24康慧君
康 慧 君
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
迭代微分方程是一类泛函微分方程, 有很强的实际应用背景, 目前已得到广泛关注[1-16]. 例如: 古典的Euler几何问题可导出方程
x(t)x′(t)=x(c+x(t));
Poisson几何问题可导出方程
x(x(t))+x(x(t))x′(x′(t))-x(x(t+x(t)x′(t)))=1.
Cooke[1]提出了生物学中的重要方程
x′(t)+ax(t-h(t,x(t)))=F(t),
该方程与遗传现象有关. 此外, 迭代微分方程在人口模型[2]、 日用品的价格波动模型[3]和血细胞的生产模型[4]中均有重要应用. 特别地, Eder[5]用压缩映射原理讨论了一阶迭代微分方程
x′(t)=x(x(t)),x(t0)=t0,t0∈[-1,1]
x′(t)=f(x(x(t))),x(0)=0
局部解的存在性. Kaufmann[7]用Schauder不动点定理研究了二阶迭代微分方程
x″(t)=f(t,x(t),x(x(t)),t∈[a,b]
(1)
在满足如下边界条件之一下解的存在唯一性:
x(a)=a,x(b)=b;
(2)
x(a)=b,x(b)=a.
(3)
其中f: [a,b]××→是连续函数.
设f满足如下条件:
(H1) 存在常数K,L>0, 使得

(H2) 存在M,N>0, 使得
|f(t,u1,v1)-f(t,u2,v2)|≤M|u1-u2|+N|v1-v2|,t∈[a,b],u1,u2,v1,v2∈.
文献[7]得到如下结果:
定理1[7]若f满足条件(H1), 则问题(1)-(2)或问题(1)-(3)存在解, 若f满足条件(H2), 则问题(1)-(2)或问题(1)-(3)存在唯一解.
上述结论是在f有界情形下考虑解的存在唯一性, 本文考虑当f无界时, 二阶迭代微分方程周期边值问题是否也可建立解的存在唯一性结果, 即考虑一类二阶迭代微分方程周期边值问题
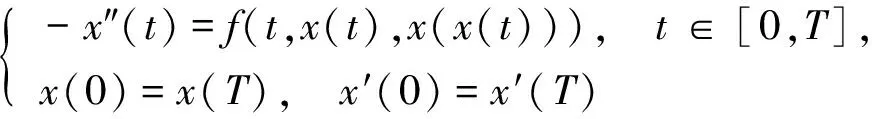
(4)
解的存在性.
本文总假设:
(H3)f: [0,T]×2→是连续函数.
1 引 理
下面用极大值原理说明单调迭代方法的正确性.
引理1设x∈E=C([0,T],)∩C2([0,T],), 若存在M>0,N>0, 使得下列条件成立:
1) -x″(t)+Mx(t)+Nx(x(t))≥0,t∈[0,T];
2)x(0)=x(T),x′(0)≤x′(T);
则∀t∈[0,T],x(t)≥0.
证明: 反设x(t)<0,t∈[0,T].考虑如下两种情形.
情形1) 设x(t)≤0,x(t)不恒为0,t∈[0,T].在该情形下, 可得x(0)=x(T),x′(0)≤x′(T),x″(t)≤0,t∈[0,T], 因此在区间[0,T]上x(t)=K<0, 其中K是常数.从而
0≤-x″(t)+Mx(t)+Nx(x(t))=(M+N)K,
与K<0矛盾.
情形2) 存在t1,t2∈[0,T], 使得x(t1)>0,x(t2)<0.此时, 又有如下两种情形.
①x(0)=x(T)>0.此时, 存在t3∈(0,T), 使得
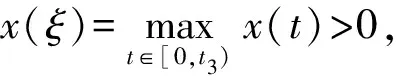
x″(t)≤(M+N)x(ξ),t∈[0,t3).
(5)
对式(5)两边从s(ξ -x′(s)≤(t3-s)(M+N)x(ξ), (6) x″(t)≤(M+N)x(ξ),t∈[0,T]. (7) 当ξ>t3时, 对式(7)两边从t3(t3 x′(s)≤(s-t3)(M+N)x(ξ), (8) 引理2设x∈E=C([0,T],)∩C2([0,T],), 若存在M>0,N>0, 使得下列条件成立: 1) -x″(t)+Mx(t)+Nx(x(t))≥0,t∈[0,T]; 2)x(0)=x(T),x′(0)≤x′(T); 则∀t∈[0,T],x(t)≥0. 证明: 反设x(t)<0,t∈[0,T].考虑如下两种情形. 情形1) 设x(t)≤0,x(t)不恒为0,t∈[0,T].证明如引理1中情形1)的证明, 故略. 情形2) 存在t1,t2∈[0,T], 使得x(t1)>0,x(t2)<0.此时, 又有如下两种情形. ①x(0)=x(T)>0.此时, 存在t3∈(0,T), 使得 -x″(t)+Mx(t)≥-Nx(ξ),t∈[0,t3). x′(t)=emt(v′(t)+mv(t)),x″(t)=emt(v″(t)+2mv′(t)+m2v(t)). 因此-v″(t)-2mv′(t)≥-Ne-mtx(ξ),t∈[0,t3), 即 (e2mtv′(t))′≤Nemtx(ξ),t∈[0,t3). (9) 对式(9)两边从s(ξ v′(t3)=e-mt3x′(t3)-mv(t3)=-mv(t3)>0, 可得 即 (10) 对式(10)两边从ξ到t3积分, 得 即 而 从而 与条件3)矛盾. ②x(0)=x(T)≤0.此时, 存在t3∈[0,T], 使得 -x″(t)+Mx(t)≥Nx(ξ),t∈[0,T]. 当ξ (e2mtv′(t))′≤Nemtx(ξ),t∈[0,T]. (11) 对式(11)两边从t3(t3 即 (12) 对式(12)两边从t3到ξ积分, 得 即 而 从而 与条件3)矛盾.证毕. 为在问题(4)中利用单调迭代方法, 考虑如下线性周期边值问题: (13) 其中σ∈C([0,T],). 若存在α∈E满足 则α称为问题(13)的一个下解; 反之, 若存在β∈E满足 则β称为问题(13)的一个上解. 对于α,β∈E, 如果α(t)≤β(t),t∈[0,T], 则有如下表示: [α,β]={x∈E:α≤x≤β}. 定理2假设问题(13)存在一个下解α和一个上解β, 满足α≤β, 且引理1中条件3)成立, 则问题(13)有唯一解x∈[α,β]. 证明: 考虑周期边值问题 (14) 其中 易验证p: [0,T]×→是连续的. 定义算子Φ:E→E为 (15) 其中 m=M1/2.则算子Φ:E→E是全连续算子. 由于-Np(t,x(x(t)))+σ(t)在[0,T]上有界, 则Φ在E上也有界.根据Schauder不动点定理知, 存在算子Φ的一个不动点x, 使得x∈E是问题(14)的一个解. 下面证明x∈[α,β].首先证明x≥α.设u(t)=x(t)-α(t).由于p(t,x(x(t)))-α(x(t))≤max{u(x(t)),0},t∈[0,T], 则由下解的定义可得: (i) -u″(t)+Mu(t)+Nmax{u(x(t)),0}≥0,t∈[0,T]; (ii)x(0)=x(T),x′(0)≤x′(T); 反设x(t)<α(t),t∈[0,T].考虑如下两种情形. 情形1) 设u(t)≤0,u(t)不恒为0,t∈[0,T].此时可得u(0)=u(T),u(0)′≤u′(T),u″(t)≤0,t∈[0,T], 因此在区间[0,T]上u(t)=K<0, 其中K是常数.从而 0≤-u″(t)+Mu(t)+Nmax{u(x(t)),0}=MK, 与K<0矛盾. 情形2) 存在t1,t2∈[0,T], 使得u(t1)>0,u(t2)<0.此时, 又有如下两种情形. u″(t)≤(M+N)u(ξ),t∈[0,t3). u″(t)≤(M+N)u(ξ),t∈[0,T]. 若存在α∈E满足 则α称为问题(4)的一个下解; 反之, 若存在β∈E满足 则β称为问题(4)的一个上解. 定理3假设存在问题(4)的一个上解α和一个下解β, 使得在[0,T]上α≤β.并存在常数M>0,N>0, 满足下列条件: 1)f(t,u2,v2)-f(t,u1,v1)≥-M(u2-u1)-N(v2-v1),t∈[0,T],α(t)≤u1≤u2≤β(t),α(x(t))≤v1≤v2≤β(x(t)); 则存在序列{αn}非减、 {βn}非增, 使得其在[α,β]上单调一致收敛于问题(4)的极值解, 其中α0=α,β0=β. 证明: 对于η∈[α,β], 考虑如下问题: σ(t)=ση(t)=f(t,η(t),η(x(t)))+Mη(t)+Nη(x(t)). (16) 由于η∈[α,β], 由条件1)和上下解的定义知 -β″(t)+Mβ(t)+Nβ(x(t))≥ση(t). 因此,α和β分别是问题(16)的一个上解和下解.根据定理2, 定义算子A: [α,β]→[α,β],Aη是问题(16)的唯一解.由引理1可知A是[α,β]上的单调增算子, 即η1,η2∈[α,β],η1≤η2,Aη1≤Aη2. 定义序列{αn},{βn}, 其中αn+1=Aαn,βn+1=Aβn,α0=α,β0=β.则有 α0=α≤α1≤…≤αn≤βn≤…≤β0=β. 在[0,T]上单调一致有界, 从而α*(t),β*(t)是问题(4)的解. 进一步, 若x∈[α,β]是问题式(4)的解, 则由归纳法可知,αn(t)≤x(t)≤βn(t),t∈[0,T],n=0,1,2,…, 因此x∈[α*,β*].于是α*(t),β*(t)分别是问题(4)在[α,β]上的极小值解和极大值解.证毕.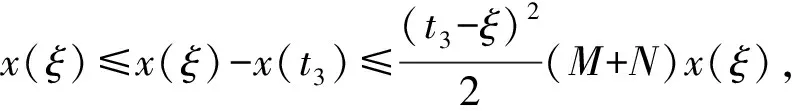
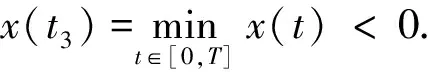
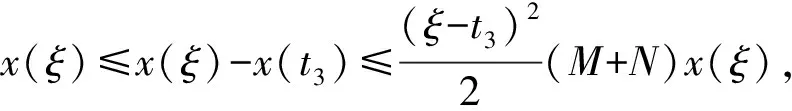
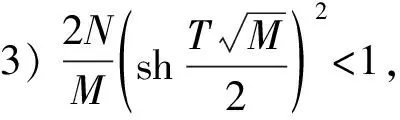
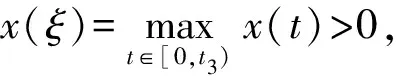
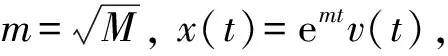
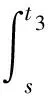
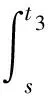
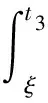
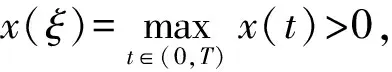
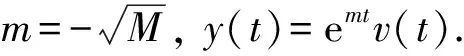


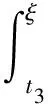
2 主要结果