基于累积前景理论的通勤者换乘出行决策研究

陈亮，刘晟宇，田蓓，李巧茹

(河北工业大学 土木与交通学院，天津 300401)

通勤出行作为我国城市公共交通的重要组成部分，对于北京、上海和天津等超大型城市来讲，由于高峰期出行拥堵，居民采用公共交通通勤的比例较高，且随着城市区域面积的拓增与公交系统的不断完善，换乘出行方式在居民通勤中占有比重逐渐升高。高峰期通勤者会根据预留出行时间和换乘等待时间做出换乘决策，二者已经成为影响通勤者换乘决策的重要因素。通勤出行作为一种居民日常出行行为，一直以来都是交通领域研究的重点，研究结论对于预测城市高峰期通勤者的换乘决策、提升通勤者的出行满意度具有重要意义。部分学者曾针对居民出行过程中的换乘行为做出研究。在轨道交通换乘方面，池丹等[1]将出行费用与出行时间引入效用函数固定项中，从而构建广义出行费用的轨道交通换乘方式选择模型。梁春岩等[2]在实际调查数据的基础上，利用多元Logistic模型分析了相关因素对城市居民选择轨道交通换乘方式的影响程度。李艺等[3]通过对比分析实际出行与模型的换乘客流行为特征，提出了绕行换乘的概念。在其他交通方式换乘方面，SHRIVASTAVA等[4]通过建立数学模型，优化了出行者的换乘时间成本。王京元等[5]运用Anylogic仿真软件，针对出行者的高铁换乘城市轨道交通的过程进行了研究。马书红等[6]提出了一种基于出行链的混合选择模型，分析了城际旅客换乘选择行为。四兵锋等[7]研究了换乘时间与换乘距离对路径选择的影响。钱堃等[8-9]通过分析乘客因拥挤延误无法上车的情况，提出了拥挤延误阻抗函数。以上学者探究了不同场景下出行者换乘决策的影响因素，但并没有结合通勤者的心理探究不同出行情景下预留出行时间与换乘等待时间对换乘决策产生的影响。1979年，KAHNENMAN等[10]基于人们的有限理性提出前景理论，并在1992年进一步完善了理论模型，发展成为累积前景理论[11]，相较于传统研究理论，其能够更加准确地描述个体在不确定情况下的决策行为。胡晓伟等[12]将出行者按照收入水平进行分类，运用前景理论探究了不同收入的出行者在不同出行情景下的出行方式决策行为。张薇等[13]综合考虑出行时间与出行费用2项指标，探究了通勤者的最优出行方式，并基于不同参考点下通勤者的综合前景值变化，分析了参考点对出行决策的影响。黄兴建等[14]在基于前景理论的路径选择中，综合考虑出行时间成本与出行舒适度2个维度，通过和仅考虑出行时间成本的单维度模型进行比较，发现双维度模型更符合实际情况下通勤者的出行决策行为，并以通勤者出行过程中的期望费用及期望舒适度作为出行参考点。田丽君等[15]则把期望通勤费用及期望通勤时间组合成的期望出行总成本作为出行的参考点。INDRIANY等[16]通过对通勤者的出行时间进行调查，将参考点定义为通勤者可接受的平均出行时间。MANLEY等[17]研究了出行者决策的认知、记忆力和偏好等因素对路径选择的影响。AN等[18]运用累积前景理论对小汽车出行者在拥挤收费政策下的方式选择进行了探讨。王惠队等[19]运用累积前景理论对重大公共卫生事件影响下重点人群的出行行为进行了研究。综上所述，现有运用累积前景理论分析通勤者个体出行决策的研究主要集中于出行路径选择和出行方式选择，且主要考虑出行时间与出行费用，并没有将累积前景理论运用到换乘决策中。基于此，本文引入累积前景理论，建立高峰期通勤者面对不确定预留出行时间与换乘等待时间的换乘决策模型，为预测高峰期通勤者的换乘决策提供依据。

1 模型构建

基于累积前景理论的出行决策分为2个部分，即编辑阶段和评价阶段。编辑阶段指决策者首先设定自己的参考点，然后将不同决策所产生的结果编辑为相对于参考点的收益值或损失值；评价阶段指决策者根据价值函数对编辑阶段所产生的收益值与损失值进行计算，并根据决策权重函数做出主观概率评价。出行决策遵循效用最大化原则，前景值最大的决策即为最优决策。模型中各式所使用的变量及描述如表1所示。

表1 参数定义表Tab le 1 Parameter definition table

1.1 基本假设

由“2021城市交通出行问卷调查”结果显示，有29.1%的通勤者选择以常规公交及地铁为主的公共交通出行。根据魏华[20]的研究内容显示，国外大型城市公共交通出行比重在40%～80%之间。通过调查，在超、特大型城市中通勤者需通过一次换乘的方式到达工作地点的现象普遍存在。因此，本文提出S1和S22种换乘出行决策方案并进行研究，为高峰期通勤者的换乘决策提供依据。基于此，做出如下假设：

1)通勤者有2种换乘出行决策方案：S1和S2；

2)以常规公交为起泊车。

1.2 参考点的选取和价值函数的确定

参考点选取是累积前景理论研究中的核心内容，涉及价值函数的计算，同时通勤者会以参考点衡量出行过程中所感受的收益或损失。

本文选取到达时刻作为参考点[21]，到达时刻可以分为tE(收益临界)和tL(损失临界)2个参考点。利用2个参考点将整个时间段分为3个区间，(-∞,tE]和[tL,+∞)称为损失时段；(tE,)tL称为收益时段。由图1得出，价值函数曲线存在一个收益最大的峰值点，即为最偏好到达时刻，用tp表示。

图1 双参考点价值函数曲线Fig.1 Consider the value function of two reference points

在出行过程中，通勤者总是希望能够在接近tp的时间点到达。但在实际中并不能确保tij处于某个固定时间点，而是分布于(-∞,+∞)整个时间区间内。当时收益为时损失为V-(T)，且当tij=tp时收益值达到最大。

本文将tp设为伪参考点，结合tE和tL将价值函数曲线分为4个区域，得到基于累积前景理论的价值函数，如式(1)所示：

1.3 概率权重函数

本文采用文献[7]所提出的概率权重函数。

1)当tij∊(tE,)tL时，概率权重的计算公式如式(2)：

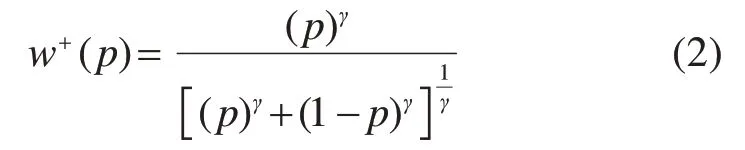
1.4 累积出行前景值V(T)

在本文建立的累积前景理论模型中，通勤者设定2种换乘出行方式{S1,}S2，并以tE和tL作为参考点分析{S1,}S2的出行前景值V(T)。X表示2种换乘选择的结果集，即通勤者在2种换乘方案下的收益或损失，xi∊X。通过参考文献[11]可以得到出行前景值与决策权重函数的公式。

出行前景值V(T)可表示为式(4)～式(6)：

决策权重函数可以表示为式(7)～式(11)：

通勤者在出行中面对不确定的预留出行时间Ty与换乘等待时间T时，主观估计2种决策的出行前景值V(T)，并选择V(T)较大的换乘方式出行。

2 算例分析

针对构建的理论模型进行算例分析，通过计算得出在不同Ty下的最优换乘决策方案。

2.1 决策情景描述与参数设置

S1和S2这2种换乘方式示意如图2，其行程时间概率分布见表2。假设通勤者具有同质性，参考文献[21]对通勤者出行时间约束的研究及夏金娇等[22]对通勤者要求到达时间的调查，本研究进行如下设定：

图2 通勤者出行路线示意图Fig.2 Schematic diagram of commuter travel routes

表2 2种换乘方式的行程时间分布Table 2 Travel time distribution of the two transfermethods

设定1：tp=tL-8min；

设定2：tE=tL-16m in；

设定3：20m in≤Ty≤90m in；

设定4：0m in≤T≤20m in。

其中设定1和设定2用于后文算例分析中tij位于收益时段或损失时段的判定；设定3和设定4对通勤者预留出行时间Ty与换乘等待时间T进行了约束，用于后文算例分析中计算tij的具体数值，从而得到不同时间约束下2种换乘方式的出行前景值。根据研究显示，设定3和设定4的时间约束符合大多数通勤者实际情况。

模型中，λ，η，γ和δ4个参数的取值对计算的结果至关重要。其中，λ(λ>1)表示通勤者对损失的厌恶程度，随λ取值增长，通勤者规避损失的意愿相应增加；η的取值同通勤者收益与损失风险的敏感性相关，η的取值越高，通勤者对损失风险越为敏感；γ和δ为计算概率权重函数的参数，其取值决定概率权重函数的凹凸程度，与概率权重呈非线性相关关系。本文中参数设置参考文献[10]的研究结果，具体如表3所示。

表3 模型参数设置Table 3 Modelparameter settings

2.2 通勤出行换乘决策分析

1)利用MATLAB对通勤者出行前景值V(T)进行分析，V(T)随Ty与T变化，如图3和图4所示。

图3 S1出行前景值Fig.3 S1 travelprospectvalue

图4 S2出行前景值Fig.4 S2 travelprospectvalue

由图可知，S1和S2方式出行前景值V(T)均随换乘等待时间Ty取值的增加呈现先上升后下降的趋势，这与现实出行场景中的通勤者获得的收益变化相符合，且Ty的取值过大或过小对通勤者均会产生损失。

2)为了更加细致分析不同换乘等待时间下S1和S2的出行前景值随Ty的变化趋势，取T分别为0，5，10，15和20m in，将S1和S2的V(T)进行对比，计算结果如表4所示。

当T=0，10和20 m in时，不同Ty取值对应的V(T)如图5所示。

图5 T=5,10,15,20m in时不同Ty取值下各决策的出行前景值V(T)对比图Fig.5 Comparison chartof the travel prospectvalue V(T)of each decision underdifferent Ty at T=5,10,15,20m inutes

综合分析图5与表4，以T=10为例，Ty取值为[20,60]m in时，S1的出行前景值V(T)小于S2的出行前景值V(T)，并且在Ty=45 m in时2种方式的V(T)相差最大为11.24，所以选择S2换乘出行方式；Ty取值为(60,90]m in时，S1的V(T)大于S2的V(T)，并且在Ty=85m in时2种方式的V(T)相差最大为11.53，所以选择S1换乘出行方式。

表4 出行前景值V(T)计算结果Table 4 Specific value of travelprospectvalue V(T)

同一种换乘方式，在Ty取值相同的情况下，随着T的增加，V(T)的变化比较明显。

综上所述，当Ty取值较小时，通勤者通常将面临迟到损失，在面对确定损失的情况下，为降低损失的程度，通勤者会选择在车时间大概率较短的S2换乘方式；当Ty取值较大时，通勤者通常面临早到损失，为规避损失获得收益，从而选择在车时间大概率较长的S1换乘方式。

3 结论

1)基于累积前景理论建立了通勤者换乘决策行为模型，综合考虑预留出行时间、换乘等待时间、在车出行时间、可接受最早到达时刻和工作开始时间等因素，定量分析了不同换乘等待时间下通勤者基于自身预留出行时间的最优换乘方式选择。

2)在到达时刻约束条件下，通勤者选择换乘方式的出行前景值与预留出行时间和换乘等待时间相关，通过分析得出预留出行时间过多或者过少，出行前景值均会减少。在预留出行时间较少时，换乘等待时间越长，通勤者越倾向于选择S2换乘方式出行。

3)所建立的模型不仅适用于常规换乘方式，同时还可以描述其他交通工具相结合的换乘方式，研究结果可以为城市高峰期通勤者的换乘决策提供依据，以提升通勤者的出行满意度。