大断面矩形顶管隧道开挖面稳定性三维极限分析方法
2022-09-23丁家浩彭立敏雷明锋朱立成唐志辉
丁家浩,彭立敏,雷明锋,2,朱立成,唐志辉
(1.中南大学 土木工程学院,湖南 长沙 410075;2.重载铁路工程结构教育部重点实验室,湖南 长沙 410075;3.中铁第六勘察设计院集团有限公司,天津 300308)
近年来,随着城市建设的快速发展,对城市地下空间建设的需求和要求也在不断提高。为了保证城市地面交通顺畅,在尽量避免“大开挖”的理念下,传统地下管道和人行通道施工技术越来越无法满足工程建设的需求,取而代之的是飞速发展的非开挖技术,其中就包括顶管技术。顶管法是一种类似于盾构法的地下工程非开挖管道铺设技术,具有综合成本低、施工周期短、环境影响小、不影响交通和施工安全性高等优势,已被广泛应用于地下人行通道、地下综合管廊等工程施工中[1]。相对于早期的以小断面、圆形截面为主的顶管隧道工程,近年新建的顶管隧道,断面尺寸越来越大,且为提高空间利用率,断面形式多设计为矩形结构。如2014年建成的郑州市红专路下穿中州大道隧道工程(高×跨=7.25m×10.1m),2017年建成的江苏苏州城北路综合管廊元和塘顶管工程(高×跨=5.5m×9.5m)均为大断面矩形结构型式[2]。毋庸置疑,这也必定会为顶管隧道的建造理论和施工安全带来新的挑战,其主要技术难点体现在大断面矩形顶管隧道的开挖面稳定性分析方法等方面[3]。目前,关于顶管隧道开挖面稳定性分析方法的研究,大多借鉴圆形盾构隧道领域的研究成果。BROMS等[4]建立基于极限平衡法的隧道开挖面稳定性筒仓分析理论;DAVIS等[5]提出顶进过程开挖面稳定系数塑性极限分析上限法等。此后,诸多学者在这些理论或模型的基础上,陆续针对顶管隧道开挖面稳定性影响因素、失稳破坏模式等方面开展了拓展性研究[6-7]。黄俊等[8]对隧道开挖面稳定性的影响因素进行详细分析,建立了开挖面稳定系数关于施工参数的函数;陈峥等[9]假定开挖面前方土体滑动面为对数螺旋线,继而推导得到了开挖面安全系数的目标函数;魏纲等[10]将传统三角形楔形体模型改进为由梯形楔体和上部的梯形棱柱组成的复杂截柱体模型,推导了开挖面最小支护压力计算方法,并开展了离心模型试验验证;MOLLON等[11-12]基于传统楔形体模型优化提出了隧道开挖面失稳的多锥体破裂体模式;SUBRIN等[13]构建了开挖面失稳的“牛角状”三维破裂体形态;雷明锋等[14]通过引入线路坡度角,建立了盾构隧道迎坡施工条件下开挖面极限支护力的计算模型。总之,上述成果的取得对顶管隧道的技术发展和推广应用起到了积极的促进作用。但纵观上述研究成果大多是基于圆形截面开展的。受开挖扰动机制与断面形式差异的影响,既有成果多难以直接适用于矩形断面隧道。特别是,对于大断面矩形顶管隧道开挖面稳定性分析与控制方法方面,现有理论还远远落后于工程实践,极有必要针对大断面矩形顶管隧道开挖面稳定性分析方法开展深入系统的研究。
1 矩形顶管隧道开挖面三维失稳模式
SUBRIN等[13]针对浅埋圆形盾构隧道开挖面失稳问题开展了细致的研究工作,提出了圆形盾构隧道开挖面前方失稳破坏的潜在破裂体为一绕隧道上方某点发生旋转而形成的类似于“牛角状”圆滑的三维滑动面,并开展了对比分析,验证了该模型的合理性。参考该方法,结合矩形顶管隧道的几何特征,可构建出矩形顶管隧道开挖面主动失稳破裂体形态,如图1。
基于图1所示的三维破坏机构,并假定破裂面满足相关联流动法则,则速度间断面上土体的应变率满足材料的Mohr-Coulomb准则[15-17]。于是,可建立如图2所示的矩形顶管隧道开挖面失稳破坏模型。图中,以A点为原点建立空间直角坐标系,A点和B点分别为矩形断面的上下顶点;E点为矩形断面的形心;C为隧道埋深;H为隧道高度;L为隧道宽度。

图1 矩形顶管隧道三维破坏机构Fig.1 Three-dimensional failuremechanism of rectangular pipe jacking tunnel

图2 矩形顶管隧道破坏模式示意图Fig.2 Schematic diagram of failuremode of rectangular pipe jacking tunnel
AF和BF上下2条曲线为开挖面破坏机构在YAZ平面的投影边界,其形状可以假设为以O点为中心的2条对数螺旋线,在坍塌破坏情况下,2条对数螺旋线相交于F点,并形成夹角为2φ,该点也为破坏体的顶点。由此,以O点为原点建立极坐标系,AF和BF上下2条曲线可用对数螺旋线方程表示[15]:

式中:θA,θB为描述破坏机构的角度参数;rA,rB分别是2条对数螺旋线的极径;φ为土体内摩擦角。
于是,可得到开挖面前方破裂体由被速度间断面分隔的刚性体组成,进而可构造空间旋转速度场以描述破坏土体的运动状态。即破坏土体以角速度ω绕过O点的X轴旋转,速度方向指向开挖面。当角速度确定时,破坏区内各点的速度大小仅与旋转半径r有关,而旋转半径r取决于O点的位置,因此不断优化O点的位置,便可计算出开挖面支护力极限值。
2 矩形顶管隧道开挖面破坏机构的空间离散
2.1 开挖轮廓空间离散
首先将矩形开挖面的轮廓离散,然后以轮廓离散点作为起始点生成速度间断面上的一系列点,进而构建出离散化的破坏体。如图2所示,矩形断面被2n个关于Y轴对称的点离散分割,分别记作Aj和A′j,其中1≤j≤n。矩形隧道开挖面轮廓线上每一段的均分点数由各段长度加权算出,以此精确描述隧道开挖面轮廓。
2.2 破裂体空间离散
基于开挖轮廓上的2n个离散点,在满足Mohr-Coulomb屈服准则的基本假设下,以相邻2点作为初始点生成下一径向平面上的新点,以此类推,到F点结束,从而生成三维离散模型。
如图2所示,径向平面Πj由O,Aj和A′j3点确定,并与以O点为旋转中心的空间速度场正交。径向平面Π1,Π2…Πn与隧道开挖面相交,将这一区域定义为区域1;径向平面Πn后,由相邻径向平面绕X轴旋转固定离散角度δθ形成的径向平面定义为区域2。
区域1内径向平面Πj上直线OAj与Y轴方向的夹角θj可以表示为:
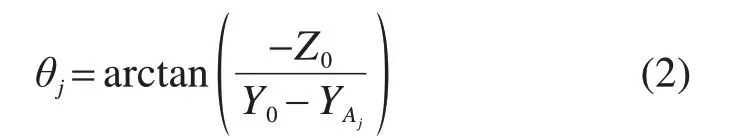
则,区域2内的夹角θj为:

建立局部平面坐标系(xj,Cj,yj),通过坐标系转换,Cj在空间直角坐标系(X,Y,Z)中的坐标为:

为更方便地对空间中各点的坐标进行表示,采用Pi,j表示空间中的点,i,j分别表示点在平面中的位置和径向平面在空间中的位置。矩形顶管隧道三维离散模型生成破坏面的基本思想是:通过径向平面Πj上2点Pi,j和Pi+1,j,生成相邻径向平面Πj+1上的新点Pi,j+1,这3个点组成破坏面上的一个微元三角形Fi,j,此外Pi+1,j,Pi,j+1和Pi+1,j+1构成一个微元三角形F′i,j,微元三角形也是后续功率计算时的最小单元。若干个微元三角形相连共同构成一个多面体来近似描述开挖面前方的土体破坏区,如图3。
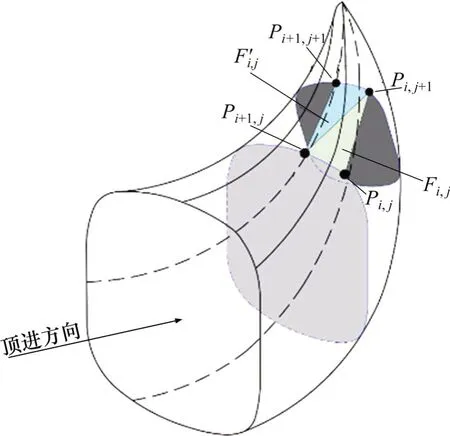
图3 点Pi,j+1生成机理3D示意图Fig.3 3D schematic diagram of point Pi,j+1 formation mechanism
在生成新点Pi,j+1的过程中,为保证Pi,j+1处于速度间断面上且符合Mohr-Coulomb屈服准则,需遵循以下3个原则:
1)微元三角形面Fi,j由点Pi,j,Pi+1,j和Pi,j+1组成,而且符合正交条件,这意味着指向机构外侧的单位向量N与面上的速度向量v j形成的夹角,φ为土体内摩擦角。该条件是为了保证整个机构符合运动学。
2)点Pi,j+1属于径向平面Πj+1,这是为了保证整个破坏面能够顺利生成。
3)开挖面轮廓线上取微元段研究时,径向平面Πj+1上生成的新点Pi,j+1近似接近线段Pi,j Pi+1,j的中点P′i,j,在局部坐标系中对应的角度θi,j+1是由Πj上Pi,j和Pi+1,j2点所对应的θi,j和θi+1,j求平均值得到,即θi,j+1=( )θi,j+θi+1,j/2,这是为了保证点均匀分布,能够较准确的描述破坏面。
基于上述的基本思想,可进一步得到区域1和区域2这2个区域上P点的生成机理,并可得到生成新点Pi,j+1的坐标:
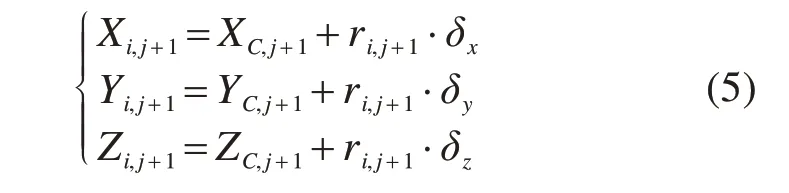
上述离散过程可采用计算机程序来实现,进而可通过空间上的各点可以描绘出矩形顶管隧道开挖面前方土体失稳破坏面。值得注意的是,在点生点形成开挖面前方破坏体的过程中,当达到以下2个条件时,破坏体上点将会终止生成。
1)当径向平面Πj+1的θj+1大于θF时,平面Πj+1整体位于F点以上;
2)当径向平面Πj+1上所有的点均位于地表以上时,判定破坏体超出地表。
3 失稳过程中外力做功与能量耗散计算
在矩形顶管隧道开挖面失稳破坏临界状态时,外力做的功率由土体的自重做功Wγ,孔隙水压力做功Wu和开挖面支护力做功WσT组成。而基于离散技术构建出的破坏机构由有限个离散微元组成,因此破坏体中各功率计算均由各个微元体对应功率叠加计算得出。
取图4所示的微元体进行分析,微元体面积的计算与平面Πj上的点Pi,j,Pi+1,j及相邻平面Πj+1上的点Pi,j+1,Pi+1,j+1有关。这4个点构成2个微元三角形,由这些微元三角形的面积累加可近似表示破坏面的表面积。

图4 微元体表面积计算示意图Fig.4 Schematic diagram of calculation of surface area ofm icroelement
如图4所示,三角形有2种划分方式。在图4(a)中,由点Pi,j,Pi+1,j和Pi,j+1与点Pi,j+1,Pi+1,j和Pi+1,j+1构成2个三角形,面积分别记作Sa与Sb;在图4(b)中,则是另一种组成方式,点Pi,j,Pi,j+1和Pi+1,j+1与点Pi,j,Pi+1,j和Pi+1,j+1构成2个三角形,面积分别记作Sc与Sd。则4个三角形的面积可由向量计算得到:
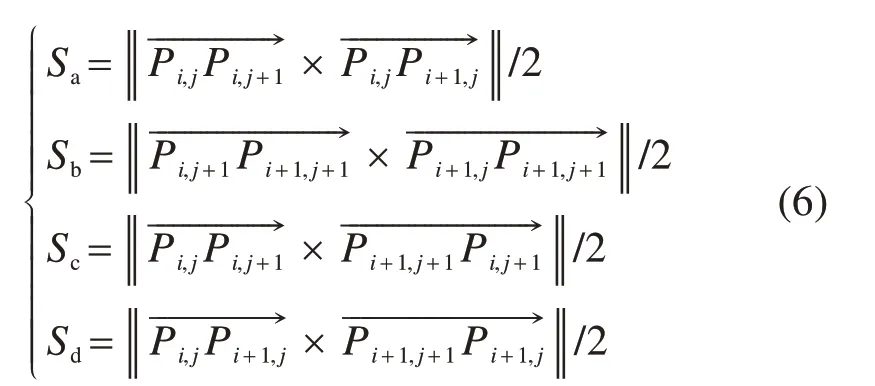
则由Pi,j,Pi+1,j,Pi,j+1,Pi+1,j+14点构成的微元体表面积为:
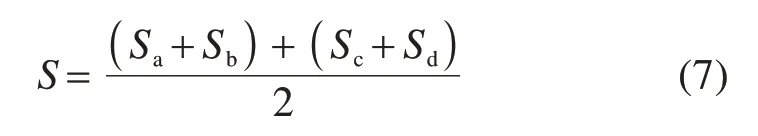
如图5所示,将Sa,Sb,Sc和Sd在YAZ对称面
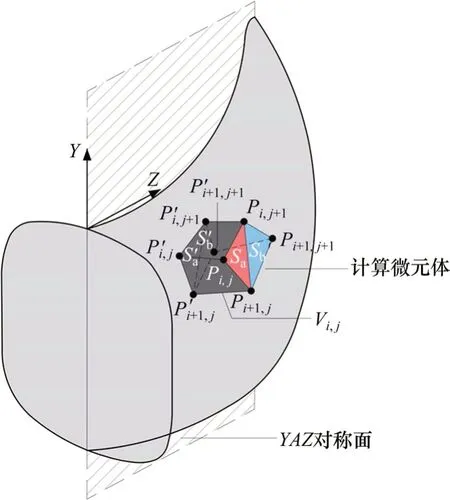
图5 微元体体积计算示意图Fig.5 Schematic diagram of cellvolume calculation
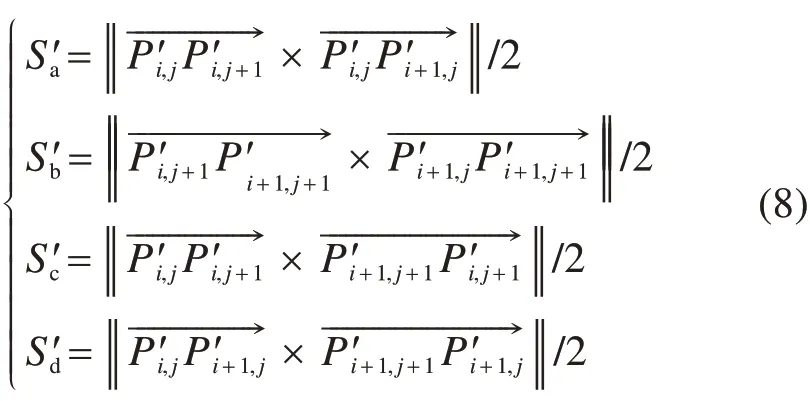
三角形Sa,Sb,Sc和Sd与平面YAZ上的投影和构成空间棱柱体Va,Vb,Vc和Vd,则各自的棱柱体体积计算式为:

综上,可求得微元体的体积V:
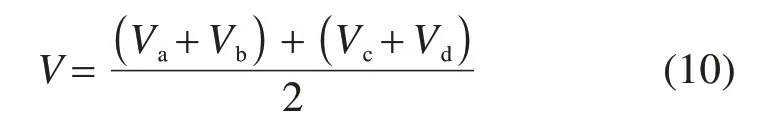
3.1 土体自重功率Wγ
破裂体的总重力功率为各个微元体的重力叠加计算得到,即:
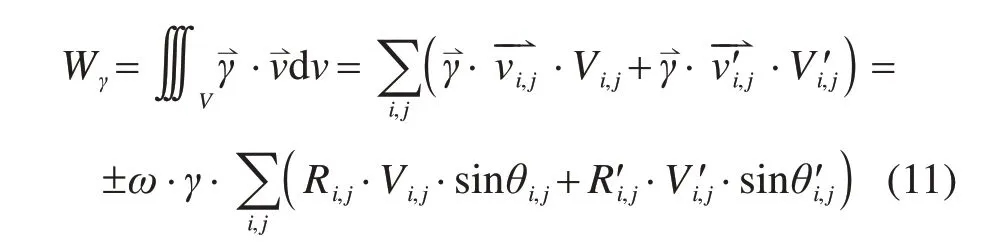
式中:Ri,j和θi,j(R′i,j和θ′i,j对称相等)是离散微元面Si,j为对称面)重心的极坐标。
在空间直角坐标系中Si,j重心坐标记作(XS i,j,YS i,j,ZS i,j),则Ri,j和θi,j为:

3.2 孔隙水压力功率Wu
在求解孔隙水压力做功时,做一定的简化处理。Bishop将孔隙水压力换算成与土体自重应力相关的计算公式[18]:

式中:u为孔隙水压力;ru为孔隙水压力系数;γ为土体容重;z为所求点到地下水位面的高度。
依据上限定理中破坏机制为一个忽略体积应变的刚性体的基本假设,在破坏过程中,孔隙水压力只在破坏体表面做功,同样是将破坏边界分割成微元面单元进行计算。则孔隙水压力功率计算如下式:

式中:n i为破坏面外法线单位向量;v i为速度场中的速度向量;S为破坏体机制的表面积。
3.3 开挖面支护压力功率WσT
计算开挖面支护压力功率时,计算微元是由开挖面轮廓线上Aj,Aj+1,A′j和A′j+1构成的四边形Σj,如图6。
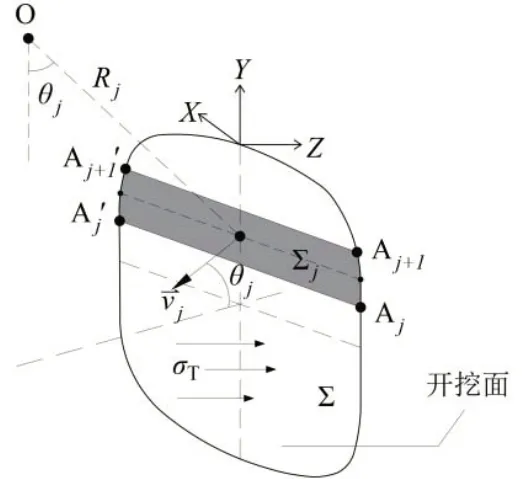
图6 矩形开挖面计算微元示意图Fig.6 Schematic diagram of calculatingm icro-elementof rectangularexcavation surface
则开挖面支护力做功功率为:
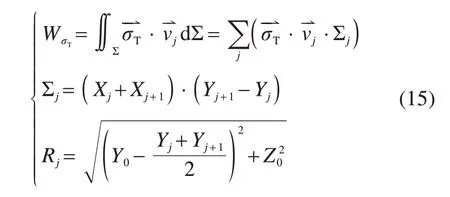
式中:Σj为开挖面计算微元四边形的面积;Rj为旋转中心O点到微元四边形Σj中心点的距离。
3.4 内能耗散率W D
依据开挖面前方破坏土体为刚体的假定,破坏机构的内能耗散沿着速度间断面上做功。能量耗散的本质是c∙δu,其中c为土体黏聚力,δu是速度微元在速度间断面上的切向分量。整个离散机构的内能耗散由各微元的能量耗散叠加求得:

式中:Ri,j为旋转中心O点到空间四边形微元体重心的距离;Si,j为空间四边形微元的面积。
综上,整个破坏机构的外力功率为:WE=Wγ+Wu-WσT,内能耗散率为WD,根据极限分析理论,建立不等式方程WD≥WE[16-17],可以求出开挖面的极限支护压力σT。在通过Matlab编程求解过程中,通过不断调整旋转中心O点的位置,循环优化直至求解出最小值,此解即为开挖面极限支护压力,计算流程如图7,程序编制过程不做赘述。
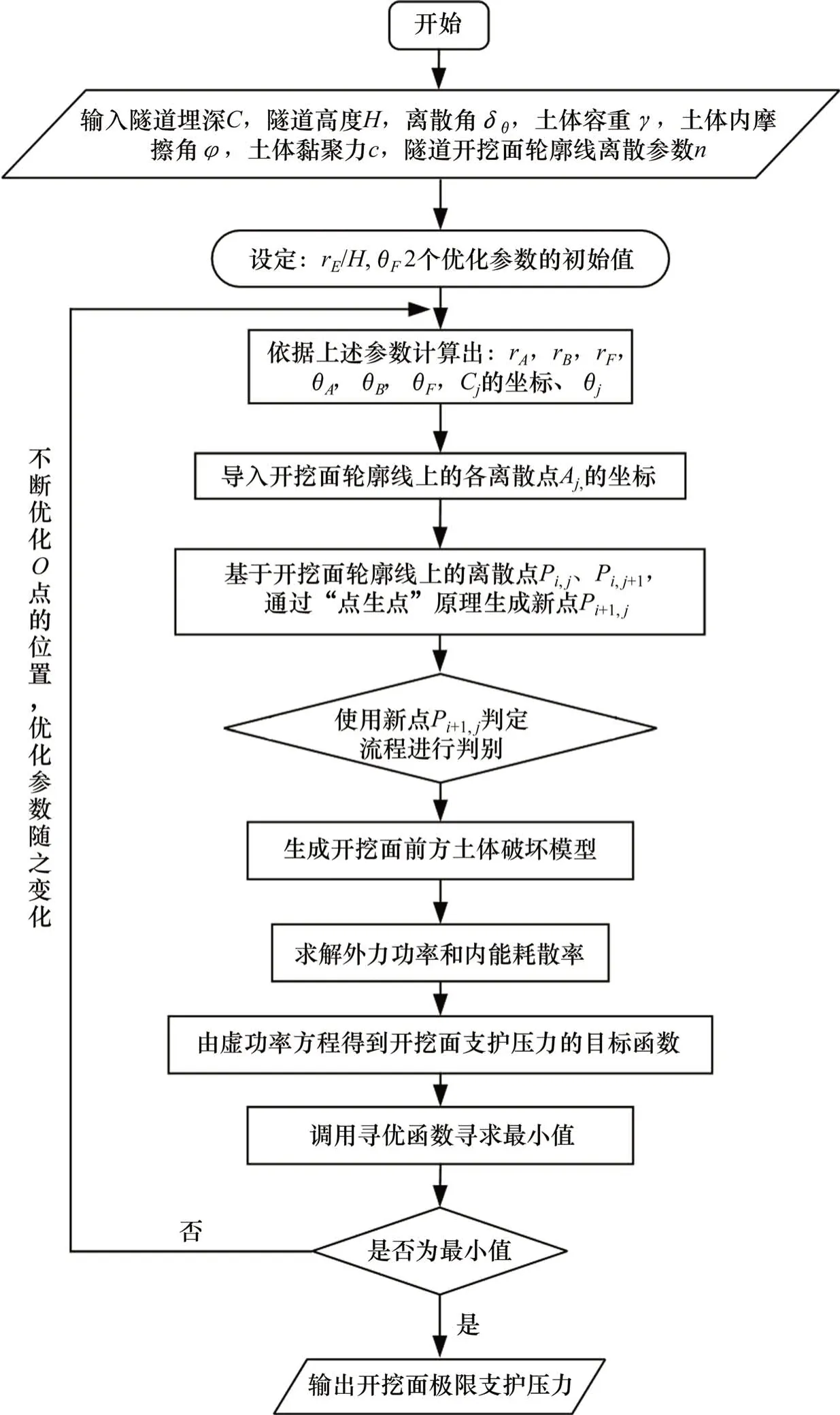
图7 开挖面极限支护压力求解流程图Fig.7 Flow chartof solving ultimate supportpressure of excavation face
4 实例验证与分析
4.1 红专路下穿中州大道顶管隧道
郑州市红专路下穿中州大道隧道工程是连接郑州新老城区的关键通道,隧道采用了土压平衡盾构式矩形顶管法施工,顶管段全长约105m,隧道平均埋深为4m,如图8,地层参数如表1[6-7]。

图8 郑州市红专路下穿中州大道顶管隧道平纵断面Fig.8 Horizontaland longitudinalsection of Hongzhuan Road pipe Jacking tunnel

表1 地层物理力学参数Table 1 Physicalandmechanicalparametersof formation
取图8中典型截面进行分析(如图9),将相关参数输入至根据第3节计算思路编制的程序中,得出和θE2个无量纲参数的最优解(39.771,6.472 8),进而确定旋转中心O点最佳位置的坐标为(0m,-8.51m,-5.68m),在此基础上生成三维破坏机制(如图10),便可得到矩形顶管隧道三维破坏机制的土体自重功率Wγ=1.33×104,内能耗散率WD=2.325×104,开挖面支护力做功功率WσT=9.95×103。由于不考虑地下水的作用,除土体自重外,外力中只有开挖面支护力做功,则可计算出开挖面极限支护压力为27.14 kPa,与现场监测的开挖面支护压力24.86 kPa相比,偏差约为8%。
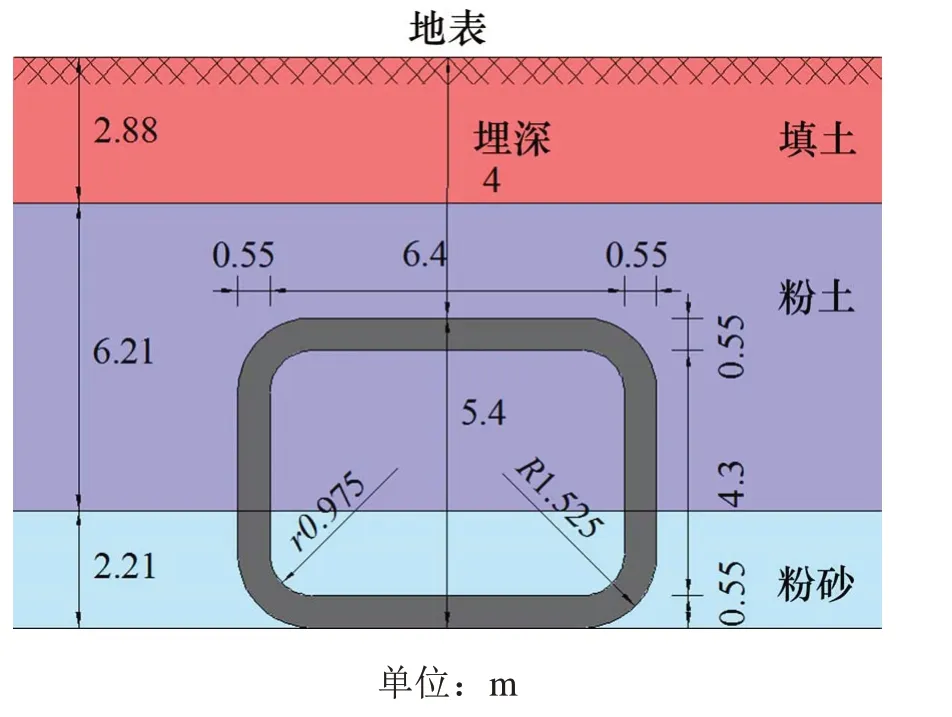
图9 地层-结构分布图Fig.9 Stratigraphic and structuraldistribution

图10 红专路矩形顶管隧道三维破坏机制Fig.10 Three-dimensional failuremechanism diagram of hongzhuan Road rectangular pipe jacking tunnel
4.2 南宁地铁5号线明秀站D号出入口通道
南宁轨道交通5号线1期工程明秀站位于友爱路与明秀路交叉口的东北角,D号出入口顶管隧道平面布置,全长约为55m,地质条件如图11和表2。采用顶管法施工和箱型预制混凝土管节。顶管掘进尺寸4.9m×6.9m,结构外尺寸6.9m×4.9m×1.5m,壁厚0.5m[2]。

图11 明秀站D号出入口工程地质和结构设计图Fig.11 Engineering geology and structural design draw ing of Entrance D of M ingxiu Station
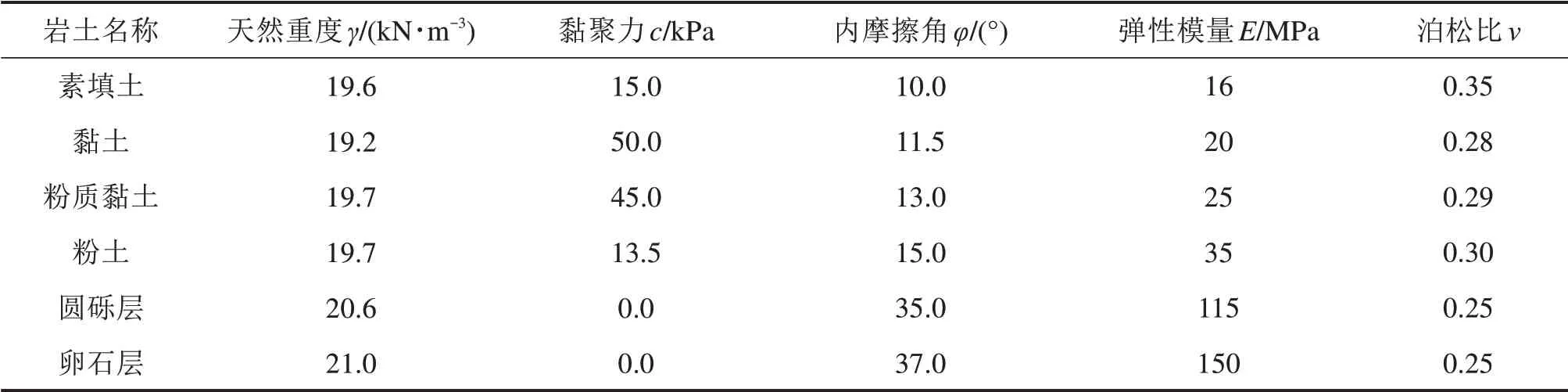
表2 工程地质参数Tab le 2 Engineering geological parameters table
取代表性断面进行分析,如图12。同案例1,将管节截面参数及各分层工程地质参数输入到程序运行计算,得出和θE2个无量纲参数的最优解(19.476,5.001 6),进而确定旋转中心O点最佳位置的坐标为(0,-0.85,-2.93m),在此基础上生成三维破坏机制(如图13),可得到考虑地层分层及地下水作用下的三维矩形顶管隧道的外力功率及内能耗散率。破坏机制的土体自重功率Wγ=1.55×104,内能耗散率WD=8.34×104,开挖面支护力做功功率WσT=5.61×104,孔隙水压力做功功率Wu=1.18×104,则可计算出开挖面极限支护压力为94.73 kPa,与现场监测的开挖面支护压力103 kPa相比,误差约为8%。

图12 地层-结构分布图Fig.12 Stratigraphic and structuraldistribution
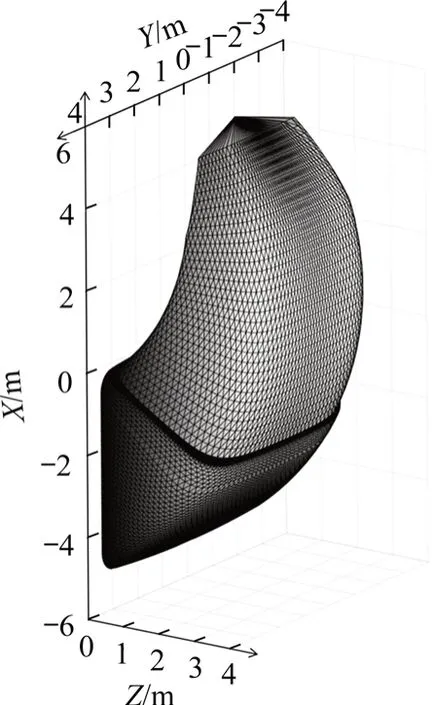
图13 南宁地铁5号线明秀站D号出入口破坏机制图Fig.13 Damagemechanism diagram of entrance D of M ingxiu Station of Nanning Metro Line 5
综合上述2个案例分析可见,本文所建立的矩形顶管开挖面失稳三维极限分析方法是可靠的,可指导顶管隧道的设计与施工。
5 结论
1)基于离散化技术,建立了矩形顶管隧道三维离散化分析机构,再基于逐点生成机理形成矩形顶管隧道三维破坏面,构建了矩形顶管隧道开挖面三维失稳破坏模型。
2)依据极限分析上限定理,结合矩形顶管隧道三维离散模型和速度场,推导出了矩形顶管隧道开挖面支护力的计算公式。并基于Matlab软件平台,调用Matlab内置寻优函数不断优化内置参数,实现了开挖面极限支护压力的计算。
3)结合2个工程实例开展模型可靠性验证,结果表明,本文所建立的大断面矩形顶管隧道开挖面稳定性三维极限分析方法计算结果与实测结果吻合较好,误差在10%以内,可指导设计与施工。
