考虑Hoek-Brown破坏准则的圆形隧道支护结构内力分析

2022-09-23杜佃春郭鹏

铁道科学与工程学报 2022年8期

杜佃春，郭鹏

(东南大学混凝土及预应力混凝土结构教育部重点实验室，江苏南京 211189)

近年来，我国在铁路建设方面取得了举世瞩目的成就。截止2020年底，全国铁路营业总里程达14.14万km，位居世界第二；其中高铁里程为3.6万km，居世界第一。中国国家铁路集团有限公司于2020年8月发布的《新时代交通强国铁路先行规划纲要》提到：要重点强化中西部地区对外通道，提升西部陆海新通道及煤运通道等能力。而我国中西部多以高原山地为主，这意味着隧道在线路的占比极高；以还未完全建成的川藏铁路为例，全线隧道占比超8成。本文拟考虑Hoek-Brown破坏准则(H-B准则)，对圆形隧道支护结构内力分布规律展开研究，以期给出一种可适用于计算相应圆形隧道内力的理论方法。隧道支护结构设计方法包括经验法、解析解法和数值法[1]。经验法是指依托工程实例，参考相应的岩石力学特性总结出的设计建议和规划方案，如BIEN‐IAWSKI[2]的RMR法和BARTON[3]的Q system法。该类方法通常适用于硬岩中开挖隧道的设计，在软弱围岩中应用时则存在明显不足。对于解析解法[4-9]，在应用时需要先评估周围岩石施加到衬砌结构上的外荷载，荷载大小既可利用经验解计算得到[10-11]，又可直接通过查询岩石的分类等级表来获取[12-15]。解析解法的局限性在于并未考虑周围岩石与支撑结构之间的相互作用。近年来，数值法因其可考虑复杂的隧道断面形式、岩石类型和围岩-结构间的相互作用而得到广泛应用[16-19]。然而三维数值模拟通常比较耗时，不利于隧道设计者在隧道设计初期开展大量的参数分析。因此，实际数值模拟分析中也会较多地采用平面应变条件下的二维(2D)数值模型来预测隧道开挖后引起的变形和应力重分布。现有文献中，可高效地给出考虑H-B破坏准则的圆形隧道衬砌结构内力分布规律的研究方法甚少。超静定响应法(Hyperstatic Reaction Method-HRM法)作为一种半解析半数值方法，通过虚拟的弹簧来模拟开挖隧道支护结构与周围岩体之间的相互作用，可高效地(3 s/次Intel CPU 2 GHz PC)计算出隧道衬砌结构的内力，尤其适用于隧道横截面设计分析[20-28]。ORESTE[20]以FEMSUP的形式首次将该方法引入到隧道行为分析中。之后，DO等[21]和DU等[22-23,25]分别将该方法扩展应用到圆形隧道考虑衬砌结点和非圆形隧道的行为分析中，上述研究均未考虑隧道在服从H-B破坏准则的围岩中的开挖工况。隧道设计与围岩强度参数密切相关，已有研究表明，隧道围岩的强度特性表现出明显的非线性[29]，其破坏包络线与设计中常用的线性Mohr-Coulomb破坏准则(M-C准则)并不一致。因此，本文基于HRM法从支护结构的弯矩和轴力方面来研究开挖围岩服从H-B破坏准则时的圆形隧道支护结构力学行为，进一步探究圆形隧道支护结构内力分布规律。通过将本文方法计算所得结果与经典方法给出的结果进行对比，验证了本文方法的有效性。随后，研究了不同的隧道埋深H，不同的无侧限抗压强度σci和地质强度参数GSI对隧道支护结构内力分布的影响。据此，本文给出了一种高效的圆形隧道支护结构内力分析方法，可为隧道设计初期支护结构的力学行为分析提供参考，为服从H-B破坏准则的岩体中开挖的圆形隧道支护结构设计提供理论依据。

1 广义H-B破坏准则及其等效M-C强度参数

1.1 广义H-B准则

为评估岩石的强度，HOEK等[30]介绍了广义HB强度准则，其表达式为：

其中，σ1和σ3分别表示最大和最小主应力；σci为岩石的无侧限抗压强度(0.01MPa≤σci≤200MPa)；mb，s和a均表示岩石属性参数，分别由下式计算得出：

其中，mi(5≤mi≤35)是岩石材料常数；D为岩石扰动因数，其取值范围0～1，取决于岩石的扰动程度[30-31]，D=0表示隧道开挖对周围岩石造成的扰动非常小。鉴于本研究集中于隧道支护结构的设计，在本研究中均取D=0。GSI(Geological Strength Index)是用来描述岩石变形与强度的指标[32]，可根据岩石的地质情况来确定GSI取值(5≤GSI≤100)。

弹性模量是描述材料强度的重要参数，岩石的弹性模量Erm(MPa)可由HOEK等[33]提出计算式求得：

当σci≤100MPa

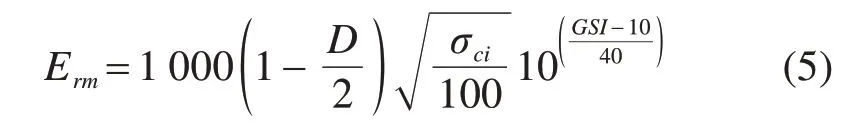
当σci>100MPa

根据剪切模量和弹性模量之间的关系，则得到岩石的剪切模量Grm，MPa：

其中：vrm是岩石的泊松比，其变化范围在0.1到0.3之间[34]，本研究中vrm取值为0.3。

1.2 等效M-C强度参数

在隧道设计中，开挖围岩的黏聚力c和摩擦角φ是较常用到的参数。HOEK等[33]给出了服从H-B破坏准则的岩石的等效黏聚力c′和等效摩擦角φ′的表达式，分别为：

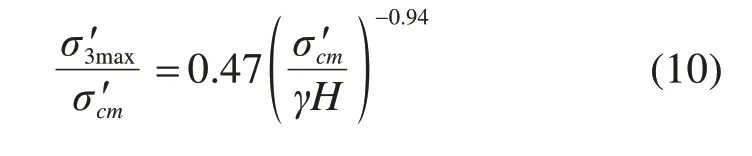
其中：γ是岩石的重度；H为隧道的埋深。当水平应力高于竖向应力时，式(10)中的γH应替换为水平应力值。表示岩体的强度，其计算式为：

本文基于超静定响应法对在服从H-B破坏准则的岩体中开挖的深埋圆形隧道支护结构内力展开分析，将采用由式(8)和式(9)给出的等效M-C强度参数进行计算。

2 HRM法简介

HRM法作为一种半解析半数值法，已经被众多学者成功应用于隧道设计中[20-28]。在该方法中，衬砌结构被划分为有限个数量的梁单元，单元与单元之间是通过结点建立联系，而衬砌结构与开挖围岩之间的相互作用则是通过分布于结点上的轴向与切向弹簧来实现的。本文假定隧道所受的荷载分布形式如图1所示，其中σv表示围岩施加到衬砌上的竖向主动荷载，由σv=γH计算得到[10]；γ为岩石重度；H为隧道埋深；σh为水平主动荷载，其计算表达式为σh=K0σv，其中K0为围岩侧压力系数；kn和ks分别表示弹簧的轴向和切向刚度；R是隧道开挖半径；EI和EA分别表示衬砌的抗弯和抗压刚度；X和Y是整体笛卡尔坐标系坐标。

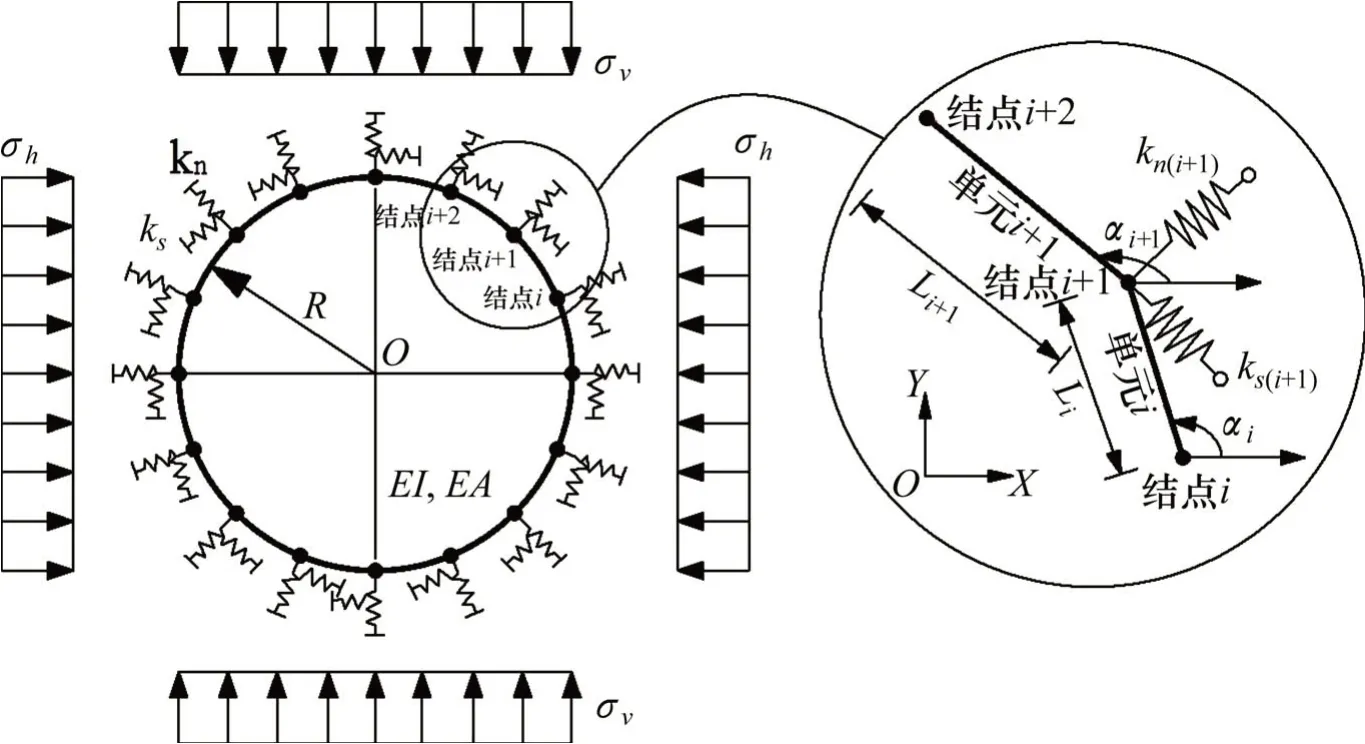
图1 HRM法中单元离散图示Fig.1 Calculation scheme of the supportusing the HRM method

图2为HRM方法中假定的梁单元示意图，其中h为单元初始端结点，j为单元末端结点，u表示轴向位移，v代表切向位移，θ是结点旋转角，Li为单元长度，x和y是局部笛卡尔坐标系坐标。隧道衬砌结构是通过结点上的弹簧与开挖围岩建立联系的，一旦结点位移已知，即可得到每个梁单元上的内力及位移分布特征。因此，应用HRM方法求解衬砌结构内力和位移分布形式的关键是要确定结点的位移量。结点位移量可以通过定义整体笛卡尔坐标系下的结构单元总体刚度矩阵K，通过式(12)计算：

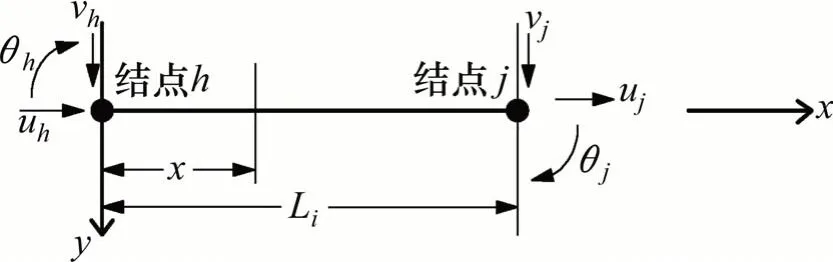
图2 局部坐标下的梁单元示意图Fig.2 Beam-type elementw ith reference to the local cartesian coordinates

其中F=[F1,F2,…,Fn]T表示结点上的力向量(如图1中围岩施加到结构上的外主动荷载σv和σh)。同理，S1,S2,…,Sn是由每个结点的3个位移量组成的位移子向量。

总的刚度矩阵K可以通过整体笛卡尔坐标系下所有单元的局部刚度矩阵集合得到，用ki表示第i个单元(i=1,2,3,…,360)的局部刚度矩阵。总的刚度矩阵K的表达式如下：

其中：表示局部笛卡尔坐标系下的局部刚度矩阵；λi是坐标转换矩阵。和λi的表达式分别如下：

式中：αi表示单元(i)与水平方向的倾角。

将式(13)～(16)代入式(12)可得到整体坐标系下全部结点的位移向量S，利用坐标转换得到局部笛卡尔坐标系下每个结点位移量，最终得到整个衬砌结构上的应力和位移值。

轴向弹簧刚度(kn)和剪切弹簧刚度(ks)计算式如下：

式中：Li是单元的长度，见图2。η*表示岩石施加到衬砌结构上的表观刚度，可由p/δ计算得到。本文采用ORESTE[20]介绍的响应压力p和支撑变形δ的关系式(见图3)，其表达式如下：

图3 围岩响应压力p和支撑结构变形δ之间的非线性关系Fig.3 Non-linear relationship between the reaction pressure p and the supportnormaldeformation

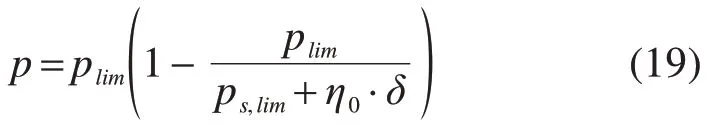
其中，最大轴向响应压力pn,lim为：

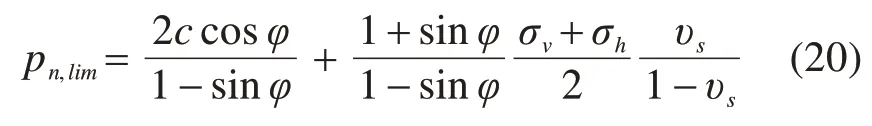
其中，c，φ和vs分别为围岩的等效黏聚力、等效摩擦角和泊松比。而初始轴向刚度表达式为：

式中：βs表示无量纲的尺寸因数；Es表示围岩的弹性模量；R为隧道半径。

3 与解析解的对比验证

为验证提出方法的有效性，将本文HRM解与已有的经典解析解进行了对比。ERDMANN[4]给出了求解圆形隧道支护结构最大内力值的解析解方法，其中最大轴力值Nmax和最大弯矩值Mmax求解公式分别为：

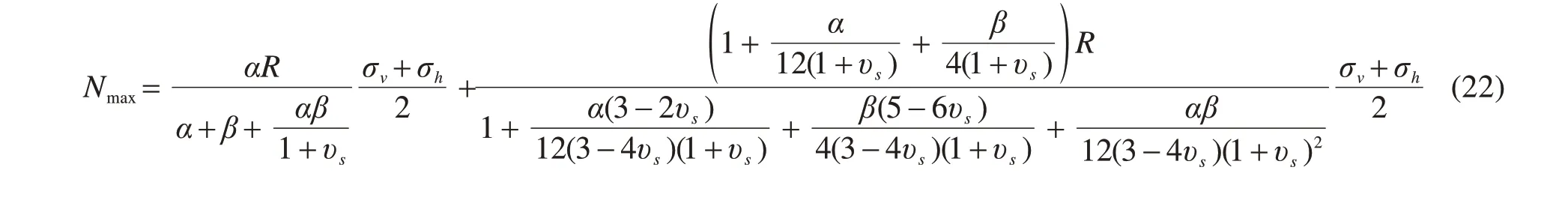
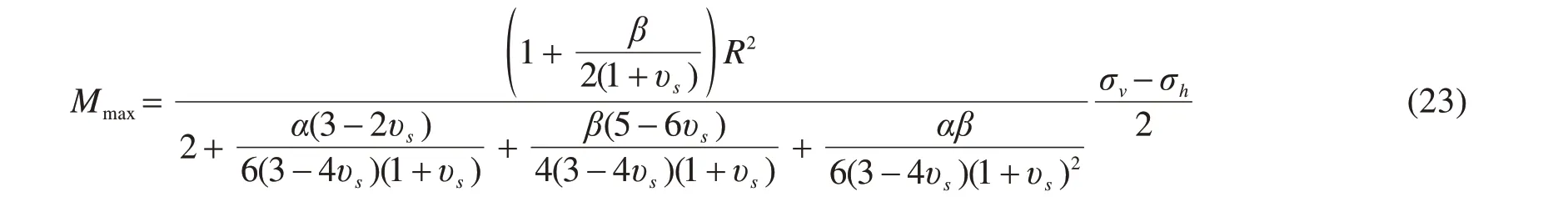
式中：α和β为相对刚度，可分别由下式计算得到：

式中：EI和EA分别为衬砌结构的抗弯和抗压刚度；Es为岩石的弹性模量。隧道衬砌结构弯矩和轴力正方向如图4所示，θ表示单元对称轴与竖直方向的夹角。

图4 隧道衬砌结构内力正方向示意图Fig.4 Positive direction of the structural forces(bendingmoment M,normal force N)

表1给出了本文HRM方法和ERDMANN[4]解析法计算得到的弯矩M和轴力N结果。计算中假定衬砌厚度t=0.5m，弹性模量E=29.5 GPa，隧道半径R=6.0m，岩石单位重度γ=25 kN/m3，H-B准则参数分别为σci=50 MPa，mi=10，GSI=50，D=0，隧道埋深H=40m，侧向土压力系数K0=0.5。

由表1可知，HRM方法计算得到的弯矩结果稍大于ERDMANN[4]所得结果，且两者误差绝对值小于0.5%，2种方法所得轴力值误差在0.1%内，该对比验证了本文方法的有效性。

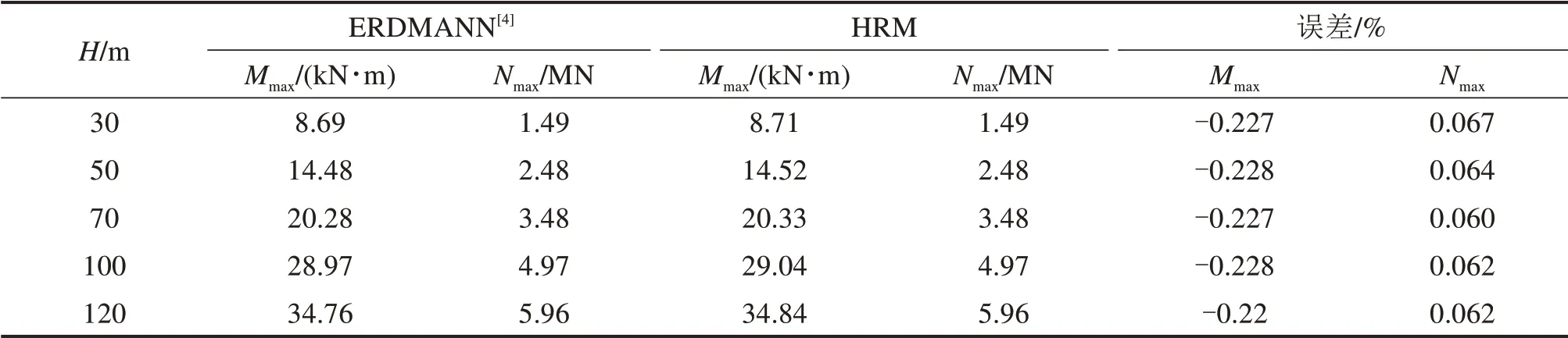
表1 不同隧道埋深下隧道衬砌结构内力最值结果对比Tab le 1 Comparison of the HRM and ERDMANN[4]resultsw ith different tunnel depth

4 影响因素分析

本节分别给出了不同隧道埋深H，H-B强度准则参数σci和GSI对圆形隧道衬砌内力(轴力和弯矩)分布的影响，所得结果可为在服从Hoek-Brown破坏准则的岩体中开挖的圆形隧道支护结构内力分析提供参考。

4.1 隧道埋深的影响

为研究圆形隧道埋深对衬砌结构内力的影响，计算参数取值如下：t=0.5 m，E=29.5 GPa，R=6.0 m，γ=25 kN/m3，σci=50 MPa，mi=10，GSI=50，D=0，K0=0.5，隧道埋深H分别取30，50，70和100m。

隧道埋深对圆形隧道衬砌内力影响如图5所示。由图5可知，隧道埋深对结构内力的影响十分明显。隧道埋深越大，弯矩和轴力值越大，如在隧道拱顶处，当隧道埋深从30m增加到100m时，弯矩值从8.7(kN∙m)/m增加到29.0(kN∙m)/m，而轴力值则从0.76MN/m增加到2.54MN/m；弯矩最大绝对值发生在隧道拱顶、侧墙和拱底处，而最大轴力值发生在隧道侧墙处。这是因为，隧道埋深越大，施加到衬砌结构上的外荷载越大。因此，衬砌结构的内力随埋深增加而增大。

图5 隧道埋深对衬砌结构内力的影响Fig.5 Effectof the tunneldepth H on the internal forcesof tunnel lining

4.2 岩石无侧限抗压强度的影响

为研究岩石无侧限抗压强度对圆形隧道衬砌结构内力的影响，计算参数取值同4.1部分。隧道埋深H=50m，岩石无侧限抗压强度σci分别取10，25，50，75和100MPa。

岩石无侧限抗压强度σci对圆形隧道衬砌内力影响如图6所示。由图6可得，σci对结构内力的影响十分明显。随着σci增大，弯矩和轴力值逐渐减小。如在隧道拱顶处，当无侧限抗压强度从10MPa增加到100MPa时，弯矩值从35.5(kN∙m)/m减小到9.6(kN∙m)/m，而轴力值则从2.28MN/m减小到0.92MN/m。这是因为岩石的无侧限抗压强度越高，隧道开挖后围岩的自稳定性越好，引起的结构内力则越小。不同σci值引起的衬砌结构的弯矩最大绝对值仍发生在隧道拱顶、侧墙和拱底处，最大轴力值仅出现在隧道侧墙处。

图6 岩石无侧限抗压强度σci对圆形隧道衬砌内力影响Fig.6 Effectof the unconfined compression strength of the rockmassesσci on the internal forcesof tunnel lining

4.3 GSI的影响

本小节给出了岩石地质强度参数GSI对圆形隧道衬砌结构内力的影响，计算参数取值同4.1部分，隧道埋深H=50m。GSI取值接近于10时意味着岩石破碎程度极高，当GSI取值接近于100时表示岩石完整性极好，而CARRANZA-TORRES等[16]指出隧道开挖扰动后的围岩完整性降低，意味着GSI取值应当小于100。因此，研究中GSI分别取值为30，40，50和60。得到岩石地质强度参数GSI对圆形隧道衬砌内力影响规律如图7所示。

从图7中可以看出，GSI对结构内力的影响十分明显。GSI值增大，弯矩和轴力值越小。这是因为当围岩GSI越大，隧道开挖后岩石完整越好，围岩的整体自稳定性越好，使得衬砌结构内力越小。在隧道拱顶处，当GSI从30增加到60时，弯矩值从51.2(kN∙m)/m减小到7.2(kN∙m)/m，而轴力值则从2.72MN/m减小到0.69MN/m。类似地，不同GSI值引起的衬砌结构的弯矩最大绝对值出现在隧道拱顶、侧墙和拱底处；而最大轴力值仅出现在隧道侧墙处。