大坡道桥上无砟轨道梁端过渡板力学性能分析

张鹏飞，温月，涂建，陈华鹏

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

桥上无砟轨道无缝线路在高速铁路建设中得到越来越广泛的应用[1]，位于坡道上的桥梁铺设无砟轨道时，桥梁梁体以及轨道结构易因温度荷载作用产生伸缩变形[2-3]，使得梁端出现竖向错台现象，在其他外界荷载叠加作用下可能导致梁端附近扣件超限受力甚至破坏，严重影响行车安全。因此，研究梁端轨道结构在不同影响因素下的力学特性，对避免其超限破坏，延长无缝线路使用寿命，提高线路整体平顺性具有重要意义。冯玉林等[4]通过建立反映轨道形位变化的解析模型，对桥梁梁端转角工况下扣件系统受力进行了深入分析。勾红叶等[5]建立了无砟轨道-桥梁通用映射解析模型和空间实体有限元模型，研究了梁端竖向错台对轨道结构的影响。部分学者针对温度荷载作用下桥梁梁体位移开展了一系列研究，曲村等[6]建立桥梁纵横垂向有限元模型，对温度荷载下梁缝处的纵向变化量进行了计算。张志超等[7]分析了大跨度连续梁桥桥梁及轨道结构受力和位移在不同梁体温度下的变化规律。DING等[8]利用长期环境条件变化下桥梁伸缩缝位移实测数据，分析解释了温度对伸缩缝位移的影响。M IAO等[9]通过建立大跨度桥梁伸缩缝位移与主导环境因素的多元线性回归模型，得到温度是影响位移的主导因素。此外，还有学者针对在桥缝处设置过渡板改善轨道结构受力进行了相关研究，成果显著。赵忠洋等[10-11]提出高速铁路路桥过渡段设置搭板结构可以减小轨道因路基刚度突变产生的折角，提高轨道平顺性，减小过渡段轨道结构的受力。徐浩等[12]提出在桥梁铺设无砟轨道时，采用过渡板设计方案防止梁端扣件受力破坏。王平等[13]利用有限元法建立存在坡度的简支梁计算模型，分析了位于坡道上的桥梁梁端铺设过渡板后轨道结构扣件系统的受力情况。本文基于有限元法建立大坡道桥上CRTSⅢ型板式无砟轨道无缝线路梁端过渡板结构空间精细化有限元模型，分析了梁端增设过渡板情况下桥梁梁体温差、温度跨度以及纵向坡度作用下扣件、钢轨和轨道板的力学性能，研究成果可为大坡道桥上无砟轨道无缝线路梁端轨道结构安全服役和运营维护提供理论指导和技术支持。

1 精细化有限元建模

本文以大坡道桥上CRTSⅢ型板式无砟轨道无缝线路简支梁桥和连续梁桥为研究对象[14]，在梁端增设过渡板结构，其力学分析模型如图1所示。在此基础上，基于有限元法和梁-板-轨相互作用机理建立梁端过渡板结构空间精细化有限元模型，在桥梁两端分别设置50m的路基段，对无缝线路进行约束，消除边界效应对梁端轨道系统受力状况的影响；在进行有限元网格划分时，充分考虑各轨道、桥梁结构的细部尺寸及温度梯度荷载施加精度要求，保证各轨道和桥梁单元网格划分细致整齐，提高模型计算结果的精确性，梁端过渡板结构空间耦合模型如图2所示。

图1 桥上CRTSⅢ板式无砟轨道梁端过渡板力学分析模型Fig.1 Mechanicalanalysismodelof CRTSⅢslab Ballastless track beam-end transition slab on bridge

图2 梁端过渡板结构空间耦合模型Fig.2 Spatial couplingmodelof beam-end transition slab construction

1.1 模型单元及参数

在计算模型中，其参数取值及单元选择如下：

1)钢轨采用60 kg/m的标准钢轨(CHN60钢轨)，在空间耦合模型中CHN60钢轨采用Timoshenko梁(BEAM 188梁)单元模拟。

2)扣件采用WJ-8型常阻力扣件，间距为0.63m。扣件纵向阻力采用非线性弹簧单元COM‐BIN39进行模拟，根据式(1)和图3取值，用于钢轨和轨道板结构之间的连接。本计算模型采用无载条件下扣件阻力，取值为15 kN/组。

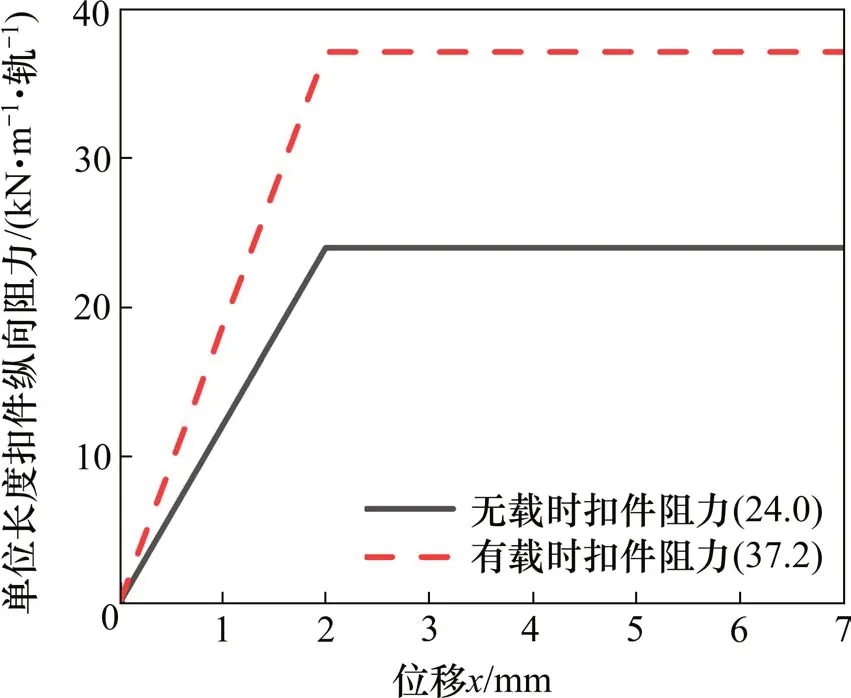
图3 扣件纵向阻力Fig.3 Longitudinal resistance of fastener

式中：r表示单位长度扣件阻力；x表示钢轨与扣件的纵向相对位移。

无砟轨道桥梁结构垂向受力受扣件系统刚度的影响很大，扣件系统竖向刚度具有明显非线性特征(式(2))，扣件节点刚度理论曲线如图4所示，其竖向受力状态可分为3个阶段[12-13]，扣件初始扣压力F0，弹性垫板刚度Kp和弹条刚度Ks对它的影响很大，扣件的∆y为扣件弹条竖向伸缩量。

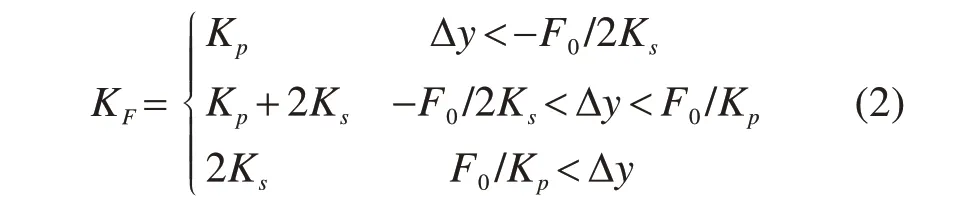
表1 扣件参数Table 1 Parameter table of fastener

第1阶段：钢轨受到的压力较大，扣件系统节点弹性仅由弹性垫板提供，扣件系统刚度为Kp。

第2阶段：随着钢轨受到的压力逐渐减小，钢轨逐渐脱离弹性垫板，但还未脱离，此时扣件系统刚度由弹性垫板和弹条共同提供为Kp+2Ks。

第3阶段：钢轨受到的拉力较大，钢轨与扣件弹性垫板脱开，扣件系统刚度由弹条提供为2Ks。

扣件采用的竖向刚度曲线如图4所示，扣件初始扣压力为18 kN，弹性垫板刚度为30 kN/mm。

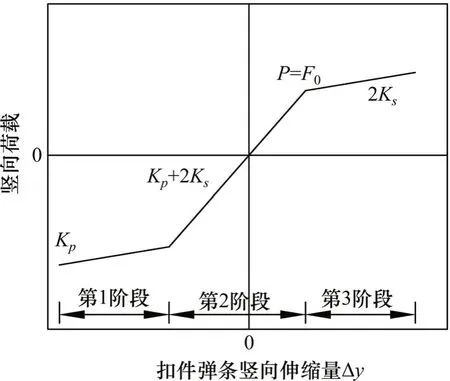
图4 扣件垂向刚度曲线Fig.4 Verticalstiffness curve of fastener

3)轨道板采用CRTSⅢ型板，轨道板结构、自密实混凝土层、底座板、过渡板、桥梁的尺寸及参数见表2，相邻底座板之间设置20mm的伸缩缝，桥梁、轨道结构、过渡板和弹性垫层均采用实体单元Solid45模拟，其中弹性垫层的弹性模量取25MPa。轨道板与自密实混凝土层、自密实混凝土层与凸台、凸台与弹性垫层、弹性垫层与凹槽结构间的接触为共用节点连接，自密实混凝土层与底座板间的隔离层采用非线性弹簧单元模拟，最大摩擦因数取0.70[15]。

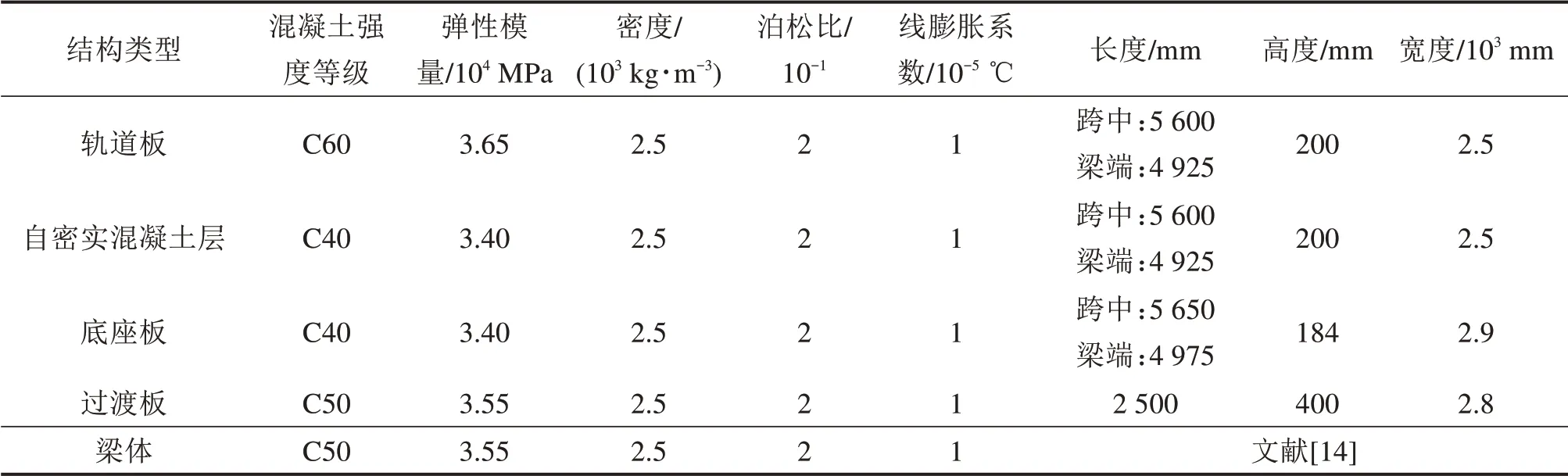
表2 桥梁与轨道结构参数取值Table 2 Parametervalue table of bridge and track structure

4)桥梁、过渡板支座纵向刚度和垂向刚度采用线性弹簧单元模拟，根据《高速铁路设计规范》[16]，过渡板支座纵向刚度取60 kN/mm。简支梁桥桥墩纵向刚度取350 kN/mm[14]，连续梁桥桥墩纵向刚度根据温度跨度换算。

1.2 模型验证

为了验证模型的正确性，本节采用上述方法建立2跨32m简支梁桥上无砟轨道空间有限元模型，与文献[13]中建立的位于坡道上32m简支梁梁端扣件有限元模型进行扣件受力对比，计算在简支梁桥梁梁体降温30℃时，桥梁纵向坡度取0‰，10‰，20‰和30‰4种工况下，本节建立模型与文献[13]中模型所计算的扣件受力数值对比情况，如图5所示。

如图5所示，本节梁端扣件受力分布规律与文献[13]基本一致，所选取梁缝两端扣件受力数值大致相同，扣件受力最大值之间的误差为3.2%，处于允许范围之内，说明本文所建模型能够准确计算出大坡道桥梁在温度荷载下梁端扣件受力情况，验证了本文模型的准确性。

图5 不同坡度下梁端扣件受力Fig.5 Stressanalysisof fasteneratbeam-end under differentslope

2 梁端过渡板结构力学性能分析

本节主要针对大坡道桥梁梁端结构，探讨增设过渡板对于梁端轨道结构受力的影响情况，通过对比在不同梁体温差下增设过渡板前后梁端轨道结构力学性能的变化，对过渡板结构的性能进行说明。

2.1 梁端轨道结构力学性能指标

梁端轨道结构力学性能主要通过扣件上拔力、扣件下压力、钢轨附加应力以及梁端轨道板稳定性来体现，本文所选取与上述力学性能对应的指标分别是：扣件拉力、扣件压力、钢轨弯曲应力和轨道板稳定系数。其中轨道板稳定系数需在有限元模型仿真所得数据基础上进行进一步计算，其计算公式见式(3)，过程如图6所示。

图6 轨道板稳定性计算图示Fig.6 Diagram for stability calculation of track slab

其中：G表示轨道板自重；L表示支座间的距离；F1，F2和F3表示扣件上拔力；F4和F5表示扣件下压力；Mz=G∙L/2；Ms=F1L1+F2L2+F3L3-F4L4-F5L5；M z表示轨道板自重产生的稳定力矩；M s表示扣件附加力产生的倾覆力矩；K表示轨道板稳定系数。

2.2 过渡板结构力学性能分析

《铁路无缝线路设计规范》[17]规定无砟轨道桥梁最大温差取30℃，《高速铁路设计规范》[16]规定动车组走行线路的最大坡度为35‰。

本节中桥梁纵向坡度取35‰，桥梁温度荷载分别考虑0℃，5℃，10℃，15℃，20℃，25℃和30℃这7种工况情况，对比温度跨度为88m的大跨度桥梁梁端增设过渡板前、后扣件受力、钢轨最大弯曲应力和轨道板稳定系数的变化情况。梁端竖向位移一般只对梁缝处6～8组扣件受力有影响[18]，因此，本文中扣件受力数值取自梁缝左右两侧各6个扣件。在7种工况情况下的最大扣件受力、钢轨弯曲应力和轨道板稳定系数如图7～9所示。

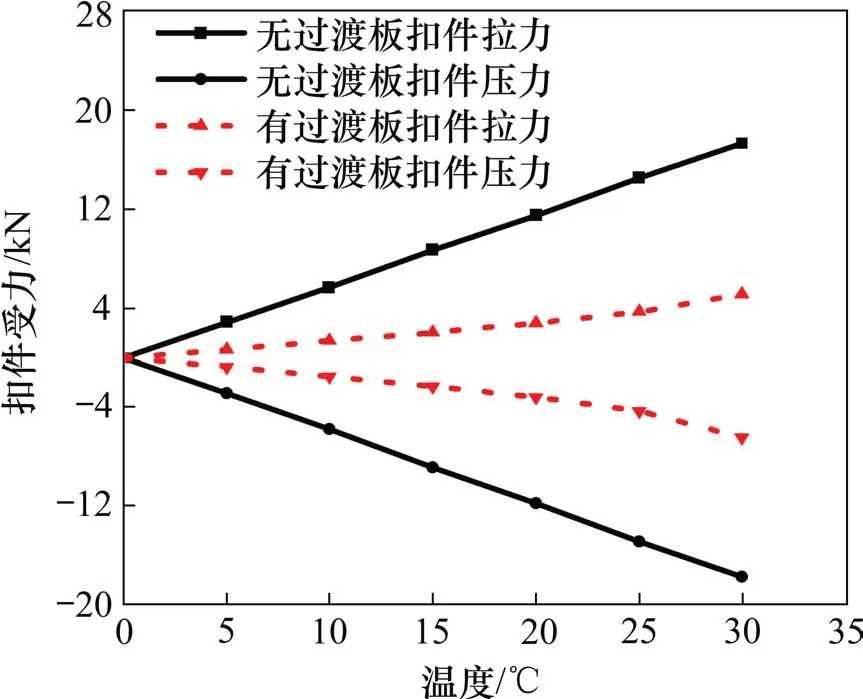
图7 不同桥梁梁体温差下扣件最大受力Fig.7 Maximum stressof fastenerunder differentbeam of bridge temperature difference

由图7～9可知，对于桥梁梁端无过渡板结构，当梁体温度荷载为30℃时，扣件最大拉力和最大压力分别是17.368 kN和17.776 kN，扣件最大拉力接近扣件最大压力；轨道板稳定系数为2.744，接近轨道板最小稳定系数1.3[18]。相比于无过渡板结构梁端轨道结构的受力情况，设置过渡板后，梁端轨道结构钢轨最大弯曲应力和梁端扣件受力有明显减小，最大弯曲应力减少了64.0%～64.9%，扣件最大拉力和最大压力分别减少了70.6%～76.8%和63.6%～74.3%；轨道板最小稳定系数增大了429%～769%，稳定性增强，梁端轨道结构受力得到明显改善。在桥梁梁体温度处于5℃～30℃区间内时，无论桥梁梁端是否增设过渡板结构，梁端扣件最大拉力和最大压力均随着桥梁梁体温度升高而近似线性增大，增长幅值比较稳定。

图8 不同桥梁梁体温差下钢轨弯曲应力Fig.8 Railbending stressunder differentbeam of bridge temperature difference

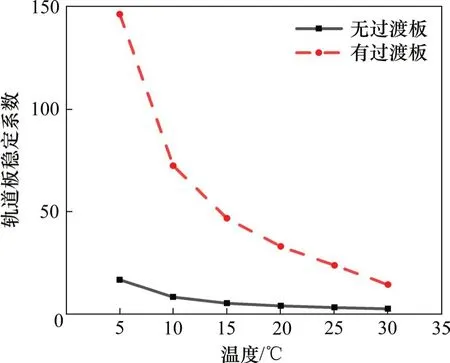
图9 不同桥梁梁体温差下轨道板稳定系数Fig.9 Stability coefficientof track slab under differentbeam ofbridge temperature difference

综上，大坡道桥梁梁端设置过渡板结构能够较大程度地改善梁端扣件、钢轨和轨道板受力情况，提高无缝线路的稳定性。

3 梁端轨道结构力学性能影响因素分析

本节针对增设过渡板的大坡道桥梁梁端轨道结构，研究其在不同影响因素下的力学性能变化情况。

3.1 桥梁梁体温差的影响

位于坡道上的大跨度桥梁，桥梁梁体会因温度变化发生纵向伸缩导致梁端竖向变形，从而导致梁端扣件附加上拔(下压)力的产生，同时在钢轨支点处产生附加弯矩，影响梁端扣件受力。由图7～9可知，梁体温差越大，梁端扣件受力越大，轨道板稳定系数越小，梁端扣件最大拉力和最大压力均随着桥梁梁体温差增大而线性增大，因此，在进行梁端轨道结构设计与养护时要充分考虑桥梁梁体温差的影响。

3.2 桥梁温度跨度的影响

位于坡道上的大跨度连续梁桥，当梁体温度受外界环境影响发生变化时，会产生不同的桥梁温度跨度，导致梁体纵向伸缩变形不同，从而导致梁端竖向相对位移也不同，对梁端轨道结构受力产生影响。本节连续梁桥纵向坡度分别取0‰，10‰，20‰，30‰和35‰，梁体温度升高25℃，分析连续梁桥增设过渡板后，不同温度跨度(表3)下梁端扣件受力、钢轨最大弯曲应力、轨道板稳定系数的变化情况，5种工况下最大扣件受力、钢轨弯曲应力和轨道板稳定系数如图10～12所示。

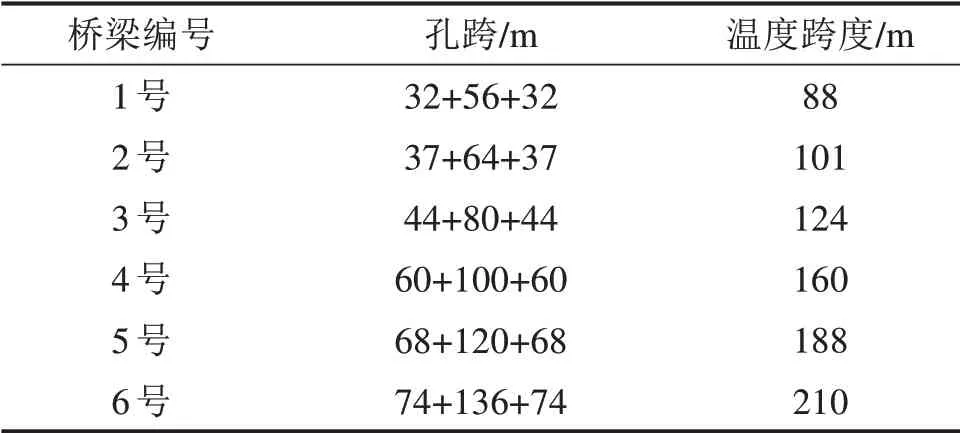
表3 不同跨度桥梁荷载取值Table 3 Load value of differentspan bridges

由图10和图11可知，当连续梁桥位于坡道上时，在不同桥梁梁体温度跨度下，桥梁梁端处扣件最大拉力、最大压力随着桥梁温度跨度的增加而增加，且最大扣件压力与最大扣件拉力近似相等，在坡度为20‰，桥梁温度跨度由88m增加至210m时，扣件最大拉力和最大压力分别增大了2.4倍和2.5倍。桥梁梁端的钢轨弯曲应力随桥梁温度跨度的增加而线性增大。对于扣件最大拉力、最大压力和钢轨弯曲应力，温度跨度越大，产生的影响越大。当桥梁坡度为0，桥梁温度跨度在88～210m范围内时，由于不同温度跨度引起桥梁纵向变形导致的梁端变形很小，梁端处扣件最大压力、最大拉力、钢轨最大弯曲应力均很小。

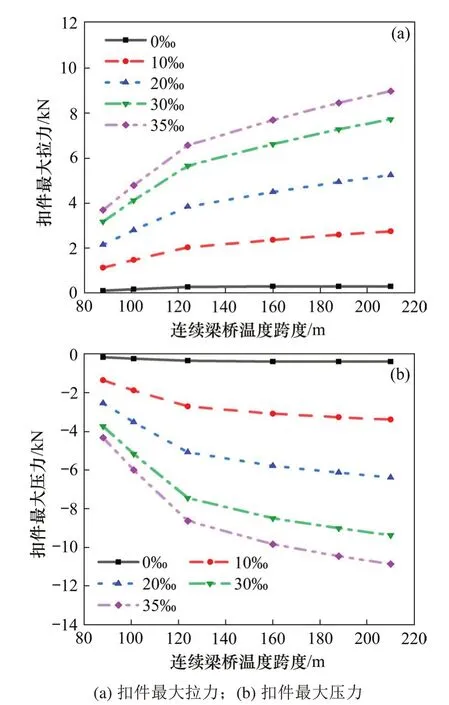
图10 不同桥梁温度跨度下扣件最大受力Fig.10 Maximum stressof fastenerunder differentbridge temperature span

图11 不同桥梁温度跨度下钢轨弯曲应力Fig.11 Bending stressof railunder differentbridge temperature span

由图12可知，当桥梁纵向坡度为0，桥梁温度跨度在88～120m范围内时，轨道板稳定系数变化较大，而桥梁存在坡度的情况下，温度跨度对于轨道板稳定系数产生的影响很小。

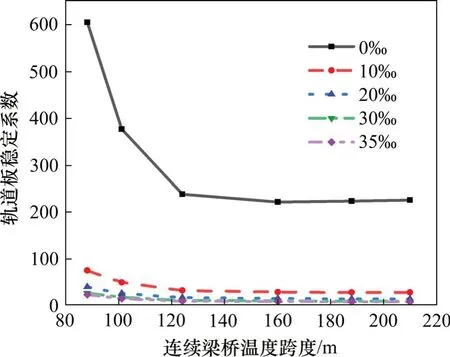
图12 不同桥梁温度跨度下轨道板稳定系数Fig.12 Stability coefficientof track slab under different bridge temperature span

综上所述，在坡度较大的区域进行桥上无砟轨道铺设时，应尽量选择简支梁桥或小跨度的连续梁桥，对于坡度较小的区域进行铺设时，可以选择大跨度连续梁桥。

3.3 桥梁梁体纵向坡度的影响

桥梁梁体纵向坡度对梁端轨道结构受力同样有着较大影响，因此本节取连续梁桥桥体温度升高25℃，纵向坡度分别取0‰，10‰，20‰，30‰和35‰这5种坡度工况，分析桥梁梁端增设过渡板结构后，不同坡度下梁端扣件受力、钢轨最大弯曲应力、轨道板稳定系数的变化情况，5种工况下最大扣件受力、钢轨弯曲应力和轨道板稳定系数如图13～15所示。

图13 不同坡度扣件最大受力Fig.13 Maximum stressof fastenerw ith differentslope

由图13和图14可知，在不同的桥梁温度跨度下，桥梁梁端处扣件最大拉力、最大压力、钢轨弯曲应力和轨道板最小稳定系数随着梁体纵向坡度的变化发生改变。在不同的桥梁梁体温度跨度下，桥梁梁端增设过渡板后梁端附近扣件最大压力与最大拉力均随着桥梁坡度的增加而线性增加，扣件最大压力略大于最大拉力，当梁体温度跨度为101m，桥梁坡度由5‰增大至35‰时，桥梁梁端处扣件最大拉力和最大压力均增大了近3.2倍。钢轨最大弯曲应力随着桥梁坡度线性变化，坡度越大，钢轨最大弯曲应力越大。

图14 不同坡度钢轨弯曲应力Fig.14 Bending stressof railw ith differentslope

由图15可知，轨道板稳定系数变化幅度在梁体纵向坡度为10‰时出现突变，在0‰～10‰范围内轨道板的稳定系数随着坡度的增加大幅度减小，在10‰～35‰范围内轨道板稳定系数也随着坡度的增加而减小，但变化幅度明显缓慢。在不同坡度情况下，轨道板稳定系数均大于安全限值1.3[18]。

图15 不同坡度轨道板稳定系数Fig.15 Stability coefficientof track slab w ith differentslope

综上所述，当桥梁位于温度变化幅度较大的地区时，为减小桥梁伸缩变形引起的梁端竖向位移和梁端扣件的受力，建议尽量减小桥梁梁体纵向坡度，确保梁端附近扣件的正常受力，保证轨道结构的稳定性。

4 结论

1)梁端轨道结构受力与桥梁温度跨度、梁体温差和梁体坡度呈正相关，随着温度跨度、梁体温差和纵向坡度的增大而增大，相反，轨道板稳定系数随着温度跨度、梁体温差和纵向坡度的增大而减小。

2)位于坡道上的桥梁，当梁体温度荷载为30℃时，梁端设置过渡板后最大弯曲应力减少了64.0%～64.9%，扣件最大拉力和最大压力分别减少了70.6%～76.8%和63.6%～74.3%；轨道板最小稳定系数增大了429%～769%。在大坡道桥梁梁端增设过渡板结构对于减小梁端轨道结构附加受力，增加轨道板稳定性起到了重要作用。

3)当桥梁温度跨度由88m增加至210m，桥梁纵向坡度为20‰时，扣件最大拉力和最大压力分别增大了2.4倍和2.5倍；钢轨弯曲应力大幅度增大；轨道板稳定系数变化幅度很小。

4)当桥梁坡度为0时，由于温度跨度引起桥梁纵向变形导致的梁端变形很小，梁端处扣件最大压力、最大拉力和钢轨弯曲应力均很小。当桥梁坡度由5‰增大至35‰，梁体温度跨度为101 m时，桥梁梁端处扣件最大拉力和最大压力均增大了近3.2倍。钢轨弯曲应力随着坡度增大而线性增大。