考虑坡面排水的公路超高缓和段坡度组合设计

张驰，向宇杰，林宣财，张昆仑，周郁茗

(1.长安大学 公路学院，陕西 西安 710064；2.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；3.广东省交通规划设计研究院集团股份有限公司，广东 广州 510627)

水是引起公路病害的主要原因，给行车安全造成隐患，高速公路线形设计中应保证路面排水通畅。由于超高缓和段的设置，高速公路易出现零度横向平坡，形成降雨积水点而引起安全行车隐患。潘兵宏等[1]研究表明，当道路纵坡较小时，渐变段综合坡度不能满足路表排水需求，易引发滑移导致重大安全事故。基于坡面排水对不同超高过渡段进行坡度组合设计可进一步提高坡面排水能力，保证行车安全。针对公路超高缓和段的设计和排水问题，国内外学者的相关研究主要集中在3个方面。一是对超高缓和段积水分布的模型构建。任俊雯等[2]基于运动波方程组描述了地表汇流过程，对地面粗糙系数和汇流长度径流系数等进行了敏感性分析；CRISTINA等[3]模拟了交通荷载下的城市路面降雨量的一维运动流模型；JEONG[4]应用扩散波模型，建模分析了不同条件下的路表积水情况；罗京等[5]对国内外几种典型路面水膜厚度预测模型进行验证和校核，通过降雨模拟实验标定了公路路面水膜厚度计算公式；RES‐SEL等[6]利用平均水深浅水方程建立了模拟路面径流二维模型；FWA等[7]通过Fluent流体力学建立模型，研究车辆滑水时的临界车速与积水深度和轮胎花纹深度的关系；祁颖智[8]通过建立路面径流过程仿真模型归纳总结平纵横线形要素、降雨强度和路侧排水方式等对路面径流行为的影响规律。二是对超高缓和段排水技术的研究。CHARBE‐NEAU等[9]通过在板面黏结不同级配粒料模拟不同条件下路面径流数据；戚明敏[10]通过对超高过渡段的几何特性和超高过渡段水流运动路径等变化特性的分析，提出了超高过渡段的排水改善方案；季天剑等[11]通过路面积水模拟实验，建立了路面积水厚度与路面构造深度和坡面等因素的多元回归模型及人工神经网络模型；杨洋等[12]基于汽车横向稳定性，从最大超高值、最大横向力系数、超高值与曲线半径分配、渐变率和渐变段设置5个方面对超高设计进行研究；张爱花等[13]针对已竣工工程中超高过渡排水不良路段，提出通过路面切槽构建微型截水沟提高路面排水能力。三是基于坡面排水的超高缓和段设计研究。潘兵宏等[14]根据公路设计中3种超高过渡起点设置方式，从超高过渡段的排水和车辆行驶舒适性方面对3种方式进行对比分析；刘琦[15]针对上下坡情况，讨论了纵坡、超高渐变率与排水不良路段长度的关系，为超高渐变率设计提出参考；张卓等[16]以力学为基础，建立了超高缓和段流水路径长度与纵坡之间的关系模型；周万虎等[17]分析了超高过渡段设计中超高渐变率和道路纵坡、合成坡度和路面排水的关系；张燕飞[18]研究了超高过渡段路面积水和降雨强度、公路路线线形和超高过渡方式的关系，提出了降雨条件下高速公路交通安全保障技术；王祎祚等[19]采用模拟降雨实验，获得水泥混凝土路表水膜厚度回归方程，表明相同条件下水泥混凝土表水膜厚度值高于沥青路面。综上可知，在超高缓和段排水设计的研究中，多是以缓和段为对象，进行模型构建分析影响因素的正向研究。而相应的逆向研究较为缺乏，即基于不同影响因素及其相互作用，构建相应的积水分布模型，进行实验设计得出适宜的超高缓和段的几何设计。本文综合考虑超高缓和段的坡度组合设计，为研究不同缓和段的最佳坡度组合设计，通过引入流体力学中的圣维南方程和曼宁公式，利用有限元方法对道路网格单元间的径流传递特征和径流深度进行分析，构建超高缓和段积水深度分布模型。并以道路纵坡、超高横坡和降雨强度为变量，基于超高缓和段长度或超高渐变率设计实验对最佳坡度组合进行分析。

1 基于有限元超高缓和段积水深度分布模型构建

圣维南方程在洪水演算、排水设计等诸多二维浅水流动的研究中应用广泛，且基于扩散波模型的圣维南方程用于模拟复杂路面上雨水流动时误差较小[20]，曼宁公式在明渠道流量或流速计算时过程较为简单，且在水力学中应用广泛。鉴于此，本研究综合圣维南方程和曼宁公式构建超高缓和段的积水深度分布模型。

考虑到超高缓和段的排水路径不均匀以及侧向压力梯度的影响，忽略惯性项即构成曼宁公式的扩散波模型，如式(1)：

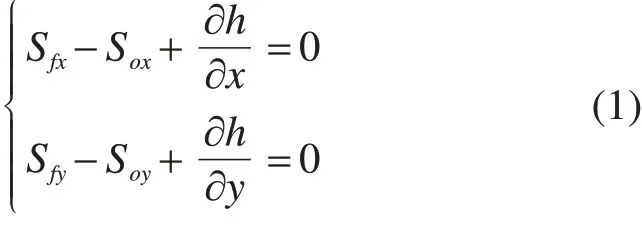
式中：Sfx和Sfy为沿x和y方向的摩擦项，反映路面径流内部及边界的摩阻损失；Sox和Soy为沿x和y方向的重力项，反映坡底变化引起的重力作用；∂h/∂x和∂h/∂y为沿x和y方向的压力项，反映径流深度的影响。

研究过程中，主要考虑径流深度和流量，对曼宁公式进行单位体积转化，得到矢量形式表示如式(2)：

其中：h为流动深度；n为曼宁系数(本研究中取值0.015)；Sf是合成坡度。可以推导出曼宁公式非线性扩散系数是关于水深、曼宁系数和摩擦斜率的函数，则曼宁公式的扩散系数表达式如式(3)：

扩散系数是表示给定条件下流动的扩散系数的标量值。如果水的自由表面是局部平坦，即合成坡度为0，水不会流动，Dh为无穷大。但在实际计算中，坡度为0时，扩散系数Dh记为0。

对道路模型进行简化后，划分道路网格，并提取网格单元边界的高程、纵坡和横坡。使用三点中心差分和Crank-Nicolson法对道路网格间的径流传递进行计算，如图1所示为道路网格中第(i,j)网格，Q为网格间的流量传递，ξ和η分别为道路纵坡方向和横坡方向，相应的Δξ和Δη为网格的长度和宽度。

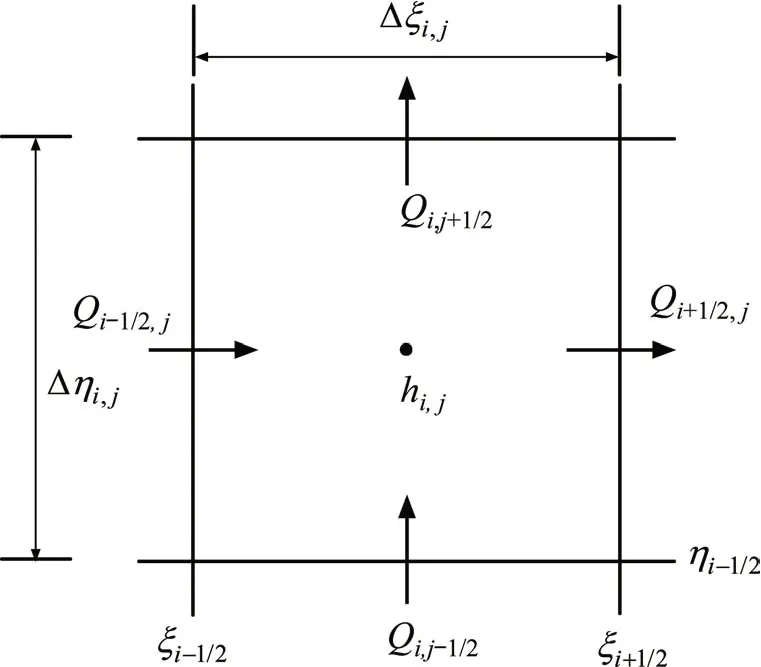
图1 网格(i，j)的流量流向Fig.1 Flow direction of grid(i,j)

记网格的面积为Ai,j，将上述网格间的流量代入圣维南连续性方程中，可得式(4)：

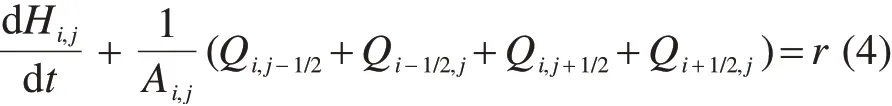
式中：Hi,j为道路网格单元中的水头高度，为主要变量，m；Ai,j为网格单元区域的面积，m2；Q为网格单元向外排除或向内流入的流量，m3；r为恒定的降雨密度，mm/h。

在道路网格中，主要变量H以网格单元为单位计算，而流量Q则在网格单元边界处计算。由三点差分中心法，可得网格单元右边界的扩散系数表达式如式(5)，其他边界的扩散系数同理可得。

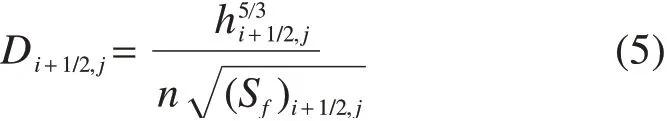
与网格单元(i，j)相关联的纵向和横向流量离散化如式(6)：

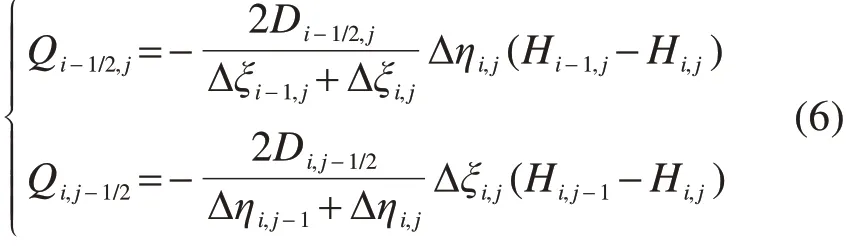
式中：Q为网格单元的流量传递，m3；D为扩散系数；H为水头高度，m；Δξ和Δη为网格单元的长度和宽度，单位：m或mm。

在道路网格系统中，若以流量Q作为网格间的径流传递单位，则需控制网格体积一致，但在实际操作中，道路网格的划分往往难以实现控制网格等体积。为了参数化网格间水流传递，引入在空间和时间上变化的传递系数C，定义为相邻网格间单位时间内传递的流量与该2个网格所构成区域面积的比值。利用曼宁公式的非线性扩散系数的计算公式，得到网格间传递系数的计算式如式(7)：

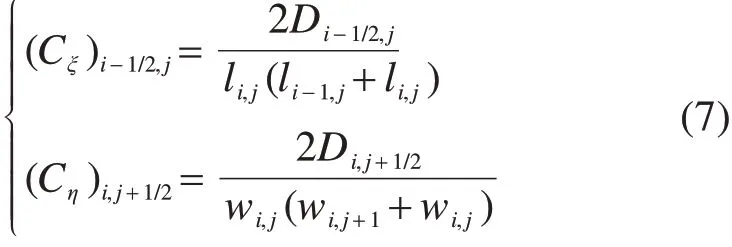
式中：Cξ为网格沿道路纵向的扩散系数；Cη为网格沿道路横向的扩散系数；li,j和wi,j为网格单元的长度和宽度，m。

采用内插值方法计算边界中心处的径流深度和有效非线性扩散系数。流体力学中，径流的流速表示为水深的函数，同时也受到坡度的影响，即道路高程变化的影响。考虑以上2类因素，结合式(5)～(6)和曼宁公式的非线性扩散波模型，并代入连续性方程简化后得式(8)：

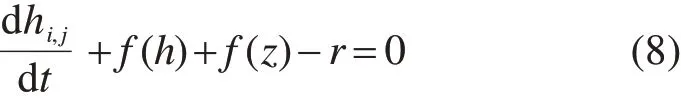
其中：f(h)和f(z)分别是考虑径流深度和高程对流速的影响而进行的修正。在实际应用中，水面高度(H)通常比水深(h)大几个数量级。因此，水深项用作减少截断误差的主要变量，截断误差由水深和表面高度之间的差异(h/z=10-6)引起。利用Crank-Nicolson方法得出时间阶段性的径流水深的迭代方程组如式(9)：

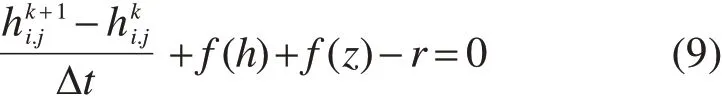
为减少其他环境因素的干扰，假定降雨开始前，道路路面干燥，即初始路表径流水深为hi,j=0。通过模拟道路倾斜表面确定上游端和下游端的边界条件。为控制得出不同坡度组合对积水深度的影响，现阶段将道路超高缓和段视为封闭的区域，直缓端边界网格单元间的传递仅考虑沿道路纵向和横向的流量流出，不考虑区域外流量的流入，缓圆端边界网格单元间的传递仅考虑沿道路纵向和横向方向的流量流入，不考虑区域内网格单元流量的流出。本研究中，将公路超高缓和段的径流形态视作宽浅明渠水流汇集的过程，因此，路边界汇集的水流仅能沿道路纵向流动。

2 模型验证

考虑到道路网格划分的难易程度，可根据道路超高缓和段的实际长度和宽度情况进行网格划分，如图2所示。

图2 超高缓和段网格划分Fig.2 Meshing of superelevation transition section

基于式(9)进行程序设计，流程图如图3所示。设置时间梯度，实现基于时间梯度公路路表的径流深度的迭代计算。

图3 模型程序设计流程图Fig.3 Modelprogram design flow chart

根据计算获取该超高缓和段在假定降雨强度下连续时间梯度的路表径流深度矩阵。随着时间梯度的推移，路表径流深度会趋近某个稳定状态。实验对各个时间梯度的路表积水深度分布状况绘制等高线图，并对所绘制的积水深度分布图进行对比分析，可知一定时间梯度后超高缓和段的水深分布不再发生变化，可认为积水深度分布趋近于稳定。

为对模型的可行性进行验证，不考虑模型生成边缘单元的积水分布。以双向4车道整体式路基公路的单侧为例，超高过渡方式为绕中央分隔带边线旋转。在路拱横坡ig=2%的状态下分别控制纵坡i，超高横坡ih和降雨量r进行实验，具体结果如图4所示。

对图4进行分析可知：1)纵坡由2%增至3%或超高横坡由2%增至3%时，道路积水较浅部分的面积增大，深水区域向横坡较低处缩聚，且水深稍有增加，水深最大值前者为7mm，后者为12mm。纵坡与横坡对径流深度的变化影响较大，但横坡更为显著；其次，随坡度的增加，径流长度变短。2)降雨强度由1mm/m in增至1.2mm/m in时，积水分布状态基本一致，深度有所增加。降雨强度的增大能够显著地使路表积水流速的分布发生变化，随着降雨强度的增大，路表积水流速变大，降雨能够更快地流动。3)若径流长度较长，如图4(a)和图4(d)，缓和坡面积水较深，面积较大，且排水相对较慢；增加横坡或纵坡后，如图4(b)和4(c)所示，径流长度变短，流速变大，排水加快。

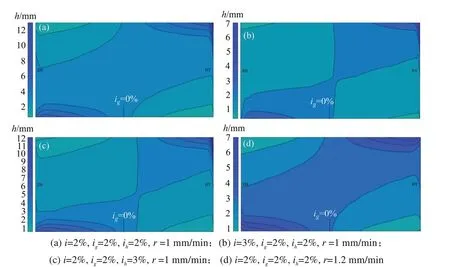
图4 不同条件下的积水深度分布Fig.4 Distributionmap of stagnantwaterdepth under differentconditions

祁颖智[8]在各要素对路面径流深度敏感性研究中，通过仿真分析得出降雨强度越大，路面径流深度越大；路拱横坡的增大有利于路面径流深度的减少，相较于纵坡，横坡的增加对于路面积水的快速排出效果更为显著。张理等[21]在研究路面坡度对水膜厚度的影响时，通过理论推导得出水膜厚度随着横坡坡度的增大而减小，随着纵坡的增大而增大，水膜厚度随着横坡减小而增大的幅度要明显大于水膜厚度随纵坡减小而减小的幅度。

综上可知，本研究所建立的模型能够较好地反映坡面径流问题。

3 实验设计

一般来说，纵坡越大越利于排水，在附加坡度的研究中，若纵坡大于1%，则不会因道路外侧抬起而形成坡度少于0.3%的纵坡。道路曲线段的超高值越大越利于坡面排水，但是不利于行车安全，一般地区的道路在设计中曲线超高值取值多为整数，如2%，3%，4%和5%，小半径曲线则会取较大值。纵坡或横坡较大，进行实验意义不大。为简化实验，本研究设定缓和段的超高渐变率为1/330，固定道路宽度，将道路纵坡、超高横坡和超高缓和段长度作为控制变量。道路纵坡坡度控制在0.3%～1%范围内，取值为0.3%，0.5%，0.7%和0.9%；超高横坡常规取值2%，3%，4%和5%，在此基础上进行坡度组合设计实验。

为研究得到在最利于坡面排水的坡度组合，按上述实验进行设计，评价得出纵坡临界值。在评价指标选取方面，需要考虑到在不同坡度组合下坡面积水的流速和径流在最不利位置的水膜厚度，以分别反映径流汇聚并流出路表的速度和对行车安全的影响。故以坡面径流流速和超高零坡处的积水厚度为评价指标。

3.1 径流流速

设定道路宽度为10m，路段长度为120m，提取道路网格，利用积水分布模型计算坡面各单元的径流深度。以道路横向为研究方向，计算网格单元间径流流速。各道路纵坡下的径流横向流速图如图5。

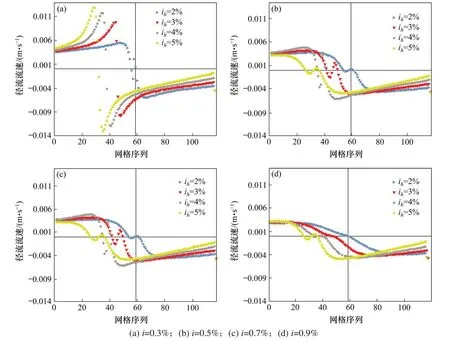
图5 不同纵坡下网格单元横向径流流速Fig.5 Transverse runoff velocity diagramsof grid cellsunder different longitudinalslopes

由图5易知，道路网格单元横向径流速度整体关于超高零坡呈对称分布，流速基本由两侧向超高零坡逐渐降低。分析可知：1)在实验的纵坡范围内，随坡度的增大横向径流流速的变化趋势愈加稳定，纵坡大于0.5%后，各网格单元间流速变化较小，保持稳定；2)在超高零坡(即各曲线与横轴的交点)及其附近区域，流速基本为0，在距离零坡约20m处，横向径流速度达到最高值；3)在同一纵坡条件下，超高横坡越大，其稳定横向径流速度越大，对比图5(a)和图5(b)，易知坡度增大，横向径流速度降幅愈大；4)对比纵坡0.5%，0.7%和0.9%时的径流流速，可以初步确定，纵坡0.3%～0.5%为宜，横坡排水能力优于纵坡。

各超高横坡下的径流横向流速如图6。

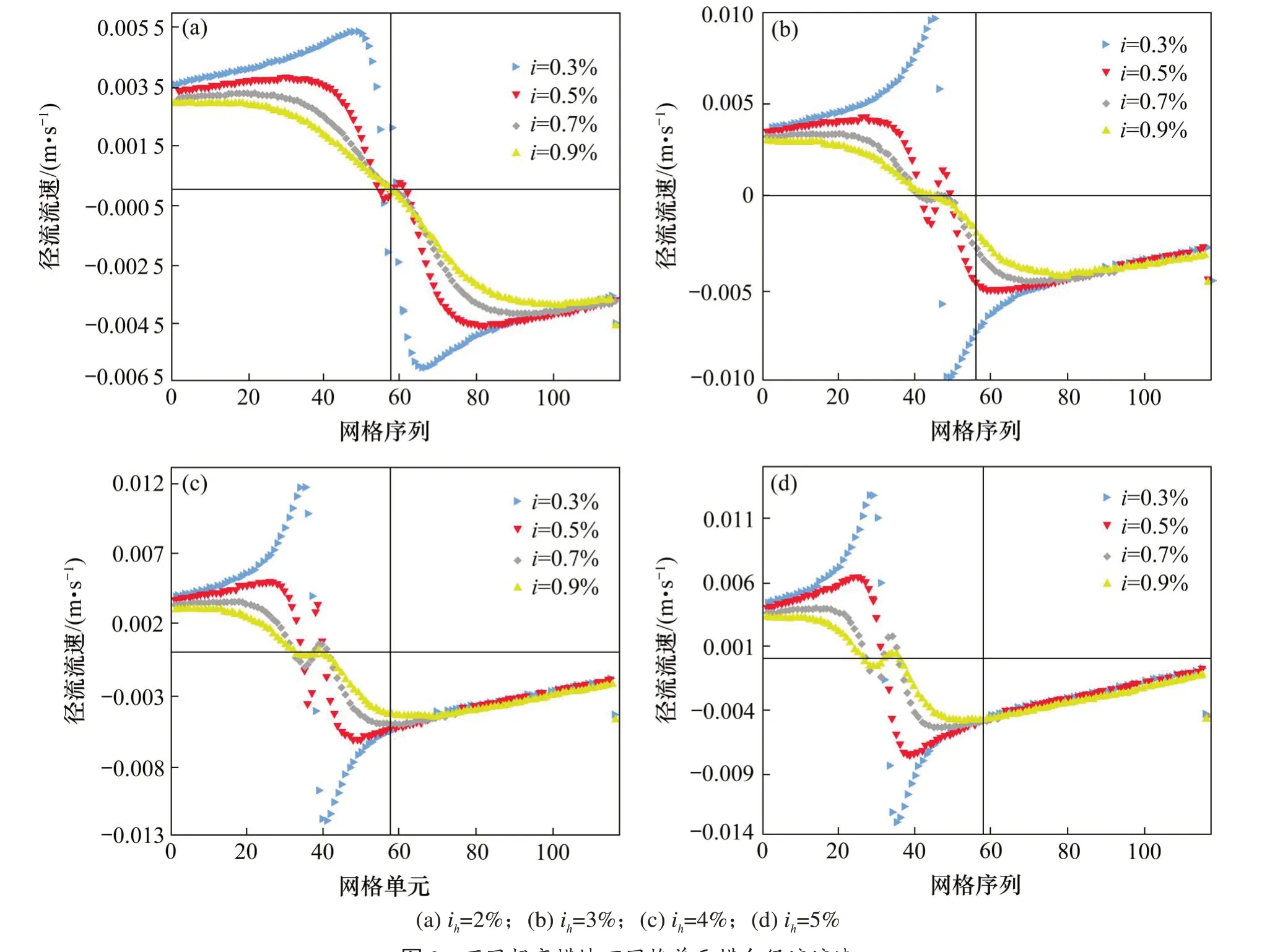
图6 不同超高横坡下网格单元横向径流流速Fig.6 Transverse runoff velocity diagramsof grid cellsunder differentsuperelevation cross slopes

不同超高值条件下，流速最大值分别为5.5，10，12和13mm/s，显然，超高横坡值的增大明显导致坡面流速的增大，且超高值在达4%后，径流速度趋于稳定。较图6相比，控制横坡不变时，不同纵坡间网格单元流速差距均小于控制纵坡时不同横坡间网格单元流速差距，可进一步验证道路横坡的坡面排水能力优于纵坡。初步可以确定，超高值取2%～4%间为宜。

3.2 径流深度

坡面积水深度对行车安全影响较大，为进一步研究超高缓和段的最佳坡度组合，需对超高零坡处的积水深度进行评价分析。计算获取各超高零坡处的径流深度值，具体如表1所示。

表1 不同坡度组合下超高零坡处积水深度均值Table 1 Average depth ofwateraccumulation at superelevation zero slope under differentslope combinations

根据表1可知，在一定的超高下，纵坡小于1%时，其坡面径流在超高横坡为0附近区域的积水深度变化较小，均约在5mm，变化幅度约为-0.1～0.1mm。易知，超高零坡附近区域的积水深度受纵坡和横坡影响均较小。在对横向径流流速研究时，初步确定适宜坡度为0.3%～0.5%，超高横坡适宜值为2%～4%。结合径流深度值的分析，纵坡临界值以0.3%～0.5%为宜，超高横坡值范围为2%～4%。

4 结语

1)在引入了水力学中的圣维南方程和曼宁公式的基础上，基于有限元对道路几何模型简化、提取并进行网格划分，对网格单元进行流动分析，考虑径流速度和道路高程对径流深度的影响，建立道路超高缓和段的积水深度分布模型，客观地反映实际的坡面水流状况。

2)实例分析验证了道路纵坡、横坡及降雨强度对路表积水径流深度有一定程度的影响。较道路纵坡相比，横坡对坡面排水的影响更为显著。在一般暴雨条件下，雨水主要集中在道路边界处，其位置靠近直缓端(缓圆端)，因此在确定道路泄水孔位置时，可根据边界积水深度分布进行判断。在道路设计阶段，在控制纵坡的基础上，为利于排水可适当增大超高横坡。

3)超高缓和段因附加坡度的存在易造成较小的合成坡度，等距选取纵坡范围0.3%～1%内的纵坡值进行差异性分析。实验验证了在一般暴雨条件下横坡对道路坡面排水的影响更显著，以道路网格单元横向径流流速和超高零坡附近的径流深度为评价指标，表明道路纵坡为0.3%～0.5%，超高横坡值为2%～4%时对超高缓和段道路的排水有利。

4)本研究在假设封闭区域情况下分析坡度组合对坡面排水的影响，后续的研究可将边界的流入和流出纳入进行分析。本实验调整纵坡与横坡，得出不同超高横坡下的临界纵坡值，但对纵坡值的研究范围缺乏一定的广度，在后期的研究将进行进一步的考虑。