重载交通纵坡路面结构受力分析及病害预估模型

宋宗强，马震宇，周 宁，陈小兵，于 雷，沈 凯，金 玮

（1.昆山市交通工程集团有限公司，江苏 苏州 215300；2.东南大学 交通学院，江苏 南京 210096；3.昆山交通发展控股集团有限公司，江苏 苏州 215300；4.德州市公安局交警支队交通设施管理维护大队，山东 德州 253000）

引言

目前，我国公路运输呈现出交通量大幅度增长、重载货车和超载车辆急剧增多的趋势，实际路面受力情况远超设计理论考虑情况，导致路面功能与结构的早期破坏多有发生［1-3］。在温度较高时，重载作用与高温条件发生耦合效应，从而加剧沥青面层的病害［4］。纵坡路段由于其受力状况的复杂性，在重载下易产生破坏。车辆行驶在纵坡上时，不仅在路面结构上施加了垂向荷载，还会施加切向荷载给路面结构。与平坡路段相比，纵坡段沥青路面会发生更严重的车辙等病害，主要原因是路面结构抵抗切向荷载的抗剪能力不足［5-7］。纵坡路段路面结构的力学响应计算可以有效地揭示纵坡路面的力学行为特征和破坏机理。纵坡段路面在轴载作用下的面层最大剪应力和竖向应变均大于平坡路段，且随荷载与坡度变化的增长速度也更快，中上面层则是病害产生最为严重的层位［8-9］。

针对沥青路面疲劳开裂与永久变形等破坏，已有相应的预估模型及计算公式，但未考虑纵坡对路面破坏产生的影响［10-11］。因此，研究重载交通作用下纵坡路段路面各结构层的受力情况，进而对路面病害预估模型进行纵坡修正，具有较好的实用价值。

1 有限元计算模型

1.1 路面结构与材料

选用典型的半刚性基层沥青路面结构，结构组成和材料物理参数见表1。

表1 路面结构与材料参数

1.2 荷载条件

车轮荷载施加位置为路面结构模型中部。由于车轮接地形状的实测结果接近矩形，路面结构有限元分析采用图1 的矩形荷载。荷载作用实际压强分布与面积见表2。

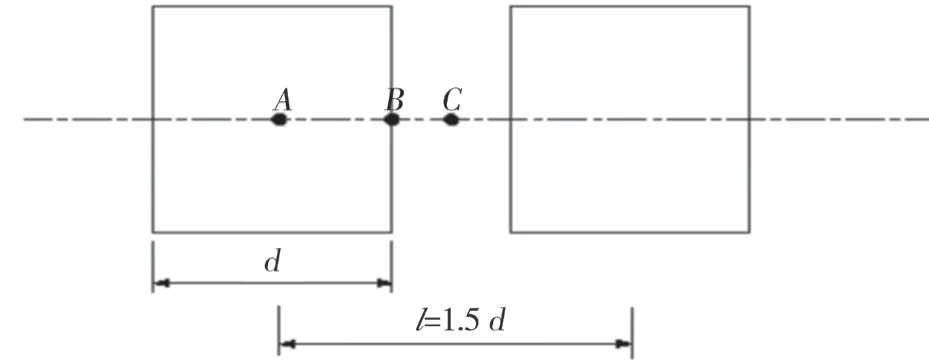
图1 荷载作用

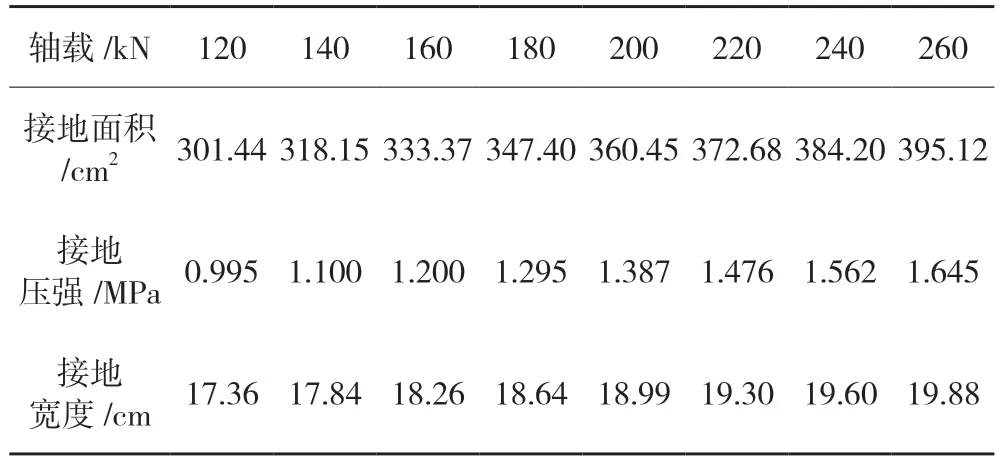
表2 各种轴载轮胎实测接地压强与面积

路面结构除受到垂向荷载外，还受到纵坡引起的切向荷载。根据力学分析，纵坡路段荷载作用见图2。

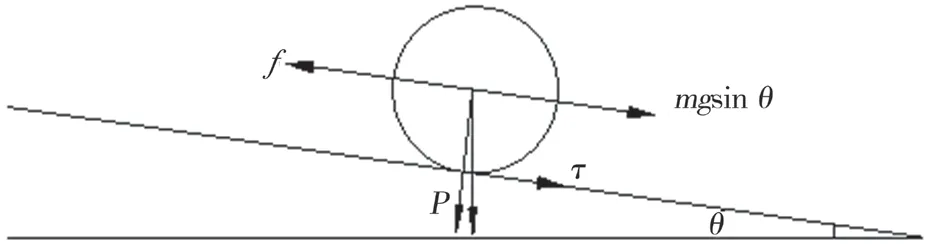
图2 纵坡路段荷载作用

图2 中：m—货车的总重量，kg；g—重力加速度，10 N/kg；θ—纵坡坡角，（°）；p—垂向荷载，MPa；τ—纵向切向荷载，MPa；坡度i=tanθ。当纵坡较小时，垂向荷载大小随着坡度的增加变化很小，将其定为常数。车辆在纵坡上行驶时，路面对驱动轴作用与行车方向一致的摩擦力f，为mgsinθ，此时路面承受切向荷载：

式中：S—车辆驱动轴单轮轮胎接地面积，m2。

公路超限检测站规定了六轴货车的标准总重不超过60 t，标准轴载应取100 kN。当货车总重取60 t时，在不同纵坡下对路面产生的纵向切向荷载计算结果见表3。

表3 纵坡上非超载货车所引起荷载

以超载50%的载重货车作为路面荷载，模拟计算超载作用下路面结构的受力情况。此时货车总重为90 t，由实测轴载谱分析，超载车辆的轴载取140 kN，车轮的接地压强取1.1 MPa。表4 为超载车辆对路面施加的荷载计算结果。

表4 纵坡上超载货车所引起荷载

1.3 有限元模型

有限单元模型把整体结构划分成有限个小单元，并将各单元利用结点相连结。除去边界上的固定结点，有限元法对各结点通过平衡条件求解其位移，从而获得各单元的内力［12］。

采用有限元模拟软件ABAQUS/Standard 对纵坡上的沥青路面结构静力响应进行分析［13］。路面模型尺寸X、Z 向取6 m，Y 向取真实路面厚度，土基厚取3 m。边界条件设置为底面在Y 方向上的位移为零，前后两面在Z 方向上的位移为零，左右两面在X 方向上的位移为零。模型中X 为垂直于行车方向（横向），Z 为行车方向（纵向），Y 为垂直于路面方向（竖向）。采用8 节点六面体线性缩减积分单元（C3D8R）划分网格，建立模型与网格划分见图3。

图3 路面结构模型

2 力学响应计算结果与分析

2.1 纵坡对路面结构剪应力影响分析

计算不同纵坡、不同负载状态下的路面纵向和横向剪应力，结果见图4、图5。

图4 纵坡对纵向、横向剪应力的影响

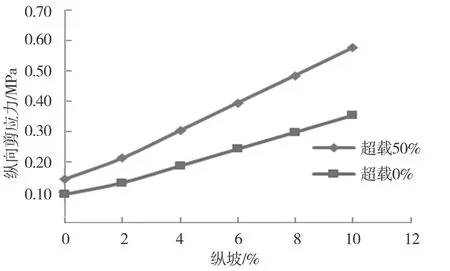
图5 超载对路面纵向剪应力的影响

由图4 可知，纵向剪应力数值随着纵坡增大而快速增加，横向剪应力数值则受纵坡变化的影响很小。因此，纵向剪应力可能是导致纵坡路段沥青路面出现推移、拥包等破坏的主要因素［14-16］。由图5可知，超载50%时路面纵向剪应力远超标准荷载状态，且两者的差值随纵坡增大而显著增大。当纵坡为4%至10%时，超载50%状态的路面纵向剪应力可达非超载状态的1.5 至2 倍。

图6 反映了超载作用下路面所受纵向剪应力的横向分布，其中虚线为荷载施加区域。图7 反映了超载作用下路面所受纵向剪应力沿深度的变化。

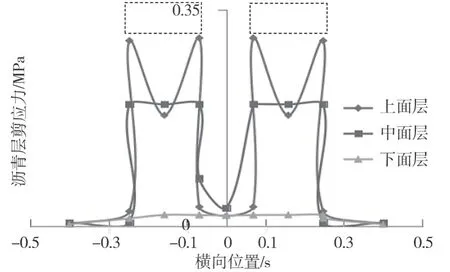
图6 重载作用下纵向剪应力横向变化

图7 重载作用下纵向剪应力沿深度变化

由图6 可知，上面层与中面层所受的纵向剪应力数值远大于下面层，且在荷载作用边界处有突变。在荷载作用区域，上面层与中面层的剪应力从轮载边缘向轮载中心处递减。下面层承受剪应力则具有数值小且横向分布均匀的特点。图7 结果表明，纵向剪应力主要分布在顶部10 m 深度内。随着深度增加，轮载边缘的剪应力急剧减小，轮载中心处的剪应力先增大后减小。当深度＞10 m 时，纵向剪应力可以忽略不计。

2.2 纵坡对沥青层最大拉应力和拉应变影响分析

计算不同纵坡、不同负载状态下沥青上面层的拉应力与拉应变变化趋势，结果见图8、图9。

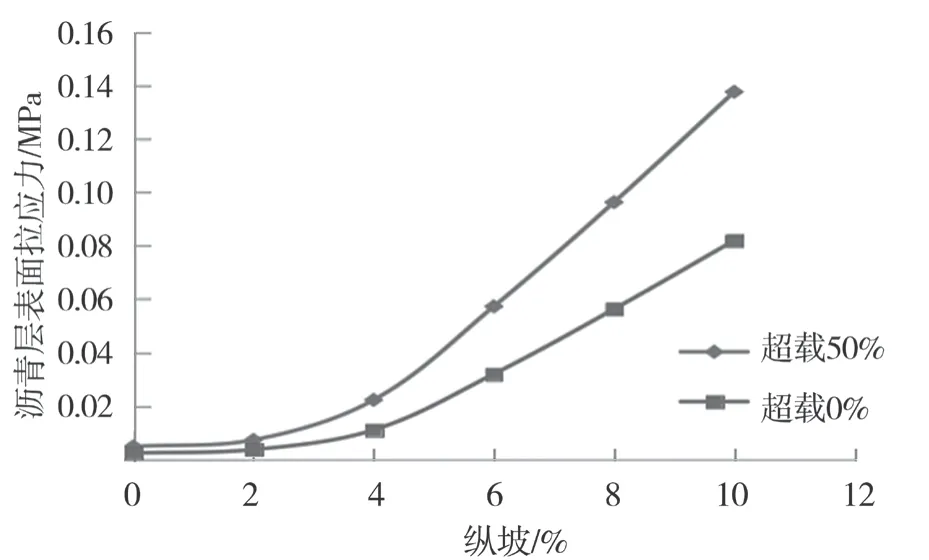
图8 纵坡和超载对沥青层拉应力的影响

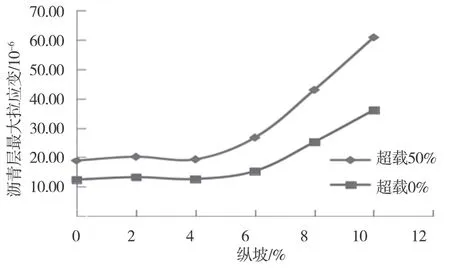
图9 纵坡和超载对沥青层拉应变的影响

由图8 可知，随着纵坡的增大，沥青层表面拉应力也不断增大，且在纵坡＞4%时增长趋势更加显著。相较于非超载状态，超载50%时的沥青层表面拉应力明显升高，且增长速度更快。由图9 可知，沥青层最大拉应变在纵坡超过4%后开始显著上升。相较于非超载状态，超载50%时拉应变数值有明显增加，可达非超载时的1.5 至2 倍。

3 纵坡路段路面病害预估模型修正

3.1 沥青层疲劳开裂预估模型

通常将沥青面层疲劳寿命量化为沥青路面设计期内累计标准轴载作用次数。已有研究对27 种不同沥青混合料进行108 次四点弯曲疲劳试验，得到沥青混合料疲劳模型［17］：

式中：Nf—沥青混合料疲劳寿命，次；ε—反复应变水平，10-6；S0—初始弯曲劲度模量，MPa；VFA—沥青混合料空隙率，%；A，b，c，d—回归系数。

《公路沥青路面设计规范》（JTG D50—2017）利用30 个试验路段的沥青路面疲劳试验数据对室内综合疲劳模型进行验证和修正，提出沥青层疲劳寿命预估模型［10］：

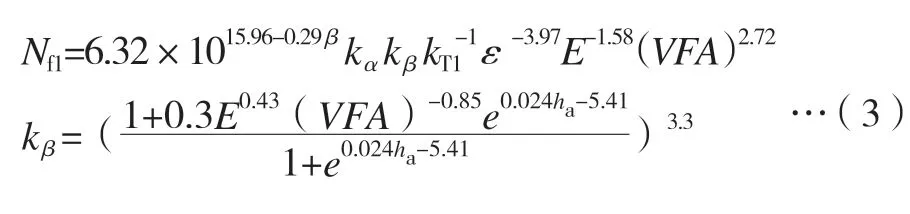
式中：Nf1—沥青层预估疲劳寿命，次；ha—沥青层层厚，mm；β—可靠度指标；kT1—温度调整系数；ε—标准荷载作用时沥青层层底拉应变，10-6；E—20 ℃、10 Hz 作用条件下沥青混合料动态压缩模量，MPa；VFA—混合料的沥青饱和度，%。

将公式（3）中与路面结构和材料相关的参数和常数合成为A，得到简化公式（4）。该公式忽略了纵坡对路面结构受力产生的影响。沥青层的拉应变随纵坡增大而增大，疲劳寿命则应相应减小。因此，引入纵坡修正系数以保证纵坡路段的模型可靠性，见公式（5）。纵坡修正系数见公式（6）。

式中：A—与路面结构相关的常数；Bi—纵坡修正系数；εi—标准轴载作用下纵坡为i 的路段沥青层层底拉应变。

通过回归得到纵坡坡度和修正系数的关系公式（7）。修正系数Bi的计算结果见表5。

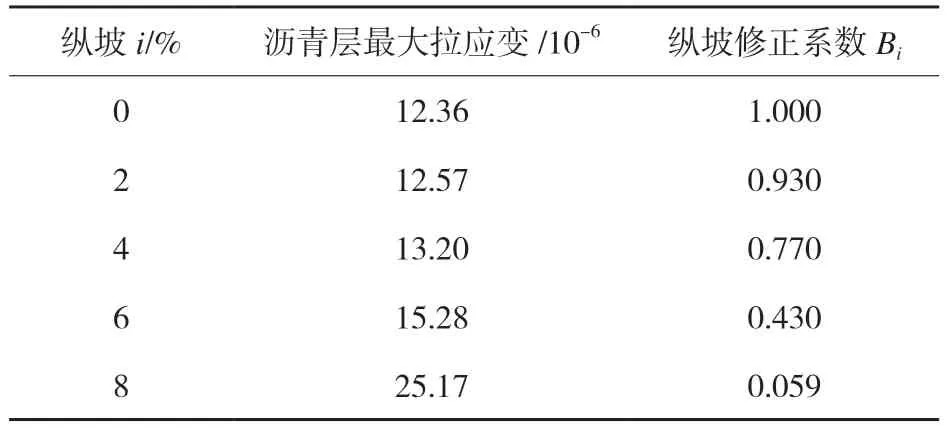
表5 疲劳模型在各纵坡的纵坡修正系数

3.2 沥青层永久变形计算模型

纵坡路段上车辙的计算除了考虑沥青层顶压应力外，还应该关注剪应力的作用。经大量车辙试验，得到沥青层永久变形与在考虑剪应力时的计算公式［11］。

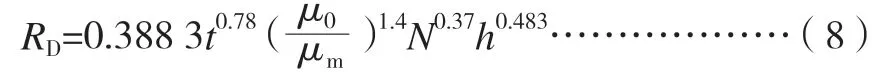
式中：RD—沥青层永久变形量，mm；t—沥青路面温度，℃；μ0—沥青路面在行车荷载作用下最大剪应力，MPa；μm—沥青混合料抗剪强度，MPa；N—标准轴载作用次数，次；h—沥青层厚度，m。

该模型没有反映出剪应力随纵坡的变化关系，纵坡路段上路面所受的剪应力和产生的变形量都应明显增大，因此，对模型进行纵坡修正。纵坡修正系数见公式（9），计算结果见表6。

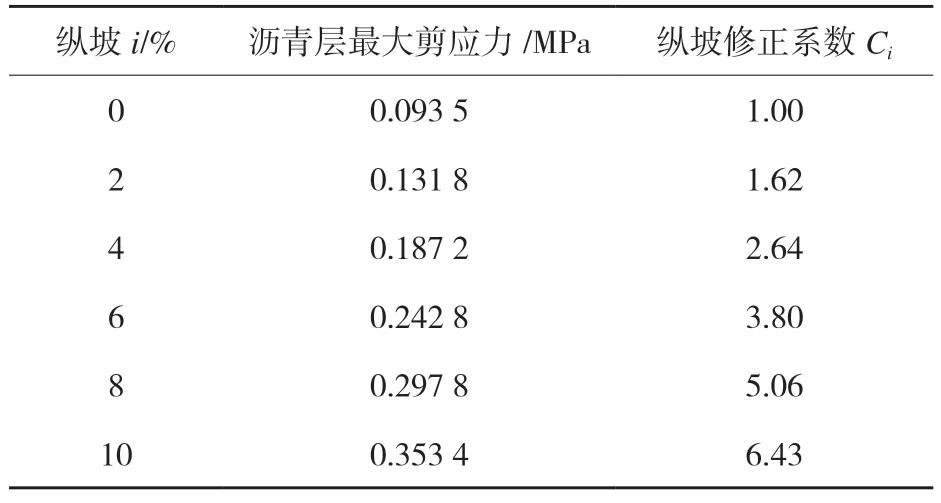
表6 永久变形模型在各纵坡的纵坡修正系数

式中：Ci—纵坡修正系数；μi—纵坡为i 的路段沥青路面在行车荷载作用下最大剪应力，MPa。

采用回归法处理表6 中的数据，求得纵坡修正系数Ci的表达式（10）。计算纵坡路段上沥青层的永久变形，可采用公式（11）的修正模型。

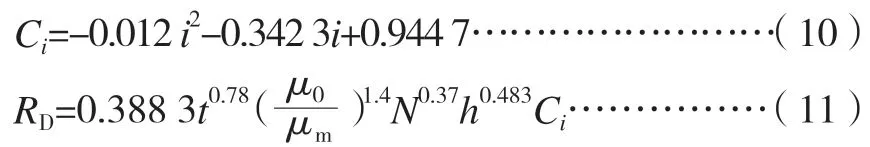
4 结语

（1）随着纵坡坡度的增大以及重载的作用，沥青路面结构纵向剪应力的数值显著上升。（2）超载作用下，纵坡沥青路面结构的上面层和中面层所受纵向剪应力与下面层相比更大，且在荷载施加的边缘处有突变现象。各结构层所承受的剪应力数值存在较大差异，在路面施工与使用过程中应注意保证层间连接不受破坏。（3）沥青层表面拉应力和拉应变随着纵坡的增加呈递增趋势，超载对拉应力和拉应变的大小也有明显的提高作用。（4）通过回归分析得到沥青层疲劳开裂纵坡修正系数Bi和沥青层永久变形纵坡修正系数Ci与纵坡坡度的关系，解决了原有模型没有考虑纵坡影响的问题，增大了其适用的普遍性，并且保证了修正后路面病害预估模型的可靠性。