水平循环荷载下斜坡段基桩动力响应特性模型试验研究

2022-09-23赵明华黄万江杨超炜彭文哲

铁道科学与工程学报 2022年8期

赵明华，黄万江，杨超炜，彭文哲

(湖南大学土木工程学院，湖南长沙 410082)

一般而言，高速公(铁)路桥梁上部结构传递给基桩的车辆制动荷载、风荷载及地震荷载等均可视为水平循环荷载。此外，受山区水文地质条件、道路选线及环境保护等方面的限制，在高速公(铁)路桥梁工程修建过程中，难免会将基桩架设在斜坡上，导致此类基桩的动力响应特性相当复杂[1-2]。目前，国内外较多学者均已关注并开展了斜坡段基桩响应特性的相关研究。已有学者在充分分析斜坡段基桩响应特性的基础上，建立了静荷载下斜坡段基桩的简化力学模型，并提出了可考虑复杂影响因素的斜坡段基桩内力与位移计算方法[3-4]。相比理论分析，数值模拟可以更加精细地控制边界条件。GEORGIADIS等[5-6]采用数值软件探讨了各种因素对斜坡段基桩响应特性的影响。赵明华等[7]采用现场试验对斜坡段基桩进行了研究。EL等[8-10]采用模型试验探讨了各因素对斜坡段基桩的桩顶水平位移和桩身弯矩的影响。但是部分学者在对模型试验进行设计时未考虑与工程原型之间的相似关系，所得出的结论虽然具有一定的参考意义，但是与实际工程的关系较弱[11]。上述研究主要采取各种方法对静荷载作用下斜坡段基桩的响应特性进行了研究，而考虑到车辆制动荷载等循环荷载对斜坡段基桩的作用较为频繁，且循环荷载与静荷载的性质差别较大，故有必要考虑循环荷载对基桩响应特性的影响。现有关于水平循环荷载研究的对象多为平地基桩，且多采用模型试验进行研究，如陈仁朋等[12]在饱和粉土地基中开展了基桩水平循环加载试验；王海新等[13]通过模型试验探究了循环荷载幅值和频率等因素对桩身应变和桩身轴力等的影响；张勋等[14]设计长期水平循环加载模型试验，探讨了砂土地基中单桩累积变形与长期水平循环荷载之间的关系。也有部分学者，如GIANNAKOS等[15]引入砂土循环本构关系建立三维有限元模型，分析了3种不同类型的循环荷载对基桩动力响应特性的影响；汪优等[16]建立超长桩的数值模型，探讨了循环荷载的频率和荷载幅值等因素对超长桩动力特性的影响。以上研究均认识到了平地基桩在水平循环荷载下的响应特性与在静荷载下的响应特性具有较大差别，但斜坡段基桩的受力特性与平地基桩相比也存在较大差异，导致上述研究成果难以直接应用于水平循环荷载下斜坡段基桩的设计。综上，已有学者对静荷载下的斜坡段基桩与水平循环荷载下的平地基桩进行了深入研究，但是综合二者的水平循环荷载下斜坡段基桩动力响应特性的研究目前鲜有报道，因此有必要对其展开深入研究。本文拟开展考虑相似关系的室内模型试验，探究斜坡坡度、水平荷载幅值及循环次数等因素对斜坡段基桩动力响应特性的影响，以期为同类工程的设计与施工提供参考。

1 模型试验设计

1.1 模型边坡和模型桩

模型试验以张(家界)—花(垣)高速公路泗溪河一桥某基桩为工程原型[7]。该基桩为典型的斜坡段嵌岩桩，桩位处斜坡坡度为40°～60°，桩身材料为C25混凝土，直径d为2.0m，桩长l为25m。模型桩选用外径为32mm，壁厚为4.4mm的三型聚丙烯管(PPR管)，入土深度为1 m，嵌固深度为50mm。模型边坡采用河砂填筑，通过室内土工试验可测得其各项物理力学参数为：重度γ=18.83 kN/m3，含水率ω=3.84%，压缩模量Es,1-2=4.43 MPa，比重Gs=2.62，孔隙比e=0.42，内摩擦角φ=13.80°，表观黏聚力c=7.84 kPa，曲率系数Cc=0.94，不均匀系数Cu=5.74。

1.2 模型箱

模型箱长宽高分别为1.6，1.0和2.2m，两侧面为透明玻璃，其他面为高强度钢板，四周由型钢进行固定。填筑斜坡时始终保证模型桩埋置深度为1.0m，则模型桩设置及试验加载如图1所示。模型桩与模型箱箱壁之间的最小间距约为15dm，足以消除试验过程之中边界效应的影响[17]。

图1 模型试验Fig.1 M odel test

1.3 相似关系

根据相似理论可知，若模型试验能够表现出与工程原型相似的物理现象，则二者的物理力学参数之间应具有一定的比例关系，如式(1)所示[18]。工程原型与模型试验的物理力学参数如表1所示。

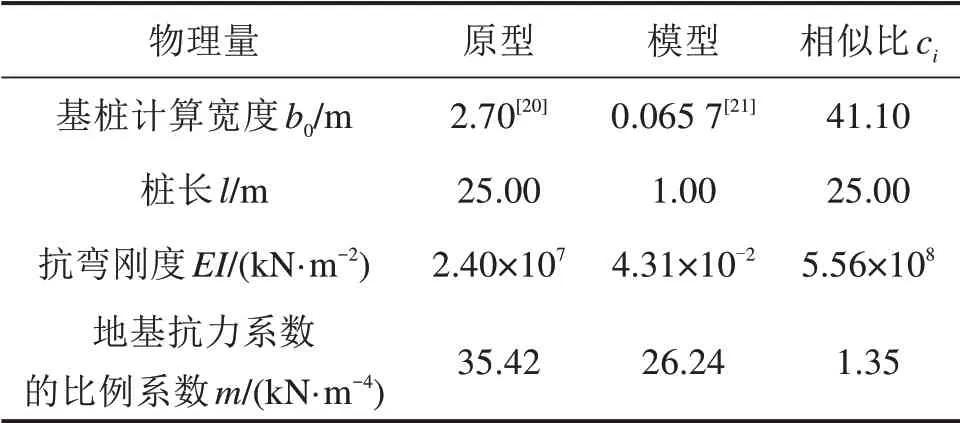
表1 工程原型与模型试验物理力学参数Table 1 Physicalandmechanicalparameter table of engineering prototype andmodel test

式中：ci为物理力学参数i的相似比；ip为工程原型的某物理力学参数；im为模型试验的对应物理力学参数。

工程原型斜坡段基桩的弹性挠曲微分方程如式(2)所示[19]。

式中：w为基桩桩身挠度，m；z为桩身某点距地表的距离，m，且cz=cl；P为竖向荷载，N。

利用工程原型与模型试验中各物理力学参数之间的相似关系，可得式(3)。

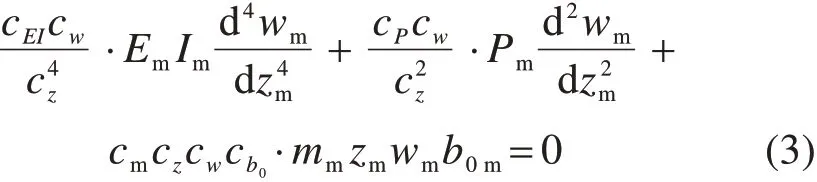
由相似理论可知，若要使式(3)成立，需满足式(4)所示条件。

依据式(4)可得本模型试验的相似指标κ1和κ2，如式(5)和式(6)所示。将表1中的相似比代入，可得κ1=0.97。根据文献[7]中工程原型基桩的情况，并结合已有数据及令κ2=1.00，可得应施加在模型桩上的竖向荷载Pm=80N。

1.4 试验方案

根据J2试验结果(H为20，30和40 N时，xJ的实测数据分别为1.99，3.70和5.64 mm)，并结合《公路桥涵地基与基础设计规范》中桩顶最大水平位移为6mm的规定[20]，且考虑到多通道协调加载试验系统的加载精度(所加荷载越小，越容易出现较大波动)，取M 1，M 2和M 3试验的水平荷载幅值为30 N。考虑到本试验斜坡段基桩对水平荷载幅值的变化较为敏感，故取M 4和M 5试验的水平荷载幅值分别为20 N和40 N。为探究斜坡坡度、水平荷载幅值及循环次数等因素对斜坡段基桩动力响应特性的影响，制定如表2所示的试验方案。

表2 模型试验方案Table 2 Model testplan

1.5 加载设置

本试验采用圆筒状铁块在桩顶施加竖向荷载，并以多通道协调加载试验系统施加水平荷载。当水平荷载采用循环加载模式时，由于试验条件限制及为分析方便起见，一个周期内的荷载波形如图2所示，其中加载阶段、保持阶段及卸载阶段的持续时间均为10 s。

图2 水平循环荷载波形Fig.2 Lateral cyclic load waveform

1.6 数据采集

试验中采用的测试元件：DMWY-100型位移计(量程为100 mm)，BFH120-5AA-D150型应变片，具体布置如图3所示。

图3 桩身测试元件布置Fig.3 Layoutof pile testcomponents

利用实测桩身应变并结合式(7)，可得桩身各截面的弯矩值。

式中：M为桩身弯矩，N∙m；εy和εl为桩身测点的压应变和拉应变。

J1和J2试验1m in采集一次试验数据，当桩顶水平位移xJ大于30mm时，停止加载。M 1，M 2，M 3，M 4和M 5试验1 s采集一次试验数据，当水平荷载循环加载次数n=2 500次时，停止试验。

2 试验结果与分析

2.1 斜坡坡度

由图4可知，随着加载进程的继续，桩顶水平位移的增长速度逐渐减小，但考虑到临空面的存在，其增长速度将不会降为0，即随着循环次数增加，桩顶水平位移将持续增大。由于本研究中竖向荷载较大，随着循环加载进程的继续，桩顶水平位移受P-Δ效应的影响逐渐变大，且在加载循环中桩顶水平位移的变化规律与水平循环荷载的波形相对应。从图5可知，当循环次数增量Δn=100时，M 1，M 2和M 3试验每一加载周期内最大桩顶水平位移的变化速率Δx1/Δn分别由0.125降到0.002，0.169降到0.003，0.257降到0.006。可知当n<100时，桩顶水平位移的变化较为剧烈，而n>100时，桩顶水平位移的增大速度逐渐降低，故可认为n<100时，斜坡段基桩的动力响应特性对循环次数的变化较为敏感。此外，当n>100时，桩顶水平位移上、下包络线之间的差值不随着水平荷载循环次数的增加而发生变化，M 1，M 2和M 3试验桩顶水平位移上、下包络线的差值分别保持在0.72，1.95和2.92mm左右，表明斜坡坡度与水平受荷桩的承载稳定性呈负相关关系。

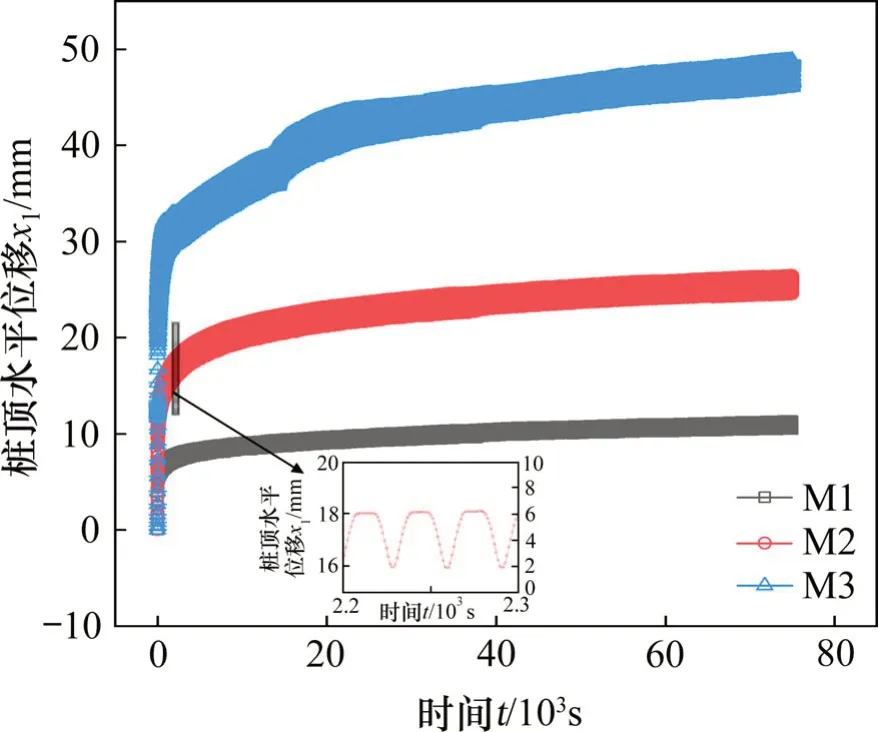
图4 不同斜坡坡度下时程位移曲线Fig.4 Time history displacementcurvesunder different slope inclinations

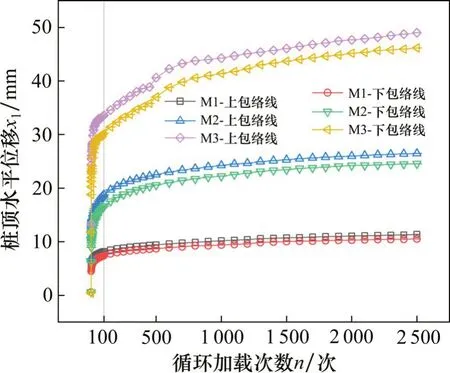
图5 不同斜坡坡度下桩顶水平位移与循环次数的关系Fig.5 Relationship between pile top horizontal displacement and cycle timesunder differentslope inclinations

由于加载周期内桩顶水平位移的最大值一般出现在tT=20 s时，故取tT=20 s时的桩身弯矩进行分析。由图6可知，M 1，M 2和M 3试验中桩身弯矩最大值分别约为4.04，6.88和8.84N∙m，大致出现在3～4dm，6～7dm和9～10dm深度范围内，表明随着斜坡坡度增加，临空面浅层地基土体所能提供的极限抗力逐渐减小，导致桩身弯矩最大值及其所处深度逐渐增大。此外，桩身反弯点逐渐下移，表明桩身发生正弯曲的长度逐渐增大。

图6 不同斜坡坡度下桩身弯矩分布(n=100,t T=20 s)Fig.6 Bendingmomentof the pile under differentslope inclinations(n=100,t T=20 s)

2.2 水平荷载幅值

从图7可知，在循环加载进程中，桩顶水平位移及其变化速率与水平循环荷载幅值均成正比。在J2试验中，当水平静荷载H=20，30和40 N时，对应的桩顶水平位移xJ分别为1.99，3.70和5.64mm。M 2，M 4和M 5试验每一加载周期内最大桩顶水平位移与对应静荷载桩顶水平位移之比x1/xJ的数值范围分别为2.57～10.08，2.47～8.09，2.66～10.22。从图8可知，随着水平荷载幅值的增大，循环荷载与静荷载相比，其对基桩的承载性能提出了更高的要求。从图9可知，当斜坡坡度为45°时，桩身弯矩最大值出现在6～7dm深度范围内，且随着荷载幅值的增大，桩身弯矩最大值所处位置有逐渐下移的趋势。M 2，M 4和M 5试验的桩身弯矩最大值分别约为6.88，3.77和10.47N∙m，与M 4试验相比，M 2和M 5试验桩身弯矩最大值分别增加了82.49%和177.72%，表明桩身弯矩最大值随水平荷载幅值增加呈非线性增大的趋势。

图7 不同水平荷载幅值下时程位移曲线Fig.7 Time history displacementcurvesunder different lateral load amplitudes

图8 不同水平荷载幅值下桩顶水平位移与循环次数的关系Fig.8 Relationship betw een pile top horizontal displacement and cycle timesunder different lateral load amplitudes

图9 不同水平荷载幅值下桩身弯矩分布(n=100，t T=20 s)Fig.9 Bendingmomentof the pile under different lateral load amplitudes(n=100，t T=20 s)

2.3 循环次数

图10～12为不同斜坡坡度下各循环次数(n=1，100，600，1200，1 800和2 400)的桩身弯矩分布。可知，在不同斜坡坡度下，随着循环次数增加，桩身反弯点逐渐下移，表明桩前地基抗力的作用范围逐渐变大。桩身弯矩随循环次数不断增大在一定程度上表明了桩前土体会在循环加载进程中逐渐弱化，且基桩的承载力也将逐渐降低。M 1，M 2和M 3试验中不同循环次数下桩身弯矩变化较大的范围z/l分别为0.40，0.55和0.64，斜坡坡度越大，桩身弯矩随循环次数增加而出现显著增大的深度范围越大，即桩前土体的弱化范围越大。桩前土体弱化将导致基桩承载力降低，故基桩承载性能与斜坡坡度及循环次数均呈负相关关系。从图10～12可推出，当n<100时，基桩承载力降低速度较快，如在循环加载初期发生桩顶水平位移过大或增长过快等问题，应尽早处治。

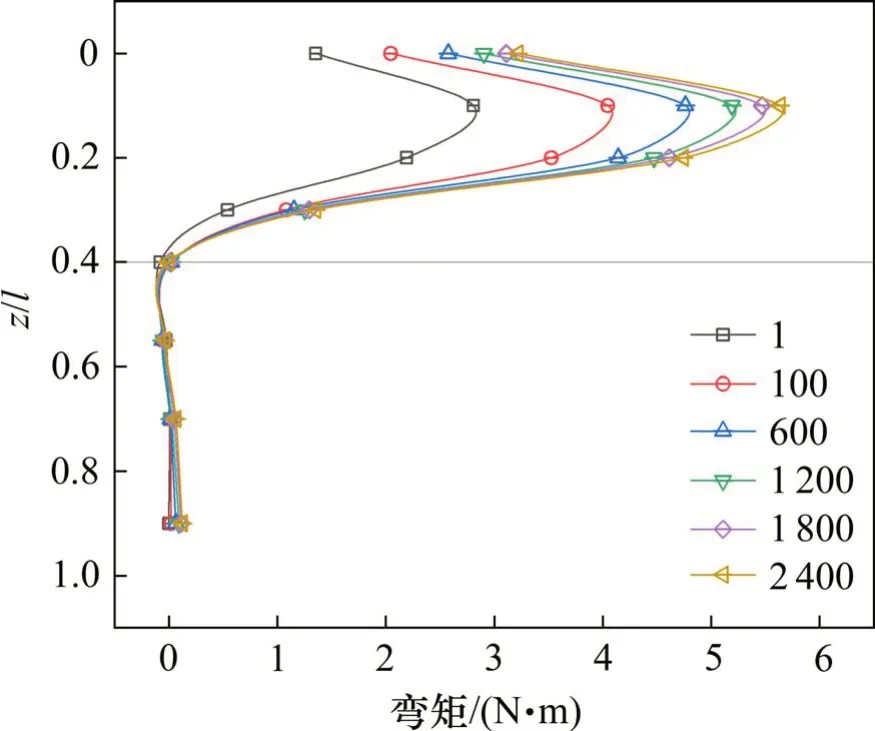
图10 M 1试验-不同水平荷载循环次数下桩身弯矩分布(t T=20 s)Fig.10 M 1 test-bendingmomentof the pile under different lateral load cyclic numbers(t T=20 s)

图11 M 2试验-不同水平荷载循环次数下桩身弯矩分布(t T=20 s)Fig.11 M 2 test-bendingmomentof the pile under different lateral load cyclic numbers(t T=20 s)

3 水平循环荷载下斜坡段基桩桩顶水平位移计算

通过试验结果可知，水平循环荷载下斜坡段基桩桩顶水平位移的影响因素较多，而相应的理论计算方法似未见报道。鉴于此，本文基于水平静荷载下桩顶水平位移，提出循环荷载下斜坡段基桩桩顶水平位移的计算方法。

借助有限元软件M idasGTSNX对J2试验进行模拟，其中模型桩为圆筒形，外径为32mm，壁厚为4.4mm，埋深为1.0m，弹性模量为1.16 GPa，则相应的抗弯刚度为43.10N∙m。斜坡土体采用摩尔-库伦模型，具体物理力学参数参见1.1小节，模型桩与斜坡土体均采用四面体实体单元进行离散。模型桩与斜坡土体之间的接触关系采用库伦摩擦界面单元来进行模拟，通过对J2试验进行模拟，可反算出其法向刚度模量取为630 kPa，切向刚度模量取为100 kPa。采用数值模拟计算所得桩顶水平位移与J2试验实测数据如图13所示，二者吻合较好，相对误差控制在10%以内，满足精度要求，表明该数值模型具有较高的可靠性。

图13 J2验实测桩顶水平位移与数值模拟结果对比Fig.13 Comparisonsofmeasured horizontaldisplacementof pile top in test J2 and numerical results

在拟合精度满足要求的基础上，利用M idas GTSNX对不同斜坡坡度(30°和60°)工况进行模拟，可得各静荷载工况下的桩顶水平位移xJ，如表3所示。

图12 M 3试验-不同水平荷载循环次数下桩身弯矩分布(t T=20 s)Fig.12 M 3 test-bendingmomentof the pile underdifferent lateral load cyclic numbers(t T=20 s)

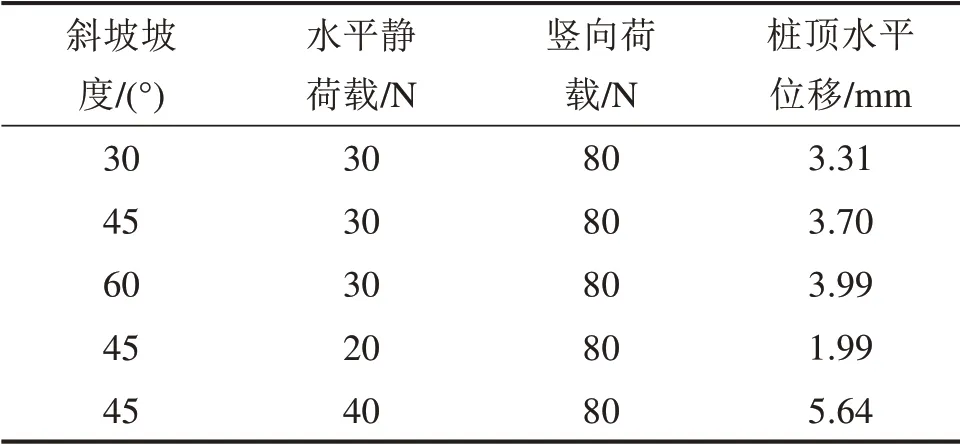
表3 静荷载下桩顶水平位移-x JTable 3 Horizontaldisplacementof pile top under static loads-x J

由图4和图6可知，不同循环次数下的最大桩顶水平位移x1与循环次数n近似呈幂函数关系。鉴于此，通过对比试算，可采用式(8)和式(9)来表示循环荷载下桩顶水平位移x1与对应静荷载下桩顶水平位移xJ及循环次数n之间的关系。

式中：f为循环效应系数；K，a和b为与斜坡坡度及水平荷载幅值有关的系数，可通过模型试验实测数据进行拟合得到。

通过拟合可知，a为不随斜坡坡度及水平荷载幅值变化的常数(a=0.11)，K和b与斜坡坡度及水平荷载幅值的关系分别如式(10)和式(11)所示。

式中：θ为斜坡坡度，(°)；HA为水平循环荷载幅值，kN。

拟合公式计算出的桩顶水平位移与模型试验的实测数据对比如图14和图15所示，显然，二者吻合较好，相对误差在10%以内，满足精度要求。依据试验设计可知，拟合公式(8)～(11)适用于斜坡坡度为30°～60°，桩顶有较大竖向荷载且水平循环荷载幅值HA小于静荷载条件下xJ=6mm时桩顶所能承受的水平荷载值，且上部为较为松散的土体，下部为承载力较好的完整岩体的嵌岩基桩的计算。

图14 不同斜坡坡度下拟合公式计算结果与实测结果对比Fig.14 Com parisonsbetween results calculated by fitting formula andmeasured resultsunderdifferentslope inclinations

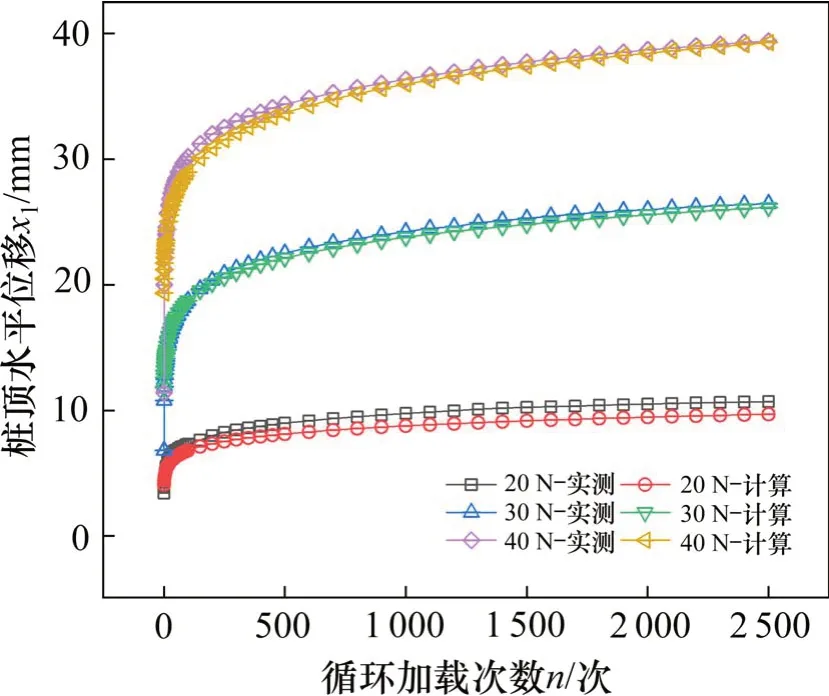
图15 不同荷载幅值下拟合公式计算结果与实测结果对比Fig.15 Comparisonsbetween results calculated by fitting formula andmeasured resultsunder different load amplitudes

该拟合公式借助循环效应系数f在不同循环次数下最大桩顶水平位移与相应静荷载下桩顶水平位移之间建立了联系，为计算水平循环荷载下桩顶水平位移提供了新思路和新方法。据此，可通过静荷载下桩顶水平位移，计算不同循环次数下最大桩顶水平位移，进而根据桩顶水平位移允许值确定循环荷载下的基桩水平承载力。显然，本文拟合公式可为水平循环荷载下斜坡段基桩的设计提供一定的借鉴和指导。