多对多越库配送绿色车辆路径问题及算法研究

2022-09-23周果季彬方晓平

铁道科学与工程学报 2022年8期

周果，季彬，方晓平

(中南大学交通运输工程学院，湖南长沙 410075)

近年来，物流业飞速发展，但物流配送产生的运输和仓储成本居高不下。为提高货物的运转效率、降低运输和仓储成本，越库配送模式应运而生，并成功应用于沃尔玛、Toyota等企业。该模式下，货物只在越库中心短时间停留中转，不进行仓储，以有效降低库存水平、提高库存周转率，适用于零售以及生鲜等需求稳定或时效性较高的产品[1-2]。越库配送车辆路径问题(Vehicle routing problem w ith cross-docking,VRPCD)由LEE等[3]首次提出。葛显龙等[4]以运输成本与车辆固定成本之和最小化为目标，建立了多越库中心VRPCD模型。崔巍等[5]考虑越库中心分拣能力，研究了带批次和临时库存的VRPCD，并提出混合变邻域搜索粒子群算法求解。上述研究均假设取货车辆协同到达越库中心，随后将货物分装送至客户点，并未考虑供应商与客户之间的供需匹配关系。WEN等[6]在VRPCD基础上考虑供应商与客户之间的供需匹配关系，提出了一对一VRPCD。假设每个供应商只为一个客户提供货物且每个客户只由一个供应商提供货物。随后，国内外学者针对上述一对一VRPCD提出了大量的启发式求解算法，如大邻域搜索算法[7]、改进的变邻域搜索算法[8]、基于列生成的两阶段算法[9]等。然而，在实际配送作业中，每个客户所需货物种类多样。例如，以超市、药店等为代表的企业通常所需货品种类繁多，而每个供应商通常只生产其中几种货品，并不能满足所有需求。在此背景下，NIKOLOPOULOU等[10]首次对多对多越库配送车辆路径问题(Many-tomany vehicle routing problem w ith cross-docking,MM VRPCD)进行研究，以运输距离最小化为目标建立了该问题的混合整数线性规划模型。相较于传统VRPCD，M-M VRPCD不仅需要考虑取送货路径优化，还需要考虑供应商与客户之间的供需匹配关系，问题求解难度更大。随着绿色、低碳理念的不断深入倡导，各方从产业结构和布局、管理和技术等不同层面大力推进节能减排。在物流配送领域，考虑油耗与碳排放的绿色车辆路径问题(Green vehicle routing problem,GVRP)也成为研究的一个热点。ERDOĞAN等[11]于2012年首次提出GVRP的概念。YU等[12]对考虑碳排放与时间窗的GVRP进行研究，并提出了分支定价算法求解该问题。周鲜成等[13]考虑时变速度和实时载重对车辆油耗和碳排放的影响，以确定车辆油耗和碳排放的度量函数，进而建立多车场GVRP模型。张得志等[14]以配送总成本最小、车队规模最小以及客户时间满意度最大为目标，建立基于低碳视角的多目标GVRP模型。综上，学者们对考虑不同优化目标的GVRP问题展开研究，拓展了其应用场景。但目前考虑油耗与碳排放等绿色节能因素的GVRP模型与算法不能直接应用于VRPCD的求解，而国内外针对多对多越库配送车辆路径问题的研究也未考虑油耗与碳排放等绿色节能因素。基于此，本文考虑碳排放与油耗因素，以车辆运营成本、碳排放成本以及油耗成本最小化为目标，建立了多对多的越库配送绿色车辆路径问题(Many-to-many green vehicle routing problem w ith cross-docking,M-M GVRPCD)模型。根据该问题供需关系耦合、离散组合方案多样的特征，设计了自适应大邻域搜索(Adaptive large neighborhood search,ALNS)算法，并进行大量数值仿真实验。

1 问题描述与模型构建

1.1 问题描述

本文研究了多对多越库配送绿色车辆路径问题，即物流配送网络中存在一个越库中心、若干供应商与客户，集货车辆将不同供应商的货物集中至越库中心，并在越库中心根据客户订单需求对货物进行整合，最后调度车辆将货物配送至相应的客户处。配送过程中，车辆的碳排放量以及油耗量与车辆的行驶状态(速度、载重等)相关。该问题的优化目标为：综合考虑车辆运营成本、碳排放成本以及油耗成本情况下，合理调度车辆进行取送货作业，使得总成本最小。

在多货品运输网络中，供应商能够提供不同品类货物，同样客户需求由不同供应商来满足。如图1(a)所示，供应商1为客户1',2',3'提供货物，客户1'需要供应商1和3为其匹配需求，故供应商1处供货量为q1=q11'+q12'+q13'，客户1'的需求量为q1'=q11'+q31'。图1(b)展示了该示例的配送路径示意图。此外，对问题做出如下合理假设：1)供应商、客户的供需匹配关系以及时间窗已知；2)取/送货车辆需要从越库中心出发，完成取/送货任务后必须返回越库中心；3)车辆在越库中心以及各节点的装卸货时间相同[15]。

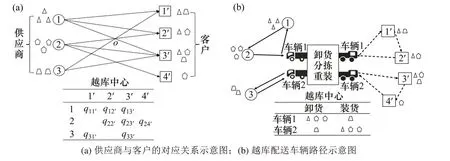
图1 多对多越库配送车辆路径问题示意图Fig.1 Schematic diagram of themany-to-many vehicle routing problem w ith cross-docking

1.2 模型构建

1.2.1 参数符号

将M-M GVRPCD定义为一个有向图G=(E,N)，N=S∪O∪D表示所有节点的集合，其中，S={1,2,…,n}和D={1',2',…,n'}分别代表供应商节点与客户节点的集合。O={o1,o2,o3,o4}代表越库中心，其中为取货路径的起终点，o3,o4为送货路径的起终点。可行弧集合包含E1:{(i,j):i,j∊S∪{o1,o2},i≠j} 和E2:{(i,j):i,j∊D∪{o3,o4},i≠j}2个子集，其中，cij(i,j∊N)为弧(i,j)的距离，tij(i,j∊N)为每条弧的旅行时间。

V：所有车辆的集合。

VS,VD：取货与送货车辆的集合。

QS,QD：取货与送货车辆的最大载重。

qi：节点i的货物重量。

f,g：车辆装货/卸货时间。

ET,LT：越库中心服务时间窗。

Hij：表示供应商i与客户j的供需匹配关系。当供应商i为客户j供货时Hij=1；否则，Hij=0。

Fc：单位距离运营成本，元/km。

Fa：单位油耗成本，元/L。

Fm：单位碳排放成本，元/kg。

M：一个大的常数。

变量：

：0-1变量，当车辆从i节点行驶到j节点时；否则

：0-1变量，当i节点被车辆v服务时否则，

：车辆v离开节点i的时间。

uv：取货车辆在越库中心的卸货完成时间。

lv：送货车辆开始装货的时间。

1.2.2 油耗与碳排放率计算

考虑到车辆实时载重对油耗影响，本文采用XIAO等[16]提出的基于载重的油耗模型(Load based fuel consumption model，LFCM)计算车辆油耗量。车辆v在弧(i,j)油耗率计算如下：

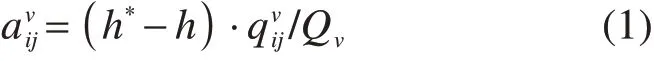
式中：h*为车辆满载时的油耗率，L/km，h为空载时的油耗率，L/km，h*与h取值分别设定为2和为车辆v在弧(i,j)段的载重，kg；Qv为车辆v的最大载重，kg。

碳排放测度模型中应用最广的为HICKMAN[17]提出的MEET模型，该模型碳排放估计函数如下：

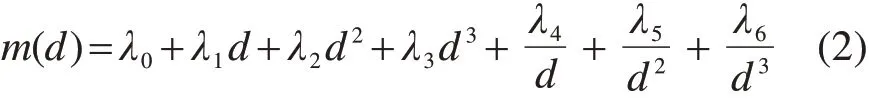
其中，m(d)表示车辆的碳排放率，kg/km，d为车辆平均速度，km/h，参数(λ0,λ1,λ2,λ3,λ4,λ5,λ6)取值与车辆属性相关。本文考虑到以超市、药店等为代表的企业，假设配送所用车辆为车辆重量小于3.5 t的货车，其碳排放率测度表达式如下[17]：

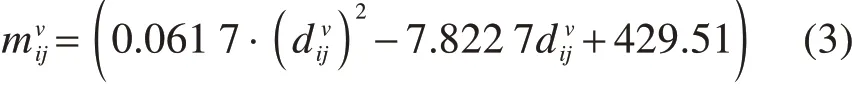
式中：表示车辆v在弧(i,j)段的行驶速度，km/h。

1.2.3 模型建立

假定Fc，Fa和Fm分别为单位距离运营成本(元/km)、单位距离油耗成本(元/L)、单位距离碳排放成本(元/kg)。考虑到车辆在运输途中产生的驾驶员薪酬、路桥费、保险费等，将这些费用统称为“车辆运营成本”。现有研究表明，运输途中的车辆运营成本可近似用行驶距离的线性函数表示[18]，故本文采用车辆行驶距离来计算车辆运营成本。车辆油耗成本和车辆碳排放成本分别由前文所述的LFCM和MEET模型进行计算。以车辆运营成本、碳排放成本以及油耗成本之和最小化为目标，构建M-M GVRPCD模型如下：

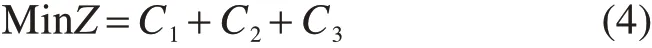
其中：

爸爸依然笃定地一步步向前走去，好像没有什么东西会让他回头……可是当他走到拐弯处，就在他侧身拐弯的刹那，好像不经意似的悄悄回过头来，很快地瞟了弟弟他们一眼，然后才消失在拐弯处。

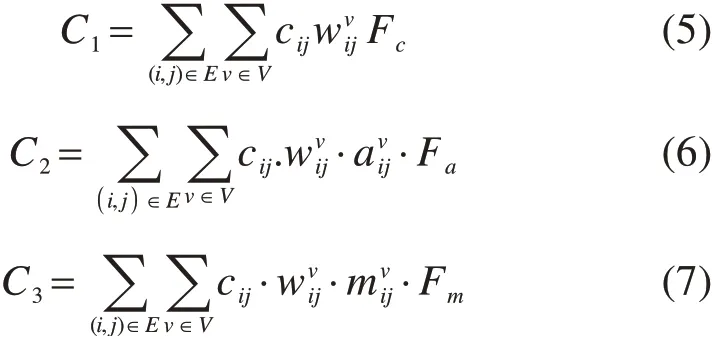
s.t.

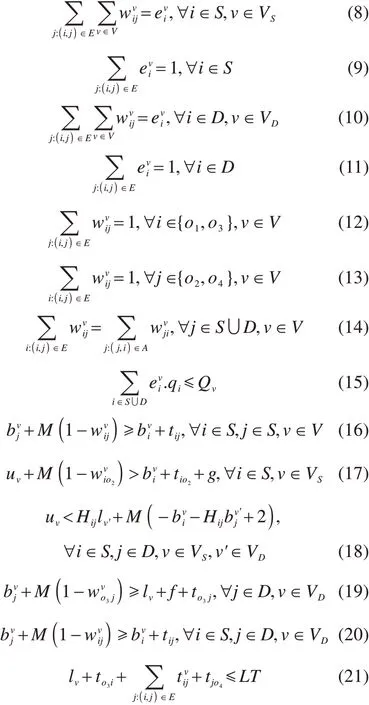
目标函数(4)表示配送总成本最小化，其中C1为车辆运营成本，C2为油耗成本，C3为碳排放成本。约束(8)和(9)表示每个供应商只能被一辆车服务，约束(10)和(11)表示每个客户只能同时被一辆车服务。约束(12)和(13)表示车辆从越库中心出发，最终回到越库中心。约束(14)表示流量守恒，约束(15)表示车辆装载的货物总重量不超过车辆最大载重。约束(16)表示节点i和j由同一车辆服务时，服务结束时间关系。约束(17)计算集货车辆到达越库中心并完成卸货的时间。约束(18)表示送货车辆必须等集货车辆完成卸货之后才开始装货。约束(19)计算送货车辆完成装货从越库中心出发的时间。约束(20)与约束(16)类似，计算送货过程中同一辆车服务的相邻节点服务结束时间关系。约束(21)表示越库中心的服务时间窗约束。

2 求解M-M GVRPCD的自适应大邻域搜索算法

多对多越库配送绿色车辆路径问题作为VRP的拓展，是NP难问题。相较于VRP，越库模式中取、送货路径之间存在复杂的耦合关系，且该问题需要考虑的约束条件更多、求解难度更大。同时，供应商与客户之间多对多的供需匹配关系使得问题离散组合方案巨大，传统的邻域搜索算法搜索空间有限，难以有效求解该问题。

自适应大邻域搜索算法(Adaptive large neigh‐borhood search，ALNS)是根据大邻域搜索算法的思想进一步拓展而来。较于其他邻域搜索算法，ALNS因其破坏、修复机制能够实现大邻域的构造，具有更强的全局搜索能力；同时，该算法框架需构造多个破坏和修复算子并进行自适应贪婪选择，使得算法具有更好的鲁棒性，针对不同特征的问题具有更强的适应性。鉴于ALNS算法求解各类VRP的高效表现，同时针对M-M GVRPCD供需关系、复杂耦合特征以及离散组合方案巨大的特点，本文采用ALNS算法框架并设计了移除算子和修复算子求解该问题，具体流程图如图2所示。

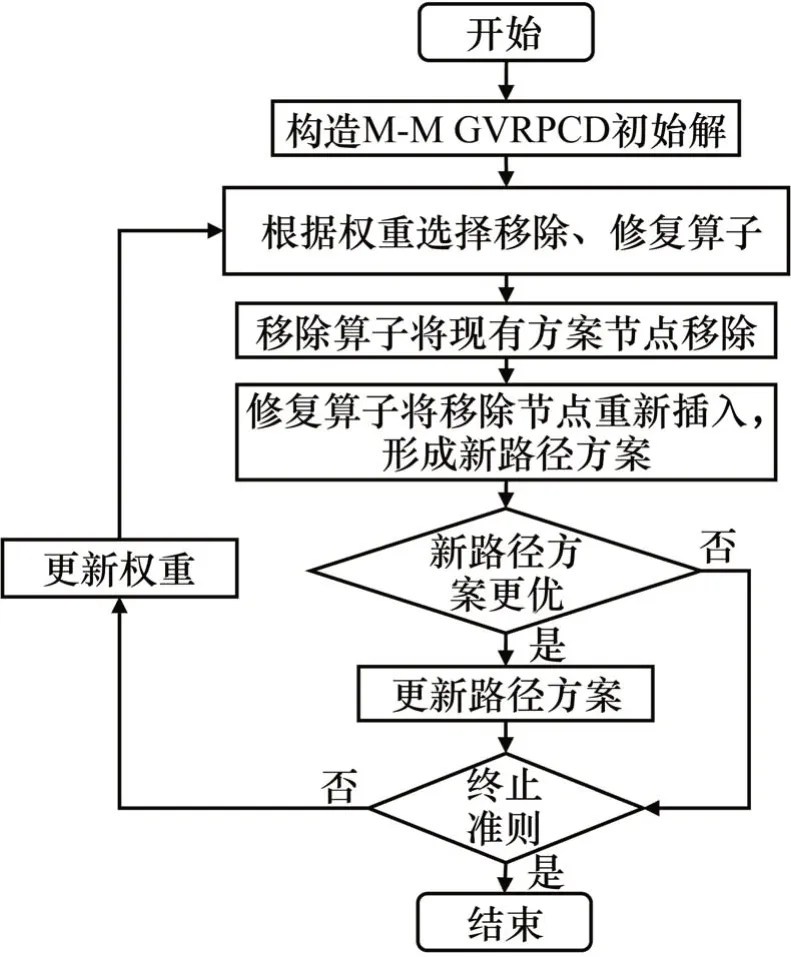
图2 算法框架示意图Fig.2 Schematic diagram of algorithm framework

2.1 构造初始解

本文基于节约算法[19]思想以快速构造初始解。具体步骤如下：首先为每个节点分配一辆空车，每次迭代过程中选择节约值最大的2条路径进行合并，直至合并任意2条路径不能达到节约里程目的时终止迭代。合并任意2条路径vi，vj的节约值定义为：Δcij=Ci+Cj-Cij，其中Ci，Cj表示路径vi，vj的总成本，Cij表示合并两路径之后的总成本。

2.2 移除算子

移除算子旨在通过一定方式从当前解结构中移除部分供应商或客户节点，其中移除数量ρ在[1,δ]中随机产生，δ为移除节点数上限。

最差移除算子：该算子每次都移除对当前解目标函数贡献最大的节点，旨在插入使总成本更小的位置[20]。具体移除过程可描述为：假设表示节点i从位置η处移除带来的目标函数值改变，则其中Ob(P)为当前解P的目标函数值，为将节点i从位置η处移除后的目标函数值。在移除过程中，遍历每个节点，优先移除值最大的节点。此外，每次移除过后需更新解结构。设定随机扰动参数γ，增加移除的多样性，避免陷入局部最优。随机移除算子：随机移除算子指每次从解中随机移除一定数量的供应商或客户节点，该算子通过引入随机性丰富搜索解过程的多样性。

2.3 修复算子

从当前解中移除ρ个节点后，通过修复算子将移除的节点重新插入到解结构中以构造新解。插入过程中需满足载重约束以及越库相关约束，否则将插入该节点后的目标函数增量设置为无穷大。每次插入一个节点后都需要更新解结构。若无可行插入位置，则增添一辆车。

深度贪婪修复算子：该算子通过遍历所有满足约束的可行位置，并选择使目标函数增量最小的最佳插入位置[20]。假设Ob(P-)为移除节点后的解结构P-的目标函数值，Ob(P-,i,η)表示节点i插入了位置η后解结构的目标函数值，则节点i插入了位置η的插入成本为插入过程中，首先遍历所有供应商与客户节点并记录每个节点的最佳插入位置以及最佳插入成本，继而选择最佳插入成本最小的节点优先插入。

随机修复算子：与随机移除算子类似，随机修复算子在所有满足约束位置中随机选择可行位置插入节点。

2.4 权重更新与解接受规则

迭代过程中，根据算子历史表现更新算子分数μ及使用次数π。若产生的新解优于最好解，μ增加σ1，若产生的新解优于当前解但劣于最好解，μ增加σ2；若接受的新解劣于当前解，μ增加σ3。算子i的权重θ的更新如下：

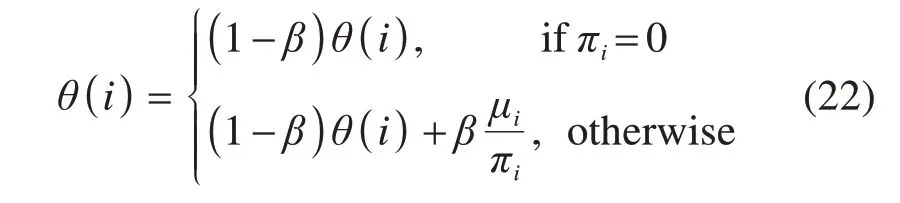
式中：β∊[0,1]是反应参数，该参数反映算子历史表现对于后续迭代的影响。

本文采用模拟退火新解接受准则，即若新解优于当前解，则接收新解为下一代的当前解，否则以exp(Ob(P)-Ob(P′))/Tc的概率接受新解，其中Tc为模拟退火当前温度。

3 结果分析

3.1 算例生成与参数

本文根据文献[6]提供的VRPCD算例，生成不同规模的算例，节点位置坐标值从算例200e中随机选取。算例中供应商节点数占总节点数的比值设定30%，40%，50%3种情形。同时，算例将每个供应商所能服务的最大客户数定义为供应商-客户供需比，并设定了2和3这2种情形。供应商为每个客户所提供的货物重量(qi)在[0,20]范围内随机生成。取货车辆最大载重为送货车辆最大载重QD=0.5QS。

模型中单位油耗、碳排放成本参数设置参考文献[13]中的设定，具体如表1。经过多次实验测试，ALNS算法参数值设置如表2。本文算法用Python 3.8编程实现，所有算例均运行10次。所有实验在配置为Intel Core i5-8500(3.00 GHz)，内存8G，操作系统为Windows10的机器上测试。

表1 模型参数设定Table 1 Parameter settingsofmodelalgorithm

表2 ALNS算法参数设定Table 2 Parameter settingsof the ALNSalgorithm

3.2 算例结果分析

3.2.1 路径方案分析

图3展示了算例20-2-0.4的车辆行驶路线图，图中实线表示取货路径、虚线表示送货路径。3辆取货车辆从越库中心出发将不同供应商处的货物集中至越库中心。随后，在越库中心根据客户订单对货物进行整合，调派2辆送货车辆将货物配送至相应客户处。通过越库中心的整合过程可以更好地优化取送货过程，减少总成本。

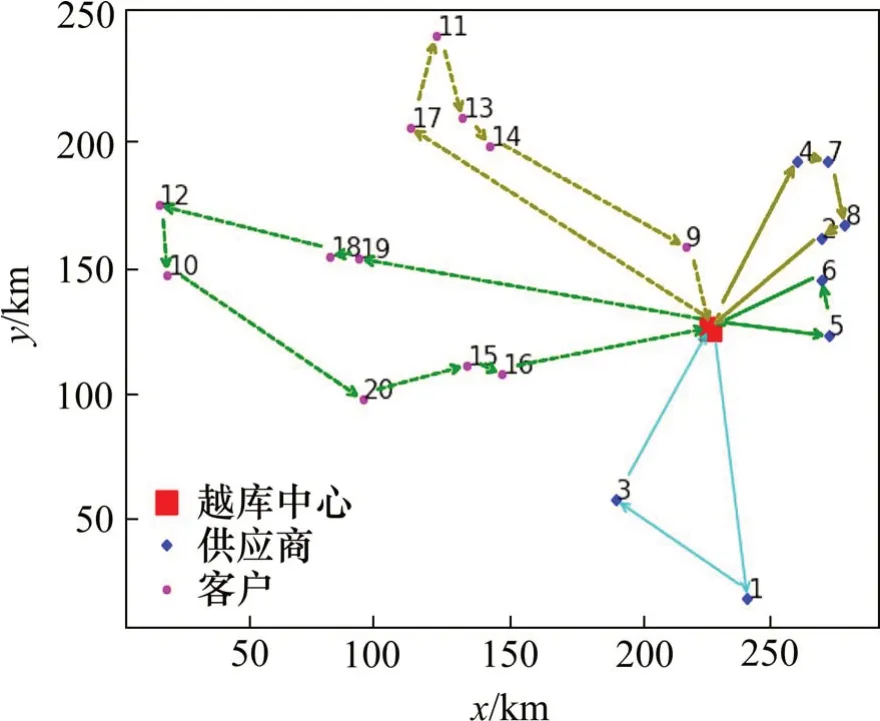
图3 算例20-2-0.4配送路线图Fig.3 Distribution routesof instance 20-2-0.4

图4为ALNS算法求解该算例的收敛曲线。算法在200代之前趋于稳定，400代左右收敛，说明本文设计的ALNS收敛性能良好。

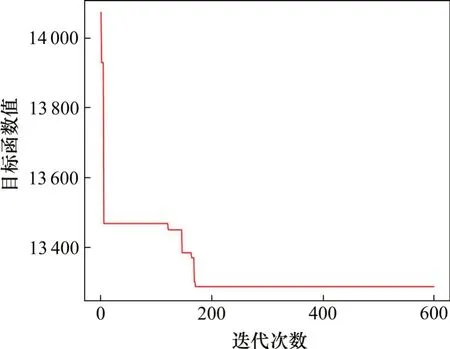
图4 算法收敛曲线Fig.4 Convergence curve of algorithm

3.2.2 不同优化目标下的结果分析

为分析不同优化目标对调度方案的影响，分别以总成本最低、车辆运营成本最低以及油耗碳排放成本最低为目标进行数值实验。表3展示了不同优化目标下目标函数值对比结果，其中MT表示总成本，MD表示车辆运营成本，MC为碳排放与油耗成本之和。

从表3可以看出：1)配送总成本(MT)方面，本文构建的模型平均总成本为21 555.6，而以车辆运营成本最低、油耗和碳排放成本之和最低为目标的平均总成本分别为22 192.5和21 579.6。比较而言，本文构建的模型平均总成本比以车辆运营成本最小为目标时减少了2.87%，比以碳排放和油耗成本最小为目标时减少了0.11%；2)车辆运营成本(MD)方面，本文构建的模型平均运营成本为2 188.6，比以碳排放油耗成本之和最低为目标平均减少了3.2%；3)油耗、碳排放成本(MC)方面，本文构建的模型平均油耗碳排放成本最低，且比以车辆运营成本最小为目标时减少了0.32%。以上对比结果可见，本文构建的模型能够有效地兼顾车辆运营成本、碳排放成本以及油耗成本。

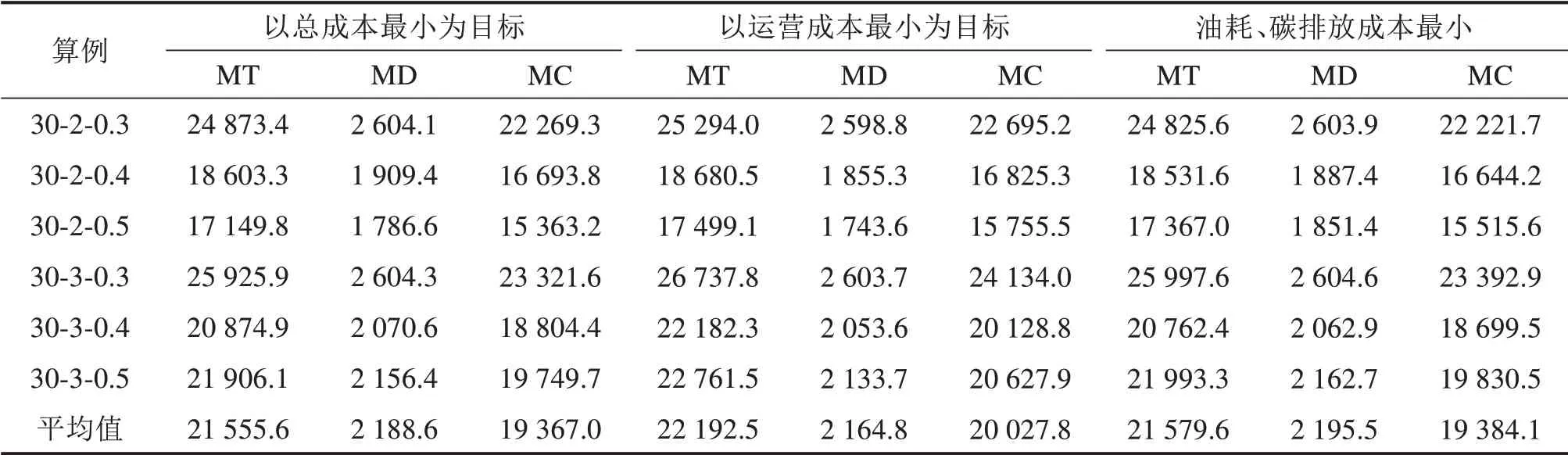
表3 不同优化目标下目标函数值对比Table 3 Comparison resultsof objective value under differentobjective

3.2.3 不同问题特征下的M-M GVRPCD结果分析

为分析不同问题特征对调度方案的影响，按照文献[10]规则生成了包含多种算例特征的算例集合2。为了使算例具有更一般性的特征，该算例中包含了C(聚集)和R(分散)2类算例，其中C类算例供应商与客户节点均匀分布于[0,100]*[0,100]区域内的4个角落，R类算例供应商与客户节点随机分布于[0,100]*[0,100]。为分析越库中心位置对总成本的影响，设定越库中心位置坐标为[50,50]，[50,60]，[50,70]3种情况，分别表示为D1，D2，D3；同时，考虑1，2和3 3种不同供应商-客户供需比，分别表示为DM 1，DM 2，DM 3。该部分以车辆运营成本、碳排放成本以及油耗成本之和最小化为目标，分析节点分布位置、越库中心位置、供应商-客户供需比等问题特征对车辆调度方案的影响，对比结果如图5所示。

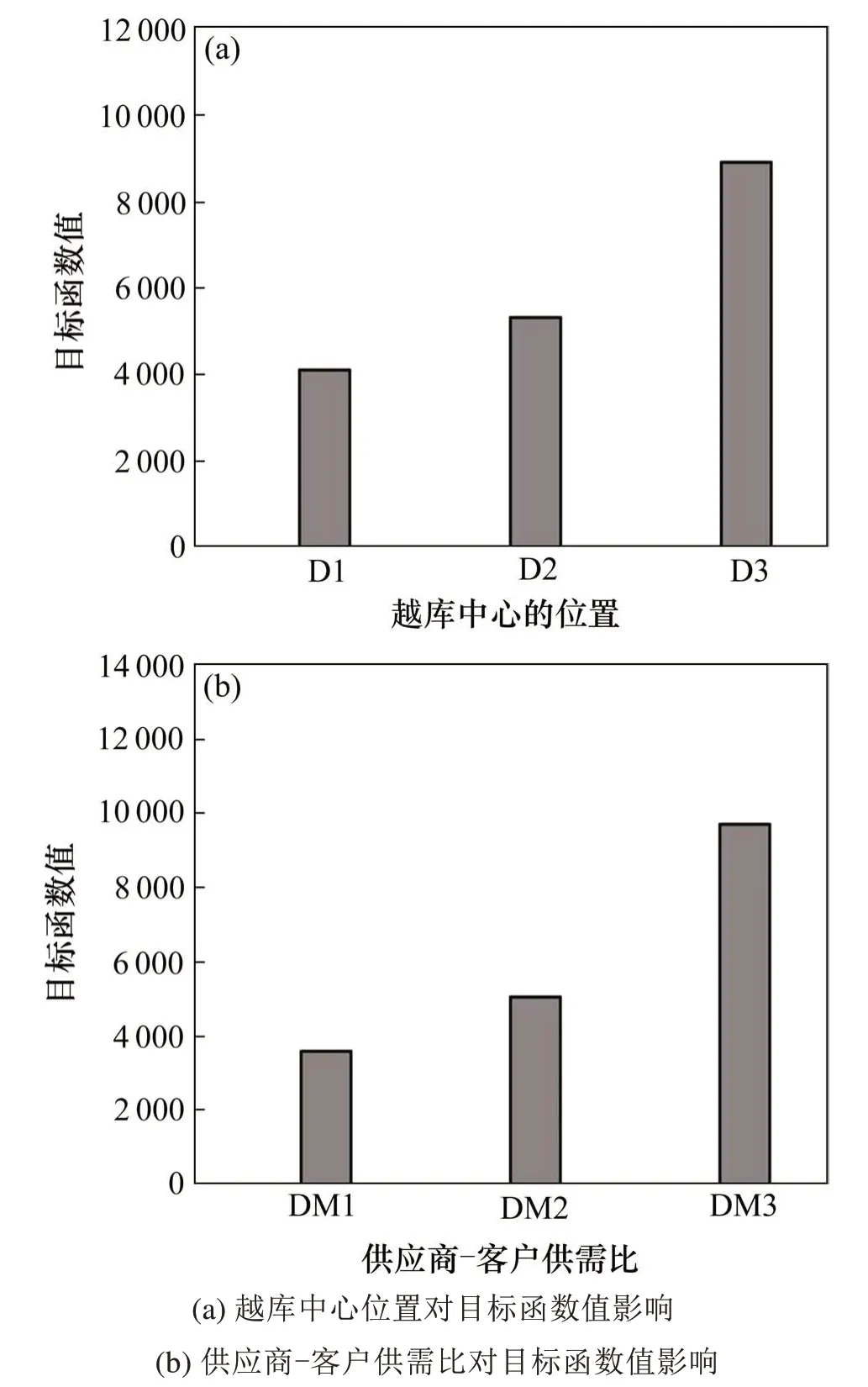
图5 不同越库中心位置与供应商-客户供需比下目标函数值对比Fig.5 Comparison resultsofobjective value underdifferent location of cross-docking and supplier-customer density

从图5(a)中可以看出，当算例的供需数量比相同时，随着越库中心位置的y轴坐标增大，目标函数值也相应增大。这主要是因为随着越库中心坐标值变大，越库中心的位置开始向边缘偏移，从而导致车辆往返越库中心的距离也相应增加。这说明越库配送网络设施布局对于总成本有着较为显著的影响，且当越库中心建设于配送网络中心位置时总成本最低。图5(b)所示，当越库中心位置相同时，供应商-客户供需比越大，平均目标函数值越大。针对所有算例，供应商-客户供需比为1时相对于供需比为2和3时总成本分别少41%和170%。这主要是因为供应商-客户供需比越大，单个供应商所服务的对应客户数越多，单个供应商所需要提供的货物量也相应增多。而车辆最大载重量固定，当供货总重量增大时，使用车辆数相应增加，从而造成配送总成本的增加。