融合车站分类和数据降噪的城市轨道交通短时客流预测
2022-09-23朱才华孙晓黎李培坤张景辰李岩
朱才华,孙晓黎,李培坤,张景辰,李岩
(1.长安大学 运输工程学院,陕西 西安 710064;2.西安交通工程学院 土木工程学院,陕西 西安 710300;3.北京交通大学 交通运输学院,北京 100044)
掌握城市轨道交通系统的特征,并基于此进行短期客流预测是城市轨道交通管理人员做出合理运营管理和控制决策的基础[1]。由于轨道交通客流的波动性和复杂性,导致原始客流数据受到外部环境干扰,客流存在较大的随机性,容易凸显某些随机波动[2]。同时,轨道交通车站建筑特征和周边用地性质的多样性,仅依靠全局预测,很难把握车站的特有特征。因此,掌握轨道车站自身特征和降低外部环境对客流数据干扰程度对提高轨道交通短时客流预测精度具有重要作用。短时客流预测主要服务于动态调度和及时信息服务,要求迅速准确地预测出可能出现的情况[3]。根据预测模型原理可分为线性预测模型和非线性预测模型[4]。已有的短时预测方法主要有时间序列法、支持向量机、卡尔曼滤波法和深度学习等[5-6]。自回归滑动平均模型(Auto regressive moving average model,ARMR)能够迅速对下一阶段的客流变化做出反应,不需要考虑变量的多样性,但运算简单导致其对随机波动不能进行过滤,容易对预测精度产生影响[7]。原始客流数据的复杂性易受到外部环境因素的干扰从而产生噪声[8],较多的随机波动导致预测过程中降低了预测结果的时效性。数据常用的降噪方法有标准差降噪、分箱降噪、孤立森林和小波变换等[9-10]。其中小波变换可以对细节分量进行阙值处理然后进行小波重构,有效降低随机波动和突发事件带来的客流干扰[11]。轨道客流的全局预测容易忽略车站客流特征带来的影响。服务功能不同的车站,其客流构造结构存在不同。轨道车站的聚类促进轨道客流预测的精细化发展。空间聚类算法[12]和时间序列聚类算法[13]广泛应用于轨道车站的聚类,但二者聚类因子数量有限,容易忽略其他因素的影响。K-means聚类作为无监督分类的一种方法,可以有效的发掘数据集的内部结构特征[14],同时K-means算法可考虑多个因素对同一对象产生的影响,聚类因子可由向量因素组成,保证分类因素的综合考虑。目前的研究忽略了车站客流特征和客流本身的随机波动,导致预测误差的增加。基于此,本文以城市轨道交通客流数据为研究对象,依据聚类算法对轨道车站进行分类,并探讨了不同类别车站降噪小波基的选取,采用组合模型确定了不同类别车站短时客流预测差异,并与单一模型预测精度进行对比。这项研究主要有3个贡献:1)依据轨道交通车站的客流属性和建筑属性,将车站进行分类,避免了不同类别车站自身特征被忽略。2)针对各类车站客流特征,选择合适的小波基对车站的原始数据进行小波变换,以减少原始数据中存在的噪声干扰。3)建立了WT-ARMA组合预测模型,可以在下一阶段快速、准确地预测客流量的变化。
1 预测模型的建立
1.1 车站聚类
聚类分析是根据事物的自身属性,按照一定的分类准则对所研究的对象进行分类。研究选用K-means聚类进行车站的划分。作为短时客流预测的基础,客流属性和外部建筑环境是影响预测结果的直接原因,因此,车站聚类因子是由客流差异性数据和外部环境因素组成。聚类因子的定义如下:
1)车站早高峰(7:30~8:30)进站(F1)/出站(F2)流量与全天进站/出站客流比,反映早高峰时段车站的客流特征。
2)车站晚高峰(18:00~19:00)进站(F3)/出站(F4)流量与全天进站/出站客流比,反映晚高峰时段车站的客流特征。
3)车站非高峰时段(10:00~16:00)进站(F5)/出站(F6)流量与全天进站/出站客流比,反映非高峰时段车站的客流特征。
4)车站周边用地混合度(F7)反映周边居民的出行规律,轨道交通步行衔接的合理范围是500~800m[15-16]。研究选用车站500m范围内的用地数据,并基于混合度熵进行求值。熵值为[0,1],值越大表示混合度越大,定义为M,则

式中:Pi为车站500m范围内第i种用地所占的比例;k为用地的种类数,本文共有8类用地,分别为行政办公、教育科研、商业金融、文物古迹、工业、医疗、居住和其他。
5)车站建筑强度(F8)是指车站周边500m范围内的建筑物容积率。
6)换乘客流中,公交车站与轨道交通接驳的适宜距离在200m以内[8,17],选取车站200m范围的公交线路数(F9)作为特征指标。
经过排序,将以上9个聚类因子共同组成一个向量因子F=[F1,F2,F3,F4,F5,F6,F7,F8,F9],此向量因子即为聚类的输入变量。
为了将数据缩放到相似的范围,使用ZSCORE方法对数据进行标准化处理。选用轮廓系数(Silhouette Coefficient)确定聚类数k的值[18],其值为[-1,1],越接近1表示内聚度和分离度都更优。
1.2 小波变换
小波变换通过对轨道客流的分解重构,从而达到降噪的目的。其核心是通过选择合适的小波基通过伸缩和平移对原始数据信号进行多维多尺度的细化分析。在任意空间L2(R)中,将f(t)函数通过小波基函数进行展开,这种展开就是连续小波变换,表达式为:

式中:a为小波基尺度,控制小波函数的伸缩;b为小波基平移量,控制小波函数的平移;x(t)为原始轨道客流信号;ψ(t)为母小波;ψa,b(t)为母小波经位移和伸缩产生的小波基函数。
在小波基的选取方面,考虑2个函数之间的互相关性,当小波基提取到的低频轮廓数据与信号数据之间的互相关系数最大时,此小波基可作为最合适的选择,表达式为:
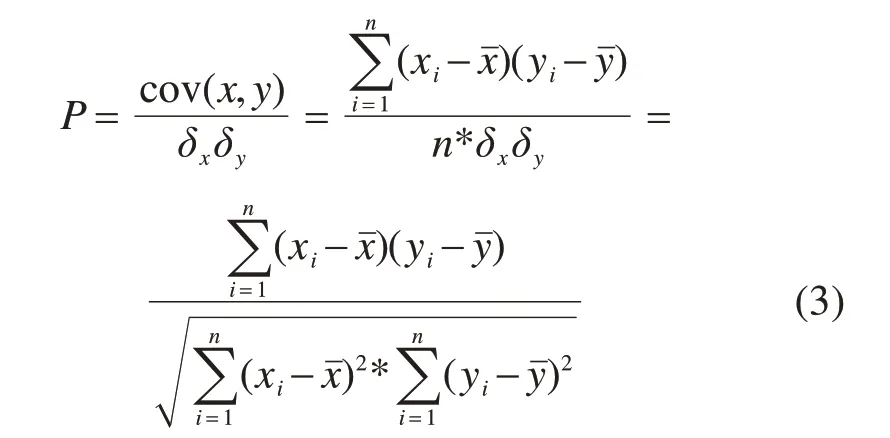
式中:P为互相关系数;x为低频段轮廓数据;y为真实信号数据;cov(x,y)为2个信号之间的协方差;δx,δy为2个信号之间的标准差;xi,yi为2个信号变量在i处的值;xˉ,yˉ为2个信号变量的平均值。
离散小波变换是按照2的幂级数进行离散化,分解的最高层次应为log2N(N为待检测信号的长度)[19]。在短时轨道交通客流预测中,关注高频信号的细节系数,在对轨道交通客流数据分解中应分解到小波变换所支持的最高层,此时既保证了客流原始变化趋势,又降低客流本身的随机波动。
1.3 ARM A预测模型
利用ARMA模型进行轨道交通的客流预测,对于时间序列F(t),若满足下面公式(4),称其为ARMA模型。
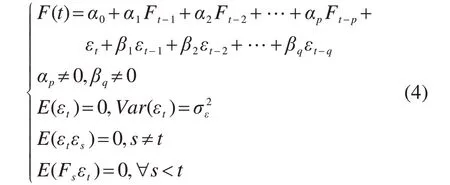
式中:p为p阶的自回归;q为q阶的滑动平均;αp为自回归系数;βq为移动平均系数;{εt}为白噪音序列;{εs}为t=s时的白噪音序列;为序列{εt}的方差值;Fs为t=s的时间序列。
自回归移动平均模型作为多元线性回归模型,又可以细分为AR模型、MA模型和ARMA模型。其中,AR模型认为随机变量的取值主要受前p期的序列值影响,记为AR(p);MA模型认为随机变量的取值主要受前q期的误差项影响,记为MA(q);ARMA模型认为随机变量的取值不仅与前p期的序列值有关还与前q期的随机扰动有关,记为ARMA(p,q)。因此,在进行预测之前需要解决2方面问题,分别是模型的识别和模型参数的标定。
自相关函数(autocorrelation,ACF)和偏自相关函数(partial autocorrelation,PACF)分别体现了样本数据的总体相关性和样本间变量相关性。因此可通过二者在滞后期所体现的拖尾和截尾特性对模型进行识别。不同条件下对模型的选择标准如表1所示。

表1 自相关函数和偏自相关函数性质Table1 Autocorrelation function and partialautocorrelation function properties
在对模型阶数p,q值进行判定中,贝叶斯信息准则(Bayesian Information Criterion,BIC)弥补了赤池信息准则(Akaike Information Criterion,AIC)估计容量较大的数据时产生的拟合误差,因此研究以BIC准则为基准来确定模型阶数。通常p与q值为1~20之间的整数,通过交叉验证求得使BIC最小p,q值。
2 实例分析
2.1 数据集
选择了2019年6月份西安地铁2号线的自动售检票(Automatic Fare Collection,AFC)数据来检验预测模型。AFC数据集包含时间戳、车站名称和各车站30m in内的进站和出站流量。
在分析中,为了适应周期性,选择6月1日-6月28日(共4周)的轨道客流数据进行预测分析,前3周的数据作为训练集,最后1周的数据作为测试集,预测时间间隔为30m in。
2.2 车站类型识别结果
从图1可知,当分类数为4时,轮廓系数最大,因此选择聚类数目为4。聚类结果如表2所示。表2中的类别为车站所属聚类簇,距离为车站与当前聚类簇中心的紧密关系,距离越小,代表车站更接近聚类中心,对于形成此类别的贡献度越大。

表2 车站聚类结果Table 2 Station clustering result
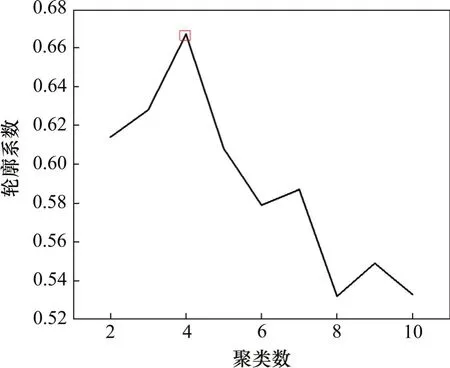
图1 不同聚类数对应的轮廓系数Fig.1 Silhouette coefficientsof differentclusternumbers
图2显示各类轨道车站当前时段进出站客流量与全天进出站客流量比值的变化趋势。4类集群分别代表了各个车站的典型特征:
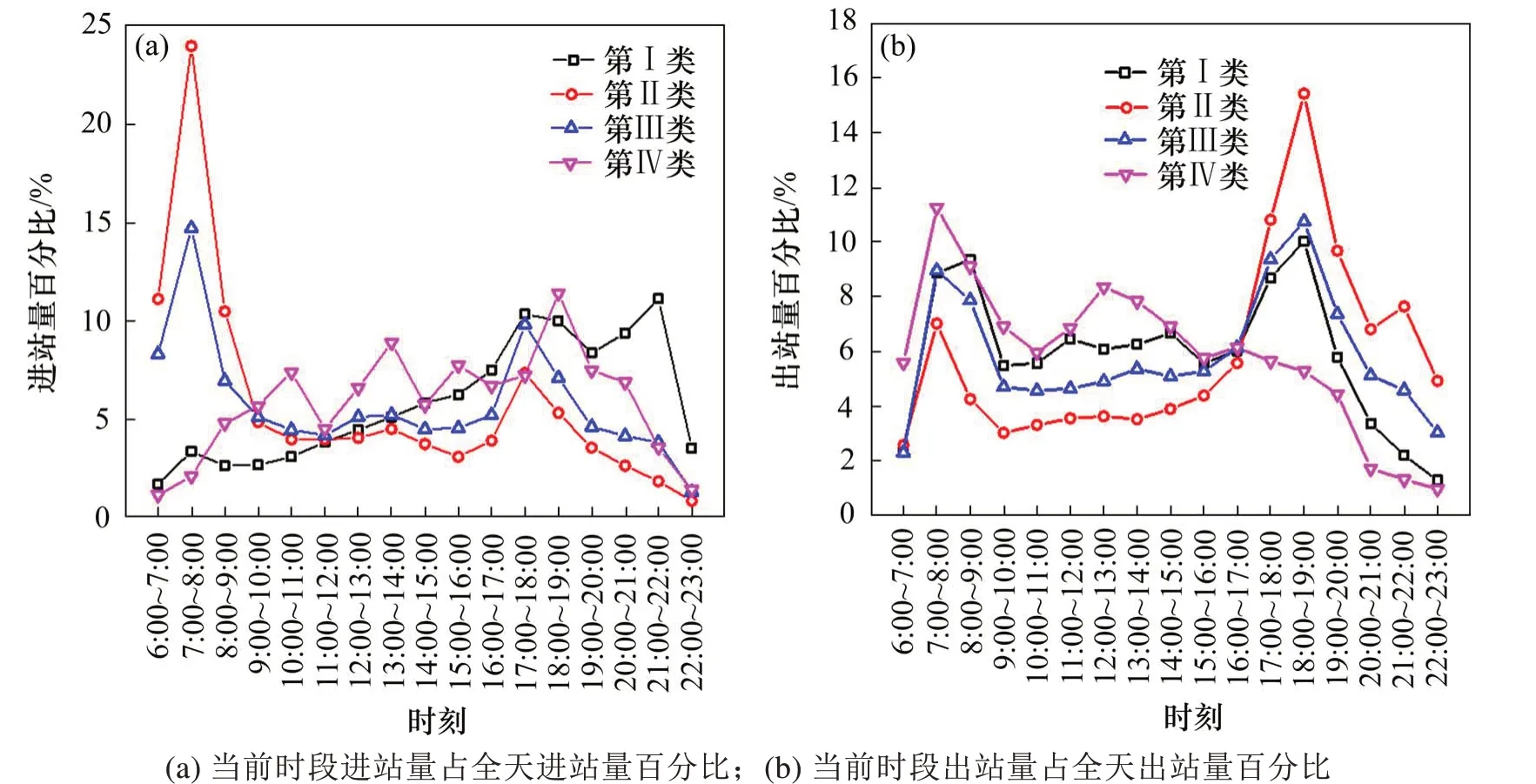
图2 聚类结果展示Fig.2 Clustering results display
1)第I类车站主要位于城市中心区域,早高峰进站客流很低,随后逐渐增长,而出站客流存在明显的早晚高峰,并且早晚高峰出站客流比例相近。这类车站周边有更多的商业和办公用地,因此将其定义为商业、办公车站。
2)第Ⅱ类车站潮汐性明显,早高峰进站客流比例很高,出站客流比例很小,而晚高峰进出站客流比例与早高峰现象相反。这类车站主要为通勤客流出行,因此将其定义为密集型居住车站。
3)第Ⅲ类车站数量最多,用地主要功能仍为住宅,但兼具商业和教育功能。客流潮汐性较Ⅱ类减弱,因此将其定义为轻型居住车站。
4)第Ⅳ类车站客流特征与一般消费、旅游的特征一致,早高峰为客流汇集地,晚高峰为客流发散地,因此将其定义为旅游文化车站。
在选择时,挑选距离中心最近的车站作为其所在类别的样本进行分析。其中,小寨为第Ⅰ类的样本;凤栖原为第Ⅱ类的样本;凤城五路为第Ⅲ类的样本;大明宫西为第Ⅳ类的样本。
2.3 小波变换分析
各类车站由于客流差异性,在降噪过程中要依据小波系结构与原始信号之间的关系选择合理的小波系进行降噪处理。考虑到小波基的正则性、对称性和线性相位等特性都会对原始信号的平移和伸缩产生影响,共选出8个小波系。各小波系提取的低频轮廓信号与原始信号之间的相关性如表3所示,根据互相关性,第Ⅲ类车站选择Daubechies小波系进行降噪处理,其余类别车站选择Bior‐thogonal小波系。根据客流时间长度,将数据分解到第10层,原始客流数据分解示例如图3所示。

表3 小波系与原始信号互相关系数Table 3 Correlation coefficientofwaveletsystem and originalsignal
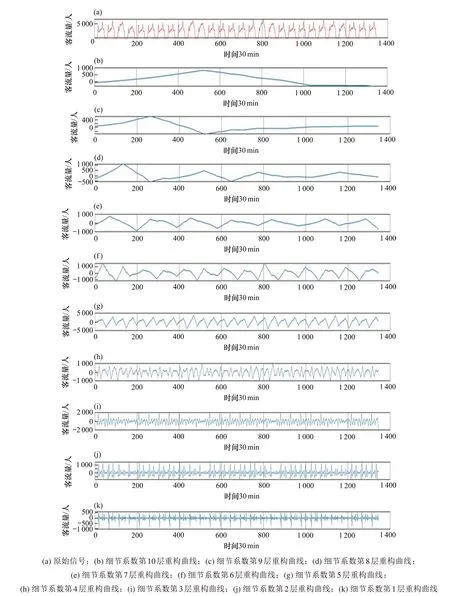
图3 轨道数据的小波分解示例Fig.3 Waveletdecomposition of orbitdata
小波变换通过对各层分解信号选择不同的阙值来实现其降噪功能,对于反映轨道客流短时变化特性的高频小波系数应选用高通过阙值。10~1层对应的高频信号系数降噪阈值分别为100%,90%,75%,50%,10%,0%,15%,20%,40%和70%。
轨道交通客流数据的重构为原始信号分解的逆运算,采用原分解小波基对降噪后的各频段分解系数进行重构。重构的新客流信号既能保证了原始数据的基本特征,又能反映客流数据的短时时变特性,同时,排除了噪声信号的干扰。降噪后的信号与原始信号对比如图4所示。
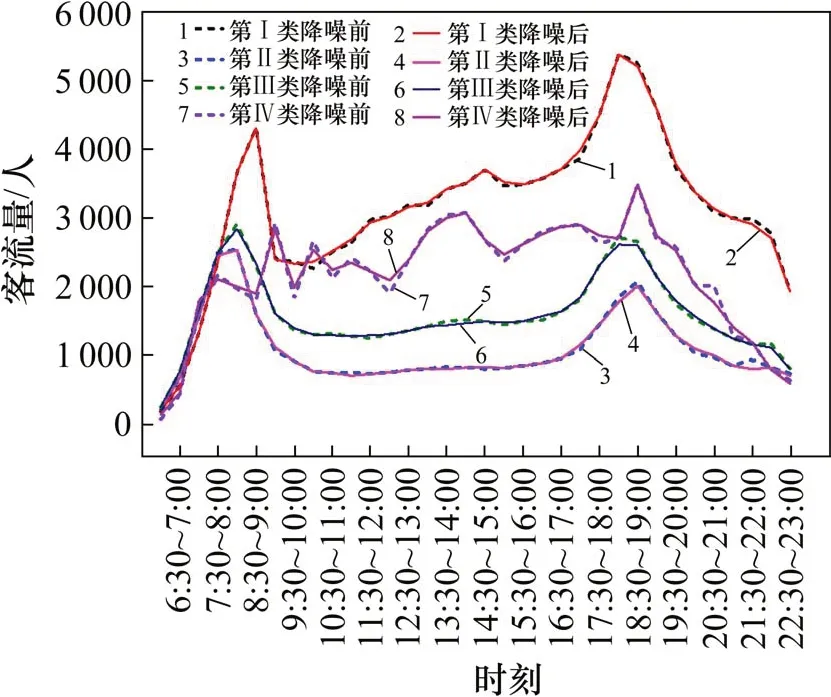
图4 原始信号与降噪信号对比Fig.4 Comparison of originaland noise reduction signal
2.4 预测结果分析
为了确定模型,分别对4类车站数据的拖尾和截尾情况进行判定,4类车站的自相关函数图和偏自相关函数图如图5所示。
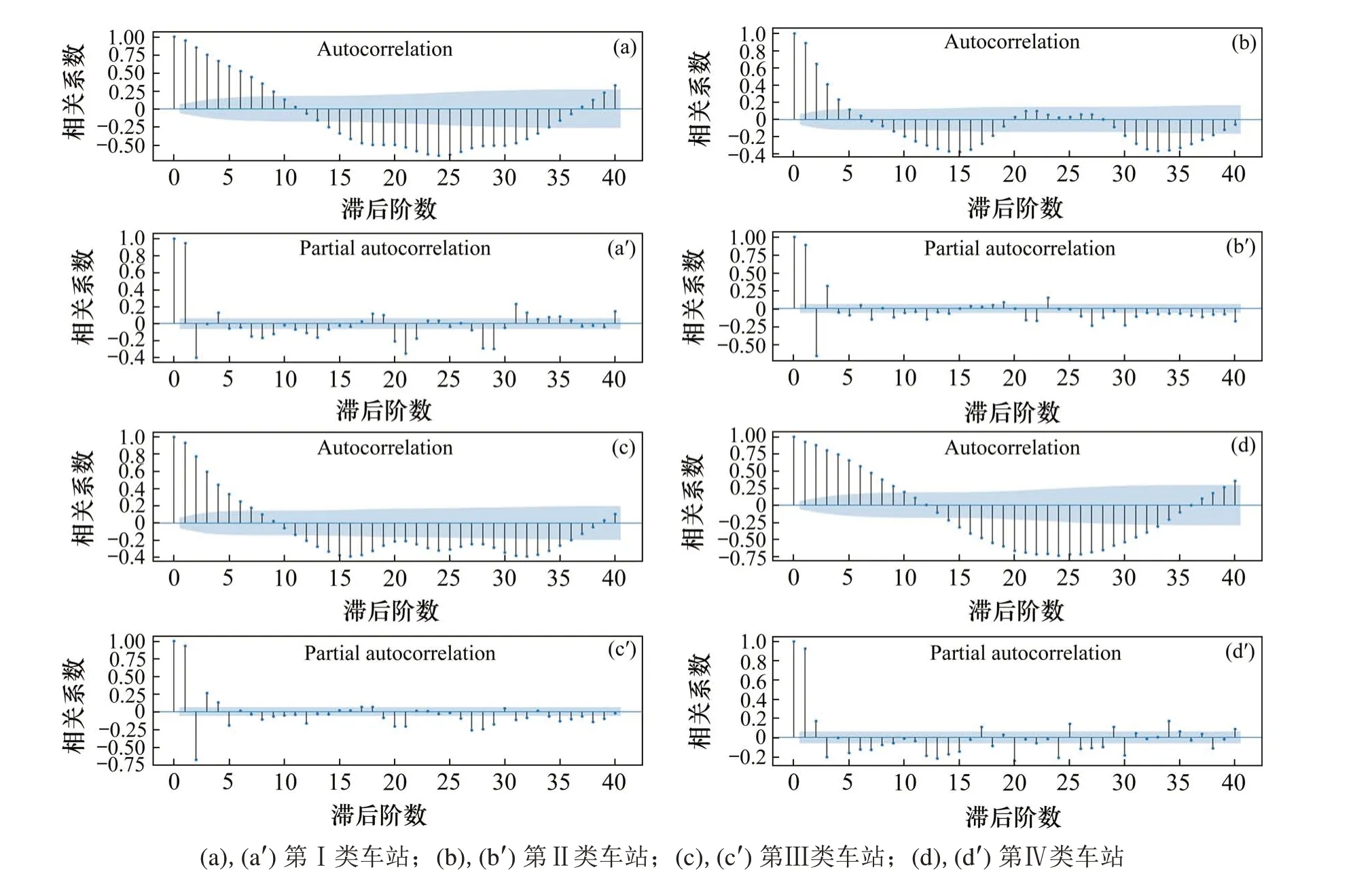
图5 客流量时间序列自相关和偏自相关函数图Fig.5 Autocorrelation and partialautocorrelation function diagram of passenger flow
从图5可知,这4类车站的自相关函数和偏自相关函数都具有明显的拖尾性,因此使用ARMA模型进行建模。通过BIC准则确定4类车站的模型阶数分别为ARMA(7,6),ARMA(5,6),ARMA(6,5)和ARMA(7,6)。
对4类车站的轨道客流量运用WT-ARMA组合模型进行预测,具体预测结果如图6所示。
从图6看出,组合模型可以较好地对客流进行短时预测。在预测性能的比较中,还对单一ARMA,支持向量回归(Support Vector Regression,SVR)和BP神经网络的预测效果进行统计。单一ARMA模型的参数设置与WT-ARMA组合模型相同,并于2.4节给出。SVR模型作为一种用于划分和线性回归的机器学习算法,可以剔除无用数据得到稀疏的解。影响SVR预测精度的参数主要为惩罚系数C和高斯核函数幅宽g,根据粒子群算法的适应度变化曲线[20]对参数进行确定,4类车站的最优参数(C,g)分别为(10.32,0.12),(12.33,0.17),(7.86,0.08),(15.37,0.15)。BP作为经典的神经网络模型,其网络层数和神经元数可视情况改变。BP神经网络的输入层节点数量基于滚动单元;输出层的节点数量由每日的预测时段数决定,研究的预测步长为1;隐藏层节点数量为模型训练误差最小对应的值。因此,本文将4类车站的参数设置为:输入层6节点、输出层1节点、隐藏层4节点、学习速率0.005,迭代至收敛。
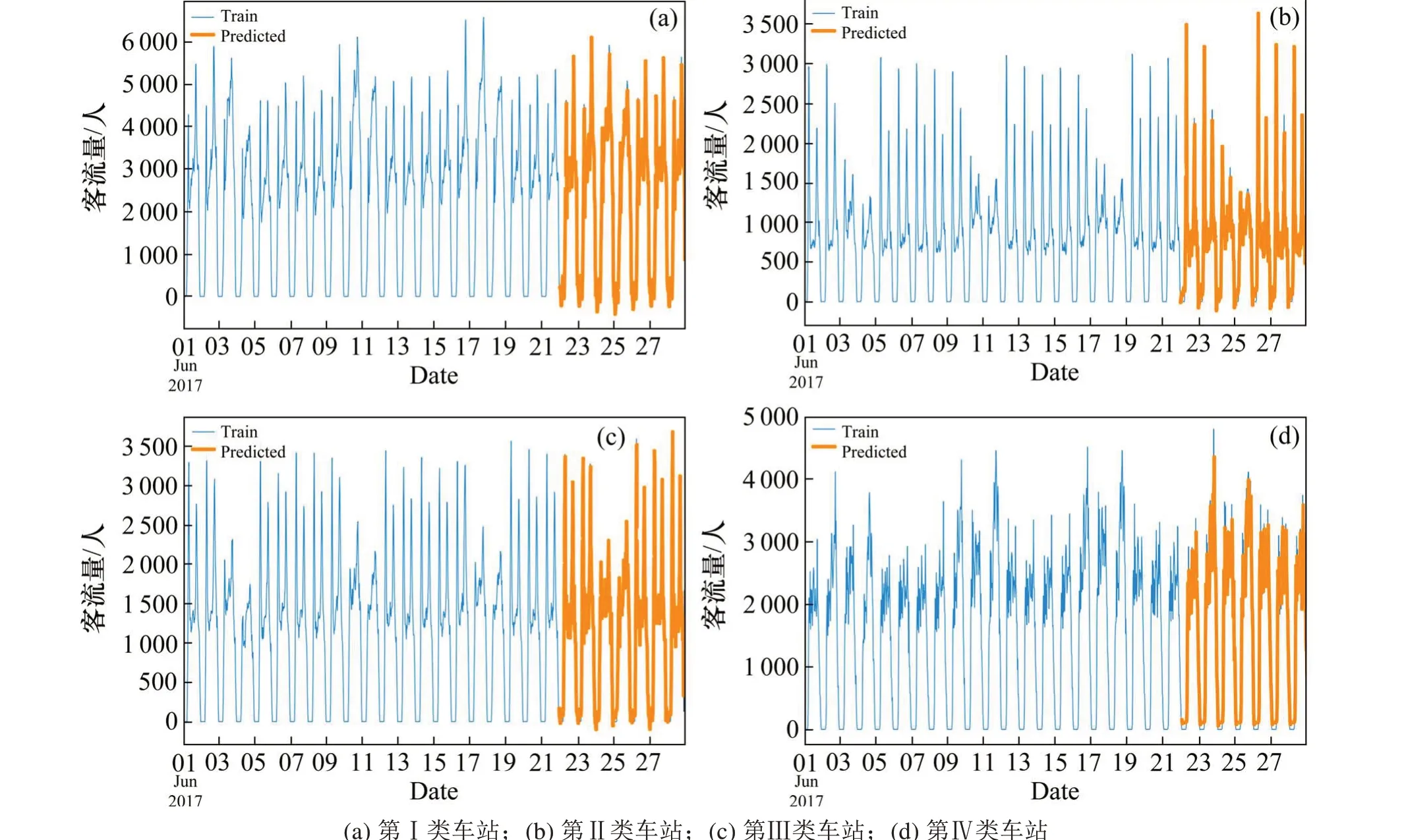
图6 WT-ARMA组合模型预测值与实际值对比Fig.6 Comparison of predicted and train valuesofWT-ARMA combinationmodels
利用最常用的统计指标,平均相对误差(MAPE)、均方根误差(RMSE)和拟合优度(r2)量化预测结果,同时运算时间作为时效性的考核指标。不同模型预测评价指标如表4所示。
从表4可以看出,组合模型具有更好的预测精度,SVR和BP神经网络的预测效果次之,ARMA效果最差。在时效性中,组合模型运算时间最快,ARMA与SVR次之,BP神经网络最慢,说明组合模型能够有效提高预测精度和时效性。

表4 各类车站模型预测评价指标Table 4 Various stationmodelprediction and evaluation indicators
组合模型对4类车站预测的精确度为:Ⅲ>Ⅰ>Ⅱ>Ⅳ。以30m in为时间粒度,分别统计不同日期、相同时间段的客流相关性,采用皮尔逊相关系数(Pearson correlation coefficient)进行描述。皮尔逊相关系数值在0~1之间,以0.2数量级递增,其相关性逐渐增强。不同时段客流自相关性如图7所示。
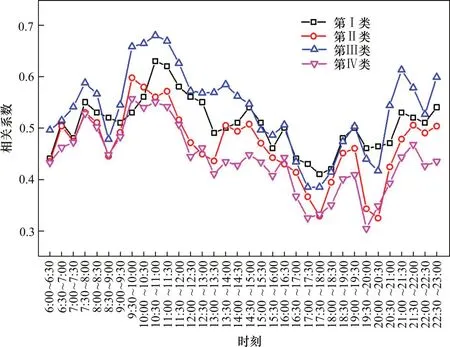
图7 客流相关系数Fig.7 Correlation coefficientof passenger flow
图7显示,第Ⅲ类车站客流具有强相关性,同时这类车站预测精度较高,第Ⅳ类车站客流的相关性较弱,这类车站预测精度较低,说明客流的预测精度与客流的内部相关性还存在关系。
3 结论
1)在基于聚类算法对车站分类的基础上建立WT-ARMA组合模型对各类车站轨道客流进行预测。所建立的模型可有效、准确、快速地预测短时轨道交通客流量。
2)选用车站自身属性和周边环境因素作为变量,利用K-means聚类方法,对车站进行分类。西安市地铁2号线的各车站可划分为商业、办公车站,密集型居住车站,轻型居住车站和旅游文化车站。
3)与单一ARMA,SVR和BP神经网络模型相比,WT-ARMA的组合模型具有更高的预测精度和更短的运算时间。
4)研究对影响预测精度的因素和产生预测误差的原因进行分析,在后续研究中将进一步讨论特殊节假日大客流爆发的因素。
