基于卷积长短期记忆网络的泄漏监测算法研究
2022-09-23韩佳豪陈小华姜海斌赵涓涓
韩佳豪,陈小华,姜海斌,李 霖,李 振,张 皓,赵涓涓
(1.太原理工大学 信息与计算机学院,山西 晋中 030600;2.国家管网集团西南管道有限责任公司,成都 610000)
长距离输送管线的泄漏检测系统是管道储运行业的重要课题。截止2020年底, 我国境内已经罕见尚未安装泄漏监测系统的石油及天然气长距离管线[1]。若从监测泄漏所依据的数据源分类,相关研究工作大致可分为基于流量数据的方法和基于压力数据的方法,两种方法各有其适用范围及亟待改进的内容[2-3]。
基于流量的泄漏监测方法是历史最为悠久的方法,其原理为实时地读取流入与流出管线的流量数据,并根据沿线的温度、压力以及高程等推算管线容积的变化。在此基础上求出流入流量、管容变化量、流出流量三者之间的平衡关系,并由此判断是否发生了泄漏。流量平衡检测方法的准确性很大程度上依赖流量计量装置本身的性能,采用高精度流量计算机通常可以获得更为满意的结果;其次取决于计算管道容量的方法。由于长输管线的压力与温度采样点间隔很大,通常均为几十公里,中间数值无法直接测量,只能用插值或模拟等方法近似求出,所以管道容量计算的结果往往很难与实际情况完全吻合,制约了流量平衡算法的整体精度。此外,目前所见的流量平衡算法均需要在监测管道的两端安装同档次流量计,而目前我国的部分用户仅在管道输出端安装有流量计,在输入端一般采用测量储油罐液位的方式计算输入管道的物料,其精度相比流量计较低,在使用流量平衡泄漏监测时误差很大,限制了这一方法的应用。
基于压力数据的泄漏监测算法是近年来长输管道泄漏监测的研究热点[4],其中基于负压波的方法和基于音波(包括次声波)的方法构成了研究的主体内容[5-6]。负压波和音波技术的主要差别在于传感原件与信号处理电路的不同[7]。在对信号进行分析的基础上又分为侧重于压力数据基波(时域)特征的方法[8],侧重于时、频域结合的方法[9],以及重点研究低频谐波[10]的方法等。但各种基于压力数据的监测算法均以发现平稳状态下管道流体中突然出现的压力波变化信号为起点,即以平稳信号中的突然变化点作为监测泄漏的关键目标。
基于压力数据的算法通常在两种情况下容易发生错误:一种是压力下降过程中没有特征点。典型的例子为非法盗油时刻意缓慢平稳地打开阀门,在此状态下泄漏的时段内并不存在明显的压力突变,从而使得基于压力变化的监测算法无法发现泄漏,造成漏报;另一种是压力变化过程中发生了多个突变点。典型例子如间歇地打开阀门过程中形成的台阶状递减压力形态。由于在泄漏区间内发生了多个近邻的压力突变点,监测算法往往难以确定各个突变点与其压力波之间的时间对应关系,所以很大概率会导致计算错误,造成误报。这两个问题在基于压力数据的泄漏监测算法的发展过程中一直未能得到妥善解决。
为了开发新的泄漏监测算法,近年来的研究工作在泄漏信号处理方式与挖掘信号本身特征方面进行了广泛地尝试。李传宪等[9]通过改进小波滤波的阈值函数来提高滤波效果,并使用盲源分离方法,结合频域特征,在长度为370 m的实验管道上更为准确地捕获到了泄漏信号。YU et al[11]运用在图像处理领域取得了良好成绩的双树复小波变换和奇异值分解作为主要手段来处理音波信号,在3 km长的实验管道上稳定地实现了泄漏监测功能。在挖掘信号特征的研究方面,孟令雅等[12]采用相关函数与协方差函数对管道上的常见干扰信号进行分类,通过排除法发现泄漏信号,并在总长度为251 m的实验管道上证明了该方法的有效性。上述几种新技术均被证明可以有效地改善泄漏监测过程中漏报与误报的问题,但目前尚未见到上述成果在长距离工业输油气管道上获得应用的报道。
除了上述几种新近发表的泄漏检测技术之外,采用压力数据进行监测泄漏时还有基于压力梯度的算法。早在19世纪,达西-魏斯巴赫(Darcy-Weisbach)就推算出了的水头损失计算公式,并证明了管道中的流量与沿线的压力梯度之间存在着确定性的关系,这一成果在后来被不断地完善更新[13]。近期研究的基于该理论的工作无论是将其用于数值模拟的计算基础[14],或在长度约为200 m的实验室管道上进行的实验[15],均再次证明了该理论的正确性。但同样由于管道沿线的各种参数并不一致,通常也不能密集地逐点测量,因此采用显式数学方程式的方法。这种“白箱”的方法往往很难在长距离管道上得到压力梯度与实际流量之间的准确系数。与此同时,近年来在各个领域中大获成功的深度学习方法,为在管道输送工业中以“黑箱”方式探索这种对应关系提供了一条新的解决途径。近期的研究工作包括CAI et al[16]使用通过两层卷积神经网络对由麦克风采集的音频信号进行分类,在长度约为60 m的实验室管道上进行的实验,与KAMPELOPOULOS et al[17]发表的研究工作都是将深度学习技术应用于管道泄漏监测的典型案例。
基于上述内容,提出一种基于卷积长短期记忆神经网络(CNN-LSTM)的流量预测方法。将卷积网络的空间解析能力与长短期记忆网络的时序解析能力相结合,采用在现役管道运行过程中获取的大规模压力与流量数据训练出短时段平均压力梯度-平均瞬时流量的深度学习网络模型。使用该模型可以实时根据管道上的压力梯度来预测同一管道中的流量。目前达到的误差范围最小0.3%,最大0.7%,平均0.5%(相对管道瞬时输量),具有一定的实用价值。将其用于泄漏监测可以连续监视预测流量与真实流量的偏差,从而发现泄漏。在此基础上,可以采用压力曲线距离算法来进一步确定泄漏位置。在国家管网集团云南某成品油管线上进行的现场实验表明,相比现有的各种泄漏监测与定位算法,本算法简单有效,在泄漏量超过0.7%干线流量时均能报警,同时在管线设备操作期间不易产生误报。此外,新算法的重要意义还在于可以在管道一端安装了流量计的情况下使用,为尚未在管道两端,或未在管道的每个分输点均安装有流量计的用户提供了一种通过压力梯度变化发现流量异常情况的新手段。
1 网络构架
卷积长短期记忆网络(CNN-LSTM)是一种复合型网络。将深度神经网络联合或组合起来使用可以有效地利用各种网络特有的优势,近年来在各个领域均有成功案例[18-19]。
1.1 CNN网络
CNN网络[20]是前馈型神经网络的一种,主要由卷积层与池化层构成。由于采用了稀疏连接与权值共享等优化策略,在保证输入数据经平移、旋转、与缩放后特征保持不变的前提下,有效地减少了网络参数。CNN网络中的卷积层包括若干个特征面,每个特征面上包含若干个神经元,每个神经元通过卷积核与上一层特征面上的某个区域相连接。一个输入序列的特征在各个特征面上被分解,通过一系列卷积计算被提取出来。与卷积层相连接的池化层具有相同数目的特征面,可以再次提取特征量并降低相关参数的维度。由于长输管道的压力与流量数据均为时间序列数据,因此很适合采用一维卷积神经网络进行处理。一维卷积运算可以表达为:
(1)


(2)
重复对每个窗口为r的连续向量进行最大池化运算,即可求出最大特征序列。
1.2 LSTM网络
长短期记忆神经网络(Long Short-Term Memory,LSTM)[20]是对早期循环神经网络(Recurrent Neural Network,RNN)做出的重要改进,发表以后在处理时间序列方面取得了令人瞩目的成功。LSTM在网络结构中提出了遗忘门,输入门与输出门的概念与操作,从而有效地克服了原RNN网络容易发生梯度消失或梯度爆炸的弱点。图1为LSTM单元的逻辑结构图。当t时刻的数据Xt输入某个LSTM单元时,与t-1时刻的长期状态Ct-1以及输出ht-1共同参与运算,得到该时刻本单元的输出ht,即所求t时刻的预测数据。LSTM的更新公式可以表达为:
it=σ(Wi·[ht-1,xt]+bi) ,
(3)
ot=σ(Wo·[ht-1,xt]+bo) ,
(4)
ft=σ(Wf·[ht-1,xt]+bf) ,
(5)
Ct=ft⊗Ct-1+it⊗tanh(Wc·
[ht-1,xt]+bc) ,
(6)
ht=ot⊗tanh(Ct) .
(7)
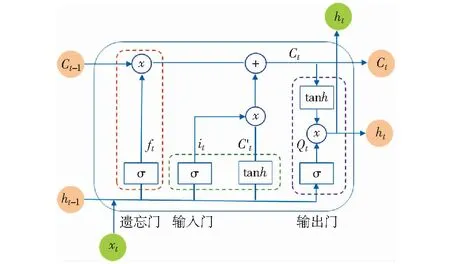
图1 LSTM单元逻辑结构图Fig.1 LSTM unit logical structure diagram
式中:ft为遗忘门的输出信号,其值决定了记忆单元C的遗忘比例;it为输入门信号,其值决定了当前输入信息输入到记忆单元中的信息量;Wi、Wo、Wf分别为输入门、输出门、遗忘门的权重函数;bi、bo、bf是偏置矢量,σ(*)为sigmoid激活函数;tanh(*)为双曲正切函数。由公式(6)、(7)可知,输入量到达LSTM的隐含层之后,首先经过输入门进行非线性变换,然后与经遗忘门处理后的记忆单元的状态相加,形成新的记忆单元状态。产生系统隐含层的输出ht前需再执行一次点乘运算,参与运算的项即为经过tanh处理后的新记忆单元的状态与经过经非线性函数处理后输入信息的状态。
1.3 CNN-LSTM组合模型
由于长输管道的压力梯度与管道流量之间存在确定关系,因此可以采用流量与沿线的压力采样点的数据作为模型的输入训练模型,预测在新压力条件下的流量。模型可以表示为:
(8)
(9)
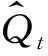
(10)
对于不同的管道,数据模型的具体参数需根据该管线的情况而调整,即需要设定压力梯度变量的数量i、回溯时间的深度j与流量计的个数k.图2为本项目中用于实验与验证的模型结构示意图,其中i=3,j=6,k=1.

图2 本项目实验管段卷积长短时网络(CNN-LSTM)模型及参数Fig.2 Model and parameters of CNN-LSTM tested in this project
1.4 数据预处理方法
为了提高预测精度,对于参与计算的压力与流量数据采用了不同的处理方法。
1.4.1压力数据
现实世界中的长输管道与试验室环境下的短距离管道有很多不同,其中最重要的不同为长距离管道上压力数据中的高频分量对信号特征值的贡献很小,通常均为毫不相干的近场噪音。文献[21]通过实验证明了在工业长输管道中最有价值的信号波段集中在0~3 Hz范围内。因此,对在长输管道上采集的压力数据而言,信号中的高频分量可以作为噪音滤掉,反而有益于提高预测精度。所以压力数据除了应进行标准化转换之外,还应先期进行滤波处理。图3为数据样本的制作流程, 简化起见,其中省略了关于处理缺失数据等常规数据清洗的步骤。
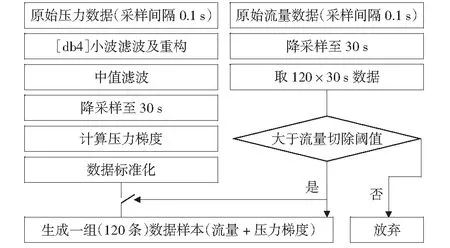
图3 数据样本制作流程Fig.3 Data sample making process
1.4.2流量数据
与压力数据不同,流量计算机瞬时流量信号中的高频分量包含了有价值的特征信息,不宜作为噪音被消除。由于本项目流量数据的变化范围相对狭窄,因此可以不用进行任何预处理。这样系统输出的预测值也无需再作反变换运算。若流量计数据在实际应用中波动范围较大,可以先进行线性缩小后再输入网络,获得预测结果后再作同比例放大,但通常不需要进行滤波处理。
1.4.3时间片选取
时间片的长度对预测结果准确性具有直接影响。时间片太短会造成数据中的随机参量得以显现,导致预测精度下降;时间片太长则会减弱有价值的波动数据,同样使得预测精度下降;此外时间片太长还将导致用于训练网络的样本数量下降,造成模型的泛化性能不强;经实验发现在本应用中时间片长度在20~40 s之间为宜,本文模型中时间片长度为30 s.
1.4.4回溯时间深度
选取回溯时间深度时,应考虑将压力梯度对流量影响的延迟时间包含在内。例如,在管道起点处关阀动作引起的压力变化出现在相邻管段上的延迟为1秒以内;但对管道末端流量产生的影响,根据管道的长短不同,要在若干秒到若干分钟后才会出现。因此在回溯时间深度的选取上,需要根据影响管线压力设备的位置、设备到流量计之间的距离、以及压力波传播速度来计算延迟时间。
1.4.5模型训练
依照图3流程生成数据样本后,即可开始按批量(batch)抽取数据来训练模型。目前常用的深度学习平台均集成有模型训练的函数可供调用,通常仅为一条fit(…)语句。作为普通用户只需保证样本数据的正确性与合理性,将存放样本的数据的数组输入模型即可开始训练过程。深度学习是对所见数据间关系的一个解析过程,实践证明训练模型的数据样本越多越好,但同时还应注意让模型“看到”数据关系之间的各种情景,模型的预测能力在很大程度上取决于训练样本的规模和丰富程度。
1.4.6评估模型误差
对于回归模型,通常采用平均绝对误差(Mean Absolute Error,MAE)及其百分比来评价预测的准确性。MAE计算公式为:
(11)
式中:m为评估数据数目;fi为第i个预测值;yi为与预测值所对应的实际值。
1.5 泄漏点定位
基于CNN-LSTM的泄漏监测算法的主要流程如图4所示。当发现实际流量与预测流量的偏差超过阈值时,可以通过计算各管段压力波形曲线的距离以确定压力扰动源的位置,计算时应使用经过滤波且采样间隔为0.1 s的压力数据,以提高定位精度。近期发表的文章中介绍了将曲线距离计算应用于泄漏点定位的方法[22]。通过曲线距离求导压力扰动位置的方法消除了因个别奇异值对整体定位结果的干扰,是一种行之有效的方法。实践中发现将动态时间弯曲算法(Dynamic Time Warping,DTW)[23]应用于经滤波后的压力数据具有更好的鲁棒性,可以充分发挥DTW算法自动匹配波峰与波谷的能力,为本项目所采用。DTW采用了动态规划DP(dynamic programming)的方法来进行时间规整的计算,是一个典型的优化问题。主要包括两个步骤:
1) 计算压力波形曲线序列各个点之间的距离,形成距离矩阵M(i,j).
2) 寻找一条从矩阵左上角到右下角的路径,使得路径上的元素和最小,递推规则为:
Lmin(i,j)=min{Lmin(i,j-1),Lmin(i-1,j),
Lmin(i-1,j-1)}+M(i,j) .
(12)
式中:Lmin(i,j)表示矩阵左上角(1,1)到任意一点(i,j)的最短路径长度。
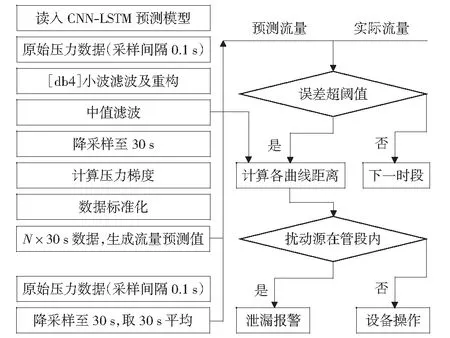
图4 泄漏监测算法流程Fig.4 Leakage monitoring algorithm flow
2 实验与验证
课题组在国家管网集团云南某成品油管线上,选择中间站到末站一段安装了4个压力数据采集器,采集点间隔分别为59.8 km、60.0 km和42.9 km.测试段管线沿线高程呈馒头状并在末站前约15 km处达到最高点。测试管线最大高程差约为150 m.该成品油管线采用间歇方法运行,每次输油过程为3~5 d,在中间站有分输,输油过程中有频繁地流量调节、油品切换以及储油罐变更等操作。这样使得输油时沿线压力变化频繁且复杂,使其测试环境具有挑战性。
2.1 预测模型训练与测试
实验系统搭建完成后,课题组采集了2021年4至8月之间共5个月的数据,其中4-5月份和7-8月份的数据用于训练模型,6月份数据被用作模型的验证使用。图5为实验段管线2021年6月期间4个压力测量点数据变化全貌图。图6为同期的流量数据总览图,由于汽油流量与柴油流量分别由两台流量计算机计量,因此在图中表现为两条各自独立的曲线。
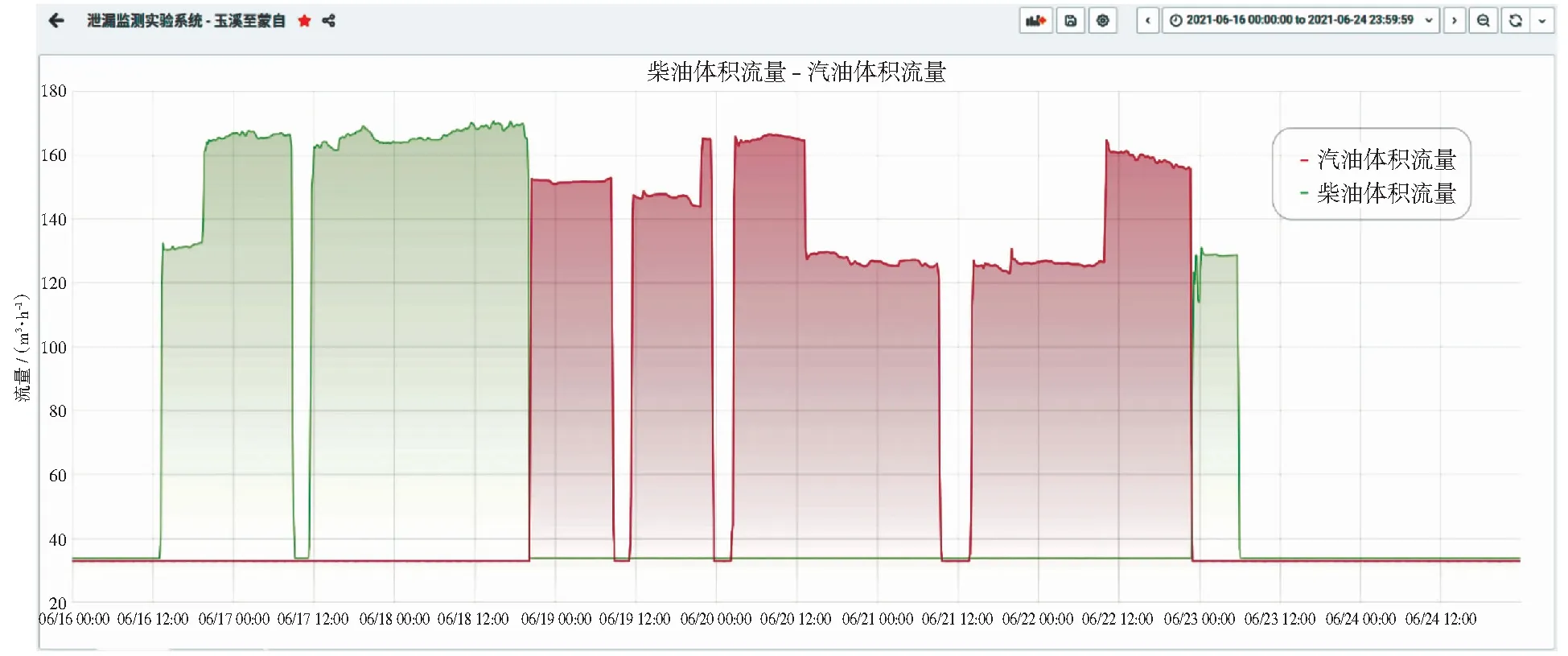
图5 实验管段6月份压力数据Fig.5 Pressure data of experimental pipe section in June
图6 实验管段6月份柴油及汽油体积流量Fig.6 Volume flow of diesel and gasoline in the experimental pipe section in June
模型训练完成后,以不在训练数据集中的6月份的数据作为测试数据集进行测试,其结果如图7所示。从测试结果看到,预测数据与实际数据能够很好地吻合,包括停止输送、开始输送、调节流量、切换油品、以及切换末站储油罐的完整过程。测试集的平均绝对误差在平稳段为0.3 m3/h,波动段为0.7 m3/h,整体误差范围为该管道实时输量的0.3%~0.7%以内。测试中发现基于组合式深度学习模型的泛化能力良好,表现为在对输送两种油品时的预测精度并无差别,包括在管道内存在不同长度的混油段的情况。
2.2 现场放油测试
将模型用于实际系统之前,将现有的全部监测数据统一用作训练数据重新训练模型,最终获得现场使用的深度模型。结合文中介绍的泄漏监测定位算法,建立了泄漏监测现场实验平台。实验时分别在实验段管线的8#阀室(距离流量计26 km)与4#阀室(距离流量计133 km)进行了放油测试。测试中使用了涡轮流量计以及数控球阀。采用数控球阀可以对开阀速度、阀门开度、以及阀门运行方式进行精确控制,特别是可以完成诸如缓慢匀速开阀、阶梯状开阀等动作,为测试算法提供了必要的技术保障。

图7 6月份流量数据真实值与预测值对比Fig.7 Comparison between the real value and predicted value of traffic data in June
测试时的两种开阀方式为:
1) 缓慢开阀:阀门根据指定开到位时间除以阀门终止角度匀速运行至开到位。
2) 间断开阀:阀门以0.3 s运行、0.3 s停止的方式运行至开到位。
图8为其中某次放油时真实流量与预测流量的数据曲线。从图中可以看出,在测试油阀处于关闭状态下,本文提出模型的输出预测值与柴油体积流量实时平均值保持一致,当测试放油阀打开时,模型预测值会有明显提高,激发系统发出预警。表1为测试结果总结,分别对8#阀室和4#阀室采用缓慢和间断两种开阀方式以不同速度进行现场放油测试,两个阀室报警时间差均低于1 min、泄漏定位误差均低于1.5%.
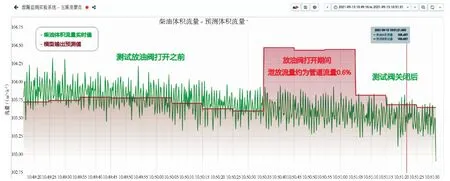
图8 放油实验时实际流量与模型预测流量曲线Fig.8 Curve of actual flow rate and model predicted flow rate during oil discharge experiment
2.3 实验对比
为了验证所提组合模型的有效性与优越性,将CNN-LSTM组合模型分别与仅拟合空间特征的CNN和序列网络中另一典型模型循环神经网络(Recurrent Neural Network,RNN)[24]进行对比。放油测试实验环境统一选定在实验段管线的8#阀室、开阀方式和开到位时间统一选择缓慢30 s和间断20 s.表2总结了这些常用模型的方法和测试结果。实验表明,组合模型CNN-LSTM可以有效拟合时间与空间特征,在缓慢和间断两种开阀方式下,监测效果都明显优于仅拟合空间特征的CNN模型和时序网络RNN模型,可高效准确监测管道泄漏事件。
3 结束语
1) 通过构建CNN-LSTM深度网络,在实际的长输管道上初步实现了用压力梯度准确预测实时流量的深度模型,并将之应用于管道的泄漏监测。新算法可以有效监测出压力平稳并缓慢下降过程中的泄漏事件,也可以发现压力波动过程中流量的异常情况,弥补了现有泄漏监测算法的不足。
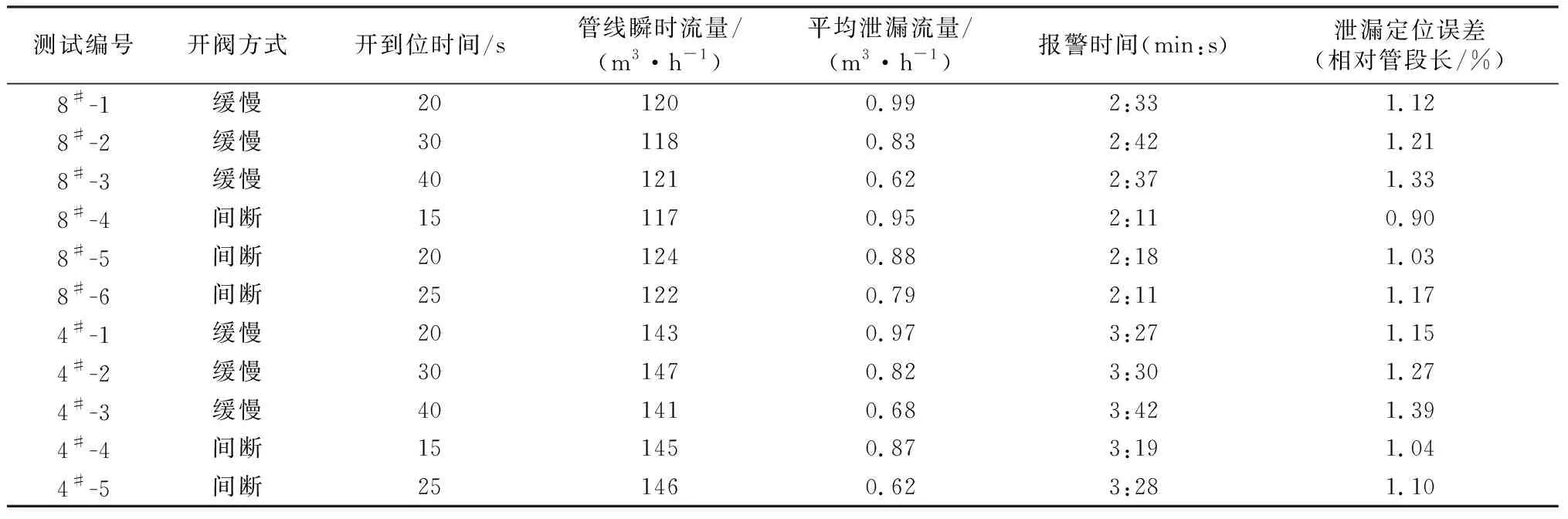
表1 现场放油测试结果Table 1 Results of field oil discharge test
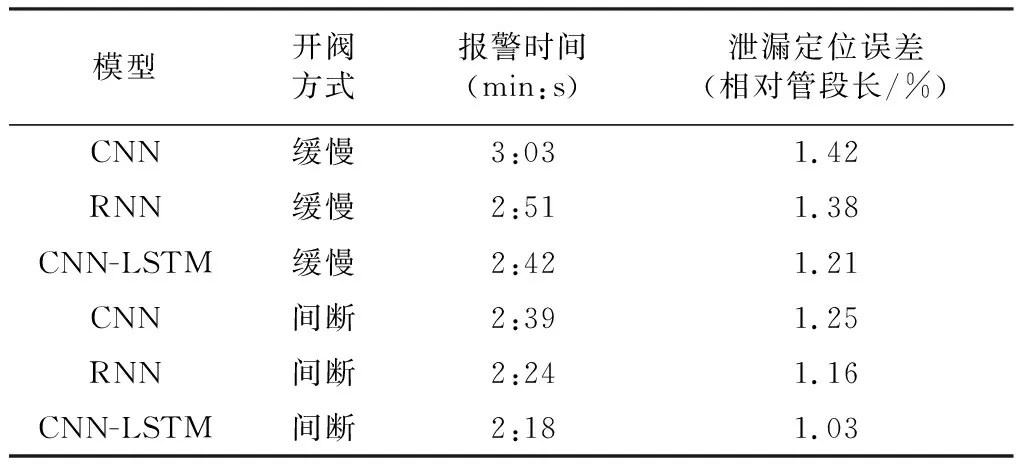
表2 不同模型现场放油测试结果Table 2 Field oil discharge test results of different models
2) 由于采用了短时段平均数据,相比其它基于压力数据的泄漏监测算法,本文算法的泄漏检测系统在设备操作过程中不易发生误报。
3) 本算法可以通过压力梯度预测管道上一个或多个流量输入或输出点,为在管道上仅安装了单个流量计的用户,或具有多个分输管道、安装有多个分输流量计的用户提供了一种监测流量异常变化的新手段。
