基于LQR和PID的智能车轨迹跟踪控制算法设计与仿真

徐明泽，刘清河

(哈尔滨工业大学(威海)汽车工程学院，山东 威海 264209)

智能车轨迹跟踪的精确性及稳定性是车辆安全自主行驶的基础，主要研究内容通过相应的控制策略尽可能使智能车实际行驶的路线接近已规划好的车辆路径，使实际路径相对于预期路径的横向偏差与航向偏差尽可能小[1-3]。智能车的轨迹跟踪控制主要包括纵向的速度跟随控制以及横向的轨迹跟随控制。横向控制主要是根据横向控制算法控制转向轮转角或转向盘转角，从而使其能够精确跟踪上期望轨迹。纵向控制主要是调节智能车的驱动和制动，从而使其达到跟踪期望车速的目的。

目前用于智能车辆的轨迹跟踪技术的相关控制算法包括模糊逻辑控制算法、滑模控制算法、模型预测控制算法以及最优控制算法等[4-6]。模糊控制方法适用于车辆的状态未知的情况，且可以选用较为简单的模型，但是人为判断较强，缺乏一定的理论性[7-8]。滑模控制的优点在于能够很好地匹配车辆模型，缺点是在高速时未考虑动力学约束、控制不稳定[9-10]。模型预测控制建模方便，能够及时补偿模型误差，控制较为精确，但是涉及到大量约束条件时，处理非线性最优问题的计算量增大，实时性会降低[11-12]。

对于轨迹跟踪横纵向控制的问题，国内外许多学者都对此进行了研究。文献[13-16]提出了新的横纵向跟踪控制方法，其中文献[13]针对智能车辆动态系统高度非线性和不可匹配性，使用基于逆推的变结构控制设计横向和纵向组合运动控制器；文献[14]在七自由度车辆动力学和非线性轮胎模型的基础上，利用神经网络PID算法及模糊预瞄理论对车辆进行轨迹跟踪的横纵向控制；文献[15]提出一种视觉预瞄式横纵向耦合控制，将预瞄距离和车速同时引入到模型预测控制器中；文献[16]等以模型预测控制为基础，提出一种全新的横纵向控制算法。文献[17]基于一种全自动制导框架研究汽车纵向和横向耦合问题，采用非线性模型预测控制的转向控制。文献[18-19]则进一步设计了横纵向控制器，其中文献[18]设计了横纵向控制系统，在综合道路曲率和纵向车速最优的情况下，搭建最优驾驶员横向控制模型。并使用纵向模糊控制算法控制油门、制动压力，最后基于纵向车速将其耦合；文献[19]设计了基于闭环驾驶员模型的纵向-横向控制器，该控制器通过预测车辆前方的路径来调节转向角和油门/制动压力。

LQR控制算法的控制对象为线性系统，评价指标为被控制系统的状态变量的二次型积分，其最优控制律通常可以通过求解Riccati方程得到，因此可达到闭环控制的目的[20-21]。而现有的LQR横向控制算法会存在一定的稳态横向偏差，并且在曲率快速变化时超调比较严重。在此基础上加以改进，提出了一种具有前馈的LQR轨迹跟踪控制算法，这样稳态横向偏差就能被很大程度的消除掉，并采用遗传算法确定其参数，减小计算量。使用PID控制算法可以提高纵向速度控制的精确性，进一步减小轨迹跟踪偏差。因此，本论文在横向控制上采用线性二次调节器 (linear quadratic regulator，LQR)，在纵向控制上采用双PID的控制方法来进行车辆轨迹跟踪，能够根据路径偏差进行实时调节，明显提高了车辆轨迹跟踪的控制精度和稳定性。

1 车辆跟踪误差模型

1.1 车辆动力学模型

为了保证车辆跟踪轨迹的精确性和实时性，本文采用车辆二自由度动力学模型，其微分方程如下：

(1)

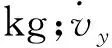
上述为非线性模型，对于控制器的设计来说过于复杂，因此需要进一步简化为线性模型。首先，对前轮转角δ进行小角度(小于5°)假设，即cosδ=1；其次，轮胎模型可以被简化为轮胎侧偏力和侧偏角的一次线性关系，即

Fyf=Cαfαf,
Fyr=Cαrαr.

(2)

式中：αf，αr为车辆前轮、后轮的侧偏角，rad；Cαf，Cαr车辆前轮、后轮的侧偏刚度，N/rad.

由于线性化轮胎模型只在轮胎侧偏角较小时具有较高的拟合精度，则用小角度假设可以得到车辆前后轮的侧偏角：

(3)

将公式(2)和公式(3)联合代入公式(1)可得到车辆动力学方程的矩阵形式：

(4)

1.2 跟踪误差模型

跟踪误差模型是智能车辆轨迹跟踪控制中常用的车辆运动模型之一，如图1所示。其中，距离偏差ed定义为车辆质心位置到参考轨迹投影点处的直线距离，θ、θr分别表示为车身纵轴线和参考轨迹在P点处切线的航向角，则航向偏差eφ=θ-θr.在本文中，为了便于与式(4)中的车辆动力学方程相联系，将航向偏差公式中的航向角θ替换为横摆角φ.由于车辆的航向角θ与横摆角φ之间相差一个质心侧偏角β，那么eφ可以近似等于φ-θr，但是其稳态误差不为0，为-β.

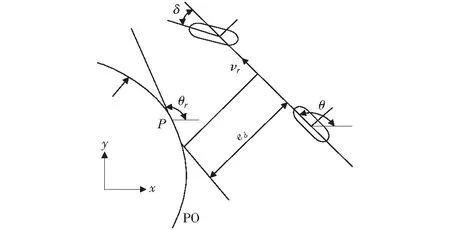
图1 车辆跟踪误差模型Fig.1 Vehicle tracking error model

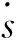
(5)

当航向偏差eφ足够小时，车辆质心处的距离偏差ed和航向偏差eφ可以表示为：

(6)

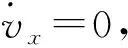
(7)

将公式(6)和(7)代入到公式(4)中，整理可得：

(8)

可将式(8)改写成状态空间方程形式，则有

(9)

式中：

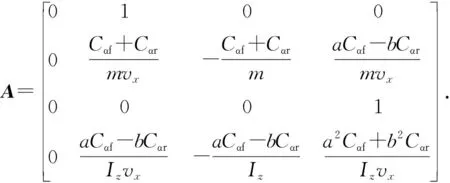
2 横纵向控制器的设计

2.1 横向控制器的设计

LQR控制算法方法的控制效果比较稳定，可利用较小的控制量使系统误差趋于零，且同时可以对不稳定系统进行整定[22]。本文所设计的横向控制器的算法流程如图2所示，其中矩阵A，B的计算已经在前文给出，在这里该模块不再叙述。

2.1.1最优LQR控制计算

LQR控制算法就是确立最优控制u*(t)=-Kerr(t)，使得下列性能指标函数达到最小值[23]。

(10)

式中：Q为半正定实对称常数矩阵，反映了对状态量的权重；R为正定实对称常数矩阵，反映了对控制量的权重。

为使性能指标函数J取得最小值，以达到能量消耗以及动态误差的综合最优，首先构建哈密尔顿函数：

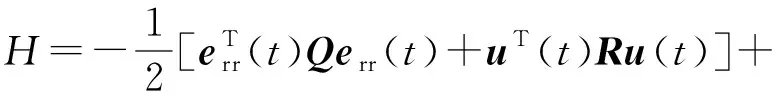
(11)

当输入信号没有约束时候，对式(11)进行求导，令其为0，得到最优控制信号为：

u*(t)=R-1BTλ(t) .

(12)

式中：λ(t)的值可以由λ(t)=P(t)err(t)给出，P(t)为以下方程的解：

PA+ATP-PBR-1BPT+Q=0 .

(13)

上式为黎卡提方程。式(13)经过求解后可以求得矩阵P，由此可得到最优控制律反馈矩阵K=R-1BTP，K=[K1K2K3K4].

由于车速vx与K为一一对应关系，为提高控制系统的计算速度，本文首先离线计算出不同车速vx和K的对应表，实际计算中可通过查表来获取不同车速下的反馈矩阵，提高横向控制的实时性。可利用Matlab中的lqr(A,B,Q,R)求解函数进行K的求解。

2.1.2离散轨迹点误差矩阵及曲率计算

一般来说，规划出的期望轨迹可以按照规划时间离散化成轨迹点，不仅可以更方便地求出投影点，方便接下来的计算，而且不需要处理多值问题。求解其误差及曲率的步骤如下：

1) 根据离散轨迹规划点的位置，找到与车辆真实位置(x,y)最近的点，称为匹配点。定义匹配点所在的序列记为dm，则匹配点坐标记为(xdm,ydm)，匹配点处所在切线的航向角记为θdm，匹配点处的曲率记为kdm.

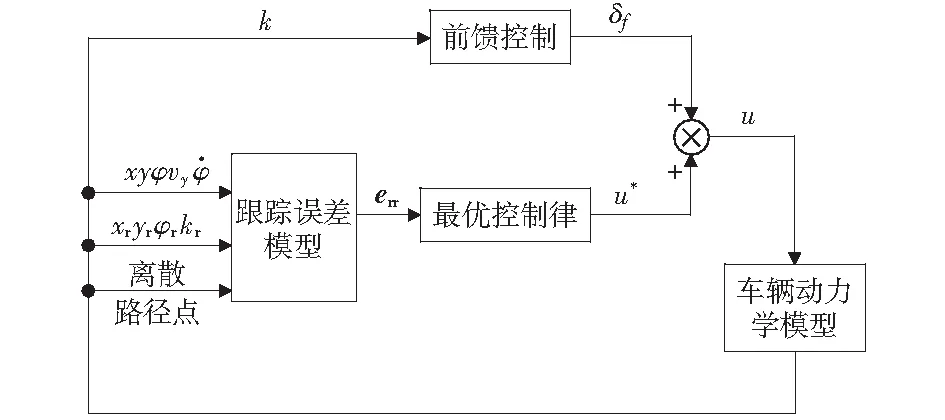
图2 横向控制算法流程图Fig.2 Flow chart of lateral control algorithm

2) 由于匹配点与投影点的弧长比较小，本文假设匹配点到投影点的曲率不变，即kr=kdm；假设匹配点到投影点的轨迹可以用圆弧来代替，得到控制位置偏差es，即es=-(x-xdm)cosθdm+(y-ydm)sinθdm.因此，可以计算出匹配点到投影点的距离偏差ed，即ed=-(x-xdm)sinθdm+(y-ydm)cosθdm.

3) 由曲率和匹配点到投影点的弧长的定义式可以求出投影点处所在切线的航向角，即θr=θdm+kdmes.那么，根据投影点处的航向角可以求得航向偏差，航向偏差的导数及速度偏差的导数，如式(14)：

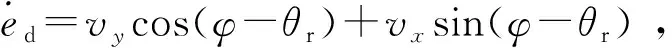
(14)

(15)

2.1.3前馈控制计算

将之前计算出的最优控制律u*(t)=-Kerr(t)代入到式(9)中，得到系统的稳态反馈状态方程

(16)

引入最优LQR反馈控制的目的是在车辆能顺利跟踪到期望轨迹的基础上，尽量去减小横向误差。但是由式(16)可知，无论反馈系数K取何值，汽车在横向运动过程中的横向偏差和横摆角偏差，即err和err的导数都不可能同时为零。因此，需要原来的控制律的基础上加一个合适的前馈控制量δf，来抵消稳态状态下的横摆角偏差，前馈控制的控制规律为：

u=-Kerr+δf.

(17)

将公式(16)代入到公式(17)中，可得

(18)

当系统稳定后，使得err的导数为零，由此可得

(19)

对式(19)计算并化简求得

(20)

式中：K1和K3分别为第一部分计算出的反馈矩阵K的第一和第三项。

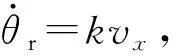
(21)

式中：k为第二部分计算出的曲率。

2.2 纵向控制器的设计

2.2.1PID控制算法原理

PID控制器的输出可表示为：

(22)

式中：KP为比例系数；KI为积分系数；KD为微分系数；t为时间；τ为积分变数。调节比例系数KP可快速、及时、按比例调节偏差，提高控制灵敏度；调节积分系数KI主要用于减小稳态误差，提高控制精度；调节微分系数KD能减小超调量、提高控制稳定性。

在本文中，通过反复调整参数，为了满足低中高3种仿真工况的普适性，以及同时兼顾控制精度和稳定性的要求，所采取的系数如下：KP=3；KI=0.01；KD=1.

2.2.2双PID控制算法

(23)

因此，本文设计了双PID控制器，分别对车速和位置进行控制，其控制目标分别为控制速度偏差ev和控制位置误偏差es，从而能够达到实时调节的目的。

2.2.3驱动制动标定表的制作

在制作油门刹车标定表之前，首先应该确定所采用的驱动/制动模型。由于本文的仿真对象为电动SUV，因此采用电动机模型，具体可描述为

P=Tn.

(24)

式中：P为电机所需功率，n为电机所需转速，T为电机的转矩，即

(25)

式中：Tmax为电机的最大扭矩，N·m；thr为加速踏板或制动踏板的开度；nb为基速，r/min，即最大功率Pmax与最大扭矩Tmax的比值。

根据此模型，可以利用仿真实验，得到速度、加速度和加速踏板或制动踏板的开度的三维散点，再利用双线性插值算法把未知的速度v、加速度a所对应的加速踏板或制动踏板的开度thr计算出来，得到关于这3个物理量的一个表格关系，即驱动制动标定表，如表1所示。其目的是根据车辆行驶过程中的速度和加速度值来实时控制车辆的加速踏板或制动踏板的开度，从而控制车辆的驱动或制动。

表1 驱动制动标定表Table 1 Driving braking calibration table

3 轨迹跟踪控制仿真

本文将通过Carsim与Simulink的联合仿真来验证上述的轨迹跟踪控制算法的效果，仿真流程图如图3所示。

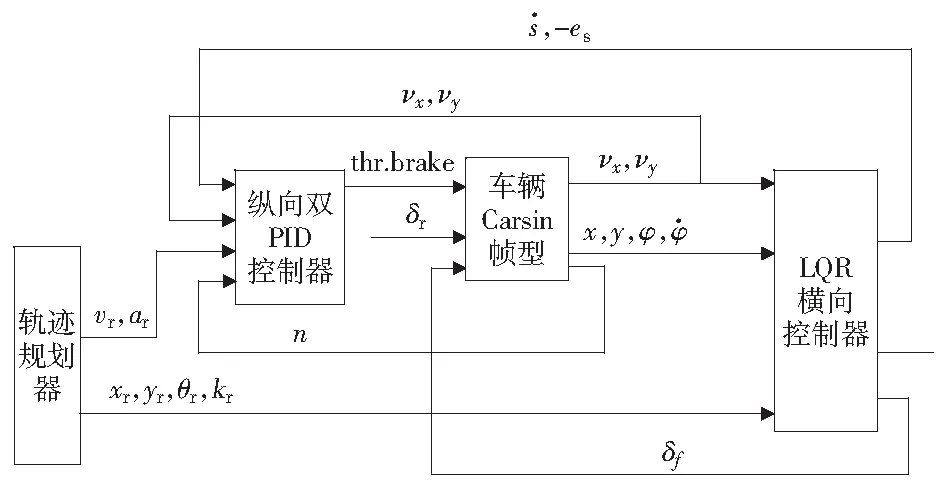
图3 联合仿真流程图Fig.3 Joint simulation flow chart

3.1 参考轨迹设计

为了更好地实现跟踪效果，所设计的参考轨迹的位置、速度、加速度、航向角、曲率在每一时刻应连续。基于五次多项式曲率连续平滑，无较大突变且舒适性较好(Jerk变化率比较小)的优点，本文采用5次多项式进行参考轨迹的设计，可表示为

xr(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5,

yr(t)=b0+b1t+b2t2+b3t3+b4t4+b5t5.

(26)

式中：a0，a1，…，a5，b0，b1，…，b5为待定系数。

另外，根据常见的行驶场景以及城市道路工程设计规范[24]，规划出的参考轨迹需满足起点和终点的边界条件：

其中，T为从起点到终点所行驶的时间，xend为终点的横坐标，通过设置不同的边界条件，进而解出式(26)对应的待定系数a0，a1，…，a5，b0，b1，…，b5.同时，将y(x)转换成y(t)，便于纵坐标的计算：

(27)

进而可以计算出参考轨迹的切线角θr和曲率kr：

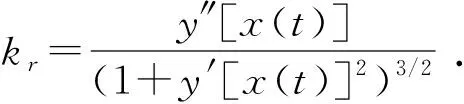
(28)

最终规划出的参考轨迹还应该对加速度进行限制：

(29)

3.2 仿真参数设置

3.2.1车辆参数设置

本文试验车型为SUV轿车，在Carsim中进行车辆相关参数设置，具体参数如表2所示。

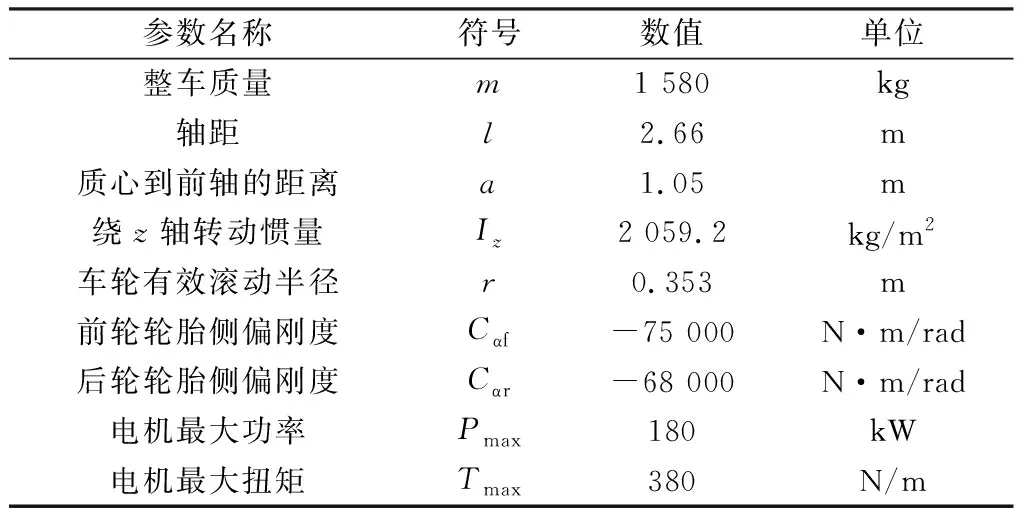
表2 车辆基本参数Table 2 Basic vehicle parameters

3.2.2仿真工况设置

本文所设置的仿真工况有低速大转角、中速小转角、高速小转角，分别对应道路停车、城市道路变道、高速公路变道3种工况，具体参数如表3所示。默认起点处的横向位移和纵向位移为0，并设定纵向速度和加速度为0，以及起点处和终点处的横向加速度为0，进而可以求得五次多项式的系数，得到参考轨迹。

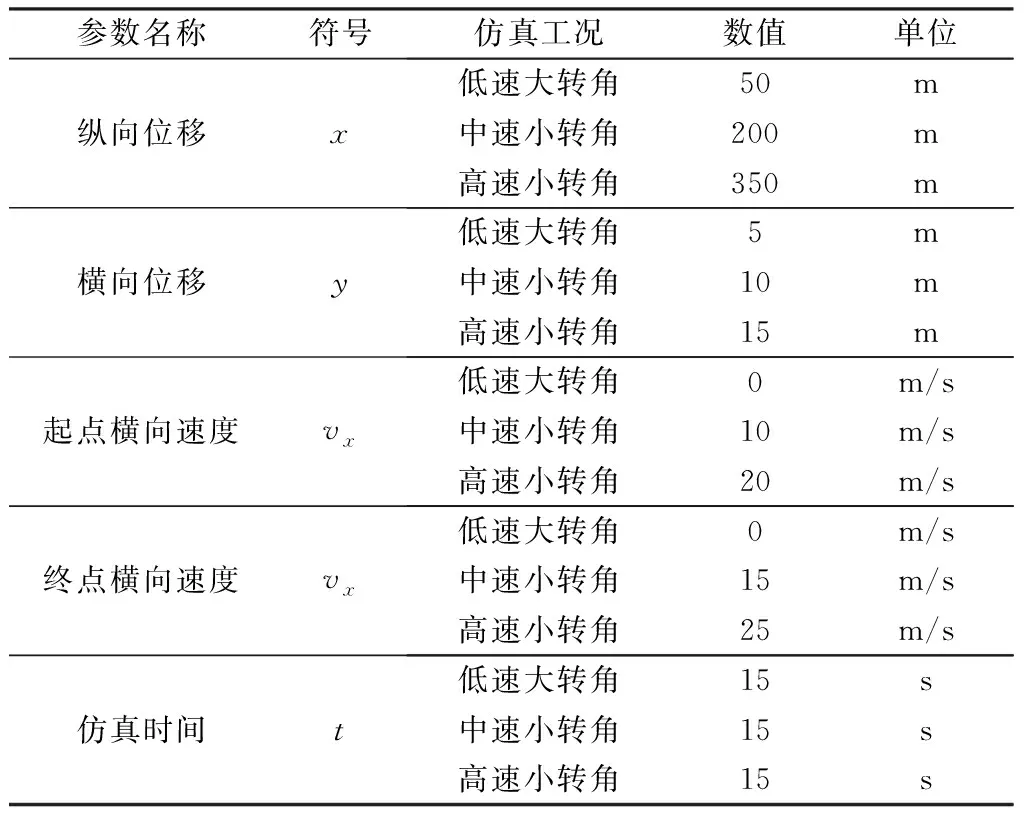
表3 仿真工况设置Table 3 Simulation condition setting

3.3 LQR参数确定

通常情况下，LQR算法的参数确定通常依靠人工试凑的方法，不但耗时耗力，没有科学的规律和求解方式，而且还不能保证LQR控制器发挥出最佳的跟踪效果[25]。针对无法选取最优加权矩阵参数Q和R的问题，本文采用遗传算法(GA)对加权矩阵Q、R的对角线参数进行求解，使LQR控制器具有优良的鲁棒性，并使车辆能够较精确的跟踪到参考路径。

通常情况下，Q值增大可以提高系统的响应速率，算法性能较好。R值越大，轨迹跟踪过程比较平缓，可以降低系统的误差的幅值大小。选取加权矩阵Q和R需要综合考虑LQR控制器的准确性和稳定性。因此，本文将利用遗传算法对加权矩阵Q1、Q3和R三个参数进行确定，如图4所示。

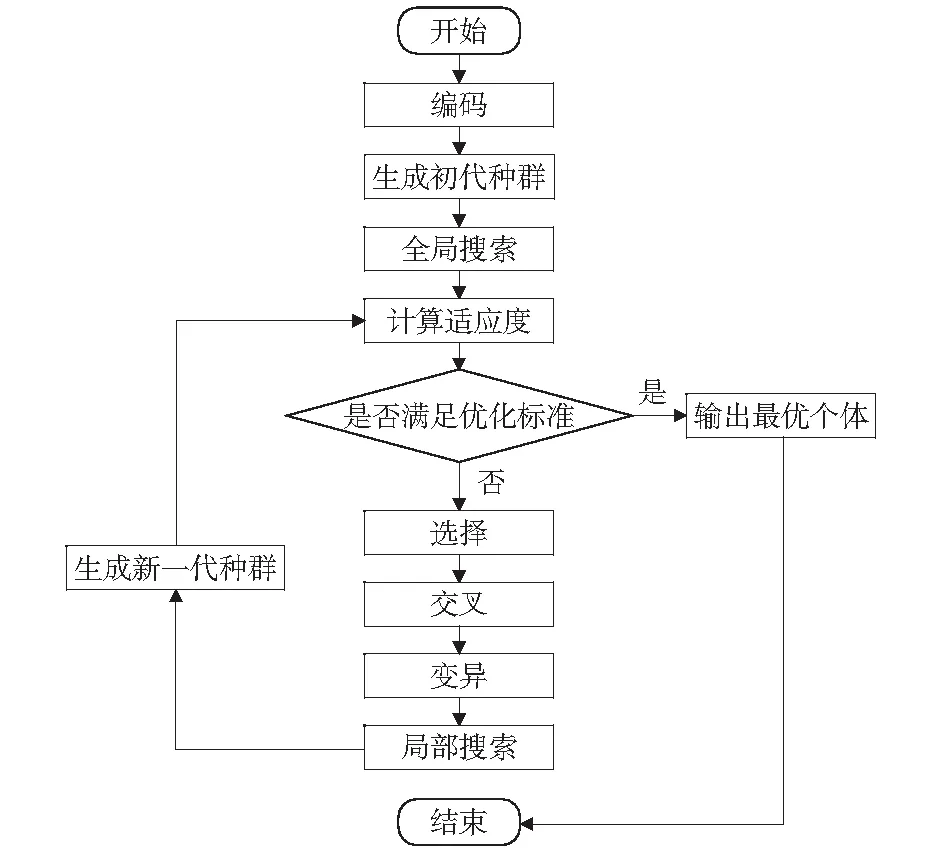
图4 遗传算法优化流程Fig.4 Genetic algorithm optimization process

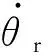
(30)

设定最大遗传次数100，原始种群的个体数设置成30，交叉概率设置成Pc=0.6，变异概率设置成Pm=0.03，起始的Q1、Q3和R分别设为15，5和20，图5所示为经GA优化的结果。并选用一段正弦曲线轨迹进行跟踪对比，如图6所示。

从图5(a)的Q1、Q3曲线与图5(b)的R优化过程可以看出，在寻优初期搜索速度较快，最终收敛于第25次迭代，最优参数值分别稳定于30、5和10，并且遗传算法优化后的LQR参数在追踪精度上与未优化相比表现的更出色。最终LQR的权重矩阵设置为：Q=diag(30,1,5,1)，R=10，控制器能准确且稳定地跟踪上目标轨迹。

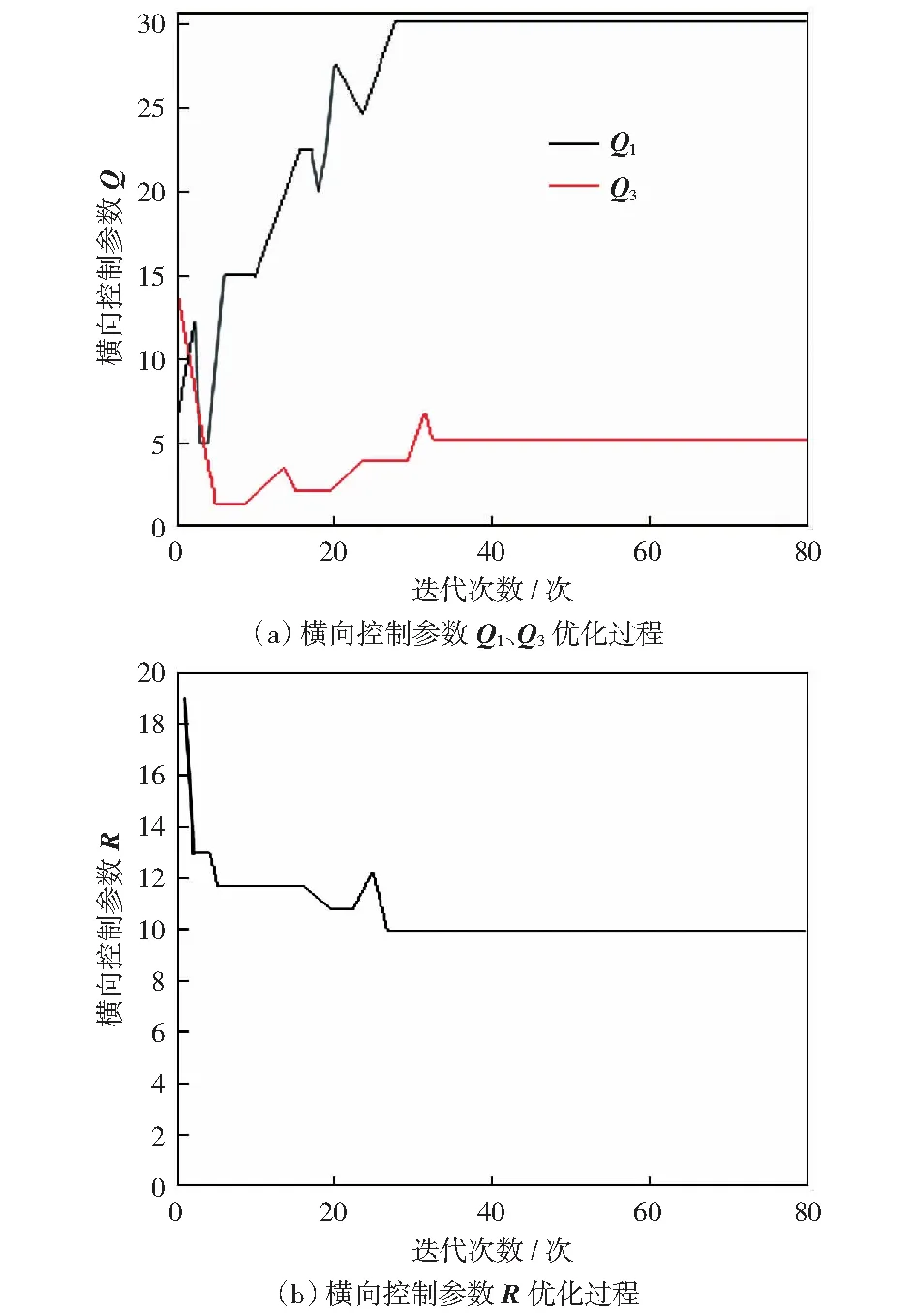
图5 经GA优化的结果Fig.5 Results optimized by genetic algorithm

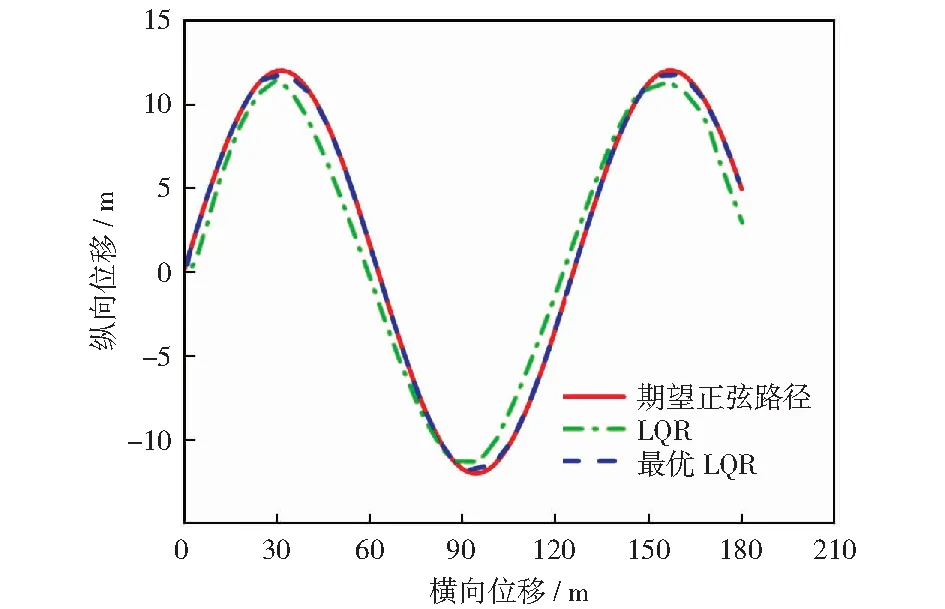
图6 路径跟踪轨迹对比Fig.6 Path tracking trajectory comparison

3.4 仿真结果分析

3种工况下的规划轨迹和跟踪轨迹、目标速度和跟踪速度、前轮转角、距离偏差、横摆角速度的仿真结果如图7所示。

在低速工况下，车辆可以跟踪规划出的期望轨迹和期望速度，跟踪效果良好，并且其距离偏差在0.04 m之内，这表明本控制器在低速工况下可以保持较高的跟踪精度。前轮转角和横摆角速度在低速情况下变化较平稳，没有出现抖动，且车辆完成泊车后能很快地收敛到稳定状态，说明控制器具有比较高的鲁棒性。

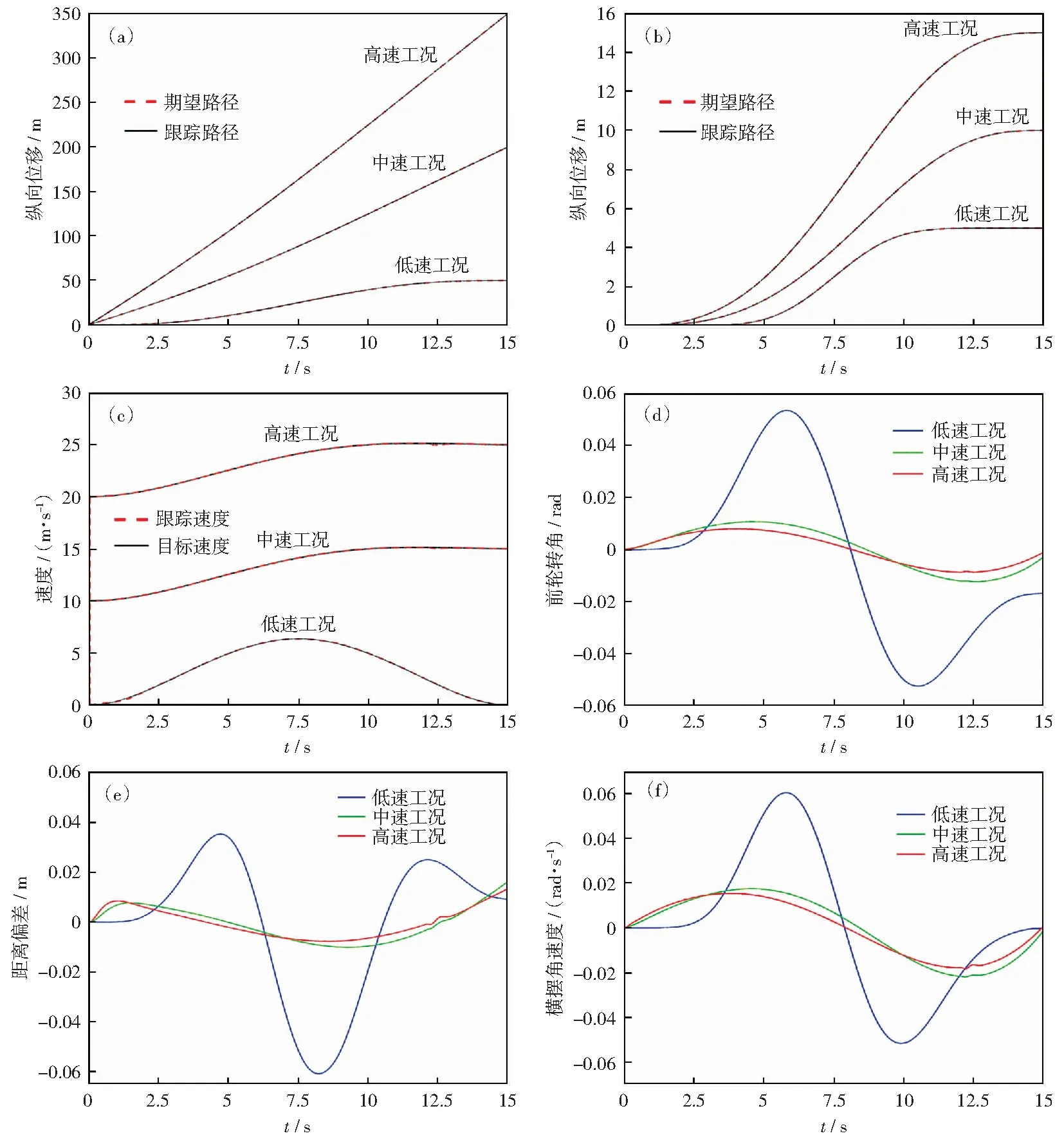
图7 路径跟踪仿真效果Fig.7 Path tracking simulation results

在中速工况下，车辆可以跟踪规划出的期望轨迹和期望速度，跟踪效果良好，并且其距离偏差在0.025 m之内，相对于低速工况来说距离偏差更小，这表明本控制器在中速工况下跟踪精度更高。前轮转角和横摆角速度相对于低速情况下减小，变化仍然较平稳，在12 s附近会有小幅度的抖动，导致跟踪速度与目标速度之间会有一些偏差，说明该控制器的鲁棒性随着速度的增加会有一定程度的降低。

在高速工况下，车辆可以跟踪规划出的期望轨迹和期望速度，跟踪效果良好，并且其距离偏差在0.02 m之内，这表明该控制器在高速工况下跟踪精度非常高。前轮转角和横摆角速度较低，可以被控制在较小的范围内，在12 s附近出现抖动现象，说明该控制器在高速工况下的鲁棒性低于低速工况。

4 结论

本文针对智能车轨迹跟踪问题，采用横纵向综合控制策略对其进行研究。为了更好地验证轨迹跟踪控制实际效果，保证轨迹跟踪的实时性，建立了车辆二自由度动力力学模型，只考虑汽车的横摆和侧向运动。在此基础上考虑距离偏差和航向偏差，得到了跟踪误差模型。轨迹跟踪控制主要是车辆的纵向速度跟踪控制和横向轨迹跟踪控制。本文通过纵向双PID控制器来调整车辆的位置误差和速度误差，进而控制车辆的驱动与制动。另外，根据期望的路径，LQR算法及前馈控制，横向控制器会生成一个合适的方向盘转角，并通过遗传算法来确定横向控制器的加权矩阵参数，从而实现一个准确的路径跟踪。在CarSim和Simulink仿真环境分别对低速泊车、中速驶入、高速驶入三种工况进行了联合仿真分析。结果表明该控制器能够完成多种工况下的联合仿真试验，跟随所给定的路径模型行驶，具有良好的控制精度和稳定性，并且保证车辆的灵活性。