A nonlinear creep damage model for gelled waxy crude

Hong-Ying Li , Qing-Bo Xie , Ho Sun , Wei Guo , Feng Yn , Qing Mio ,Cho-Fei Nie , Yu Zhung , Qin Hung , Jin-Jun Zhng

a National Engineering Laboratory for Pipeline Safety/MOE Key Laboratory of Petroleum Engineering/Beijing Key Laboratory of Urban Oil&Gas Distribution Technology/ China University of Petroleum, Beijing,102249, China

b PipeChina Pipeline R&D Center, Langfang, 065000, China

c Jinan Urban Planning and Design Institute, Jinan, 250101, China

Keywords:Waxy crude oil Rheology Yield Creep Constitutive model Mechanical analogy

ABSTRACT Yielding behaviors of waxy crude oil is one of the key issues of flow assurance challenges.The yielding of waxy crude under constant stress is actually a creep process of strain accumulation to structural failure,to describe the process completely and accurately is the basis of numerical simulation of restart process of the pipeline. The creep and yield behaviors of two gelled waxy crudes were investigated experimentally under different constant applied stresses. The results clearly show that the creep process of waxy crude is related to the applied stress and time. The greater the applied stress, and the longer the loaded time,the more obvious the nonlinear features.Based on the fractional calculus theory,a fractional viscous element was developed to describe the decelerated and steady creep process of gelled waxy crude. On the basis of the damage theory, an elastic damage element was proposed to describe the accelerated creep after the yielding. According to the idea of mechanical analogy, a nonlinear creep model was established by a fractional viscous element, an elastic damaged element, and an elastic element in series, which can accurately describe the whole creep and yielding process of gelled waxy crude.

1. Introduction

Waxy crude oil displays inferior flowability and complex rheological behaviors near and below its gelation temperature due to the wax precipitation and the wax crystal structure formation (Li and Zhang, 2003; Oliveira et al., 2012; Fakroun and Benkreira,2020), which may cause serious problems in the operation of waxy crude oil pipelines. Waxy crude oil is ordinary Newtonian fluid when the oil temperature is higher than the wax appearance temperature(WAT)since wax is completely dissolved in the liquid oil. When the temperature is below the WAT, the dissolved wax begins to precipitate out,resulting in a significance increase in the oil's viscosity. With the precipitated wax increases as temperature cools down further, and wax crystal interlocking structure progressively builds up,the crude oil gradually converts into complex non-Newtonian fluid and presents viscoelasticity (Rønningsen,1992; Chang et al., 1998; Kan′e et al., 2004; Oliveira et al., 2012;Teng and Zhang, 2013; Bao et al., 2016; Sun et al., 2016), yielding behavior (Chang et al.,1999; Davidson et al., 2004; Jia and Zhang,2012; Bai and Zhang, 2013; Li et al., 2015; Gabriel and Edson,2018) and thixotropy (Teng and Zhang, 2013; Mendes et al., 2015;Andr′es et al., 2016; Yuan et al., 2019; Mamdouh et al., 2019). Previous work has shown that about 2%precipitated wax is enough to cause oil gelling and losing flowability (Rønningsen et al., 1991;Kan′e et al.,2003; Li et al.,2005).Because the rheological property of waxy crude oil is one of the key flow assurance issues, the yielding behavior has always been a concerned research topic in petroleum industry.

Understanding and well-describing the yielding behaviors of gelled waxy crude oils is of great importance to pipeline restart analysis, and thus the yielding behavior of waxy oil has been extensively investigated. The gelled waxy crude oil can be considered as an elasto-visco-plastic material,and its yielding behavior of waxy crude oil is unlike that of common yield stress fluid.When a deformation is induced, the gelled waxy crude oil undergoes a viscoelastic creep and then structural fracture and breakdown.Wardhaugh and Boger,(1991)divided the yielding process of waxy crude oil into three successive stages: the elastic response, the creep(slow deformation),and the sudden and dramatic fracture of the structure. According to the response of strain and strain rate,some scholars separate the creep and yield process of waxy oil into the following phases:an instant elastic deformation,a decelerated creep, a steady creep (Oh et al., 2009; Hou and Zhang, 2010; Liu et al., 2018); and an accelerated creep after the above mentioned three phases when the oil yielded (Liu et al., 2018). The Burger mechanical-analogy model, which is the association in series of a Maxwell model and a Kelvin-Voigt model and has the advantages of simple constitutive equations and clear physical meaning of parameters,is usually employed to describe the creep behaviors of gels(Yilmaz et al.,2012;Sun et al.,2014).However,evidences have shown that the Burger model can describe well neither the incipience of creep nor the accelerated creep after the yielding for gelled waxy crude oil(Sun et al.,2014),since the Burger model is virtually a linear model and it could not gain better fitting results for the nonlinear creep process of waxy crude oil. Hou and Zhang (2010)experimentally investigated the creep behavior of Daqing crude oil,and put forward a mechanical analogical creep equation on the basis of analyzing the experimental data, nevertheless this model cannot depict the accelerated creep stage after the oil yielded.Since the creep and yield property of waxy crude oil directly affects the restart process of the pipeline(Zhang et al.,2013;Luiz et al.,2018;Behbood et al., 2018; Fakroun and Benkreira, 2020), a model that can describe the whole creep and yield process plays an important role in numerical simulation for restart analysis.Several models to describe the mechanical response of wax gels during yielding process have been developed by scholars. Paso et al. (2009)developed a third order degradation kinetics model to describe the time-dependent yielding process of waxy oil gel. According to rheological experiments and the Paso et al. ‘s third order model,Zhao et al. (2012 (a)) established a wax gel breakage model to depict the complete mechanical response from initial linear elastic behavior to equilibrium viscous flow, they (Zhao et al., 2012 (b))also developed a yield stress model on the basis of a modified and experimental results.Unfortunately,these models mainly focus on the yielding of the gel, a model that can describe the entire creep and yield process is still lacking for waxy crude oil.In this paper,the creep and yield behaviors of gelled waxy crude oil were investigated experimentally under different constant applied stresses.Based on the fractional calculus theory and the damage theory in solid mechanics, a nonlinear creep model was established to describe the whole creep and yield process of gelled waxy crude oil according to the idea of mechanical analogy.

2. Creep behaviors of gelled waxy crude oil

2.1. Experiments

The creep behaviors of two typical waxy crude oils were investigated by a controlled stress rheometer HAAKE RS150H(Germany) equipped with a Z38 concentric cylinder with grooves(diameter of inner bob:38 mm; length: 55 mm; ratio of radii:1.1415; gap width: 2.69 mm; 20 grooves) in the present work. For rheological measurement of suspension system, the wall slip phenomena maybe relieved when the size of surface roughness is obviously larger than size of the dispersed particles(Sanchez-Reyes and Archer, 2003; Ballesta et al., 2013). Since the size of wax particles in waxy crude oils are generally on the order of micrometers(Yi and Zhang,2011;Xue et al.,2019),the wall slip phenomena maybe mitigated by using the grooved surface geometry. Table 1 lists some properties of the two oils and the corresponding test methods.

Table 1 Waxy crude oil properties and corresponding test methods.

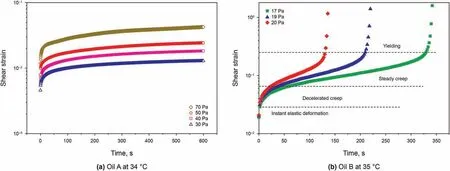
Fig.1. Creep curves of oil samples under different constant applied stresses. (a) oil A at 34 °C (b) oil B at 35 °C

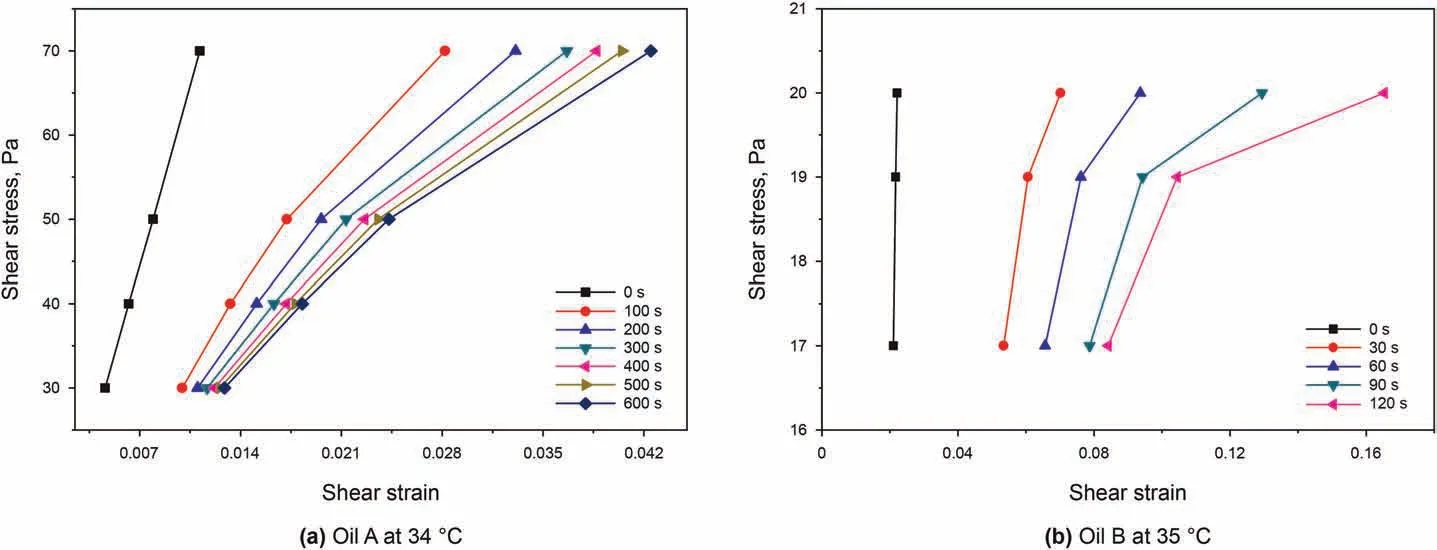
Fig. 2. Isochronous stress-strain curves at different loading time of the samples. (a) oil A at 34 °C (b) oil B at 35 °C

In order to eliminate the impact of experienced shear and thermal history on flow behaviors of waxy crude oil and improve the reliability and repeatability of the experimental results, the oil samples were pretreated through the common method before the experiments.That is,to heat the samples in seal bottles to 80°C and keep them at this temperature for 2 h, and then cool down the samples naturally to the room temperature and hold for at least 48 h (Yan and Luo,1987; Liu et al.,2018).

The creep behaviors of both oils below their gelation temperature were examined at different constant stresses.Heat pretreated oil samples to 60°C and then transfer them into the rheometer which also had been preheated to 60°C (temperature was controlled by a HAAKE AC200 water bath with accuracy of±0.1°C).Keep samples isothermally for 10 min and then cool them to the test temperatures(34°C for oil A,the corresponding amount of wax precipitation is 2.53 wt%; and 35°C for oil B, the amount of wax precipitation at this temperature is 1.42 wt%)at a rate of 0.5°C/min,and hold samples isothermally for 90 min in order to form stable waxy crystal structure before tests. After that, a constant shear stress was applied to the sample for 600 s, and the corresponding strain was recorded.Fig.1 illustrates the experiment results.Three measurements were conducted for each rheological experiment,that is, replaced a fresh specimen after each rheological experiment,and reproduced each test three times.The data from different samples of the same oil have a difference up to 20% in the results.The rheological curve presented in Fig.1 is the average value of the three tests.

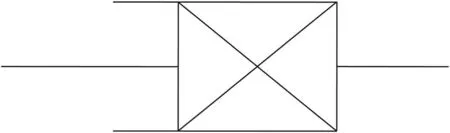
Fig. 3. Schematic of the fractional viscous element (Able dashpot).

2.2. Creep characteristics of gelled waxy crude oil

It can be seen form Fig.1 that the gelled oil A did not yield within the time scale of 600 s although the applied stress is up to 70 Pa,while the gelled oil B yielded no more than 350 s even the applied stress is only 17 Pa, which indicates that the gelled oil A has stronger inner waxy crystal structure than that of gelled oil B.When the stress is applied, an instantaneous strain is immediately observed, and the greater the applied stress, the greater the generated instantaneous strain, which indicates that the sample experiences an instantaneous elastic deformation. After the instantaneous strain, a decelerated creep can be observed before 30 s,and then a constant rate creep can be observed.For the gelled oil A, it experiences an instantaneous elastic deformation, a decelerated creep, and a steady creep (i.e. a constant rate creep)under the constant applied stress of 30-70 Pa.While for the gelled oil B, it experiences an instantaneous elastic deformation, a decelerated creep, a steady creep, and an accelerated creep (i.e. a dramatic increase in strain) after yielding under the constant applied stress of 17-20 Pa. It can be observed that the yielding of the gelled oil B appeared at the accumulated strain reaches to about 0.27, and the greater the imposed stress, the shorter the yielding time.

It is clear from Fig.1 that the applied stress directly affects the creep strain response of gelled crude oil.For the gelled oil A,when the loading stress is 30 Pa,40 Pa,50 Pa and 70 Pa,the instantaneous elastic deformation is 0.00459, 0.00593, 0.00792 and 0.01179,respectively; the creep strain at the time of 600 s is 0.01288,0.01827,0.02429 and 0.04248,respectively.These data indicate that both the instantaneous elastic strain and the strain rate increase with the increase of applied stress.

In order to easily and clearly find out the characteristics during the creep, the strain vs. time curve in Fig. 1 transformed into isochronous stress vs. strain curve, see Fig. 2. It is obvious from Fig.2 that the isochronous stress-strain curves show very different patterns at different time. At time zero, the stress-strain curve is straight, and the curvature of isochronous stress-strain curve is constant. This is because the structure of gelled oil is relatively complete at the initial moment of the creep,consequently it shows obvious linear viscoelastic characteristics after stress being applied,and the stress and deformation of oil show a linear relationship.When the time is not 0,the curvature of the isochronous stress vs.strain curve changes little at the initial stage of creep.As the creep time increases, the curvature of the isochronous stress - strain curve decreases gradually,the curve moves toward the strain axis,and the deformation modulus decreases gradually,which indicates that obvious nonlinear characteristics appear. These results show that the time is an important factor affecting the nonlinearity of the creep of gelled waxy crude oil.The longer the creep time,the more obvious the nonlinear characteristics.

3. Development of nonlinear creep damage model for gelled waxy crude oil

3.1. Fractional order viscous element

Since the Burger model is virtually a linear model, it cannot describe the nonlinear characteristics of the creep of gelled waxy crude oil.The constitutive equations of linear elements are derived based on the theory of integral order calculus, which only covers the information of the current moment. Whereas fractional calculus covers all the information from the initial moment to the current moment,which is an extension of integral order calculus,so it can more truly and effectively describe the relations between stress and deformation of materials.

There are a lot of fractional order calculus definitions, among which the Riemann Liouville theory is widely used(Miller and Ross,1993; Shakoor et al., 2012; Fernandez et al., 2019; Liang, 2019).According to the Riemann Liouville theory, the α integral of function f(t) on the integrable space [0, t] can be expressed as:

where, D is the fractional order derivative operator; t is the integration variable;τ is the stress;α(α>0)is the fractional order,and n-1<α≤n (n is a positive integer larger), and α can be fractional or plural;Γ（α） is the gamma function:

where, G is elasticity modulus. The constitutive relation of fractional viscous elements obeys Hooke's law, that is the ideal solid stress-strain relationship.

When α=1,

Eq. (4) is the ideal fluid stress-strain relationship follows Newton's law of viscosity.

When 0<α < 1, Eq. (4) describes the constitutive model a material between an ideal solid and an ideal fluid. For waxy oil, the parameter α varies as a function of temperature and time because the structure of wax particles differs with temperature and stress loading time.

According to the Riemann Liouville fractional calculus theory(Miller and Ross,1993; Shakoor et al., 2012), it can be obtained by the fractional integration of both sides of Eq. (4):

Eq. (7) is the constitutive equation of a fractional order viscous element. A fractional order viscous element may present the mechanical change process of the viscoelasticity of a material.During the creep,the strain of a fractional order viscous element is neither constant as that of an ideal solid, nor steady increase as that of an ideal liquid.In the case of the stress remaining constant,the strain increases slowly,and the creep rate decreases with time and finally trends to be a constant.Under the condition of constant strain,the stress neither remains unchanged nor rapidly decreases to 0. The decelerated creep and steady creep of gelled waxy crude oil is such a process. In consequence, the nonlinear creep process before yielding of gelled waxy crude oil can be well described by a fractional order viscous element expressed by Eq. (7).

The fractional differential order α in Eq. (7) represents the tendency of viscoelasticity, it can control both the creep rate and deformation value during the creep process. When α is smaller,both creep and creep rate are small. With the increase of α, both creep and creep rate increase at the same time. The viscosity coefficient ηαexhibits the similar properties like that of the fractional differential order α.

In summary, a fractional order viscous element can not only control the creep rate of materials but also the strain value,while an integer order viscous element can only govern the creep rate of materials through the viscosity coefficient. Therefore, fractional order viscous element has more advantages than integral order viscous element in describing the nonlinear creep process of materials.

3.2. Elastic damage element

There are two major methods to model the accelerated creep stage, one is by viscosity coefficient, and the other is establishing damaged elements based on damage mechanics. The former method is to develop viscoplastic elements whose viscosity coefficient decreases nonlinearly with applied stress and time. However, this method can only fit the creep curve and cannot explain the accelerated creep mechanism of materials.The latter method of establishing damaged elements is to introduce damage variables to modify the creep parameters of materials based on the principle of structural damage evolution,and combine damaged elements with other traditional elements to describe the whole creep and yield process of materials.Actually,the creep and yield process of gelled waxy crude oil can be regarded as a process that the structure of oil resistance to deformation and destruction gradually deteriorates,and results in damage and failure. By referencing the material damage theory, damaged element is introduced to describe the accelerated creep of gelled waxy crude oil.

“Damage”is a concept in the solid mechanics,which means that the overall structural strength of a material is irreversibly weakened due to the continuous expanding of pores, cracks and other microstructural defects under applied stress. In the classical damage mechanics, damage degree of a material is measured by damage variables (Ren′e et al., 2012). The damage variable was defined as Eq. (8):

This method is assumed for the sake of convenience, but it is inconvenient for measurement. Therefore, on the basis of strain equivalence principle, a method to define damage variable by elastic modulus is derived. The strain equivalence hypothesis is proposed by Lemaitre and Chaboche (Mattias and Matti, 2005;Yang et al.,2010).It is assumed that the deformation of a damaged material when stress applied is equivalent to the deformation generated by the stress when the material is not damaged.The load area of the undamaged material is equal to the actual effective load area of the damaged material. That is:

Thus, Eq. (9) can be expressed as:

Fig. 4. Creep curves of damage element at different C (τ = 17 Pa, G0 = 8000 Pa,m = -0.3192).

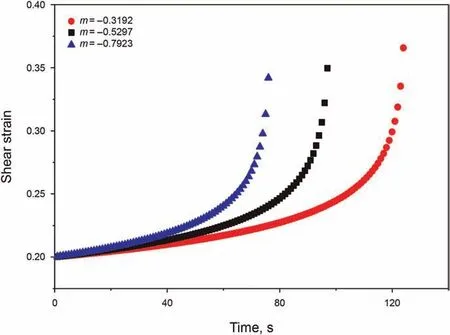
Fig. 5. Creep curves of damage element at different m (τ = 17 Pa, G0 = 8000 Pa,C = 0.0217).

For a gelled waxy crude oil without structure damage, its mechanical properties can be described by an elastomer element,and its constitutive equation can be expressed:

Fig. 6. Nonlinear damage creep model.

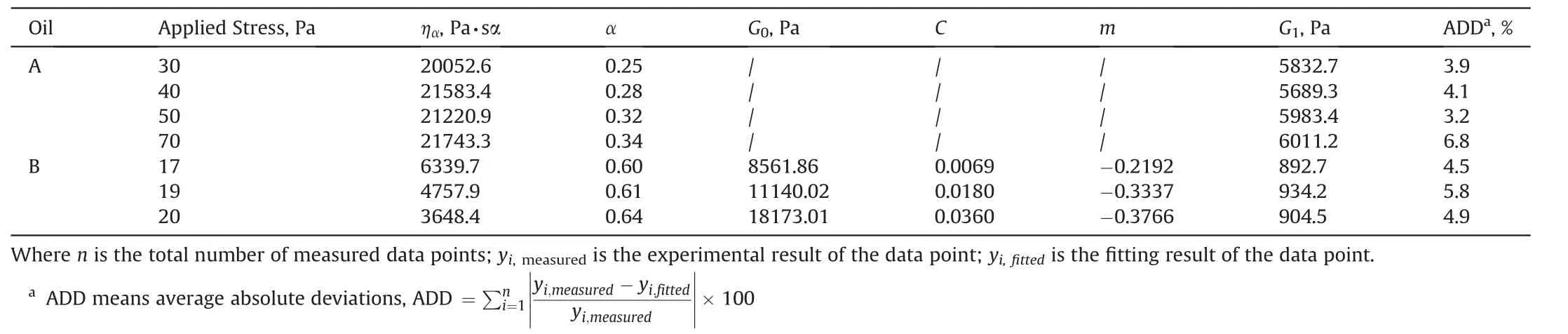
Table 2 Parameters of the nonlinear creep damage model (Eq. (23))for gelled waxy crude oils.

where the creep damage time tycontains the influence of the stress on the gelled oil.

Fig. 7. Comparisons of creep curves between experimental data and model fitting results.(a) oil A at 34 °C (b) oil B at 35 °C

Table 3 The fitted parameters of Eq. (23) for a waxy oil reported in a literature(Huang et al., 2021).

Fig. 8. Comparisons of creep curves between experimental data and model fitting results.

From Eq. (18) and Eq. (19), we can obtain:m. Fig. 4 shows that the creep rate of elastic damaged element increases at the same time with the increase of C.Fig.5 illustrates that the occurrence time of accelerated creep shorten with the increase of the absolute value m. Higher values of C and m (absolute value)mean that the material yields more easily.

Therefore, Eq. (22) can not only reflect the initial elastic strain and accelerated creep phase,but also display the damage situation under different applied stresses and load time of material.

3.3. Nonlinear creep damage model

From the above results, it is clear that fractional order viscous element can describe the decelerated and steady creep process of a material, and the elastic damage element can depict the initial elastic strain and accelerated creep phase after yielding.In order to describe the whole creep and yield process of gelled waxy crude oil,a nonlinear damage creep model was established according to the superposition principle.

It should be note that the initial structural strength of gelled waxy crude oil is far less than that of typical solid materials although gelled oil exhibits some mechanical behaviors of solids.When applying damage element to describe the creep process of gelled oil,the initial elastic strain is so small that it can be ignored.Thus, the plastic characteristics of damage element are mainly concerned, and the initial elastic strain is represented by connecting ordinary spring element in series.In order to describe the whole creep and yield process of gelled waxy crude oil,a fractional viscous element,a damaged element,and an elastic element are connected in series according to the superposition principle(see Fig.6).Then it can be obtained:

It should be pointed out that Eq.(23)is applicable for discussing the elasto-visco-plastic behavior of waxy oil under constant stress loading conditions since it is established on the basis of analysis of creep and yielding behaviors of gelled waxy oil under constant stress.

4. Validation of the model

4.1. Verification with the experiment data

In order to verify the efficiency of the model, i.e. Eq. (23), the fitted parameters for the two gelled waxy crude oils in Fig.1 were determined by using Levenberg-Marquardt optimization algorithm of 1 stopt software,which are listed in Table 2.

It is obvious from Table 2 that the values of the initial structural strength G1for the same oil sample at different applied stress have little difference since all the specimen for the same oil experienced the same thermal and shear history and the same gel structural strength were formed.Since the waxy crystal structure yields more easily at higher applied stress, the absolute value of both parameters C and m are higher with the increasing of applied stress.

Based on the model parameters in Table 2, numerical calculations were carried out in comparison with the experimental data,which were shown in Fig. 7. The comparison between the experimental data and the numerical calculations of the proposed model reveals the numerical prediction using the nonlinear creep damage model agree very well with the creep and yield experimental results of gelled waxy crude oil. Therefore, the proposed nonlinear creep damage model is valid and reasonable,which can be used to describe the complete time-dependent and stress dependent creep and yield behavior of gelled waxy crude oil.

4.2. Verification with published data in literatures

Some published data (Huang et al., 2021), which cover a complete range from below to yield stress to above the yield stress,were used to verify the model further.The fitted parameters of Eq.(23) are listed in Table 3, and the comparison between the experimental data and the numerical calculations of Eq. (23) are illustrated in Fig. 8.

The fitted parameters in Table 3 shows again that the values of the initial structural strength G1vary little at different applied stress, which indicating that the specimen for the same oil experienced the same thermal and shear history have the same gel structural strength. Since G1represents the initial structural strength of crude oil, it can be inferred that the value of G1should be equal to the storage module in the viscoelastic linear region.From the work of Huang et al. (2021), it can be found that the storage module of the gelled oil in the viscoelastic linear region is 27514.8 Pa,while the fitting values of G1in Table 3 are in agreement with this result.

With the increase of the applied stress,the time for gelled oil to enter the accelerated creep stage is advanced, and the creep velocity increases, which results in the absolute value of both parameters C and m increase with the increase of applied stress.

The comparisons in Fig. 8 again show that the proposed nonlinear creep damage model can describe the complete timedependent and stress dependent creep and yield behavior of gelled waxy crude oil,however,how to obtain some parameters in the model from some independent experiments and then use the model to solve some problems still have a way to go.

5. Conclusions

(1) The creep experiments of gelled waxy crude oil under constant applied stress show that the creep process of waxy crude oil is related to the applied stress and time.The greater the applied stress,and the longer the loaded time,the more obvious the nonlinear features.(2) Based on the fractional calculus theory, a fractional viscous element was applied to describe the decelerated and steady creep process of gelled waxy crude oil. On the basis of the damage theory in solid mechanics, an elastic damage element was developed, which can describe the accelerated creep of gelled waxy crude oil after the yielding.(3) According to the idea of mechanical analogy, a nonlinear creep model was established by a fractional viscous element,a damaged element in series, and an elastic element, which can accurately describe the whole creep and yield process of gelled waxy crude oil.(4) The comparison between numerical calculations of the pro

posed nonlinear creep model and the experimental data shows that the proposed model may describe well the complete creep and yield behavior of gelled waxy crude oil.

Acknowledgement

The authors acknowledge the financial support from the National Natural Science Foundation of China (No.52174066).