四旋翼飞行器飞行姿态的自抗扰控制研究

陈昊晟

（华北水利水电大学，河南郑州，450045）

0 引言

四旋翼飞行器由四个对称的电机和螺旋桨构成，其通过对四个动力组旋翼转速的调节完成垂直起降、水平飞行、悬停、俯仰、偏航等一系列动作[1]。近年来，因为四旋翼飞行器具有飞行平稳、机动性能卓越、维护成本较低、易微型化等优点，已在军事和生活等多个领域得到了广泛应用。

四旋翼飞行器具有非线性、强耦合、多变量的特点，是一种四输入六状态输出的欠驱动系统[2]，然而飞行器控制系统易受各种外界因素的干扰，如：本身载荷、形状大小、模型准确性等。故推出四旋翼飞行器在具有不确定干扰情况下的稳定控制系统是研究其姿态控制问题的重点。国际上对其姿态控制器进行了一定的深入研究，主要的控制方法有经典PID算法、自适应控制、反步法、滑模控制等。但PID控制调节时间长，不容易满足高性能要求；自适应控制、反步法、滑模控制属于非线性控制，对模型的精确度要求比较高，而模型参数的获取由于各种因素的干扰不可避免地会存在误差，在实际应用的过程中，控制性能和抗干扰效果均有一定的减弱。

文献[3]采用一种基于自耦PID控制器的四旋翼飞行器姿态回路控制方法。文献[4]提出了一种基于自适应反步法的补偿控制策略，所设计的控制器即使在集总干扰存在的情况下，也能保证跟踪误差的瞬态性能。文献[5]设计了一种内外环控制算法，内环采用自抗扰控制器，外环采用非奇异终端滑模控制器提高系统的响应速度。文献[6]利用有限时间控制理论，提出了一种四旋翼飞行器快速姿态跟踪控制算法，可以在有限时间内达到预期姿态。

本文为有效地提高飞行器对外界不确定干扰因素的适应能力，建立了关于四旋翼飞行器的简化动力学模型，采用一种基于自抗扰控制的四旋翼飞行器姿态控制方法，在控制过程中通过产生所期望的姿态角度，进而达到姿态控制这一目的，研究设计得到的自抗扰控制算法对于四旋翼飞行器姿态的控制具有不依赖于模型参数精度和较强的鲁棒性、稳定性等优点，能对飞行器进行精确实时控制。最终通过仿真实验结果验证了本文控制方法的有效性。

1 四旋翼飞行器动力学模型的建立

四旋翼飞行器一般有两种模式，分别为“十”字形模式和X形模式[7]，本文以X形模式飞行器为例进行分析。

首先，为了获得四旋翼飞行器控制系统的数学模型，分别建立惯性坐标系E[OXYZ]和机体坐标系B[oxyz],如图1所示。定义ψ、θ、φ分别为偏航角、俯仰角、滚转角[8]，m为四旋翼机体的质量，g为重力加速度，c为升力系数，d为反扭矩系数，ωj(j=1、2、3、4)为第j个螺旋桨的转速，U为四旋翼飞行器产生的总升力，Ux、Uy、Uz分别为飞行器在x、y、z轴上所受到的力矩，Ix、Iy、Iz对应飞行器绕x、y、z三个坐标轴的转动惯量,L为旋翼中心到机体质心的距离。

图1 四旋翼飞行器的坐标系

为了简化模型，假设四旋翼飞行器为质量不变且重心不发生变化的刚体，在室内或室外无风及慢速飞行的条件下，忽略阻力等其他外界干扰。基于上述假设条件，利用牛顿第二定律和欧拉方程可得出小角度姿态变化情况下四旋翼飞行器的动力学数学模型为：

其中：

2 自抗扰控制器研究

观察四旋翼飞行器的数学模型可知，无法得到一个四旋翼的精确数学模型。其姿态控制系统关于运动模型的参数存在不确定性，为有效提升四旋翼飞行姿态的稳定控制，本文采用自抗扰技术设计四旋翼飞行姿态的跟踪控制器。

自抗扰控制技术不依赖被控对象的精确模型，把所有作用于被控对象的不确定外扰因素作用都归结为未知扰动，并用对象的输入输出数据对其进行估计和补偿，在要求实现高速高精度的场合能很好地体现其优越的控制性能，自抗扰控制器主要包括以下三个部分：跟踪微分器（TD）、非线性状态误差反馈律（NLSEF)、扩张状态观测器（ESO）[9]，其结构框图如图2所示。

图2 自抗扰控制器结构图

TD根据设定值来安排过渡过程，提取被控对象的微分信号，在提取微分的同时，也尽可能地减少运算过程中引入的噪声，这样有利于得到较高精度的微分信号；ESO实时估计被控对象的状态和作用于系统的总和扰动；NLSEF结合扰动估计量的补偿来生成最终的控制信号。

在对控制器进行参数整定时，可将TD、NLSEF、ESO看作三个独立的部分，分别设计完后再组合成完整的自抗扰控制器[10]。

2.1 跟踪微分器（TD）

其中r为速度因子，决定着跟踪的快慢；h为滤波因子，决定着对噪声的滤波效果；fst函数为最速控制综合函数，表达形式如下：

2.2 扩张状态观测器(ESO)

其中b0为补偿因子，决定着系统总扰动补偿量的大小。

2.3 非线性状态误差反馈律(NLSEF)

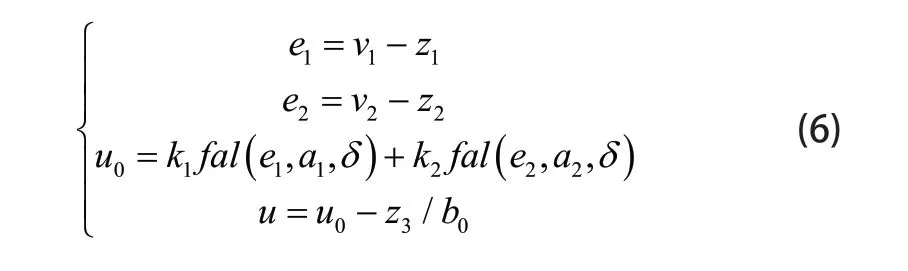
其中k1和k2相当于传统PID控制中的比例增益和微分增益，fal函数表达形式如下：

在自抗扰控制器的参数整定过程中，先整定跟踪微分器和扩张状态观测器的参数。跟踪微分器中的参数r数值越大，过渡过程越短,h越大，对噪声滤波效果越好，但二者也不能取的过大，需取值合理才能得到合适的过渡过程与微分信号；扩张状态观测器是自抗扰控制器的核心部分，这部分参数整定的好坏很大程度上决定着控制器的性能，它的跟踪精度越高，自抗扰控制器的控制性能越好。在取得一定的效果后，再结合非线性状态误差反馈的性能对自抗扰控制器进行整体的参数整定。经过多次的参数整定，最终确定的参数取值如表1所示。

表1 自抗扰控制器仿真参数取值表

NLSEF a1 0.5 0.5 0.5 a2 0.05 0.05 0.05 k1 25 20 20 k2 240 200 200 δ 1 3 3

3 仿真与验证

设置四旋翼飞行器系统的仿真参数为：m=0.85kg, Ix=0.055kg·m2, Iy=0.055kg·m2, Iz=0.11kg·m2, L=0.21m。根据已经建立的四旋翼飞行器动力学模型和设计好的自抗扰控制器，在MATLAB软件中进行四旋翼飞行器飞行姿态控制的仿真实验，测试控制器的性能。将四旋翼飞行器系统分为偏航、俯仰、滚转3个通道，从而分别进行调节各个螺旋桨电机的转速达到控制四旋翼飞行器系统的目的，整个模型的结构如图3所示。

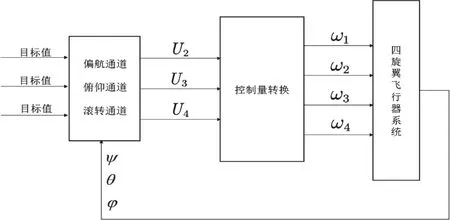
图3 四旋翼飞行姿态控制整体框图

在Simulink中进行仿真得到姿态控制效果，其中偏航角、俯仰角、滚转角的变化分别如图4所示。

图4 四旋翼飞行姿态角控制响应曲线

4 结束语

本文以四旋翼飞行器作为研究对象，对其在数学上建立了动力学模型，设计了一种基于自抗扰控制研究的控制器，从仿真结果上看，飞行器的偏航角、俯仰角、滚转角均能较快地对目标姿态位置产生跟踪响应，稳态误差几乎为零，验证了控制器具有良好的鲁棒性和稳定性。自抗扰控制器的设计克服了实际中难以建立精确被控模型的困难，无需得到精确的四旋翼飞行器被控模型就能够达到控制目的，并且实时补偿系统扰动，有效提高了飞行器的响应速度及目标姿态角的跟踪精度，工程应用价值较大。