基于RANS方程的共轴刚性旋翼气动干扰参数影响分析
2021-06-17李春华
田 波,李春华
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
常规单旋翼构型直升机受前行桨叶动态失速和后行桨叶气流分离的影响,其高速飞行能力被限制。共轴刚性旋翼构型直升机通过上下反向旋转的旋翼抵消反扭矩;在大速度前飞时,降低旋翼转速限制桨尖马赫数,旋翼只提供升力,由辅助推进装置产生推力克服前飞阻力;同时基于前行桨叶概念,对后行侧桨叶卸载,充分发挥前行侧桨叶升力潜能,提高气动效率。该构型直升机兼具悬停和高速前飞能力,具有机动性强、气动性能优越、操纵性好、结构紧凑等特点。共轴刚性旋翼作为直升机的关键部件,独特的结构特点和运转模式使其气动环境比常规旋翼更为复杂,即使在悬停状态旋翼流场也呈现高度非定常特性。其气动性能对直升机的飞行性能、操纵性和稳定性至关重要。为充分了解共轴刚性旋翼技术并掌握使用,为高速直升机发展提供支持,开展共轴刚性旋翼气动干扰分析意义重大。
国内外针对共轴刚性旋翼气动干扰特性开展了一系列研究。在理论分析方面,Leishman在单旋翼动量/叶素理论基础上引入诱导速度干扰因子,基于动量方程建立了共轴双旋翼的品质因数表达式;Schmaus J H基于升力线模型和自由尾迹研究了共轴刚性旋翼高速飞行时的气动特性,分析了气动干扰和升力偏置对旋翼气动效率的影响;黄水林等计入三维桨尖效应建立了适用于共轴双旋翼流场特性分析的自由尾迹模型。随着技术发展,计算流体力学(Computational Fluid Dynamics,简称CFD)在共轴双旋翼气动特性计算中得到应用。Ruzicka建立了基于RANS方程的共轴双旋翼流场求解方法;美国NASA Ames研究中心通过高精度CFD分析模型对高速前飞状态下共轴刚性旋翼流场的复杂流动特征和旋翼附着涡、尾迹涡和脱体涡的相互干扰现象进行了研究;许和勇采用非结构重叠网格求解Euler方程,分析了悬停和前飞状态下共轴双旋翼的气动特性;朱正对共轴刚性旋翼悬停流场进行了模拟计算,对旋翼气动特性和干扰机理进行研究。目前针对共轴刚性旋翼的研究较少开展气动干扰参数影响分析,对共轴刚性旋翼非定常流场气动特性、桨涡干扰特性和载荷特性的分析还不够深入。
鉴于此,本文采用旋翼配平作为计算输入,通过运动嵌套网格计入桨叶复杂运动,以RANS方程为控制方程建立适用于共轴刚性旋翼非定常流场求解的数值模拟方法,并结合试验数据对比验证方法的准确性。在此基础上对共轴刚性旋翼悬停和前飞流场进行模拟,深入分析旋翼气动特性和干扰机理,并研究旋翼间距、相遇方位角对共轴刚性旋翼气动特性的影响。
1 计算方法
1.1 计算网格模型
为了满足高速直升机的特殊性能要求,本文计算的旋翼桨叶采用非常规的气动布局,如图1。桨根采用双钝头翼型配置,缓解根部反流区影响;桨叶根部正扭转,中段和尖部负扭转分布,弦长为非线性分布,提高旋翼气动效率;桨尖线性尖削,有效削弱桨尖涡,降低旋翼阻力距。共轴刚性旋翼参数如表1。
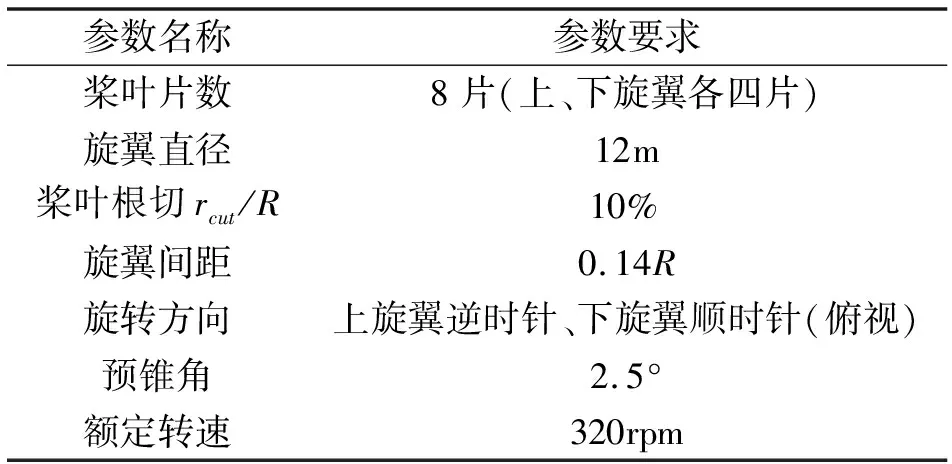
表1 共轴刚性旋翼计算参数
桨叶网格采用贴体正交结构网格,在桨尖位置和桨叶前后缘进行加密处理,准确模拟复杂三维非定常绕流产生的涡流动特征。为提高旋翼流场模拟精度,对背景网格进行局部加密,保证旋翼网格与背景网格的嵌套区域信息交换的精度。采用洞单元识别和贡献单元搜索策略对网格进行标记,实现桨叶网格和背景网格的信息插值,并随桨叶运动不断迭代交换。旋翼计算网格如图1所示。
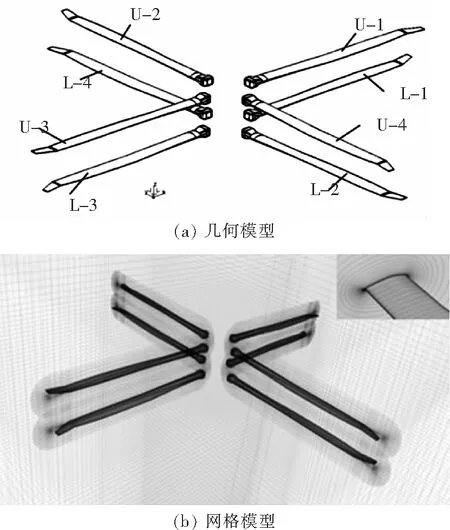
图1 计算网格模型
为了便于下文分析,对桨叶单独命名,U代表上旋翼,L代表下旋翼,1号桨叶指向来流方向,2号对应前行侧桨叶,3号桨叶指向来流反方向,4号桨叶为后行侧桨叶。
1.2 数值模拟方法
针对共轴刚性旋翼非定常流场,在惯性坐标系下定义计算坐标轴,以绝对物理量为参数建立守恒积分形式的雷诺平均Navier-Stokes方程如下:
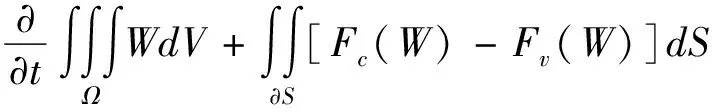
(1)
其中守恒变量W
、无粘通量F
(W
)和粘性通量F
(W
)表达如下: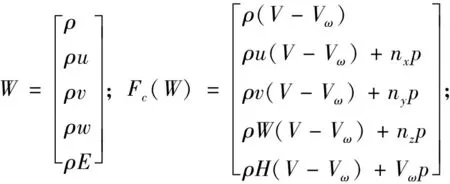
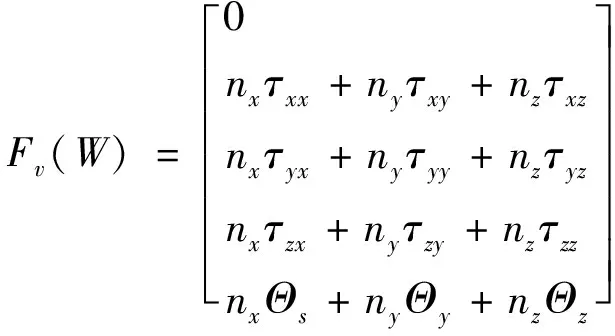
(2)
旋翼干扰流场的模拟精度很大程度上受对流通量求解精度的影响。本文采用Roe-MUSCL空间离散格式对网格面上的无粘通量进行计算,粘性通量采用二阶中心差分进行空间离散;为了准确模拟共轴刚性旋翼非定常流场,采用双时间方法(Dual time step)进行时间步进,在伪时间上采用LU-SGS格式进行推进直至完全收敛;湍流模型采用由Menter提出的k
-ω
SST二方程湍流模型更好地捕捉桨叶附面层内流动;同时采用基于Gauss-Seidel迭代的多重网格技术加快计算收敛。1.3 算例验证
以Caradonna& Tung(C-T)旋翼和Harrington Rotor 2共轴双旋翼为例,验证本文采用方法的准确性。图2给出了C-T旋翼无升力前飞状态,90°和270°方位角下桨叶0.89R
剖面的压力系数与试验值的对比。由图中可以看出计算结果与试验值吻合良好,说明采用的数值方法能够准确开展旋翼前飞流场数值模拟。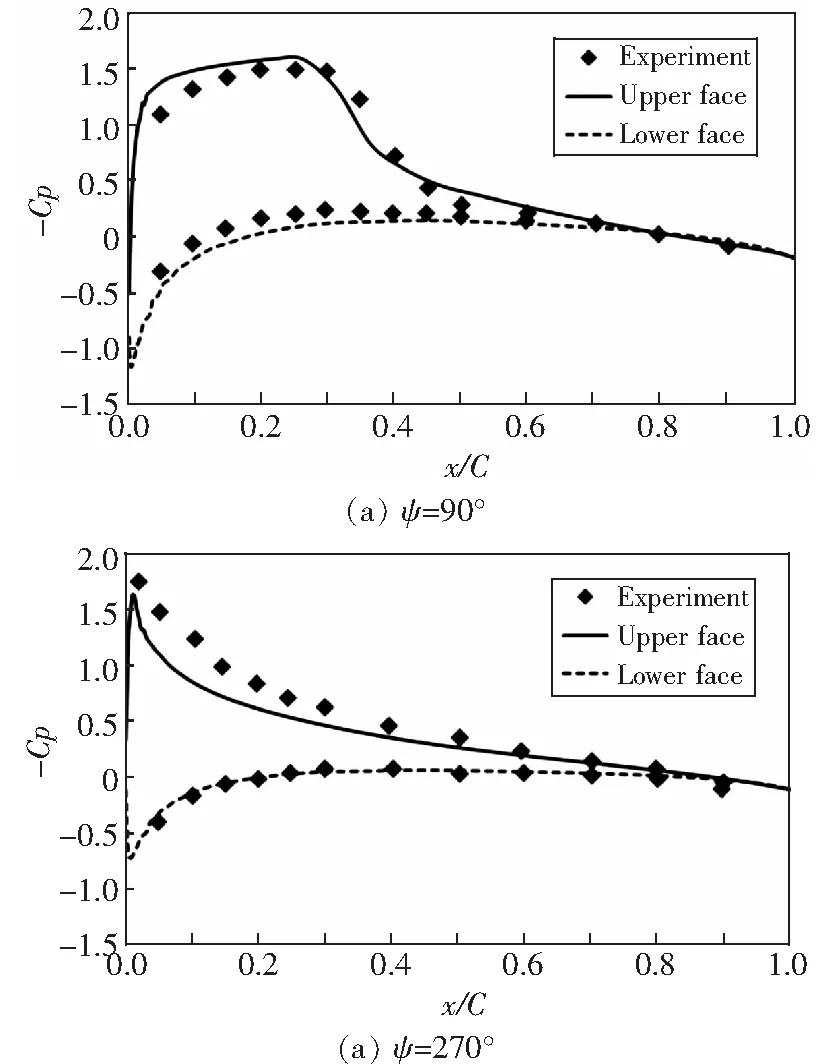
图2 C-T旋翼计算结果与试验值对比
图3给出了Harrington Rotor 2共轴双旋翼悬停状态拉力系数和功率系数曲线与试验值的对比。旋翼采用差动总距的方法进行旋翼配平,差动量为1°。计算结果与试验值有较好的吻合度,表明本文建立方法可以准确模拟共轴刚性旋翼非定常流场,进行共轴刚性旋翼气动特性计算。
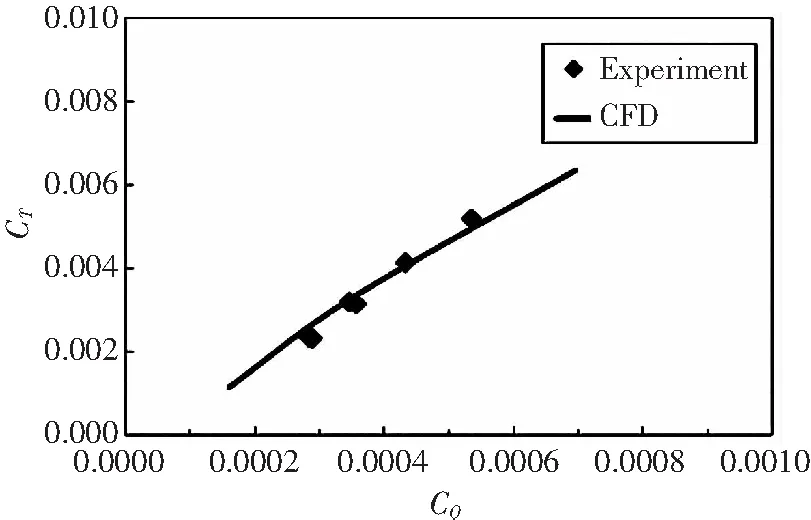
图3 Harrington 2旋翼计算结果与试验值对比
2 计算结果分析
2.1 悬停状态共轴刚性旋翼气动干扰特性
配平目标拉力系数0.025,上旋翼总距10.7°,下旋翼总距11.5°。图4给出了共轴刚性旋翼悬停状态瞬时拉力系数。由图中可以看出,旋翼拉力随方位角呈周期性变化,变化频率为8/rev。旋翼从0°方位角开始,每隔45°周期性相遇,一个周期内旋翼拉力均表现为先升高再降低。这是由于上下旋翼桨叶接近时,桨叶前缘附着涡会对另一片桨叶产生上洗作用,使上下旋翼桨叶有效迎角增大,拉力上升。由相遇转为远离时,桨叶前缘附着涡引起的上洗作用逐渐转变为桨叶后缘附着涡的下洗作用,旋翼桨叶相对迎角变小,桨叶气动力同步变化。这种周期性拉力波动现象与桨叶载荷引起的边界环量有关,也被称为“载荷效应”。
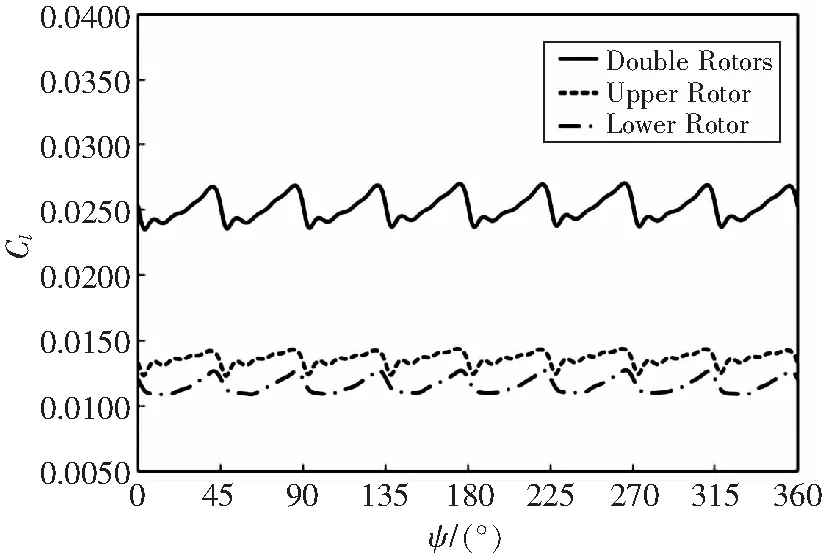
图4 悬停状态共轴刚性旋翼瞬时拉力系数
同时,旋翼拉力在桨叶相遇时出现脉冲波动。为了更直观地观察这种现象,图5给出了无升力状态共轴刚性旋翼上下桨叶的瞬时拉力系数。相遇时上旋翼桨叶拉力出现负向脉冲,下旋翼拉力正向脉冲。这是由于相遇时上下旋翼桨叶附近气流环境发生变化,流场空间受到排挤导致流管截面收缩;根据伯努利原理,流速加快,流体产生的压强就减小,上旋翼桨叶上下表面压力差减小导致拉力产生负向脉冲波动。这种现象的产生主要是因为桨叶厚度挤压流体,故也称为“厚度效应”。
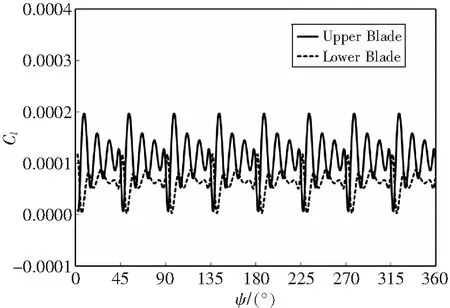
图5 无升力状态共轴刚性旋翼瞬时拉力系数
图6给出了悬停状态上下旋翼桨尖平面涡量图。共轴刚性旋翼干扰流场中,下旋翼气动干扰比上旋翼更为强烈,不仅存在与自身桨尖涡的气动干扰,与上旋翼畸变的桨尖涡也会发生涡面干扰,旋翼桨根位置受到上旋翼桨根下洗干扰。
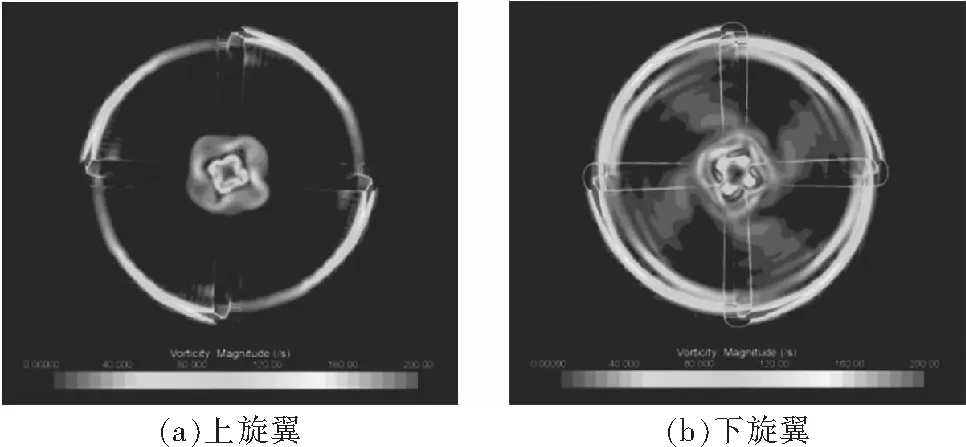
图6 共轴刚性旋翼桨尖平面涡量图
由于悬停状态下共轴刚性旋翼气动干扰最为强烈,选取悬停状态上下旋翼间距0.12R
、0.14R
、0.16R
和0.18R
进行对比计算,上下旋翼拉力系数和悬停效率随旋翼间距的变化如图7。随着旋翼间距增大,上旋翼拉力系数和悬停效率逐渐增大,下旋翼则无明显变化。这是由于下旋翼对上旋翼的诱导干扰随着间距的增大而减弱;而下旋翼受上旋翼下洗流干扰随旋翼间距的变化并不明显,故气动特性无明显波动。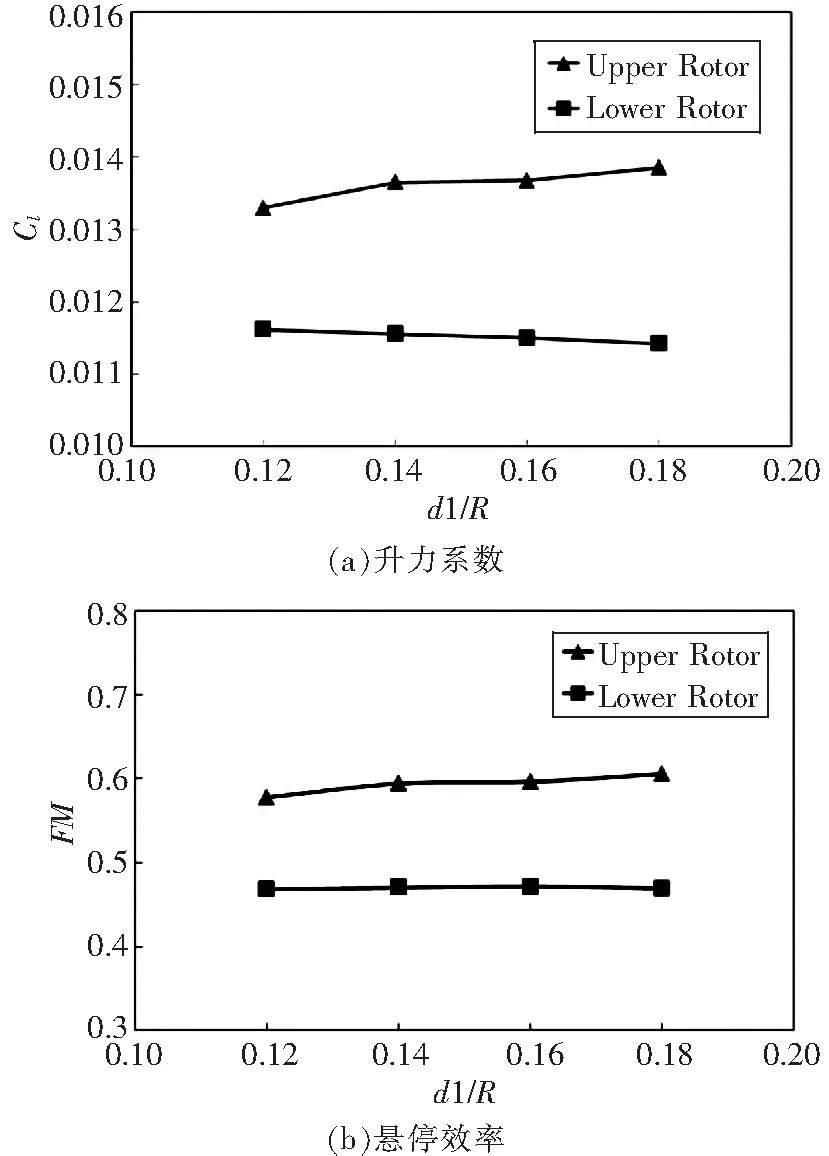
图7 旋翼间距对升力系数和悬停效率的影响
2.2 前飞状态共轴刚性旋翼气动干扰特性
以前进比0.285,拉力系数0.025为计算状态,研究共轴刚性旋翼前飞气动特性。旋翼配平数据:
上旋翼总距:θ
=5.94+3.63cosφ
-4.70sinφ
下旋翼总距:θ
=5.93+3.82cosφ
-4.60sinφ
计算得到旋翼升力系数和扭矩系数见表2。当前计算状态,上下旋翼时均拉力基本相同。图8给了出共轴刚性旋翼瞬时拉力系数,旋翼拉力波动周期为4/Rev,上下旋翼拉力波动趋向一致,较悬停状态旋翼间气动干扰减弱。
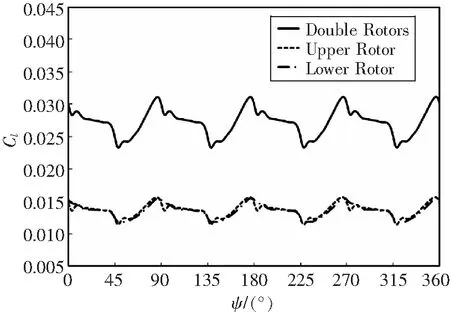
图8 前飞状态共轴刚性旋翼瞬时拉力系数
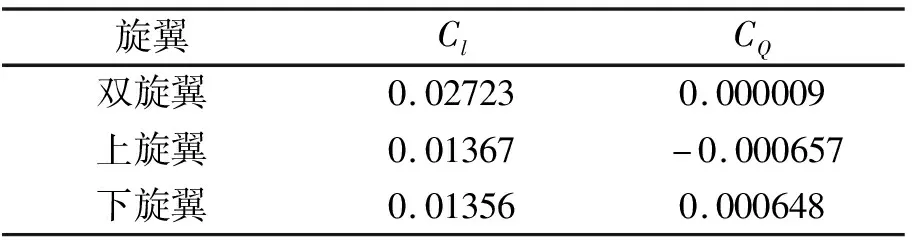
表2 共轴刚性旋翼升力系数与扭矩系数
图9给出了上下旋翼桨叶的瞬时拉力系数。U-1桨叶拉力在0°到90°方位角达到最大,在180°到270°拉力最小,各片桨叶拉力存在1/4周期相位差。计算结果符合“前行桨叶概念”,在前行桨叶附近时剖面来流速度和迎角均达到最大,产生较大升力。后行侧桨叶在前飞过程中气体来流速度较小,在大速度前飞时大部分区域位于反流区内。为了减小前飞时后行侧桨叶产生的阻力和负升力,通过变距操控减小后行侧桨叶迎角,在后行侧产生的升力较小。
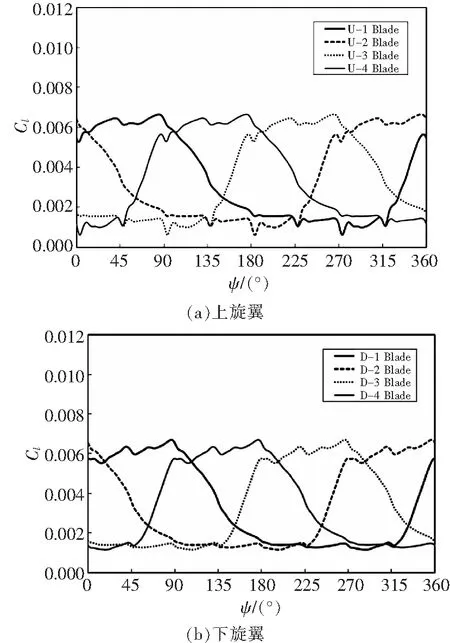
图9 共轴刚性旋翼桨叶瞬时拉力
图10给出了拉力系数0.025下不同前进比旋翼升阻比和升力偏置量(升力偏置量LOS
=C
/C
,C
为旋翼滚转力矩)。前进比0.65时旋翼转速降为额定转速的90%(该前进比计算采用降转速后的桨尖速度)。共轴刚性旋翼升阻比随前进比增大而增大,增大到一定值后增长速率减缓,然后开始下降;升力偏置量随速度增大而增大,小速度前飞时下旋翼受上旋翼的气动干扰强烈导致拉力降低,升力偏置量较小。大的升力偏置使得前行桨叶更容易发生激波附面层干扰诱导桨叶表面气流分离;偏置量较小时,会缓解桨叶气流分离在弦向和展向的分布,降低功耗,提高旋翼效率。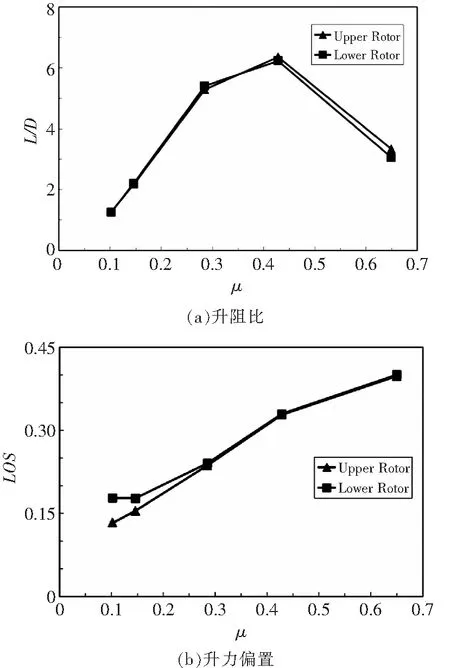
图10 共轴刚性旋翼升阻比与升力偏置
共轴刚性旋翼周期性相遇过程中受到“载荷效应”和“厚度效应”影响,导致拉力波动。改变旋翼旋转过程中的相遇角对旋翼气动干扰特性会产生一定影响。对前进比0.285,上下旋翼初始相遇角为0°、7.5°、15°和22.5°的状态分别进行计算模拟。
图11给出不同相遇角的共轴刚性旋翼瞬时拉力系数。随相遇角增大,旋翼拉力幅值降低,拉力波动减缓。在相遇角22.5°时共轴刚性旋翼拉力变化周期从4/Rev变为8/Rev。图12给出不同相遇角旋翼拉力波动的1/2峰峰值。随相遇角增大,1/2峰峰值逐渐降低,旋翼相遇角从0°增加到22.5°时,拉力1/2峰峰值降低了50%。
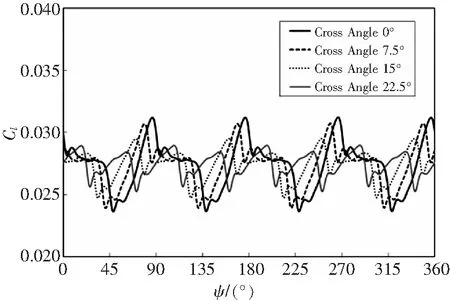
图11 不同相遇角旋翼瞬时拉力系数
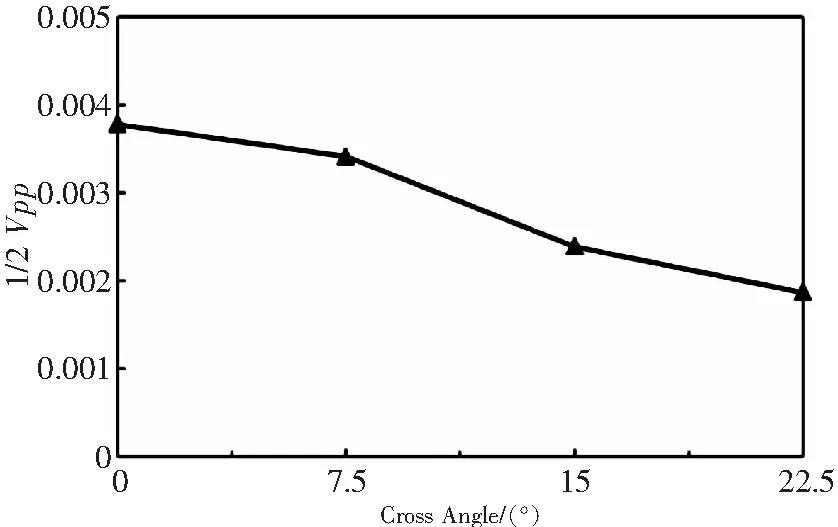
图12 旋翼相遇角对拉力系数1/2峰峰值的影响
图13对不同相遇角共轴刚性旋翼瞬时拉力进行傅里叶变化,以0°相遇角4Ω对应幅值为基准,对各阶幅值进行无因次化。0°相遇角共轴刚性旋翼拉力以4Ω及8Ω的整数倍阶次为主。随着旋翼相遇角增加,4Ω幅值逐渐减小,其他阶次的幅值随之也出现不同程度的下降。当相遇角为22.5°时,旋翼4Ω幅值明显降低,旋翼拉力以8Ω为主。选择合适的旋翼初始方位角可以有效避免旋翼4Ω振动问题,降低旋翼气动载荷。
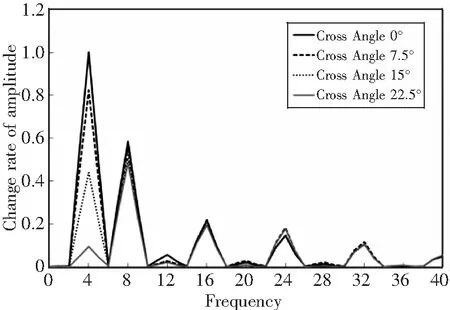
图13 不同旋翼相遇方位角旋翼拉力系数傅里叶变化
图14给出不同前进比下相遇角0°和22.5°的瞬时拉力曲线。速度较小时共轴刚性旋翼周期性相遇的非定常效应起主导作用,旋翼拉力受相遇角的影响较小;随前飞速度增大,旋翼22.5°相遇角较0°相遇角拉力波动明显降低,变化周期从4/Rev变为8/Rev。
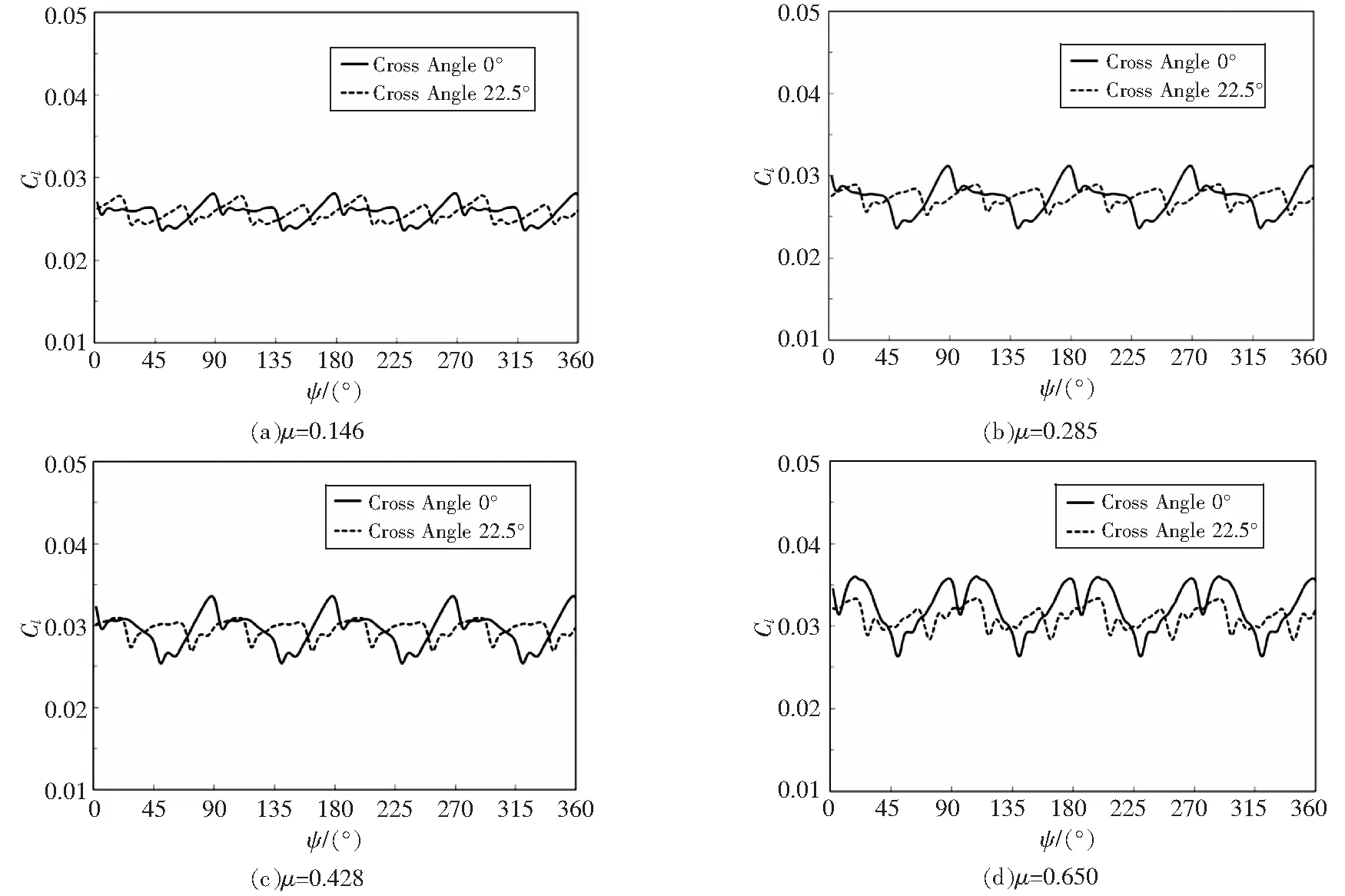
图14 不同前进比旋翼瞬时拉力系数
3 结论
本文基于RANS方程建立了一套适用于共轴刚性旋翼气动干扰特性计算的数值模拟方法,采用运动嵌套网格技术计入旋翼运动,对共轴刚性旋翼悬停和前飞流场进行模拟,并针对旋翼间距、相遇角对旋翼气动干扰特性的影响进行研究,得出以下结论:
1)共轴刚性旋翼悬停流场表现出强烈的非定常气动特性,流场存在严重的桨涡干扰现象,旋翼运动过程中发生“载荷效应”和“厚度效应”,造成旋翼拉力波动;
2)悬停状态,旋翼间距增大,下旋翼对上旋翼的诱导干扰减弱,上旋翼拉力系数和悬停效率逐渐增大,下旋翼则无明显变化;
3)前飞状态旋翼间气动干扰减弱,前行侧桨叶产生大部分升力,后行侧产生升力较小,随前进比增大,旋翼升阻比先增大后减小,升力偏置量增加;
4)旋翼拉力波动随相遇角增大而减小,在中高速度前飞时相遇角22.5°较0°方位角的瞬时拉力曲线1/2峰峰值降低一半,旋翼4Ω幅值明显降低,拉力波动周期从4/Rev变为8/Rev。
