2022年全国新高考Ⅰ卷第7题解法研究
2022-09-22季佳雯李昌成
季佳雯 李昌成
(1.江苏省海门中学 226199;2.新疆乌鲁木齐市第八中学 830002)
比较大小的高考题比比皆是,通常考查指数函数、对数函数、幂函数以及三角函数的大小.一般可以通过函数性质、特殊点、特殊值牵线搭桥,并适度放缩就可以判定大小.但是近两年高考、模考中比较大小的试题风格发生了翻天覆地的变化,难度陡然上升,甚至作为压轴题出现,很多考生见到考题茫然失措.2022年全国新高考Ⅰ卷第7题就是一个典型例子,下面研究它的解法.
1 题目再现

A.a C.c 从a=0.1e0.1,c=-ln0.9看,本题应该是考查利用导数比较大小.但从三个数的形式看,很难发现它们之间的深层次的具体关系,所以我们应打破常规,不能单一考虑某个知识、某个技巧,希望速战速决,这已经不现实.只有综合考虑高中数学的知识,在数据形式上做足文章,还可以联系相关高数知识,多方联合作战也许能突破这个难题. 策略1 以0.1为媒介,联系三个数,作差构造函数. =ln0.1+lne0.1-ln0.1+ln(1-0.1) =0.1+ln(1-0.1), 所以构造函数p(x)=x+ln(1-x),x∈(0,0.1], 故p(x)在(0,0.1] 上单调递减. 可得p(0.1) 即lna-lnb<0.所以a 因为a-c=0.1e0.1+ln0.9=0.1e0.1+ln(1-0.1), 所以构造函数m(x)=xex+ln(1-x),x∈(0,0.1]. 令n(x)=(1-x2)ex-1, 所以n′(x)=(1-x2-2x)ex>0. 所以n(x)在(0,0.1]上单调递增. 即m′(x)>0. 所以m(x)在(0,0.1] 上单调递增. 可得n(x)>n(0)>0. 可得m(0.1)>m(0)=0. 即a-c>0.所以a>c. 故c 评注本解法充分利用了0.1,将其上升为自变量,构造出高中生利用导数能够处理的函数.通过两次作差比较,判定出三者的大小.这是高考中最常见的处理的办法. 解析2 首先研究正数a,b. 所以令h(x)=(1-x)ex.则h′(x)=-xex. 那么h(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减.所以h(x)≤h(0)=1. 所以a 其次研究b,c. 所以构造函数m(x)=ln(1+x)-x(x>0), 于是m(x)在(0,+∞)上单调递减. 所以m(x) 因此b>c. 最后研究a,c.以下同解法1. 评注本解法三次构造函数,过程稍长,但是函数思维符合学生的认知,在解题过程中真实存在.对于自变量的认定,灵活多变,这也是函数的一个特征.对于培养学生的创新意识大有裨益. 策略3 利用教材结论,辅以切线放缩和对数均值关系. 引理1ex>1+x(x≠0). 引理2 lnx≤x-1(x>0),当且仅当x=1时等号成立. 所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减. 于是f(x)≤f(1)=0. 所以lnx≤x-1(x>0),当且仅当x=1时等号成立. 故f(t)在(1,+∞)上单调递减. 所以f(t) 解析3由引理1,得 a=0.1e0.1>0.1(0.1+1)=0.11. 综上c 评注本解法利用了教材习题结论以及教材外的二级结论.我们在教学中要高度重视教材上的习题,这是我们学习的基本要求,也是知识衍生的基础. 策略4 高数助力,用泰勒展开式估算. 对于一些参加过奥赛培训的学生而言,他们知道泰勒展开式可以近似计算一些常见函数值: …… 所以a=0.1e0.1≈0.1×1.105=0.1105. 所以c 评注本解法可以感觉到高等数学视角下的高考题显得那么自然,那么“渺小”.高考要为高校选拔优秀人才,所以有一定的高数基础在考试中受益也是符合人才选拔要求的,也是有利于学生在大学的深造和发展. 高中数学知识点是有限的,但是由有限的知识点发掘出的创新命题点是无限的.只有养成自觉思考、深入研究、善于总结的习惯,才能把握问题的本质,才能提高学生的数学核心素养,才能在高考中展示自己的能力.这类考题有以下几个关键点:一是通过观察、运算、拆分找到数据的链接点(某个常数);二是合理构造函数,函数并不唯一,能解决问题的都是科学的;三是积累一些结论,包括高中教材二级结论、简单高等数学基础等;四是需要坚强的自信心,遇事沉着冷静,培养适应新环境,处理新问题的能力.2 分析题目
3 解法探究
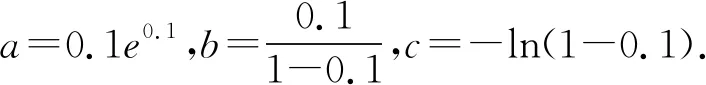
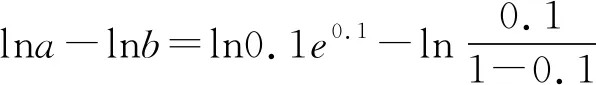

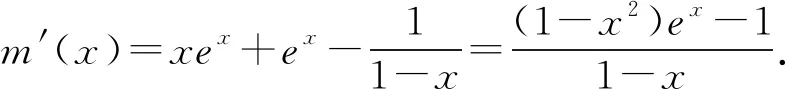




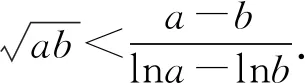

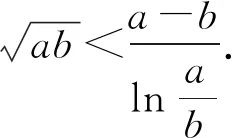
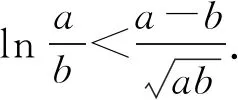
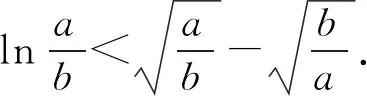
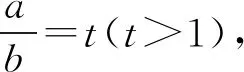
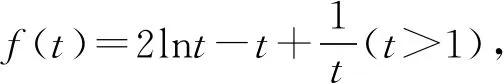
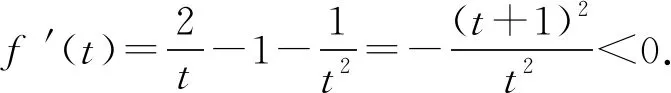
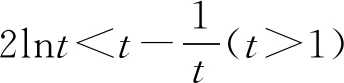
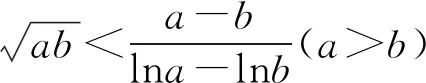
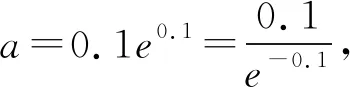

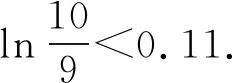

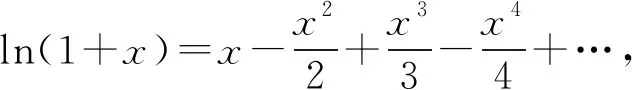
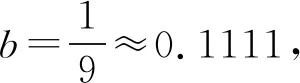
4 解后反思
